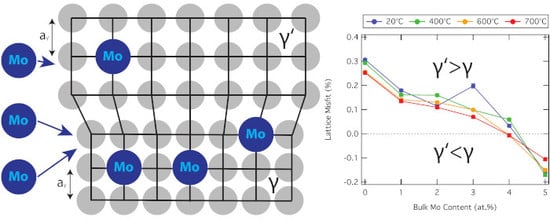
The Effect of Temperature and Mo Content on the Lattice Misfit of Model Ni-Based Superalloys

Abstract

The lattice parameters and misfit of the γ and γ′ phases in a series of model quaternary Ni-based superalloys with and without Mo additions have been determined using neutron diffraction between room temperature and 700 °C. Despite the fact that Mo is typically expected to partition almost exclusively to the γ phase and thereby increase the lattice parameter of that phase alone, the lattice parameters of both the γ and γ′ phases were observed to increase with Mo addition. Nevertheless, the effect on the γ lattice parameter was more pronounced, leading to an overall decrease in the lattice misfit with increasing Mo content. Alloys with the lowest Mo content were found to be positively misfitting, whilst additions of 5 at.% Mo produced a negative lattice misfit. A general decrease in the lattice misfit with increasing temperature was also observed.

1. Introduction

Ni-based superalloys derive their exceptional high temperature strength from the formation of ordered, L1₂ (Strukturbericht notation) γ′ precipitates embedded in a disordered, A1 γ matrix. Due to their similar crystal structures and lattice parameters, the L1₂ precipitates are coherent with the A1 matrix and impart strength through a number of mechanisms, such as order and coherency strengthening [1]. Of these mechanisms, coherency strengthening arises as a result of the different lattice parameters of the γ and γ′ phases, imparting strain into the matrix and thereby inhibiting dislocation motion. Whilst the extent of the strengthening imparted by this mechanism has been debated in the literature [1,2,3,4,5,6,7], it is generally accepted that alloy yield strength increases with larger lattice misfits. The lattice misfit is also known to play a significant role in precipitate coarsening behaviour during service [8,9]. In addition, large negative lattice misfits have been shown to improve creep life [10], whereas smaller lattice misfits have been found to benefit stress rupture life [11]. A full understanding of the link between bulk alloy composition, phase composition and lattice misfit, and how they vary between ambient and service temperature is, therefore, important for the effective optimisation of alloy properties such as yield strength.

A key element in controlling lattice misfit in Ni-based superalloys is Mo. This element preferentially partitions to the γ phase [12], providing solid solution strengthening and increasing the lattice parameter of this phase relative to that of the γ′ phase [13,14,15]. Judicious control of Mo content therefore offers the prospect of tailoring lattice misfit to achieve an appropriate balance between strengthening and precipitate stability. Mo also confers additional benefits that include increased formation of carbides and borides for grain boundary strength [13,16] and improved creep rupture life [11,17]. However, excess Mo is known to promote the formation of Topologically Close Packed phases [10,18], which are considered deleterious to the mechanical properties of these alloys [19].

To better understand the role of Mo on the lattice misfit of Ni-based superalloys, the present study used neutron diffraction to determine the lattice parameters of the γ and γ′ phases, and the resulting lattice misfit, in a series of model superalloys with varying Mo content. Data were acquired between room temperature and 700 °C to deduce the temperature dependence, covering the range of conditions typically encountered in service.

2. Materials and Methods

Alloys with nominal compositions of Ni-14Cr-5Al-5Ti-xMo at.%, where x = 0, 1, 2, 3, 4 and 5 were vacuum arc melted from individual elements of ≥99.9% purity and homogenised at 1250 °C for 22 h in Ar-backfilled glass ampoules. Each alloy was subsequently hot rolled above the γ′ solvus temperature to reduce the grain size. Cylindrical specimens for neutron diffraction of length 8 mm and diameter 5 mm were electro-discharge machined from the hot rolled bars and then aged at 760 °C for 16 h. After each heat treatment, the alloys were air cooled to room temperature.

Samples for microstructural examination were prepared using standard metallographic techniques and characterised using Scanning Electron Microscopy (SEM), on an FEI Nova NanoSEM FEG SEM (FEI, Hillsboro, OR, USA) equipped with an energy dispersive X-ray spectroscopy (EDX) detector. Analyses of the bulk alloy compositions were performed using SEM-EDX on large areas at a range of positions across each sample. Carbon replica samples were produced for analysis using Transmission Electron Microscopy (TEM) (FEI, Hillsboro, OR, USA), full details of which may be found in [20]. Analyses of precipitate size were carried out using Scanning Transmission Electron Microscopy (STEM) on an FEI Tecnai Osiris TEM operated at 200 keV.

Neutron diffraction was carried out at the ISIS Neutron and Muon source, UK, on the ENGIN-X instrument [21]. Samples were mounted in an Instron uniaxial hydraulic loading rig under a load of 50 MPa (minimum load required to hold samples in place) during data acquisition for 20 min at each condition. In addition to room temperature measurements, an optical furnace was used to heat the samples in air to 400, 600 and 700 °C. A K-type thermocouple attached to each sample was used to monitor and control the test temperatures. Full details of the experimental set-up are provided in [22,23]. To determine the lattice parameters of the γ and γ′ phases, the GSAS (General Structure Analysis System) software package (Expgui 1.81, APS, Argonne National Lab, Lemont, IL, USA) [24] was used to fit each diffraction pattern using the Le Bail method [25].

Thermodynamic modelling using ThermoCalc software (version 2017a, ThermoCalc, Solna, Sweden) was carried out to predict the lattice parameters of the model alloys, and to predict the lattice misfit. Equilibrium compositions of the matrix and precipitate phases at the ageing temperature of 760 °C were determined using the TCNi7 database, with all other phases excluded. Maintaining this composition by turning off global minimisation, the predicted molar volumes (V_m) of the γ and γ′ phases were calculated as a function of temperature, thereby enabling determination of the lattice parameters (a) of each phase using;

$$a = {\left[\frac{4V_{\mathrm{m}}}{{\mathrm{N}}_{\mathrm{A}}}\right]}^{1/3}$$

(1)

in which, N_A is Avogadro’s constant. The lattice misfit (δ) was subsequently determined from the lattice parameters of the γ ($a_{\mathsf{\gamma }}$) and γ’ ($a_{{\mathsf{\gamma }}^{\prime }}$) phases using;

$$\delta = \frac{2 \left(a_{{\mathsf{\gamma }}^{\prime }}- a_{\mathsf{\gamma }}\right)}{\left(a_{{\mathsf{\gamma }}^{\prime }}+ a_{\mathsf{\gamma }}\right)}$$

(2)

Global minimisation was turned off to enable the calculation of thermal expansion alone, without additional complications arising from compositional changes with temperature, since these equilibrium predictions are unlikely to be achieved in the short ageing times employed experimentally.

3. Results and Discussion

The compositions of the alloys with varying Mo content, as measured by SEM EDX, are given in

Table 1. Average bulk composition of each of the model alloys, as determined experimentally by SEM EDX.

Alloy (Nominal at.% Mo)	Al	Ti	Cr	Mo	Ni
0	5.42 ± 0.1	5.12 ± 0.06	14.18 ± 0.07	0	75.29 ± 0.1
1	5.19 ± 0.1	4.97 ± 0.08	13.66 ± 0.06	0.73 ± 0.02	75.45 ± 0.07
2	5.54 ± 0.09	5.27 ± 0.04	14.52 ± 0.1	1.72 ± 0.02	72.94 ± 0.1
3	4.99 ± 0.2	5.06 ± 0.05	14.05 ± 0.1	2.58 ± 0.04	73.33 ± 0.1
4	4.85 ± 0.1	4.52 ± 0.1	12.82 ± 0.09	3.13 ± 0.07	74.68 ± 0.2
5	5.24 ± 0.06	5.02 ± 0.05	14.26 ± 0.1	4.48 ± 0.04	71.00 ± 0.1

. All elements were found to be within 1 at.% of their nominal values with the exception of the Cr content of the alloy with a nominal 4 at.% Mo. The low uncertainties associated with the bulk alloy compositions indicate that the homogenisation heat treatment was successful and each sample is effectively homogeneous with regards to chemical composition.

Figure 1 shows characteristic intragranular STEM images of each alloy. It is evident that most of the alloys possessed a unimodal precipitate size distribution, with the exception of the 0 and 2 at.% Mo alloys, which were bimodal with larger secondary and smaller tertiary γ′ (Figure 1a,c respectively). As the material was heat treated in the single-phase field, no primary γ′ was present on the grain boundaries of any alloy.

In all alloys, with the exception of the 1 at.% Mo alloy, the secondary γ′ precipitates were of similar size (

Table 2. Average precipitate diameters of the secondary and tertiary γ′ in each alloy of the series.

Alloy (Nominal at.% Mo)	Diameter of Secondary γ′ (nm)	Diameter of Tertiary γ′ (nm)
0	76 ± 14	20 ± 5
1	41 ± 8	-
2	92 ± 18	12 ± 3
3	89 ± 16	-
4	85 ± 11	-
5	105 ± 18	-

) within the confines of experimental uncertainty. These precipitates were larger than the size associated with the transition from weak to strong pair dislocation coupling [1,26,27] and are typical of those reported in commercial polycrystalline Ni-based superalloys [28,29,30,31,32]. The reasons for the occurrence of tertiary γ′ precipitates in the 0 and 2 at.% Mo alloys are unclear and may be attributed to a range of factors including variations in the cooling rates experienced by the alloys, differential alloy response to the metallographic techniques used to prepare the carbon replica samples, and compositional sensitivities of the individual alloys. However, since the volume fractions of the tertiary γ′ are significantly smaller than those of the secondary γ′ (as seen in Figure 1), the neutron diffraction data would be dominated by the contribution of the secondary γ′.

The diffraction patterns from all alloys contained peaks consistent with the presence of γ and γ′ phases only. In addition, in all cases the similarity of the lattice parameters of the γ and γ′ phases resulted in overlapping fundamental reflections. However, performing full-pattern Le Bail refinements of the data permitted determination of the lattice parameters of the two phases. An example of a fitted diffraction pattern obtained from the 2 at.% Mo alloy at 700 °C is shown in Figure 2.

Ni-based superalloys often contain multi-modal precipitate size distributions that differ in average composition [33]. Although this compositional variation would be expected to result in differing diffraction peak positions, due to the very similar lattice parameters of these distributions and that of the matrix itself, diffraction peaks from individual precipitate size distributions cannot normally be distinguished. Additionally, as previously noted, the volume fraction of secondary γ′ is much larger than that of the tertiary γ′ and therefore the contribution of the tertiary γ′ to the overall peak intensity is expected to be small.

Asymmetries were observed in some of the diffraction peaks, most notably the (200) from the 0 and 1 at.% Mo alloys, which occurred at lower d-spacings than the main peak. These asymmetries may be attributed to a stress-induced tetragonal distortion of the matrix caused by the presence of the precipitates. This effect would be expected to be most apparent in the (200) reflection and in alloys with the largest lattice misfits, consistent with the observations made.

It is noted that the Le Bail method inherently allows arbitrary scaling of diffraction peak intensities. As such, fitting diffraction data with closely overlapping peaks may result in the fitted peaks being dominated by the contribution of a single phase. Evidence of this was observed in the fits to the fundamental reflections from the alloys with 3 and 4 at.% Mo, consistent with them having lower lattice misfits and hence more closely spaced peaks. To ensure that the lattice parameters obtained were not adversely affected by Le Bail fitting, additional analyses were performed using single peak fitting, the details of which are provided in the Supplementary Information (see Figure S1). These analyses confirmed that the lattice parameters and misfits obtained using the Le Bail method were sufficiently representative and not adversely compromised by arbitrary scaling of peak intensity.

The predicted and experimental lattice parameters of the model alloys are shown in Figure 3 as a function of bulk Mo content, at varying temperatures between 20 °C and 700 °C. Both the predicted and experimental values suggest an increase in the lattice parameters for both phases with bulk Mo content, although the rate of increase in lattice parameter varies between the two phases in the predicted and experimental data. Most significantly, the rate of increase in the predicted γ′ lattice parameter with Mo content is lower than that of the γ phase, since at equilibrium Mo is expected to partition almost exclusively to the γ phase [10,12,13]. However, previous work has shown that this may not be the case, with high Mo contents found in the γ′ precipitates [15], particularly in the tertiary γ′ [34]. This has been attributed to the fact that short ageing times or fast cooling rates may not allow thermodynamic equilibrium to be achieved, resulting in non-equilibrium compositions. The experimentally determined compositions of the γ′ precipitates in this model quaternary alloy series with and without Mo additions were reported in previous studies [20,34]. Notably, high Mo and Cr contents were observed in the tertiary γ′, for example, approximately 4 at.% Mo was measured in the tertiary γ′ of the 5 at.% Mo alloy, despite almost zero Mo being predicted in this phase by ThermoCalc. The experimentally determined Mo contents of the secondary γ′ were also greater than those predicted by ThermoCalc, although the extent of which was lower than that of the tertiary γ′.

Increasing temperature was also predicted by ThermoCalc to increase the lattice parameters of both phases, but to a larger extent in the matrix phase. This occurs as a result of the different thermal expansion coefficients of the γ and γ′ phases, with the lattice parameter of the disordered γ matrix phase increasing faster with temperature than that of the ordered γ′ phase [35]. A similar trend was observed with the experimental data. However, the absolute values of the lattice parameters differed between prediction and experiment, with the lattice parameters of the two phases being more similar in the experimental data. This disparity may be partially attributed to the fact that ThermoCalc predicts the unconstrained lattice parameters, whereas experimentally the two phases are naturally constrained to be closer in lattice parameter. Therefore, ThermoCalc predictions were not expected to quantitatively match experiment, although they still provided a useful comparison to the qualitative trends [9].

The predicted and experimentally determined lattice misfits of each alloy are shown in Figure 4. Both sets of data indicate that the lattice misfit decreases with increasing Mo content. This arises as a result of the more significant increase in the lattice parameter of the γ phase with Mo content. At room temperature, the lattice misfit was predicted to be positive for all Mo contents, whilst the experimental data identified a transition from positive to negative lattice misfits above 4 at.% Mo. For many of the alloys, the experimentally determined lattice misfits become more negative with increasing temperature, consistent with the trend observed in the predicted values. Interestingly, the 4 at.% Mo alloy, which had the smallest lattice misfit, showed a transition from positive to negative lattice misfit between 400 and 600 °C.

However, whilst the trends in the predicted and experimental data were similar, the magnitudes differed significantly. This may arise as a result of a number of factors including the non-equilibrium compositions of the γ’ precipitates in the experimental alloys and the effect of lattice constraint. In the previous studies that have determined the γ′ compositions in these alloys [20,34], a high Mo content was reported, which would result in a larger lattice parameter than that expected from equilibrium. This would give rise to a larger lattice misfit in positively misfitting alloys and a smaller lattice misfit in negatively misfitting alloys. This is not readily apparent in the present results (Figure 4) and, as such, it must be concluded that the difference in constrained and unconstrained lattice parameters outweigh the compositional effect.

The lattice parameters of the γ and γ’ phases have also been shown to be sensitive to time at temperature and cooling rate, with slower cooling rates resulting in reduced sphericity of secondary γ′ precipitates and increased unconstrained lattice misfit. This was caused by a γ′ composition that is further from equilibrium [36,37]. Interestingly, in these studies, the constrained lattice misfit was only seen to vary slightly with cooling rate due to the formation of complex γ′ morphologies with associated compressive strains. A separate study has found that increased ageing time resulted in increased γ′ size and increased lattice misfit, whilst a two-stage heat treatment resulted in more complex γ′ morphologies and associated lattice misfit dependence [38]. It was concluded that these effects arise due to compositional variations, with faster cooling rates or shorter ageing times resulting in γ′ precipitates with compositions further from the predicted equilibrium. In the present alloy series, this effect means that large atoms such as Mo do not have time to diffuse to the γ phase during the comparatively short duration heat treatments applied. The γ′ precipitate phase therefore has a higher Mo content, and larger lattice parameter, as Mo has a large atomic radius.

The γ′ precipitates in the alloys with low Mo contents were approximately spherical and became progressively more cuboidal as the bulk Mo content was increased (Figure 1). This observation is inconsistent with previous studies which have shown that the morphology of γ′ is linked to the precipitate size and the lattice misfit [8], with the sphere-cuboid transition expected to occur at lower ageing times in alloys with higher lattice misfits.

It is generally considered desirable for commercial alloys to have a lattice misfit which is as close to zero as possible, to minimise coarsening at the high temperatures experienced during operation. Based on this argument, the 4 at.% Mo alloy may be expected to show the greatest precipitate coarsening resistance at high temperatures. However, precipitate ageing studies on this alloy series have proved inconclusive with limited coarsening behaviour evident for all alloys outside of experimental uncertainty. However, the effect of Mo content on lattice misfit alone cannot be used in isolation for alloy design, since other factors, e.g., the propensity for Topologically Closed Packed phase formation must be taken into account.

4. Conclusions

The lattice parameters and lattice misfit of a model series of quaternary Ni-based superalloys with and without Mo additions have been determined experimentally and compared to equilibrium predictions. It was found that increasing bulk Mo content and increasing temperature led to larger lattice parameters of both the γ and γ′ phases, even though Mo is expected to partition almost exclusively to the matrix phase. The lattice misfit was found to decrease with Mo content, being positive for low Mo contents, negative for the highest Mo contents, and passing through zero at the 4 at.% Mo alloy. Increased temperature generally decreased the lattice misfit, thereby reducing the lattice misfit of the positively misfitting alloys whilst increasing the magnitude of the lattice misfit of the negatively misfitting alloy. These data have important consequences on alloy design, where a minimal lattice misfit may be desired at operating temperatures.