Stochastic Analysis of Tsunami Hazard of the 1945 Makran Subduction Zone Mw 8.1–8.3 Earthquakes
Abstract
:1. Introduction
2. Methodology
2.1. Tsunami Source
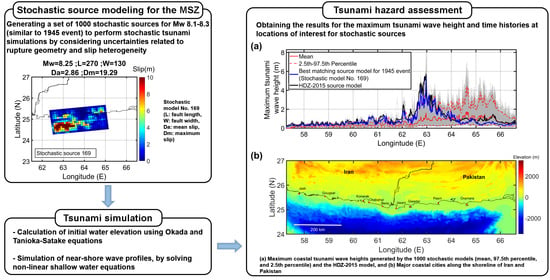
2.1.1. Makran Fault Model
2.1.2. Earthquake Source Parameters for the Makran Region
2.2. Bathymetry and Elevation Data
2.3. Tsunami Simulation
2.4. Stochastic Tsunami Simulation
2.5. Observations
3. Results
3.1. Stochastic Slip Models
3.2. Comparison with Observations
3.3. Effect of Earthquake Slip and Fault Geometry on Tsunami Simulation Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tomotsuka, T.; Kazumasa, K.; Fumihiko, I.; Yoshiaki, K.; Susumu, M.; Shigeo, T. Tsunami: To Survive from Tsunami; World Scientific: Singapore, 2018; Volume 46, ISBN 9813239409. [Google Scholar]
- Kajitani, Y.; Chang, S.E.; Tatano, H. Economic Impacts of the 2011 Tohoku-Oki Earthquake and Tsunami. Earthq. Spectra 2013, 29, 457–478. [Google Scholar] [CrossRef]
- Fraser, S.A.; Raby, A.C.; Pomonis, A.; Goda, K.; Chian, S.C.; Macabuag, J.; Offord, M.; Saito, K.; Sammonds, P. Tsunami damage to coastal defences and buildings in the March 11th 2011 M w 9.0 Great East Japan earthquake and tsunami. Bull. Earthq. Eng. 2012, 11, 205–239. [Google Scholar] [CrossRef]
- Synolakis, C.E.; Bernard, E.N. Tsunami science before and beyond Boxing Day 2004. Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 2006, 364, 2231–2265. [Google Scholar] [CrossRef]
- Byrne, D.E.; Sykes, L.R.; Davis, D.M. Great thrust earthquakes and aseismic slip along the plate boundary of the Makran Subduction Zone. J. Geophys. Res. Space Phys. 1992, 97, 449–478. [Google Scholar] [CrossRef]
- ArrayExpress—A Database of Functional Genomics Experiments. Available online: http://www.ebi.ac.uk/arrayexpress/ (accessed on 12 November 2012).
- Duda, S.J. Secular seismic energy release in the circum-Pacific belt. Tectonophysics 1965, 2, 409–452. [Google Scholar] [CrossRef]
- Page, W.D.; Alt, J.N.; Cluff, L.S.; Plafker, G. Evidence for the recurrence of large-magnitude earthquakes along the Makran coast of Iran and Pakistan. Tectonophysics 1979, 52, 533–547. [Google Scholar] [CrossRef]
- Heck, N.H. List of seismic sea waves. Bull. Seismol. Soc. Am. 1947, 37, 269–286. [Google Scholar]
- Heidarzadeh, M.; Pirooz, M.D.; Zaker, N.H.; Yalciner, A.C. Preliminary estimation of the tsunami hazards associated with the Makran subduction zone at the northwestern Indian Ocean. Nat. Hazards 2008, 48, 229–243. [Google Scholar] [CrossRef]
- Neetu, S.; Suresh, I.; Shankar, R.; Nagarajan, B.; Sharma, R.; Shenoi, S.S.C.; Unnikrishnan, A.S.; Sundar, D. Trapped waves of the 27 November 1945 Makran tsunami: Observations and numerical modeling. Nat. Hazards 2011, 59, 1609–1618. [Google Scholar] [CrossRef]
- Heidarzadeh, M.; Satake, K. New Insights into the Source of the Makran Tsunami of 27 November 1945 from Tsunami Waveforms and Coastal Deformation Data. Pure Appl. Geophys. 2014, 172, 621–640. [Google Scholar] [CrossRef]
- Heidarzadeh, M.; Satake, K. A Combined Earthquake–Landslide Source Model for the Tsunami from the 27 November 1945 M w 8.1 Makran Earthquake. Bull. Seismol. Soc. Am. 2017, 107, 1033–1040. [Google Scholar] [CrossRef] [Green Version]
- Jaiswal, R.K.; Singh, A.P.; Rastogi, B.K. Simulation of the Arabian Sea Tsunami propagation generated due to 1945 Makran Earthquake and its effect on western parts of Gujarat (India). Nat. Hazards 2008, 48, 245–258. [Google Scholar] [CrossRef]
- Heidarzadeh, M.; Pirooz, M.D.; Zaker, N.H.; Synolakis, C.E. Evaluating Tsunami Hazard in the Northwestern Indian Ocean. Pure Appl. Geophys. 2008, 165, 2045–2058. [Google Scholar] [CrossRef]
- Mai, P.M.; Beroza, G.C. A spatial random field model to characterize complexity in earthquake slip. J. Geophys. Res. Space Phys. 2002, 107, ESE 10-1–ESE 10-21. [Google Scholar] [CrossRef]
- Fukutani, Y.; Suppasri, A.; Imamura, F. Stochastic analysis and uncertainty assessment of tsunami wave height using a random source parameter model that targets a Tohoku-type earthquake fault. Stoch. Environ. Res. Risk Assess. 2014, 29, 1763–1779. [Google Scholar] [CrossRef] [Green Version]
- Woessner, J.; Farahani, R.J. Tsunami inundation hazard across Japan. Int. J. Disaster Risk Reduct. 2020, 49, 101654. [Google Scholar] [CrossRef]
- Mori, N.; Muhammad, A.; Goda, K.; Yasuda, T.; Ruiz-Angulo, A. Probabilistic Tsunami Hazard Analysis of the Pacific Coast of Mexico: Case Study Based on the 1995 Colima Earthquake Tsunami. Front. Built Environ. 2017, 3, 34. [Google Scholar] [CrossRef]
- Muhammad, A.; Goda, K.; Alexander, N.A. Tsunami Hazard Analysis of Future Megathrust Sumatra Earthquakes in Padang, Indonesia Using Stochastic Tsunami Simulation. Front. Built Environ. 2016, 2, 33. [Google Scholar] [CrossRef] [Green Version]
- González, J.; González, G.; Aránguiz, R.; Melgar, D.; Zamora, N.; Shrivastava, M.N.; Das, R.; Catalán, P.A.; Cienfuegos, R. A hybrid deterministic and stochastic approach for tsunami hazard assessment in Iquique, Chile. Nat. Hazards 2019, 100, 231–254. [Google Scholar] [CrossRef]
- Rashidi, A.; Shomali, Z.H.; Dutykh, D.; Farajkhah, N.K. Tsunami hazard assessment in the Makran subduction zone. Nat. Hazards 2020, 100, 861–875. [Google Scholar] [CrossRef] [Green Version]
- Goda, K.; Yasuda, T.; Mori, N.; Maruyama, T. New Scaling Relationships of Earthquake Source Parameters for Stochastic Tsunami Simulation. Coast. Eng. J. 2016, 58, 1650010. [Google Scholar] [CrossRef] [Green Version]
- Hayes, G.P.; Moore, G.L.; Portner, D.E.; Hearne, M.; Flamme, H.; Furtney, M.; Smoczyk, G.M. Slab2, a comprehensive subduction zone geometry model. Science 2018, 362, 58–61. [Google Scholar] [CrossRef] [PubMed]
- Smith, G.L.; McNeill, L.C.; Wang, K.; He, J.; Henstock, T.J. Thermal structure and megathrust seismogenic potential of the Makran subduction zone. Geophys. Res. Lett. 2013, 40, 1528–1533. [Google Scholar] [CrossRef] [Green Version]
- Bird, P. An updated digital model of plate boundaries. Geochem. Geophys. Geosystems 2003, 4, 4. [Google Scholar] [CrossRef]
- Müller, R.D.; Roest, W.R.; Royer, J.-Y.; Gahagan, L.M.; Sclater, J.G. Digital isochrons of the world’s ocean floor. J. Geophys. Res. Space Phys. 1997, 102, 3211–3214. [Google Scholar] [CrossRef]
- Gudmundsson, Ó.; Sambridge, M. A regionalized upper mantle (RUM) seismic model. J. Geophys. Res. Space Phys. 1998, 103, 7121–7136. [Google Scholar] [CrossRef]
- Syracuse, E.M.; Abers, G.A. Global compilation of variations in slab depth beneath arc volcanoes and implications. Geochem. Geophys. Geosystems 2006, 7, 7. [Google Scholar] [CrossRef]
- Hayes, G.P.; Wald, D.J.; Johnson, R.L. Slab1.0: A three-dimensional model of global subduction zone geometries. J. Geophys. Res. Space Phys. 2012, 117, 117. [Google Scholar] [CrossRef]
- Penney, C.; Tavakoli, F.; Saadat, A.; Nankali, H.R.; Sedighi, M.; Khorrami, F.; Sobouti, F.; Rafi, Z.; Copley, A.; Jackson, J.; et al. Megathrust and accretionary wedge properties and behaviour in the Makran subduction zone. Geophys. J. Int. 2017, 209, 1800–1830. [Google Scholar] [CrossRef]
- Mai, P.M.; Thingbaijam, K.K.S. SRCMOD: An Online Database of Finite-Fault Rupture Models. Seism. Res. Lett. 2014, 85, 1348–1357. [Google Scholar] [CrossRef]
- GEBCO. The GEBCO_2019 Grid: A Continuous Terrain Model of the Global Oceans and Land. Available online: https://www.gebco.net/data_and_products/gridded_bathymetry_data/gebco_2019/gebco_2019_info.html (accessed on 9 October 2020).
- USGS. Shuttle Radar Topography Mission (SRTM) 1 Arc-Second Global; U.S. Geological Survey: Reston, VA, USA, 2015.
- Goto, C.; Ogawa, Y.; Shuto, N.; Imamura, F. Numerical Method of Tsunami Simulation with the Leap-Frog Scheme; Intergovernmental Oceanographic Commission of UNESCO: Paris, France, 1997; Volume 35, p. 126. [Google Scholar]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Tanioka, Y.; Satake, K. Tsunami generation by horizontal displacement of ocean bottom. Geophys. Res. Lett. 1996, 23, 861–864. [Google Scholar] [CrossRef] [Green Version]
- Goda, K.; Song, J. Uncertainty modeling and visualization for tsunami hazard and risk mapping: A case study for the 2011 Tohoku earthquake. Stoch. Environ. Res. Risk Assess. 2015, 30, 2271–2285. [Google Scholar] [CrossRef] [Green Version]
- Bell, C.; Vassie, J.M.; Woodworth, P.L. POL/PSMSL Tidal Analysis Software Kit 2000 (TASK-2000); Permanent Service for Mean Sea Level, CCMS Proudman Oceanographic Laboratory, Bidston Observatory: Birkenhead, UK, 1999; Volume 20, pp. 32–46. [Google Scholar]
- Ambraseys, N.; Melville, C.P. A History of Persian Earthquakes; Cambridge University Press: New York, NY, USA, 1982. [Google Scholar]
- De Risi, R.; Goda, K. Simulation-Based Probabilistic Tsunami Hazard Analysis: Empirical and Robust Hazard Predictions. Pure Appl. Geophys. 2017, 174, 3083–3106. [Google Scholar] [CrossRef] [Green Version]












| Top 20 Sources for Mumbai | Ranking of the Selected Sources | ||
|---|---|---|---|
| Ranking | Source No. | For Karachi | For Ormara |
| 1 | 659 | 73 | 241 |
| 2 | 937 | 787 | 331 |
| 3 | 84 | 847 | 356 |
| 4 | 169 | 92 | 10 |
| 5 | 730 | 177 | 533 |
| 6 | 883 | 848 | 274 |
| 7 | 418 | 815 | 324 |
| 8 | 479 | 203 | 844 |
| 9 | 230 | 94 | 528 |
| 10 | 363 | 882 | 341 |
| 11 | 930 | 976 | 333 |
| 12 | 910 | 801 | 785 |
| 13 | 792 | 494 | 901 |
| 14 | 403 | 35 | 244 |
| 15 | 349 | 908 | 970 |
| 16 | 698 | 164 | 743 |
| 17 | 842 | 303 | 890 |
| 18 | 941 | 972 | 301 |
| 19 | 610 | 940 | 245 |
| 20 | 375 | 563 | 261 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Momeni, P.; Goda, K.; Heidarzadeh, M.; Qin, J. Stochastic Analysis of Tsunami Hazard of the 1945 Makran Subduction Zone Mw 8.1–8.3 Earthquakes. Geosciences 2020, 10, 452. https://doi.org/10.3390/geosciences10110452
Momeni P, Goda K, Heidarzadeh M, Qin J. Stochastic Analysis of Tsunami Hazard of the 1945 Makran Subduction Zone Mw 8.1–8.3 Earthquakes. Geosciences. 2020; 10(11):452. https://doi.org/10.3390/geosciences10110452
Chicago/Turabian StyleMomeni, Payam, Katsuichiro Goda, Mohammad Heidarzadeh, and Jinhui Qin. 2020. "Stochastic Analysis of Tsunami Hazard of the 1945 Makran Subduction Zone Mw 8.1–8.3 Earthquakes" Geosciences 10, no. 11: 452. https://doi.org/10.3390/geosciences10110452
APA StyleMomeni, P., Goda, K., Heidarzadeh, M., & Qin, J. (2020). Stochastic Analysis of Tsunami Hazard of the 1945 Makran Subduction Zone Mw 8.1–8.3 Earthquakes. Geosciences, 10(11), 452. https://doi.org/10.3390/geosciences10110452