The Noise Properties and Velocities from a Time-Series of Estonian Permanent GNSS Stations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Calculation of cGNSS Stations Coordinates
2.2. Time-Series Analysis
2.3. Noise Analysis
- white noise (WN);
- generalized Gauss–Markov noise (GGM);
- generalized Gauss–Markov noise + white noise (GGM + WN);
- power law noise + white noise (PLN + WN);
- flicker noise + white noise (FN + WN);
- flicker noise + random walk (FN + RW).
3. Results and Discussion
3.1. Outliers Removal
- GOA, outliers removed with Tsview and 3-sigma level (solution GOA_1);
- GOA, outliers removed with Hector and IQ-factor 2.2 (solution GOA_2);
- GOA, outliers removed with Hector and IQ-factor 3 (solution GOA_3);
- BERN, outliers removed with Tsview and 3-sigma level (solution BERN_1);
- BERN, outliers removed with Hector and IQ-factor 2.2 (solution BERN_2);
- BERN, outliers removed with Hector and IQ-factor 3 (solution BERN_3).
3.2. Noise Properties
3.3. Time-Series Analysis
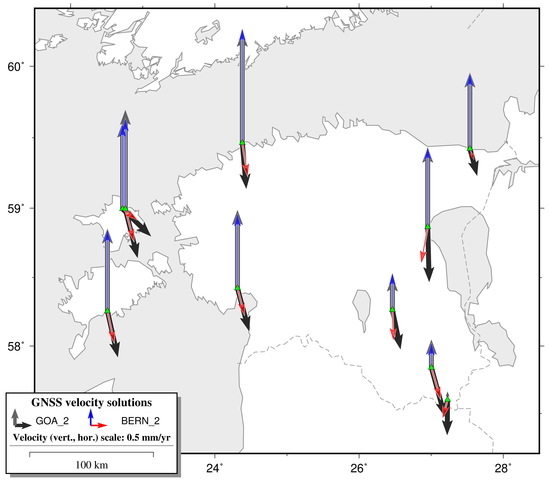
3.4. Comparison and Validation of the Velocity Estimates
3.4.1. Gipsy–Oasis Time-Series and Hector Solution
3.4.2. Bernese Time-Series and Hector Solution
3.4.3. MIDAS Solution
3.4.4. Tsview Solution
3.5. Comparison of Different Softwares
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jevrejeva, S.; Rudja, A.; Makinen, J. Postglacial rebound in Fennoscandia: New results from Estonian tide gauges. In Gravity Geoid and Geodynamics 2000; Sideris, M.G., Ed.; Springer: Berlin, Germany, 2002; Volume 123, pp. 193–198. [Google Scholar]
- Kall, T.; Oja, T.; Tänavsuu, K. Postglacial land uplift in Estonia based on four precise levelings. Tectonophysics 2014, 610, 25–38. [Google Scholar] [CrossRef]
- Suursaar, Ü.; Kall, T. Decomposition of Relative Sea Level Variations at Tide Gauges Using Results from Four Estonian Precise Levelings and Uplift Models. IEEE J. Select. Top. Appl. Earth Observ. Remote Sens. 2018, 1–9. [Google Scholar] [CrossRef]
- Vallner, L.; Sildvee, H.; Torim, A. Recent Crustal Movements in Estonia. J. Geodyn. 1988, 9, 215–223. [Google Scholar] [CrossRef]
- Yakubovski, O. Renewed Map of Vertical Movements of the Earth’s Crust on the Coasts of the Baltic Sea. In Proceedings of the Recent Crustal Movements; Academy of Sciences of the Estonian SSR: Tallinn, Estonia, 1973; Volume 5, pp. 72–78. [Google Scholar]
- Oja, T.; Kollo, K.; Pihlak, P. GIAst ja maapinna liikumistest Eestis GNSS täppismõõtmiste valguses/About GIA and Earth’s surface movements in Estonia in light of the precise GNSS measurements. Geodeet 2014, 44, 55–65. [Google Scholar]
- Kierulf, H.P.; Steffen, H.; Simpson, M.J.R.; Lidberg, M.; Wu, P.; Wang, H. A GPS velocity field for Fennoscandia and a consistent comparison to glacial isostatic adjustment models. J. Geophys. Res. B Solid Earth 2014, 119, 6613–6629. [Google Scholar] [CrossRef] [Green Version]
- Lidberg, M.; Johansson, J.M.; Scherneck, H.-G.; Milne, G.A. Recent results based on continuous GPS observations of the GIA process in Fennoscandia from BIFROST. J. Geodyn. 2010, 50, 8–18. [Google Scholar] [CrossRef] [Green Version]
- Scherneck, H.; Johansson, J.M.; Elgered, G.; Davis, J.L.; Jonsson, B.; Hedling, G.; Koivula, H.; Ollikainen, M.; Poutanen, M.; Vermeer, M. Bifrost: Observing the Three-Dimensional Deformation of Fennoscandia. Ice Sheets Sea Level Dyn. Earth 2002, 69–93. [Google Scholar] [CrossRef]
- Vestøl, O.; Ågren, J.; Steffen, H.; Kierulf, H.; Lidberg, M.; Oja, T.; Rüdja, A.; Kall, T.; Saaranen, V.; Engsager, K.; et al. NKG2016LU, An Improved Postglacial Land Uplift Model over the Nordic-Baltic Region. Available online: https://www.lantmateriet.se/contentassets/58490c18f7b042e5aa4c38075c9d3af5/presentation-av-nkg2016lu.pdf (accessed on 13 May 2019).
- Lahtinen, S.; Pasi, H.; Jivall, L.; Kempe, C.; Kollo, K.; Kosenko, K.; Pihlak, P.; Prizginiene, D.; Tangen, O.; Weber, M. First results of the Nordic and Baltic GNSS Analysis Centre. J. Geod. Sci. 2018, 8, 34–42. [Google Scholar] [CrossRef]
- Jagoda, M. Influence of use of different values of tidal parameters h2, l2 on determination of coordinates of SLR stations. Stud. Geophys. Geod. 2019, 63, 71–82. [Google Scholar] [CrossRef]
- Guo, J.; Wang, Y.; Shen, Y.; Liu, X.; Sun, Y.; Kong, Q. Estimation of SLR station coordinates by means of SLR measurements to kinematic orbit of LEO satellites. Earth Planets Space 2018, 70, 201. [Google Scholar] [CrossRef] [Green Version]
- Saunier, J.; Auriol, A.; Tourain, C. Initiating an error budget of the DORIS ground antenna position: Genesis of the Starec antenna type C. Adv. Space Res. 2016, 58, 2717–2724. [Google Scholar] [CrossRef]
- De Zeeuw-van Dalfsen, E.; Sleeman, R. A Permanent, Real-Time Monitoring Network for the Volcanoes Mount Scenery and The Quill in the Caribbean Netherlands. Geosciences 2018, 8, 320. [Google Scholar] [CrossRef]
- Crétaux, J.-F.; Soudarin, L.; Davidson, F.J.M.; Gennero, M.-C.; Bergé-Nguyen, M.; Cazenave, A. Seasonal and interannual geocenter motion from SLR and DORIS measurements: Comparison with surface loading data. J. Geophys. Res. Solid Earth 2002, 107, ETG 16-1–ETG 16-9. [Google Scholar] [CrossRef]
- Cigna, F. Observing Geohazards from Space. Geosciences 2018, 8, 59. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
- Williams, S.D.P. The effect of coloured noise on the uncertainties of rates estimated from geodetic time-series. J. Geod. 2003, 76, 483–494. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Bouin, M.-N.; Collilieux, X.; Wöppelmann, G. Correlated errors in GPS position time-series: Implications for velocity estimates. J. Geophys. Res. Solid Earth 2011, 116. [Google Scholar] [CrossRef]
- He, X.; Montillet, J.-P.; Fernandes, R.; Bos, M.; Yu, K.; Hua, X.; Jiang, W. Review of current GPS methodologies for producing accurate time-series and their error sources. J. Geodyn. 2017, 106, 12–29. [Google Scholar] [CrossRef]
- Mao, A.; Harrison, C.G.; Dixon, T.H. Noise in GPS coordinate time-series. J. Geophys. Res. Solid Earth 1999, 104, 2797–2816. [Google Scholar] [CrossRef]
- Williams, S.D.P.; Bock, Y.; Fang, P.; Jamason, P.; Nikolaidis, R.M.; Prawirodirdjo, L.; Miller, M.; Johnson, D.J. Error analysis of continuous GPS position time-series. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, B.; Wang, Q.; Yang, S. Noise analysis of continuous GPS coordinate time-series for CMONOC. Adv. Space Res. 2012, 49, 943–956. [Google Scholar] [CrossRef]
- Goudarzi, M.A.; Cocard, M.; Santerre, R. Noise behavior in CGPS position time-series: The eastern North America case study. J. Geod. Sci. 2015, 5. [Google Scholar] [CrossRef]
- Langbein, J. Noise in GPS displacement measurements from Southern California and Southern Nevada. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Herring, T. MATLAB Tools for viewing GPS velocities and time-series. GPS Solut. 2003, 7, 194–199. [Google Scholar] [CrossRef]
- Langbein, J. Noise in two-color electronic distance meter measurements revisited. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Williams, S.D.P. CATS: GPS coordinate time-series analysis software. GPS Solut. 2008, 12, 147–153. [Google Scholar] [CrossRef]
- Herring, T.A.; King, R.W.; McClusky, S.C. Introduction to Gamit/Globk; Massachusetts Institute of Technology: Cambridge, MA, USA; Available online: http://www-gpsg.mit.edu/~simon/gtgk/Intro_GG.pdf (accessed on 13 May 2019).
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast error analysis of continuous GNSS observations with missing data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2; University of Bern, Bern Open Publishing: Bern, Switzerland, 2015. [Google Scholar]
- Blewitt, G.; Kreemer, C.; Hammond, W.C.; Gazeaux, J. MIDAS robust trend estimator for accurate GPS station velocities without step detection. J. Geophys. Res. Solid Earth 2016, 121, 2054–2068. [Google Scholar] [CrossRef]
- Kaniuth, K.; Völksen, C. Comparison of the BERNESE and GIPSY/OASIS II software systems using EUREF data. J. Mitt Bundesamtes Kartographie Geodasie 2003, 29, 314–319. [Google Scholar]
- Drewes, H.; Kaniuth, K.; Costa, S.A.; Fortes, L.S. Results of the SIRGAS Campaign 2000 and Coordinates Variations with Respect to the 1995. In A Window on the Future of Geodesy: Proceedings of the International Association of Geodesy. IAG General Assembly, Sapporo, Japan, 30 June–11 July 11, 2003; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Khan, S.A.; Knudsen, P. Comparison between GIPSY OASIS 6.0 and BERNESE 5.0 Time-Series for Long Term GPS Stations in Denmark. EUREF Publication. 2012. Available online: http://www.euref.eu/symposia/2011Chisinau/P-03-p-Khan.pdf (accessed on 13 May 2019).
- Kollo, K.; Kall, T.; Liibusk, A. Computation of Estonian CORS data using Bernese 5.2 and Gipsy 6.4 softwares. In Proceedings of the EGU General Assembly Conference Abstracts; Copernicus: Vienna, Austria, 2017; Volume 19, p. 609. [Google Scholar]
- He, Y.; Zhang, S.; Wang, Q.; Liu, Q.; Qu, W.; Hou, X. HECTOR for Analysis of GPS Time-series. In Proceedings of the China Satellite Navigation Conference; Springer: Singapore, 2018; pp. 187–196. [Google Scholar]
- Langbein, J. Improved efficiency of maximum likelihood analysis of time-series with temporally correlated errors. J. Geod. 2017, 91, 985–994. [Google Scholar] [CrossRef]
- Ågren, J.; Svensson, R. Postglacial Land Uplift Model and System Definition for the New Swedish Height System RH 2000. Lantmäteriet, 2007. Available online: https://www.lantmateriet.se/contentassets/4a728c7e9f0145569edd5eb81fececa7/lmv-rapport_2007_4.pdf (accessed on 13 May 2019).
- Simon, K.M.; Riva, R.E.M.; Kleinherenbrink, M.; Frederikse, T. The glacial isostatic adjustment signal at present day in northern Europe and the British Isles estimated from geodetic observations and geophysical models. Solid Earth 2018, 9, 777–795. [Google Scholar] [CrossRef] [Green Version]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. J. Geophys. Res. Solid Earth 2015, 120, 450–487. [Google Scholar] [CrossRef]
- Metsar, J.; Kollo, K.; Ellmann, A. Modernization of the Estonian National GNSS Reference Station Network. Geod. Cartogr. 2018, 44, 55–62. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D. Effect of annual signals on geodetic velocity. J. Geophys. Res. Solid Earth 2002, 107, ETG 9-1–ETG 9-11. [Google Scholar] [CrossRef]
- Dach, R.; Schaer, S.; Arnold, D.; Orliac, E.; Prange, L.; Susnik, A.; Villiger, A.; Jäggi, A. CODE Final Product Series for the IGS; Astronomical Institute, University of Bern: Bern, Switzerland, 2016. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Kierulf, H.P.; Plag, H.-P.; Bingley, R.M.; Teferle, N.; Demir, C.; Cingoz, A.; Yildiz, H.; Garate, J.; Davila, J.M.; Silva, C.G.; et al. Comparison of GPS analysis strategies for high-accuracy vertical land motion. Phys. Chem. Earth Parts A B C 2008, 33, 194–204. [Google Scholar] [CrossRef]
- Bos, M.; Fernandes, R. Hector User Manual Version 1.6 2016. Available online: http://segal.ubi.pt/hector/old_versions/manual_1.6.pdf (accessed on 13 May 2019).
- Langbein, J.; Bock, Y. High-rate real-time GPS network at Parkfield: Utility for detecting fault slip and seismic displacements. Geophys. Res. Lett. 2004, 31, 1–4. [Google Scholar] [CrossRef]
- Kleiner, B.; Graedel, T.E. Exploratory data analysis in the geophysical sciences. Rev. Geophys. 1980, 18, 699–717. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Andrei, C.-O.; Lahtinen, S.; Nordman, M.; Näränen, J.; Koivula, H.; Poutanen, M.; Hyyppä, J. GPS Time-series Analysis from Aboa the Finnish Antarctic Research Station. Remote Sens. 2018, 10, 1937. [Google Scholar] [CrossRef]
- Penna, N.T.; King, M.A.; Stewart, M.P. GPS height time-series: Short-period origins of spurious long-period signals. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Barbieri, M.M.; Berger, J.O. Optimal predictive model selection. Ann. Stat. 2004, 32, 870–897. [Google Scholar] [CrossRef]
- Yang, Y. Can the strengths of AIC and BIC be shared? A conflict between model indentification and regression estimation. Biometrika 2005, 92, 937–950. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time-series. J. Geophys. Res. Solid Earth 2002, 107, 9–16. [Google Scholar] [CrossRef]
- Klos, A.; Bogusz, J.; Figurski, M.; Kosek, W. On the Handling of Outliers in the GNSS Time-series by Means of the Noise and Probability Analysis. In IAG 150 Years; Rizos, C., Willis, P., Eds.; Springer International Publishing: Bern, Switzerland, 2016; pp. 657–664. [Google Scholar]
- Johnson, H.O.; Agnew, D.C. Monument motion and measurements of crustal velocities. Geophys. Res. Lett. 1995, 22, 2905–2908. [Google Scholar] [CrossRef]
- Klos, A.; Bogusz, J.; Figurski, M.; Kosek, W. Noise analysis of continuous GPS time-series of selected EPN stations to investigate variations in stability of monument types. In Proceedings of the VIII Hotine-Marussi Symposium on Mathematical Geodesy; Springer: Bern, Switzerland, 2015; pp. 19–26. [Google Scholar]
- Bogusz, J.; Rosat, S.; Klos, A.; Lenczuk, A. On the noise characteristics of time-series recorded with nearby located GPS receivers and superconducting gravity meters. Acta Geod. Geophys. 2018, 53, 201–220. [Google Scholar] [CrossRef]














| PARAMETER | BERN | GOA |
|---|---|---|
| Satellite system | GPS | GPS |
| Method | double difference (DD) | precise point positioning (PPP) |
| Elevation mask | 10° | 10° |
| Precise orbits and clocks | CODE final products | JPL final products |
| Antenna calibration file | epnc_08.atx | igs08.atx |
| Troposphere mapping function | VMF1 | VMF1 |
| Ocean loading tide model | FES2004 | FES2004 |
| Reference frame | ITRF2008 | ITRF2008 |
| Second order ionosphere correction | Yes | Yes |
| Station Name | GOA Time-Series | BERN Time-Series | ||||||
|---|---|---|---|---|---|---|---|---|
| Initial no of Points | Tsview 3-Sigma | Hector IQ = 2.2 | Hector IQ = 3 | Initial no of Points | Tsview 3-Sigma | Hector IQ = 2.2 | Hector IQ = 3 | |
| (GOA_1) | (GOA_2) | (GOA_3) | (BERN_1) | (BERN_2) | (BERN_3) | |||
| AUDR | 3144 | 5.6% | 3.2% | 0.9% | 3071 | 19.5% | 8.2% | 2.9% |
| KARD | 2822 | 10.0% | 6.0% | 2.4% | 2765 | 20.6% | 13.1% | 7.5% |
| KARG | 2562 | 7.2% | 6.0% | 3.4% | 2499 | 9.1% | 5.2% | 2.5% |
| KURE | 3277 | 4.5% | 2.6% | 0.4% | 3205 | 9.0% | 5.3% | 2.0% |
| MISS | 2626 | 4.3% | 3.2% | 0.6% | 2539 | 4.5% | 2.6% | 0.8% |
| MVEE | 2874 | 9.8% | 6.7% | 3.0% | 2838 | 15.8% | 12.0% | 5.5% |
| SUR4 | 3273 | 4.0% | 2.2% | 0.3% | 3188 | 10.2% | 6.4% | 2.9% |
| TOIL | 3272 | 5.3% | 2.7% | 0.4% | 3168 | 7.5% | 4.2% | 1.0% |
| TOR2 | 3204 | 3.9% | 2.2% | 0.4% | 3057 | 13.4% | 4.7% | 0.8% |
| VOR2 | 2795 | 22.5% | 14.7% | 6.4% | 2447 | 29.3% | 21.9% | 10.9% |
| Average | 7.7% | 4.9% | 1.8% | 13.9% | 8.4% | 3.7% | ||
| Noise Model | North | East | Up | Total SUM | % (NEU Component) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AIC | BIC | SUM | AIC | BIC | SUM | AIC | BIC | SUM | AIC | BIC | ||
| FN + RW | 0 | 0 | 0 | 1 | 1 | 2 | 5 | 7 | 12 | 14 | 20.0% | 26.7% |
| FN + WN | 3 | 8 | 11 | 8 | 9 | 17 | 0 | 0 | 0 | 28 | 36.7% | 56.7% |
| GGM | 7 | 2 | 9 | 1 | 0 | 1 | 5 | 3 | 8 | 18 | 43.3% | 16.7% |
| GGM + WN | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0% | 0.0% |
| PLN + WN | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0% | 0.0% |
| WN | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0% | 0.0% |
| Noise Model | North | East | Up | Total SUM | % (NEU Component) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AIC | BIC | SUM | AIC | BIC | SUM | AIC | BIC | SUM | AIC | BIC | ||
| FN + RW | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0% | 0.0% |
| FN + WN | 4 | 9 | 13 | 5 | 9 | 14 | 1 | 5 | 6 | 33 | 33.3% | 76.7% |
| GGM | 0 | 0 | 0 | 3 | 1 | 4 | 7 | 5 | 12 | 16 | 33.3% | 20.0% |
| GGM + WN | 6 | 1 | 7 | 2 | 0 | 2 | 2 | 0 | 2 | 11 | 33.3% | 3.3% |
| PLN + WN | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0% | 0.0% |
| WN | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0% | 0.0% |
| Noise Model | NKG2005-LU [41] | NKG2016-LU [10] | NKG2016-GIA [10] | D1 [42] | ICE-6G-(VM5a) [43] | BIFROST-2016 [10] |
|---|---|---|---|---|---|---|
| WN | 0.08 ± 0.36 | 0.16 ± 0.40 | 0.21 ± 0.63 | −0.30 ± 0.46 | −1.27 ± 0.86 | 0.27 ± 0.22 |
| PLN + WN | 0.08 ± 0.49 | 0.17 ± 0.56 | 0.21 ± 0.76 | −0.30 ± 0.58 | −1.26 ± 0.85 | 0.16 ± 0.27 |
| GGM | 0.08 ± 0.38 | 0.17 ± 0.43 | 0.21 ± 0.66 | −0.30 ± 0.48 | −1.26 ± 0.85 | 0.26 ± 0.23 |
| GGM + WN | 0.08 ± 0.38 | 0.17 ± 0.43 | 0.21 ± 0.65 | −0.30 ± 0.48 | −1.26 ± 0.85 | 0.26 ± 0.23 |
| FN + WN | 0.08 ± 0.37 | 0.16 ± 0.42 | 0.21 ± 0.64 | −0.30 ± 0.47 | −1.26 ± 0.85 | 0.27 ± 0.22 |
| FN + RW | 0.08 ± 0.38 | 0.16 ± 0.43 | 0.21 ± 0.66 | −0.30 ± 0.48 | −1.26 ± 0.85 | 0.26 ± 0.23 |
| Noise Model | NKG2005-LU [41] | NKG2016-LU [10] | NKG2016-GIA [10] | D1 [42] | ICE-6G-(VM5a) [43] | BIFROST-2016 [10] |
|---|---|---|---|---|---|---|
| WN | 0.17 ± 0.40 | 0.26 ± 0.45 | 0.30 ± 0.67 | −0.21 ± 0.51 | −1.17 ± 0.86 | 0.28 ± 0.20 |
| PLN + WN | 0.10 ± 0.41 | 0.19 ± 0.47 | 0.24 ± 0.69 | −0.27 ± 0.52 | −1.24 ± 0.85 | 0.24 ± 0.17 |
| GGM | 0.14 ± 0.42 | 0.23 ± 0.47 | 0.27 ± 0.69 | −0.23 ± 0.53 | −1.20 ± 0.86 | 0.26 ± 0.19 |
| GGM + WN | 0.15 ± 0.42 | 0.23 ± 0.48 | 0.28 ± 0.70 | −0.23 ± 0.53 | −1.19 ± 0.85 | 0.27 ± 0.19 |
| FN + WN | 0.14 ± 0.42 | 0.22 ± 0.48 | 0.27 ± 0.69 | −0.24 ± 0.53 | −1.20 ± 0.86 | 0.26 ± 0.18 |
| FN + RW | 0.14 ± 0.42 | 0.22 ± 0.48 | 0.27 ± 0.70 | −0.24 ± 0.53 | −1.20 ± 0.85 | 0.26 ± 0.18 |
| Noise Model | NKG2005-LU [41] | NKG2016-LU [10] | NKG2016-GIA [10] | D1 [42] | ICE-6G-(VM5a) [43] | BIFROST-2016 [10] |
|---|---|---|---|---|---|---|
| GOA (MIDAS) | 0.20 ± 0.31 | 0.29 ± 0.34 | 0.33 ± 0.55 | −0.18 ± 0.42 | −1.14 ± 0.88 | 0.34 ± 0.21 |
| GOA (Tsview) | 0.07 ± 0.36 | 0.15 ± 0.40 | 0.20 ± 0.62 | −0.31 ± 0.46 | −1.28 ± 0.86 | 0.28 ± 0.22 |
| BERN (MIDAS) | 0.05 ± 0.43 | 0.13 ± 0.46 | 0.18 ± 0.64 | −0.33 ± 0.51 | −1.30 ± 0.91 | 0.11 ± 0.27 |
| BERN (Tsview) | 0.16 ± 0.39 | 0.25 ± 0.45 | 0.29 ± 0.67 | −0.22 ± 0.51 | −1.18 ± 0.86 | 0.28 ± 0.19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kall, T.; Oja, T.; Kollo, K.; Liibusk, A. The Noise Properties and Velocities from a Time-Series of Estonian Permanent GNSS Stations. Geosciences 2019, 9, 233. https://doi.org/10.3390/geosciences9050233
Kall T, Oja T, Kollo K, Liibusk A. The Noise Properties and Velocities from a Time-Series of Estonian Permanent GNSS Stations. Geosciences. 2019; 9(5):233. https://doi.org/10.3390/geosciences9050233
Chicago/Turabian StyleKall, Tarmo, Tõnis Oja, Karin Kollo, and Aive Liibusk. 2019. "The Noise Properties and Velocities from a Time-Series of Estonian Permanent GNSS Stations" Geosciences 9, no. 5: 233. https://doi.org/10.3390/geosciences9050233
APA StyleKall, T., Oja, T., Kollo, K., & Liibusk, A. (2019). The Noise Properties and Velocities from a Time-Series of Estonian Permanent GNSS Stations. Geosciences, 9(5), 233. https://doi.org/10.3390/geosciences9050233