Effects of Class Purity of Training Patch on Classification Performance of Crop Classification with Convolutional Neural Network †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Areas and Datasets
2.1.1. Case 1: Anbandegi in Korea
2.1.2. Case 2: Illinois in United States
2.2. Sampling of Training Patch
2.2.1. Sampling Design Using Class Purity
2.2.2. Defining Class Homogeneity of Study Area
2.3. 2D-CNN Model
2.4. Experimental Design
2.4.1. Parameter Setting for Effect Analysis
2.4.2. Preparation of Training and Reference Datasets and Accuracy Evaluation
3. Results
3.1. Comparison of Class Homogeneity of Two Regions
3.2. Classification Results in the Anbandegi Region
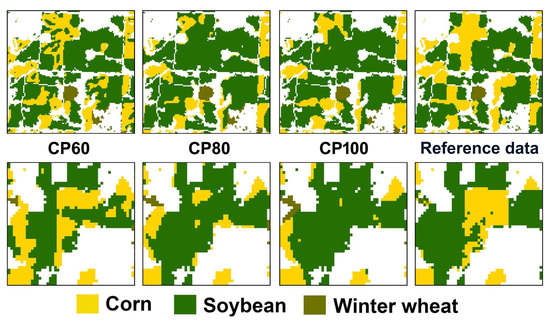
3.3. Classification Results in the Illinois Region
4. Discussion
4.1. Novelty of the Study and Implications for Training Sample Selection
4.2. Limitations and Future Research Directions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef] [Green Version]
- Kwak, G.-H.; Park, S.; Yoo, H.Y.; Park, N.-W. Updating land cover maps using object segmentation and past land cover information. Korean J. Remote Sens. 2017, 33, 1089–1100, (In Korean with English Abstract). [Google Scholar]
- Na, S.-I.; Park, C.-W.; So, K.-H.; Ahn, H.-Y.; Lee, K.-D. Development of biomass evaluation model of winter crop using RGB imagery based on unmanned aerial vehicle. Korean J. Remote Sens. 2018, 34, 709–720, (In Korea with English Abstract). [Google Scholar]
- Lee, Y.-S.; Lee, S.; Jung, H.-S. Mapping forest vertical structure in Gong-ju, Korea using Sentinel-2 satellite images and artificial neural networks. Appl. Sci. 2020, 10, 1666. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Park, N.-W.; Lee, K.-D. Self-learning based land-cover classification using sequential class patterns from past land-cover maps. Remote Sens. 2017, 9, 921. [Google Scholar] [CrossRef] [Green Version]
- Zurqani, H.A.; Post, C.J.; Mikhailova, E.A.; Allen, J.S. Mapping urbanization trends in a forested landscape using Google Earth Engine. Remote Sens. Earth Syst. Sci. 2019, 2, 173–182. [Google Scholar] [CrossRef]
- Kwak, G.-H.; Park, N.-W. Impact of texture information on crop classification with machine learning and UAV images. Appl. Sci. 2019, 9, 643. [Google Scholar] [CrossRef] [Green Version]
- Belgiu, M.; Drǎguţ, L. Comparing supervised and unsupervised multiresolution segmentation approaches for extracting buildings from very high resolution imagery. ISPRS J. Photogramm. Remote Sens. 2014, 96, 67–75. [Google Scholar] [CrossRef] [Green Version]
- Foody, G.M.; Mathur, A. The use of small training sets containing mixed pixels for accurate hard image classification: Training on mixed spectral responses for classification by a SVM. Remote Sens. Environ. 2006, 103, 179–189. [Google Scholar]
- Mathur, A.; Foody, G.M. Crop classification by support vector machine with intelligently selected training data for an operational application. Int. J. Remote Sens. 2008, 29, 2227–2240. [Google Scholar]
- Shao, Y.; Lunetta, R.S. Comparison of support vector machine, neural network, and CART algorithms for the land-cover classification using limited training data points. ISPRS J. Photogramm. Remote Sens. 2012, 70, 78–87. [Google Scholar] [CrossRef]
- Millard, K.; Richardson, M. On the importance of training data sample selection in random forest image classification: A case study in peatland ecosystem mapping. Remote Sens. 2015, 7, 8489–8515. [Google Scholar] [CrossRef] [Green Version]
- Villa, A.; Chanussot, J.; Benediktsson, J.A.; Jutten, C. Spectral unmixing for the classification of hyperspectral images at a finer spatial resolution. IEEE J. Sel. Topics Signal Process. 2010, 5, 521–533. [Google Scholar] [CrossRef] [Green Version]
- Foody, G.M.; Arora, M.K. Incorporating mixed pixels in the training, allocation and testing stages of supervised classifications. Pattern Recog. Lett. 1996, 17, 1389–1398. [Google Scholar] [CrossRef]
- Brown, M.; Gunn, S.R.; Lewis, H.G. Support vector machines for optimal classification and spectral unmixing. Ecol. Model. 1999, 120, 167–179. [Google Scholar] [CrossRef]
- Mianji, F.A.; Zhang, Y. SVM-based unmixing-to-classification conversion for hyperspectral abundance quantification. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4318–4327. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, X.; Gao, L.; Yang, L. Endmember extraction of hyperspectral remote sensing images based on the ant colony optimization (ACO) algorithm. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2635–2646. [Google Scholar] [CrossRef]
- Yang, C.; Wu, G.; Ding, K.; Shi, T.; Li, Q.; Wang, J. Improving land use/land cover classification by integrating pixel unmixing and decision tree methods. Remote Sens. 2017, 9, 1222. [Google Scholar] [CrossRef] [Green Version]
- Kavzoglu, T. Increasing the accuracy of neural network classification using refined training data. Environ. Model. Softw. 2009, 24, 850–858. [Google Scholar] [CrossRef]
- Ozdarici Ok, A.; Akyurek, Z. Automatic training site selection for agricultural crop classification: A case study on Karacabey plain, Turkey. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 3819, 221–225. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Stow, D. The effect of training strategies on supervised classification at different spatial resolutions. Photogramm. Eng. Remote Sens. 2002, 68, 1155–1162. [Google Scholar]
- Chen, Y.; Song, X.; Wang, S.; Huang, J.; Mansaray, L.R. Impacts of spatial heterogeneity on crop area mapping in Canada using MODIS data. ISPRS J. Photogramm. Remote Sens. 2016, 119, 451–461. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing data: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional neural networks for large-scale remote-sensing image classification. IEEE Trans. Geosci. Remote Sens. 2016, 55, 645–657. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.-Y.; Xia, Q.-M.; Yan, J.-W.; Xuan, S.-Q.; Su, J.-H.; Yang, C.-F. Hyperspectral image classification based on spectral and spatial information using multi-scale ResNet. Appl. Sci. 2019, 9, 4890. [Google Scholar] [CrossRef] [Green Version]
- Park, M.-G.; Kwak, G.-H.; Park, N.-W. A convolutional neural network model with weighted combination of multi-scale spatial features for crop classification. Korean J. Remote Sens. 2019, 35, 1273–1283, (In Korean with English Abstract). [Google Scholar]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Kwak, G.-H.; Lee, K.-D.; Na, S.-I.; Park, C.-W.; Park, N.-W. Performance evaluation of machine learning and deep learning algorithms in crop classification: Impact of hyper-parameters and training sample size. Korean J. Remote Sens. 2018, 34, 811–827, (In Korean with English Abstract). [Google Scholar]
- Sharma, A.; Liu, X.; Yang, X.; Shi, D. A patch-based convolutional neural network for remote sensing image classification. Neural Netw. 2017, 95, 19–28. [Google Scholar]
- Song, H.; Kim, Y.; Kim, Y. A patch-based light convolutional neural network for land-cover mapping using Landsat-8 images. Remote Sens. 2019, 11, 114. [Google Scholar]
- Kwak, G.-H.; Park, M.-G.; Park, C.-W.; Lee, K.-D.; Na, S.-I.; Ahn, H.-Y.; Park, N.-W. Combining 2D CNN and bidirectional LSTM to consider spatio-temporal features in crop classification. Korean J. Remote Sens. 2019, 35, 681–692, (In Korean with English Abstract). [Google Scholar]
- Muñoz-Marí, J.; Bruzzone, L.; Camps-Valls, G. A support vector domain description approach to supervised classification of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2683–2692. [Google Scholar] [CrossRef]
- Zhu, Z.; Gallant, A.L.; Woodcock, C.E.; Pengra, B.; Olofsson, P.; Loveland, T.R.; Jin, S.; Dahal, D.; Yang, L.; Auch, R.F. Optimizing selection of training and auxiliary data for operational land cover classification for the LCMAP initiative. ISPRS J. Photogramm. Remote Sens. 2016, 122, 206–221. [Google Scholar] [CrossRef] [Green Version]
- Cracknell, M.J.; Reading, A.M. Geological mapping using remote sensing data: A comparison of five machine learning algorithms, their response to variations in the spatial distribution of training data and the use of explicit spatial information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef] [Green Version]
- Environmental Geographic Information Service (EGIS). Available online: http://egis.me.go.kr (accessed on 1 August 2019).
- USGS Global Visualization Viewer (GloVis). Available online: https://glovis.usgs.gov (accessed on 12 August 2019).
- CropScape. Available online: https://nassgeodata.gmu.edu/CropScape (accessed on 12 August 2019).
- Löw, F.; Duveiller, G. Defining the spatial resolution requirements for crop identification using optical remote sensing. Remote Sens. 2014, 6, 9034–9063. [Google Scholar]
- Ji, S.; Zhang, C.; Xu, A.; Shi, Y.; Duan, Y. 3D convolutional neural network for crop classification with multi-temporal remote sensing images. Remote Sens. 2018, 10, 75. [Google Scholar] [CrossRef] [Green Version]
- Lillesand, T.M.; Kiefer, R.W.; Chipman, J.W. Remote Sensing and Image Interpretation, 6th ed.; Wiley: Hoboken, NJ, USA, 2008; pp. 585–586. [Google Scholar]
- Smith, J.H.; Wickham, J.D.; Stehman, S.V.; Yang, L. Impacts of patch size and land-cover heterogeneity on thematic image classification accuracy. Photogramm. Eng. Remote Sens. 2002, 68, 65–70. [Google Scholar]
- Smith, J.H.; Stehman, S.V.; Wickham, J.D.; Yang, L. Effects of landscape characteristics on land-cover class accuracy. Remote Sens. Environ. 2003, 84, 342–349. [Google Scholar] [CrossRef]
- Foody, G.M. The significance of border training patterns in classification by a feedforward neural network using back propagation learning. Int. J. Remote Sens. 1999, 20, 3549–3562. [Google Scholar] [CrossRef]
- Liu, J.; Liu, H.; Heiskanen, J.; Mõttus, M.; Pellikka, P. Posterior probability-based optimization of texture window size for image classification. Remote Sens. Lett. 2014, 5, 753–762. [Google Scholar] [CrossRef]
- Scott, G.J.; England, M.R.; Starms, W.A.; Marcum, R.A.; Davis, C.H. Training deep convolutional neural networks for land-cover classification of high-resolution imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 549–553. [Google Scholar] [CrossRef]
- Bradley, P.E.; Keller, S.; Weinmann, M. Unsupervised feature selection based on ultrametricity and sparse training data: A case study for the classification of high-dimensional hyperspectral data. Remote Sens. 2018, 10, 1564. [Google Scholar] [CrossRef] [Green Version]
- Adams, J.B.; Sabol, D.E.; Kapos, V.; Filho, R.A.; Roberts, D.A.; Smith, M.O.; Gillespie, A.R. Classification of multispectral images based on fractions of endmembers: Application to land-cover change in the Brazilian Amazon. Remote Sens. Environ. 1995, 52, 137–154. [Google Scholar]
- Zhao, J.; Zhong, Y.; Hu, X.; Wei, L.; Zhang, L. A robust spectral-spatial approach to identifying heterogeneous crops using remote sensing imagery with high spectral and spatial resolutions. Remote Sens. Environ. 2020, 239, 111605. [Google Scholar] [CrossRef]









| Category | Specification |
|---|---|
| UAV model | eBee Classic |
| Camera | Canon IXUS/ELPH |
| Image size | 2629 by 3275 |
| Area of crop parcels | 28.7 ha |
| Spectral bands | Blue, Green, Red |
| Spatial resolution | 0.25 m |
| Acquisition date | 25 August 2017 |
| Category | Specification |
|---|---|
| Satellite/Sensor | Landsat-8 OLI |
| Image size | 633 by 673 |
| Area of crop parcels | 198,476 ha |
| Spectral bands | Red, NIR, SWIR |
| Spatial resolution | 30 m |
| Acquisition date | 7 March 2017 |
| 8 April 2017 | |
| 27 May 2017 | |
| 15 September 2017 | |
| 17 October 2017 |
| Layer Type/Method | Output Dimension | Number of Parameters |
|---|---|---|
| Conv2D_1 | (P, P, F) | 896 |
| Conv2D_2 | (P, P, F) | 9248 |
| Max-pooling2D | (P/2, P/2, F) | 0 |
| Conv2D_3 | (P/2, P/2, F × 2) | 18,496 |
| Dropout | 256 neurons | 0 |
| Flattening | 256 neurons | 0 |
| ReLu | 64 neurons | 16,448 |
| Softmax | 4 neurons | 260 |
| Classifier | Parameters | Value | |
|---|---|---|---|
| Anbandegi | Illinois | ||
| 2D-CNN | Dropout rate | 0.2 | |
| Patch size | 5, 9, 13, 17, 21 | 5, 9, 15 | |
| Kernel size | 3 | ||
| Number of filters | 32 | ||
| CP60 | CP80 | CP100 | ||||
|---|---|---|---|---|---|---|
| PA (%) | UA (%) | PA (%) | UA (%) | PA (%) | UA (%) | |
| Highland Kimchi cabbage | 94.79 | 82.70 | 95.08 | 87.71 | 93.12 | 88.91 |
| Cabbage | 72.16 | 87.52 | 71.89 | 92.40 | 72.66 | 94.85 |
| Potato | 90.12 | 84.96 | 95.12 | 74.02 | 96.57 | 77.75 |
| Fallow | 49.50 | 79.62 | 58.00 | 79.59 | 73.55 | 74.82 |
| OA (%) | 83.78 | 85.49 | 86.56 | |||
| CP60 | CP80 | CP100 | ||||
|---|---|---|---|---|---|---|
| PA (%) | UA (%) | PA (%) | UA (%) | PA (%) | UA (%) | |
| Corn | 82.13 | 73.76 | 80.61 | 73.22 | 74.83 | 72.00 |
| Soybean | 76.87 | 86.76 | 77.42 | 86.11 | 75.96 | 82.32 |
| Winter wheat | 95.06 | 83.96 | 90.09 | 80.76 | 90.86 | 77.56 |
| OA (%) | 81.43 | 80.44 | 77.87 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.; Park, N.-W. Effects of Class Purity of Training Patch on Classification Performance of Crop Classification with Convolutional Neural Network. Appl. Sci. 2020, 10, 3773. https://doi.org/10.3390/app10113773
Park S, Park N-W. Effects of Class Purity of Training Patch on Classification Performance of Crop Classification with Convolutional Neural Network. Applied Sciences. 2020; 10(11):3773. https://doi.org/10.3390/app10113773
Chicago/Turabian StylePark, Soyeon, and No-Wook Park. 2020. "Effects of Class Purity of Training Patch on Classification Performance of Crop Classification with Convolutional Neural Network" Applied Sciences 10, no. 11: 3773. https://doi.org/10.3390/app10113773
APA StylePark, S., & Park, N. -W. (2020). Effects of Class Purity of Training Patch on Classification Performance of Crop Classification with Convolutional Neural Network. Applied Sciences, 10(11), 3773. https://doi.org/10.3390/app10113773