Injury Biomechanics of a Child’s Head: Problems, Challenges and Possibilities with a New aHEAD Finite Element Model

Abstract

Traumatic brain injury (TBI) is a major public health problem among children. The predominant causes of TBI in young children are motor vehicle accidents, firearm incidents, falls, and child abuse. The limitation of in vivo studies on the human brain has made the finite element modelling an important tool to study brain injury. Numerical models based on the finite element approach can provide valuable data on biomechanics of brain tissues and help explain many pathological conditions. This work reviews the existing numerical models of a child’s head. However, the existing literature is very limited in reporting proper geometric representation of a small child’s head. Therefore, an advanced 2-year-old child’s head model, named aHEAD 2yo (aHEAD: advanced Head models for safety Enhancement And medical Development), has been developed, which advances the state-of-the-art. The model is one of the first published in the literature, which entirely consists of hexahedral elements for three-dimensional (3D) structures of the head, such as the cerebellum, skull, and cerebrum with detailed geometry of gyri and sulci. It includes cerebrospinal fluid as Smoothed Particle Hydrodynamics (SPH) and a detailed model of pressurized bringing veins. Moreover, the presented review of the literature showed that material models for children are now one of the major limitations. There is also no unambiguous opinion as to the use of separate materials for gray and white matter. Thus, this work examines the impact of various material models for the brain on the biomechanical response of the brain tissues during the mechanical loading described by Hardy et al. The study compares the inhomogeneous models with the separation of gray and white matter against the homogeneous models, i.e., without the gray/white matter separation. The developed model along with its verification aims to establish a further benchmark in finite element head modelling for children and can potentially provide new insights into injury mechanisms.

1. Introduction

Brain injuries are the leading cause of death among the paediatric population. Surveillance data reveals that 1 in every 20 emergency department presentations at paediatric hospitals is for a TBI (traumatic brain injury), making TBIs more common than burns or poisonings. For children, such injuries represent a common interruption to the normal growing up [1].

Statistics show that 95% of all children who have suffered from TBI survive. In contrast, only 65% of the children who have experienced severe TBI survive. The highest mortality occurs in children who are less than 2 years old. TBI mortality rates are gradually decreasing to the age of 12, and then the second peak in mortality is observed at the age of 15 years [2].

TBI overtakes other common paediatric fatal diseases such as congenital malformations and oncological disease [3,4]. Recent studies have shown that the mortality rate of TBI was as high as 8.99 per 100,000 population by the end of the 20th century. It began to decrease in the next 15 years to 4.42 and since then, unfortunately, it increased up to the ratio of 5.17 [5]. Thanks to the implementation of safety regulations, passive safety devices and the development of modern treatment methods, the number has decreased, yet it still requires action for further improvement [6,7,8,9]. TBI can cause a serious burden to a child’s life and even in cases of good recovery, long-lasting behavioural problems after paediatric TBI can be found in up to 33% of the survivors [3,10,11]. It is not always evident if these long-lasting posttraumatic changes are related to brain contusions or rather microinjuries to white matter structure [12,13]. TBI also comes with higher treatment costs than any other kind of trauma, and typically requires a longer time of treatment and rehabilitation. Patients more often need repeated medical assistance and a higher number of hospital readmissions [14].

Apart from prevention of injuries, a method in case of severe medical conditions shall be developed to enable medical professionals to have an early selection of patients who are at higher risk of unfavourable progression of the disease. These patients would require intensive care and monitoring from admission to hospital. Biomechanical simulations based on the finite element method can be implemented to reconstruct the probable mechanism of injury [15]. However, as it provides information of value in case of legal aspects, from daily medical practice, it is more important to provide a reliable prognosis. Biomechanical testing may provide information on future trauma development and pinpoint possible points of weakness after injury [16]. To foresee how the injury will develop is of utmost importance and provides information as to whether intense clinical and radiological monitoring may be necessary.

It should be noted that TBI in children is a serious social problem. At the same time, since there is limited data obtained from radiological imaging (due to invasiveness and limited use of computed tomography in the children population), recognition of mechanics of brain tissue damage is somewhat hindered. Computed Tomography (CT) is rarely used in the infant population because it induces high-dose radiation and consequently becomes almost the last resort.

At the same time, it should be emphasized that one of the best methods for biomechanical assessment of human tissues is experimental research. However, it is obvious that obtaining human cadaveric specimens, in particular children, is practically impossible or ethically biased. Animal studies are an alternative. Due to some similarity in the structure of some brain tissues, pig specimens are one of the most frequently used samples. Nevertheless, they do not allow a complete reference to the human system. In addition, they do not provide a comprehensive insight into the tissues’ interactions under mechanical loads. Hence, numerical models are currently one of the best solutions for biomechanical evaluation. However, a literature review shows that there is presently a serious gap in the numerical head models of young children. This is due to the limited availability of medical data of young children without pathologies. Moreover, the development of a child is highly nonlinear, among others biased by genetics and its environment. The uncertainty of where to find the gathered data within the broad range of the regional population increases the difficultness of validation or even makes it impossible.

Therefore, in this work, the authors present current problems, challenges, and opportunities for modelling the head of a small child. Bearing in mind the current knowledge in the field of numerical modelling, the authors present their original head model of a small child based on the finite element (FE) approach. The model of a 2-year-old (2yo) child’s head is an outcome of interdisciplinary research and it is a part of a holistic project, aHEAD (advanced Head models for safety Enhancement and medical Development [17])—thus, it bears the name aHEAD 2yo. A method for verifying the developed model was also proposed. The developed model along with its verification aims to establish a further benchmark.

2. Injury Biomechanics of Small Children

2.1. Pediatric Anthropometry

The proportions of individual body regions change significantly from birth to adult age [18,19]. The shape of the head changes from birth to adulthood (Figure 1). For an infant, the face is a very small part of the total head volume. The facial portion of the head at birth is smaller than the cranium, having a face-to-cranium ratio of 1:8 compared to the ratio of 1:2.5 for adults [20]. Interestingly, at birth, the head is often more than 1:4 of the total body length, whereas in the adult, it is approximately 1:7.

2.2. Injury Types

The most common mechanisms of brain injury include falls, collisions, projectiles, and punches [22,23]. Falls are the most common mechanism of TBI [24]. Short-distance falls are a common cause of trauma in young children, and an important topic in forensic science in cases of child abuse. This kind of injury results in impacts with high-magnitude and short-duration linear and rotational acceleration [25]. Low compliance of hard impact surfaces (e.g., ground) must be taken into consideration.

Coats et al. [26] showed that coronal rotation in similar cases was minimal and axial head rotation resulted in higher peak angular accelerations than sagittal rotation, most probably due to the convexity of the occipital region and neck’s laxity. Ibrahim et al. [27] pointed out that infants sustained more skull fractures than toddlers (71% versus 39%) from short-distance falls. These resulted in primary intracranial injury without soft tissue or skull injury in infants (6%) and toddlers (16%). Sullivan et al. [28] indicated fall height and impact site as crucial conditions for predicting the extent of the injury. Impact on occipital and parietal areas produced greater angular velocities as the head rebounded after impacts.

In comparison with falls and collisions, brain injuries induced by punches and projectiles are characterized by lower effective mass and higher velocity [29]. Moreover, the compliance of the human fist is greater than the compliance of hard surfaces [30]. Therefore, the velocity of the impacting object and the impacted region have a determining role in such low-mass events. For example, the further the impact lands outside of the centre of gravity, the greater the rotational acceleration will be, which is a significant issue in most TBIs [31,32].

Intracranial haemorrhagic trauma is a result of short-duration events (5 ms) [28]. Overall, contusions and epidural hematomas (EDH) are more related to linear acceleration, while subdural hematomas (SDH) and traumatic subarachnoid haemorrhage are more closely related with rotational acceleration [33]. Diffuse axonal injury (DAI) is also rotationally dominant and present especially in high acceleration-deceleration, with head rotation impacts such as traffic accidents [34,35,36,37]. In a paper by Ibrahim et al. [38], scaling rotational accelerations from the 4-week-old toddler piglets to the 5-day-old infant animals by brain mass alone resulted in more severe subarachnoid haemorrhage and white matter injury in the younger group. This is probably due to greater stiffness of the younger brain, which requires three times lower strain to produce a similar haemorrhage [38].

Frequency of TBI in up to 4-year-old patients is twice the rate of TBI in the next most affected population (15–24 years old) [39]. Most of these injuries are limited to mild TBI, mainly concussions, which can be defined as a clinical syndrome of biomechanically induced alteration of brain function, typically affecting memory and orientation, which may involve loss of consciousness. The occurrence of concussion in children under 15 years old is 692/100,000 [39]. Most of the patients with mild TBI do not present symptoms that necessitate further diagnostics, e.g., computed tomography (CT), therefore most radiological data from the paediatric population comes from patients diagnosed with a medium to severe trauma. Space occupying lesions, which are the result of primary injury of brain parenchyma and injuries of major intracranial vessels, fall into this category.

Epidural bleeding, which is usually a result of middle meningeal artery rupture, is more common in younger people than in the elderly. In children, epidural hematomas usually have a less severe course than in young adults, and the hematomas tend to be relatively smaller in the paediatric population. SDH is quite frequent in infants—especially in those suffering from domestic abuse [40]. In children, similarly to adults, bridging veins are the origin of the bleeding. On the other hand, in a paper by Raul et al. [40], in contrary to the elderly population, it was shown that enlargement of subdural space in infants does not have a significant impact on the risk of SDH. Posttraumatic subarachnoid haemorrhages are also commonly seen in paediatric patients.

2.3. Cases of Medical Injuries

Minor injuries come as about one-fifth of cases referring to emergency departments [41]. CT scanning cannot and should not be used in every case because of radiation exposure. But, even when applied, the result cannot rule out all the uncertainty. Figure 2 presents two selected clinical cases depicting the brain hematoma and skull fractures.

3. Numerical Models of Paediatric Heads—State-of-the-Art

Biomechanical systems of the human body are very difficult to model due to the complex geometry, heterogeneity, nonlinear behaviour of the materials involved and complex boundary conditions [42,43,44,45]. It is particularly difficult to map the biomechanics of the head of a small child. This difficulty is caused by a rapid change in the head geometry and changes in the mechanical properties of the child’s bone and tissue structures with age. Due to the tightened legal regulations and very rare availability of paediatric corpses, determining the mechanical parameters of tissues for this age group is considerably difficult. This, in turn, is the main limiting factor in FE (finite element) models of paediatric heads.

Table 1. Numerical models of paediatric heads presented in current literature.

Validation	Material Law	Mesh Elements	Geometry	FE Solver	Age	FE Mesh	Reference
None	Linear viscoelastic brain, linear elastic bone (interpolated)/suture/cerebrospinal fluid (CSF)/scalp	6 -month-old: 69,324 solid elements, 9187 shell elements 3-year-old: 23,000 solid elements, 3500 shell elements	3D, CT	Radioss	6 months/3 years		Roth et al., 2007, 2009 [46,47]
None	Linear viscoelastic brain, linear elastic bone/suture/CSF/scalp	not available	3D, CT	LS-DYNA	6 months		DeSantis Klinich, Hulbert, and Schneider, 2002 [48] (Desantis Klinich, Hulbert, and Schneider 2002)
Skull fracture location as predicted by ultimate stress	Ogden brain, orthotropic linear elastic bone, linear elastic suture and scalp	11,066 tetrahedral solid elements, 624 hexagonal solid elements, 18,706 shell elements, 2485 membrane elements	3D CT, Magnetic Resonance Imaging (MRI), suture geometry idealised	ABAQUS/Explicit	1.5 months		Coats, Margulies, and Ji, 2007 [49]
None	Linear viscoelastic brain, linear elastic bone/suture	12,772 elements	3D Idealised	ANSYS/LSDYNA3D	1 month		Margulies and Thibault 2000 [50]
None	Ogden brain, Rigid skull and falx	5834 elements	Pseudo 3D	PATRAN	2 weeks		Prange, Kiralyfalvi, and Margulies, 1999 [51]

summarizes the current models of paediatric heads depicted in the literature.

To represent a paediatric head numerically, appropriate geometry, material properties, and boundary conditions need to be defined. Analysing the current state of scientific articles and comparing to adult versions, the low number of paediatric is noticeable.

3.1. Validation and Verification of Computational Paediatric Models

Verification and validation of developed numerical models is the final possibility for researchers to prove and state the applicability and meaningfulness of their work by reflecting and presenting the real biological response. In a different outcome, this step might also reveal a gap, which helps to realise and point out an approach’s limitations. The general path for this is based on an accurately represented geometry in the discrete model with an accordingly approved mesh quality. A consecutive step is the implementation of case-specific information such as boundary conditions and mechanical properties. This is based on both appropriate testing procedures and specimens. The verification or validation of paediatric numerical models faces at this point a significant limitation, which is found in two aspects: the availability of specimens as well as clear experimental data for comparison. As mentioned, the highly non-linear nature of development of a child can be found also in the material properties. Consequently, it is the missing dataset over the entirety of the population which intensifies the problem to define an age-dependent average for material properties in this early stage of life. Moreover, while real-world experiments are strongly connected to ethical questions, the rarely available specimen tend to be from the upper range of the age span. In a consequence, real-world accident data and reconstruction by human surrogates is widely used as a substitutional path. Nonetheless, biofidelity might be not given by this approach in detail and covers partially the clear view on the basing injury mechanisms. Furthermore, scaling adult anthropometry for paediatric models has been applied many times in FEHMs, but is denied for the clear research about paediatric-specific injury biomechanics [52]. Nonetheless, the bottleneck is established by the missing or limited evidential material and experimental data over the entirety of the population. Therefore, researchers proposed a substitutional approach. Thereby, the strict requirement of implementing an appropriate in-detail geometry and quality within the mesh is accepted as a base, meaning that further developed models should decrease the current simplifications. Then, with an intense focus on the appropriate interpretation and discussion of the simulative results, a contribution to the scientific research can be achieved. The rigorous comparison of the achieved simulations to real-world (accident) cases is another supportive asset.

3.2. Mechanical Properties of the Brain Tissue Structures

During biological human development, the structures undergo significant physical changes. Therefore, the mechanical properties of brain tissues in individual age groups may show significant differences. These can be most visible up to an age of six [53]. Currently, there is little data in the literature regarding differences in mechanical properties in individual age groups during child development. The studies, which have been presented so far, have shown that brain tissue is a very soft non-linear viscoelastic solid material, with a very low linear viscoelastic strain limit in the range of 0.1–0.3%. In addition, brain tissue is strain rate-dependent. This soft tissue increases its stiffness as the deformation rate increases [54,55]. Depending on the type of load, tissue damage occurs at 25–100% strain. However, it should be noted that still, little is known about the mechanical properties of brain tissue due to inconsistent data presented in the current literature. Although it is known that brain tissue is anisotropic, the anisotropy of the axonal fibre bundle of white matter has not been comprehensively established. Between grey and white matter, there might be some differences in mechanical properties, which is associated with their structural difference (Table 2). Grey matter contains a densely packed network of neural cell bodies and associated glial cells. In contrast, white matter contains myelinated axonal tracts, relatively few neuronal cell bodies, and a supporting environment of glial cells.

In addition, some researchers have shown that there are regional differences in mechanical properties in individual regions. Conversely, it should be kept in mind that between individual authors, there are significant differences in the description of the mechanical properties of brain tissues [56,57,58]. This phenomenon may be associated with a different methodological approach, including the freshness and hydration of the tested samples.

Table 2. Brain tissue composition [59,60,61].

	Water (wt%)	Ash (wt%)	Lipid (wt%)	Protein (wt%)
Whole brain	76.3–78.5 (77.4)	1.4–2 (1.5)	9–17	8–12
Grey matter	83–86	1.5	5.3	8–12
White matter	68–77	1.4	18	11–12

Table 2. Brain tissue composition [59,60,61].

	Water (wt%)	Ash (wt%)	Lipid (wt%)	Protein (wt%)
Whole brain	76.3–78.5 (77.4)	1.4–2 (1.5)	9–17	8–12
Grey matter	83–86	1.5	5.3	8–12
White matter	68–77	1.4	18	11–12

It should be noted that few scientists have studied the mechanical properties of brain tissue depending on age. Nevertheless, they showed that the mechanical properties of the tissue differ significantly between age groups. The average weight of a human brain after birth is usually 350 to 450 g and continues to grow rapidly up to about 2 years. Prange and Margulies [57] took fresh samples of the cerebral cortex of grey matter from a 5-year-old and tested it within 3 h of its collection. For comparison, this cerebral cortex was also collected from an adult. This study showed that the brains of 5-year-olds were stiffer than the brains of adults.

At the same time, Sack et al. [62] performed magnetic resonance elastography (MRE) on using in vivo samples and found that the brain tissue modulus decreases with age, from early adulthood to old age. It is worth noting that the authors came to similar conclusions by conducting animal experiments and comparing results from young and older individuals. Significantly higher brain tissue stiffness was observed in juveniles [57,63,64]. However, it should be noted that the mechanical properties between different animal species can differ significantly. Nevertheless, the differences between the measured properties of brain tissue have been discussed for decades (

Table 3. Mechanical properties of brain tissues from paediatric heads.

Reference	Tissue	Research Method	Mechanical Properties	Age
Prange and Margulies, 2002 [57]	Brain (temporal cortex)	Shear stress–relaxation	Instantaneous shear modulus: 304 Pa	5 years
Kriewall et al., 1983; Bylski et al., 1986 [69,70]	Dura	Axisymmetric tension Biaxial tension	Stiffness: 3.377 ± 1.052 N/m 1.814 ± 590 N/m	30–42 weeks gest
Meaney, 1991 [71]	Bridging veins	Uniaxial tension	Stiffness: 235 ± 199 N/m Ultimate stress: 12.02 ± 5.9 MPa Stretch ratio: 1.67 ± 0.27	3–9 years

). Some studies show immediate significant decreases in brain stiffness after death [65,66,67,68].

4. Materials and Methods

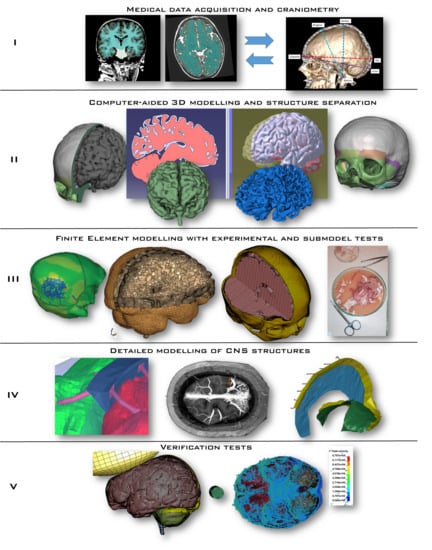
Several stages are necessary to develop a high-fidelity numerical model of the human head, from medical imaging to geometry segmentation, ending with the development of the FE model and its validation, as seen in the literature [72,73,74,75,76]. Depending on the degree of complexity and desired accuracy, this methodology can go from an almost straightforward task to an extremely time-consuming work, e.g., when aiming for the detailed modelling of the central nervous system (CNS) structures. In this section, the authors present their numerical model of a young child’s head. Its development was carried out in five well-defined stages (Figure 3):

I

Medical data acquisition and craniometry verification/measurement

II

Computer-aided design—3D modelling and structural segmentation/separation

III

Finite element modelling supported on experimental and sub-model testing

IV

Detailed model of CNS structures

V

Verification tests

The first stage consists of gathering medical data and extracting the regions of interest for geometry generation. For a model to fit a wider population, it needs to respect the mean craniofacial anthropometric values. Therefore, in this work, 12 medical imaging sets from healthy individuals were considered and their craniometry assessed, selecting the case with a higher degree of similarity with the regional mean values. The selected dataset also included the contrast series and the angiographic CT series. This series includes at least 2/3 of the head within the scan, which would help recognize cerebral vessels. The main structures were segmented, and their geometry extracted. It is very important to add that the chosen DICOM (Digital Imaging and Communications in Medicine) set was based only on the MRI (Magnetic Resonance Imaging). Unlike for adults, where CTs are a common clinical approach, the MRI is a preferable medical approach for young children. However, extracting bone structures such as a skull from an MRI is a much more time-consuming procedure compared to the CT-based extraction or a combined MRI-CT approach. At this point, it should be noted that several years of intensive research have not been successful in establishing a generally accepted and undoubtedly functioning segmentation algorithm that could automatically perform an MRI-based task for the brain instances. Therefore, mainly manual methods, as preferred in practice, are still used [77].

In stage II, with the aid of CAD (computer-aided design) tools, CATIA and Meshmixer software, 3D geometries were developed for the skull and brain, including their structural segmentation (e.g., white versus grey matter). These 3D geometries were then imported to a FE software to model the referred head structures (stage III).

In stage III, a mesh-sensitive study is carried out, varying the type of element and their size. Triangular and tetrahedral elements, commonly used in FE head models, are associated with poor performance issues, such as the constant-strain triangle [78,79], which is an issue in head modelling due to the existence of strain gradients. Therefore, there is the necessity of employing quadrilateral and hexahedral elements to eliminate artificial behaviours, which is not an easy task due to the complexity of some intracranial structures, leading meshing algorithms to fail in its generation. In this work, novel algorithms were used for the generation of high-quality, entirely hexahedral meshes, including both soft and hard tissues. The same arguments are valid for fluid modelling, which is usually oversimplified by employing solid tetrahedral or hexahedral elements. The aHEAD model employs fluid–structure interaction (FSI) by smoother particle hydrodynamics (SPH), being able to simulate the CSF (cerebrospinal fluid) flow during an impact, which is not properly done with conventional models with solid elements and simple (n = 1) hyper-elastic material models [80].

Additionally, sub-models were developed to understand the feasibility of the modelling strategy of each component and the constitutive modelling strategy. These sub-models also make it possible to efficiently identify possible modelling issues that would be hard to diagnose in the full model. As already referred, experiments were also carried out in order to identify suitable material models.

The penultimate stage IV was dedicated to the modelling of several intracranial structures of the CNS. This stage demands meticulous actions in order to guarantee precise modelling of intracranial structures, such as the superior sagittal sinus (SSS) and the bridging veins (BV) as well as the falx cerebri and tentorium cerebelli. The final aHEAD 2-year-old child model is depicted in Figure 4.

The final stage V, due to the inexistence of experimental child head impact data for the numerical model validations, consists in a verification stage by simulating several tests where loading conditions, objects and impact regions are varied to impose several impact conditions, such as different degrees of strain rate on the brain tissue.

4.1. Materials and Nomenclature

Analysing publications in the field of head numerical modelling and head biomechanics during road accidents, Global Human Body Models Consortium (GHBMC) and Total Human Model for Safety (THUMS) models are the most popular [81,82]. Even though they are representatives of the group of full-body response models, the grade of details is high concerning their implemented head models. Moreover, unlike other models available in the literature, more recent versions of these models have a division into grey and white matter. Medical cases show that most brain damage occurs at the interface between grey matter and white matter, e.g., diffuse axonal injury. This is because these structures have a different structure, which in turn must affect their mechanical properties.

Due to the fact that currently children’s models presented in the literature do not distinguish between grey and white matter, the authors based their model on the material properties available for global models GHBMC and THUMS as well as Ogden’s model.

The approach of this study is to use the above models of materials for either homogeneous brain structure —i.e., without white/grey matter separation—or inhomogeneous brain structure —i.e., with white (W) and grey (G) matter. Thus, for a homogeneous brain model, the whole brain is modelled by the white matter (W), whereas for an inhomogeneous model, the authors used different parameters for both grey and white matter (W/G).

Therefore, the nomenclature of the materials used in this publication is as follows:

• Hyper-elastic Ogden Rubber is MAT_HYPERELASTIC (W)
• Viscoelastic GHBMC is MAT_VISCOELASTIC 1 (W or W/G)
• Viscoelastic THUMS is MAT_VISCOELASTIC 2 (W or W/G)

The mechanical properties used for this study are tabularized in

Table 4. Mechanical properties of brain tissues from paediatric heads; units: t/mm/s/MPa.

Structure	Reference	Density (t/m3)	Young’s Modulus or Bulk Modulus (MPa)	Other Material Parameters	Type No. of FEs	Image of Structure
White Matter—left/right hemisphere	Fernandes 2017 [83,84] - MAT_HYPERELASTIC	1.04 × 10−9	–	Ν = 0.49999 Mu1 = 0.0012 Alpha1 = 5.05007	hexa 233,760/245,830
	GHBMC [85] MAT_VISCOELASTIC 1	1.06 × 10−9	Bulk modulus 2.19 × 10−3	G0 = 7.5 × 10−3 G1 = 1.5 × 10−3
	THUMS MAT_VISCOELASTIC 2	1.00 × 10−9	Bulk modulus 2.16 × 10−3	G0 = 12.5 × 10−3 G1 = 6.125 × 10−3
Grey matter—left/right hemisphere	Fernandes 2017 [83,84] - MAT_HYPERELASTIC	1.04 × 10−9	–	Ν = 0.49999	hexa 208,498/201,127
	GHBMC [85] MAT_VISCOELASTIC 1	1.06 × 10−9	Bulk modulus 2.19 × 10−3	G0 = 6 × 10−3 G1 = 1.2 × 10−3
	THUMS MAT_VISCOELASTIC 2	1.00 × 10−9	Bulk modulus 2.16× 10−3	G0 = 10 × 10−3 G1 = 5 × 10−3
Cerebellum	Fernandes 2017 [83,84]	1.04 × 10−9	–	Ν = 0.49999 Mu1 = 0.0012 Alpha1 = 5.05007	hexa 128,659
Brainstem	Fernandes 2017 [83,84]	1.04 × 10−9	–	Ν = 0.49999 Mu1 = 0.0012 Alpha1 = 5.05007	hexa 20,981
Pia mater	LLC Elemance 2014; Ratajczak et al. 2019 [72,86]	1.13 × 10−9	31.5	ν = 0.45000	shell 141,831
Dura mater (with falx cerebri and tentorium cerebelli)	LLC Elemance 2014; Ratajczak et al. 2019 [72,86]	1.13 × 10−9	31.5	ν = 0.45000	tri shell 950
					quad shell 25,169
Superior sagittal sinus and transversal sinus	LLC Elemance 2014; Ratajczak et al. 2019 [72,86]	1.04 × 10−9	28.2	ν = 0.45000	tri shell 212
					quad shell 9065
Bridging veins	Delye et al. 2006; LLC Elemance 2014; Monea et al. 2014 [86,87,88]	1.13 × 10−9	30	0.48000	tri shell 410
					quad shell 14,291
Lamina interna	Giordano and Kleiven 2016; Margulies 2000; Ratajczak et al. 2019 [50,72,89,90]	2.1 × 10−9	4 × 103	0.25000	hexa 158,553
Diploe	Giordano and Kleiven 2016; Margulies 2000; Ratajczak et al. 2019 [50,72,90]	1.0 × 10−9	1 × 103	0.30000	hexa 121,436
Lamina externa	Giordano and Kleiven 2016; Margulies 2000; Ratajczak et al. 2019 [50,72,90]	2.1 × 10−9	4 × 103	0.25000	hexa 195,357
Cerebrospinal fluid (CSF)	DYNAmore GmbH 2018; Gomez-Gesteira et al. 2012 [91,92]	1 × 10−9	–	viscosity coefficient 7 × 10−10	SPH 165,289
Corpus callosum	Fernandes 2017 [83,84]	1.04 × 10−9	Same as for WM	Same as for WM	hexa 6452
Third ventricle complex	Fernandes 2017 [83,84]	1.04 × 10−9	Same as for WM	Same as for WM	hexa 762
Liliequist membrane	Fernandes 2017 [83,84]	1.04 × 10−9	28.2	0.45000	tri shell 56
				0.45000	quad shell 189

, whereas are: ν—Poisson’s ratio, G₀—shear modulus, G₁—Long-time (G∞) shear modulus, Mu1—first shear modulus, and alpha-1—first exponent for Ogden Rubber (Hyper-elastic) model material in LS-DYNA code [81].

4.2. Boundary Conditions

The boundary conditions for the simulations were set following Hardy et al. [93], where the measurements were recorded using a 6-axis accelerometer, which registered both linear and angular acceleration. The output data from the accelerometer, with six different acceleration functions in time, was used in the numerical simulations as the input load function applied to the skull’s centre of mass (Figure 5). The geometric and material verifications were carried out based on the correlation with Hardy’s research, which was based on the measurement of the relative displacement of the brain in relation to the skull. The test with the identifier C755-T2 was selected for this research due to the circumstance that it has been widely used in literature for Finite Element Head Models (FEHMs).

In this study, the effect of the selection of the material model on the relative displacement of the brain was investigated. The intracranial motion was compared between homogeneous (just white matter—W) and inhomogeneous brain (different mechanical properties for white and grey matters—W/G). Importantly, all markers (FE nodes) except for a5, are located in the white matter of the brain.

5. Results and Discussion

We commenced five simulations, where the model was subjected to the same acceleration loading in accordance with the C755-T2 test:

▪

2 simulations for MAT_VISCOELASTIC 1 (W and W/G)

▪

2 simulations for MAT_VISCOELASTIC 2 (W and W/G)

▪

1 simulation for MAT_HYPERELASTIC (W), as the data for grey matter is missing in the literature for this model of material.

As the craniocerebral injuries arise as a result of the relative displacement of the brain relative to the skull, we hypothesized that depending on the mechanical properties of the brain tissue, the displacements may be significantly different. In practice, this can change the degree of brain tissue damage. Thus, the study presents to what extent the application of the material model affects the displacement of brain tissue. At the same time, the effect of grey matter and white matter separation in the model on brain displacement is investigated.

The research results showed that depending on the material model used, the brain kinematics are different. This phenomenon can be observed in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11, where displacements as a function of time for different groups of materials is presented.

The obtained results for MAT_VISCOELASTIC 1 showed that taking into account the distinction in the numerical model of white and grey matter may have a significant impact on brain displacement, as shown in Figure 10, which depicts the markers placed in the brain model with only white matter (W) and the brain model with the separation between white and grey matter (W/G). It should be noted that in this simulation, both angular and linear velocities were implied as the mechanical loading. At this point, it should be mentioned that angular acceleration is the main cause of DAI.

Interestingly, for MAT_VISCOELASTIC 2, the W/G matter separation does not significantly influence the kinematics of the 10 selected markers (FE nodes). The overlapping displacement-in-time characteristics for homogeneous and inhomogeneous MAT_VISCOELASTIC 2 are depicted in Figure 11. This issue needs some further research, yet the authors’ hypothesis is that the Kelvin/Maxwell relaxation/decay constant plays a significant role. When the relaxation/decay constant parameter is lower, then tendency for relaxation behaviour in time increment is lower. Therefore, relaxation strain is much lower for both grey and white matter. As a consequence, the strain difference between grey and white matter do not expose such distinction in homogeneous and inhomogeneous MAT_VISCOELASTIC 2 models.

Figure 12 depicts the relative resultant displacement of the brain for the C755-T2 test for the MAT_VISCOELASTIC 1 (W/G) inhomogeneous brain model. We can observe that the most displaced finite elements are located in the brain cortex as they are subjected to the highest angular acceleration. It is worth to notice again that DAI is usually caused by high rotational accelerations, leading to shear loads in the brain tissue [33]. A similar phenomenon is observed for all the considered configurations in this paper.

In all the respective simulations, we can see a noticeable pressure gradient at 10 ms after the loading, i.e., just after the 20 g linear acceleration inducement. The occurrence of brain contusions is associated with pressure gradients, correlated with linear acceleration during a head impact [95]. To a degree, traumatic brain hematoma is in a continuum with brain contusions and cortex lacerations and can be secondary to those lesions in some cases. These lesions are usually seen in orbitofrontal and temporal pole regions. Often, these lesions occur on the opposite area of the brain—so-called contrecoup injuries, often more severe than coup lesions [39]. In Figure 13, the coupe phenomenon is visible in the frontal lobe for all the studied models.

Due to the novel introduction SPH approach as the CSF, we obtained biofidelic interference between the brain and skull without a compromise of the simplifications often seen in the literature, such as node cortex-CSF-skull node sharing. Thus, in the aHEAD model, the particles can flow around the brain and create soft support for brain tissue. This approach allows the authors to simulate proper interaction between the skull and brain, as is depicted in Figure 14.

The paediatric head trauma depends on many factors, such as environment and age. The most common cause of injury among the paediatric population seems to be motor vehicle accidents. Falls tend to be more common among the youngest, up to 5 years old [10,96,97,98,99,100,101]. Head injuries are the most frequent trauma at this age range [96,102] and have the highest impact on adolescence life comparing all age groups followed by injury repetition. After major head trauma, CT scans reveal skull fractures of different magnitudes in over 50% of clinically not silent lesions [103], followed by a similar number of brain concussions and brain edema. Less often, a posttraumatic SDH and EDH are found [103,104]. Due to the difficulty of obtaining CT images from healthy children, the authors only had magnetic resonance images. This fact constitutes a certain difficulty in creating the skull model. The model of the brain divided into segments allows us to accurately characterize the formation of the DAI mechanism and makes it possible to determine the stress distribution at the white matter and grey matter junction. Based on the presented research, the further the tissues are from the skull’s CoG, the bigger the relative displacements are. This effect can be observed for markers a3, a4, a5, p3, p4, and p5 for all considered material models.

In 2013, Bharat K. Soni et al. wrote: “(…) little attention has been paid to detailed modelling of the brain, which lags the complexity of currently published adult brain models. None of the published paediatric head models have utilised different properties to represent grey and white matter, although this distinction has been reported to influence injury prediction in the adult” [21]. Thus, the current approach goes beyond the state-of-the-art in this field. Numerical modelling related to the biomechanics of head injuries can provide a quick and inexpensive way to predict how external mechanical loads affect individual craniocerebral tissues. It should be noted that simulations using the finite element method provide a much more accurate representation of the tissue biomechanics system than multibody simulations. Nevertheless, preparing an accurate model with this level of complexity is significantly labour-intensive and time-consuming. Models need a high level of representation of anatomy, providing paediatric-specific data on head mechanical properties and of the environment of injury. Many of the current models simplify the anatomy, due to the finite element meshing limitations. In that case, a vast propagation of injury energy can be seen, that does not necessarily represent the true nature of the lesion and how the brain reacts to it in real life.

In every research method, there is a question with assessing the reliability of the obtained results. The issue is to determine the mechanical properties of human’s body parts, including the tissues that constitute the analysed anatomical region. Paediatric head models in impact biomechanics can offer useful information to researchers, but it is currently difficult to consider quantitative results from the models due to a lack of rigorous validation. Especially, due to the uncertainty, if the gathered data can refer statistically to a wider group of patients with the same or similar age, or if the data simply represents the underlying patient. It makes the data to a resilient choice of data from a limited set of available real-world cases. What remains is the complex interpretation of numerical results. It helps to reveal injury mechanisms while trying to prove the robustness of the data.

6. Conclusions

The limitation of in vivo studies on the human brain made the finite element modelling an important tool to study head injuries. The numerical modelling might provide additional data about brain injury propagation (occurrence of secondary brain trauma), and therefore have some input to medical practice in the treatment of certain trauma cases. It might point to potential lesions, which are not yet visible in radiological imaging, or not obvious on the initial examination. Compared with the adult FEHM, relatively few studies have been reported for modelling paediatric impact biomechanics. What is more, the degree of anatomical detail has been lagging behind that of the adult models. Scaling down an adult head to obtain a child head in testing should not be used and specific child geometry is needed to investigate child injury mechanisms.

The aHEAD 2yo model of a small child is very advanced in its structure and material compared to the models currently available in the literature. The authors believe this comprehensive work will push the state-of-the-art of paediatric head models. Although validation is limited due to the inherent difficulties of obtaining experimental data, a new high-quality model is presented, and the intracranial motion is assessed. These results will make it possible to further comparisons between future numerical paediatric head models. Thus, the authors believe that this model may serve as the benchmark model as all material data and the model structure have been revealed and referred.

It should be mentioned that in the presented model, the space for cerebrospinal fluid was filled with the smoothed-particle hydrodynamics meshfree method. This approach allows cerebrospinal fluid to have complex dynamics, which was presented in the paper. On the other hand, modelling of local quasi-flow by implementing low shear-modulus by solid elements may inherit a significant, yet not intended, support for the brain within the skull. Nevertheless, the vast majority of FEHMs have set the cerebrospinal fluid as solid finite elements, which may not sufficiently reflect the biomechanics of the tissue. In addition, the aHEAD model consists only of hexahedral elements for 3D structures. However, in order for paediatric FEHMs to realise their full potential, extensive cadaveric or tissue tests need to be performed. Since this is unlikely to occur, mainly due to ethical responses, some new techniques and methods, such as the ones described in this study, must be developed to bridge the gaps in the state-of-the-art.

The study showed that the use of the material model has a significant impact on the biomechanical response of the brain during impact. At the same time, it has been presented that the differentiation of white and grey matter may significantly affect brain displacement under the mechanical loading. It can be interpreted that the model divided into grey and white matter more accurately reflects the brain response in the real world compared to the unsegmented model. As a result, the biomechanics of destruction in the interface of grey/white matter can be better investigated. It should be noted that material models should be improved by conducting further experimental research on children’s tissues. In particular, we still know very little about how the material characteristics change during brain development. During this period, the mechanical properties and tissue proportions including grey matter to white matter can change significantly. It is important to emphasize that currently, there is a lack of data for validation of children’s head models. To date, the current validation of numerical models consists mainly of comparing acceleration and deflection force diagrams for fall and compression tests.

Overall, the numerical biomechanics research has made a significant contribution to understanding the mechanisms and tolerances of adult traumatic brain injury, and it continues to play a crucial role in forming guidelines for adult motor vehicle occupancy, sports safety, and other fields where TBI or DAI might occur.