Conventional Soliton and Noise-Like Pulse Generated in an Er-Doped Fiber Laser with Carbon Nanotube Saturable Absorbers
Abstract
:Featured Application
Abstract
1. Introduction
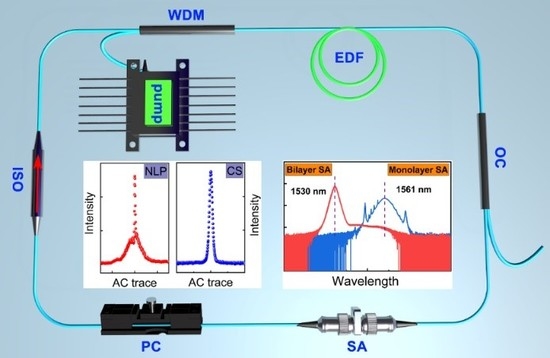
2. Experimental Results
3. Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Malinauskas, M.; Zukauskas, A.; Hasegawa, S.; Hayasaki, Y.; Mizeikis, V.; Buividas, R.; Juodkazis, S. Ultrafast laser processing of materials: From science to industry. Light Sci. Appl. 2016, 5, e16133. [Google Scholar] [CrossRef] [Green Version]
- Fermann, M.E.; Hartl, I. Ultrafast fibre lasers. Nat. Photonics 2013, 7, 868–874. [Google Scholar] [CrossRef]
- Liu, X.; Guo, Q.; Qiu, D.J. Emerging Low-Dimensional Materials for Nonlinear Optics and Ultrafast Photonics. Adv. Mater. 2017, 29, 1605886. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Kutz, J.N. Mode-Locked Soliton Lasers. SIAM Rev. 2006, 48, 629–678. [Google Scholar] [CrossRef]
- Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Jeong, Y.; Vazquez-Zuniga, L.A.; Lee, S.; Kwon, Y. On the formation of noise-like pulses in fiber ring cavity configurations. Opt. Fiber Technol. 2014, 20, 575–592. [Google Scholar] [CrossRef]
- Li, L.; Pang, L.; Zhao, Q.; Liu, W.; Su, Y. VSe2 nanosheets for ultrafast fiber lasers. J. Mater. Chem. C 2020, 8, 1104–1109. [Google Scholar] [CrossRef]
- Li, L.; Pang, L.; Zhao, Q.; Wang, Y.; Liu, W. Niobium disulfide as a new saturable absorber for an ultrafast fiber laser. Nanoscale 2020, 12, 4537–4543. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wu, Q.; Zhang, F.; Chen, L.; Jin, X.; Hu, Y.; Zheng, Z.; Zhang, H. 2D Black Phosphorus Saturable Absorbers for Ultrafast Photonics. Adv. Opt. Mater. 2019, 7, 1800224. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Liu, J.; Wang, C.; Yang, K.; Lee, C.; Zhang, H.; He, J. Recent Progress in 2D Material-Based Saturable Absorbers for All Solid-State Pulsed Bulk Lasers. Laser Photonics Rev. 2019, 14, 1900240. [Google Scholar] [CrossRef]
- Guo, B.; Xiao, Q.L.; Wang, S.H.; Zhang, H. 2D Layered Materials: Synthesis, Nonlinear Optical Properties, and Device Applications. Laser Photonics Rev. 2019, 13, 1800327. [Google Scholar] [CrossRef]
- Hasegawa, A. Soliton-Based Optical Communications: An Overview. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 1161–1172. [Google Scholar] [CrossRef]
- Xia, H.; Li, H.; Deng, G.; Li, J.; Zhang, S.; Liu, Y. Compact noise-like pulse fiber laser and its application for supercontinuum generation in highly nonlinear fiber. Appl. Opt. 2015, 54, 9379–9384. [Google Scholar] [CrossRef]
- Grelu, W.C.P.; Ankiewicz, A.; Soto-Crespo, J.M.; Akhmediev, N. Dissipative soliton resonance as a guideline for high-energy pulse laser oscillators. J. Opt. Soc. Am. B 2010, 27, 2336–2341. [Google Scholar] [CrossRef] [Green Version]
- Marini, A.; Cox, J.D.; de Abajo, F.J.G. Theory of graphene saturable absorption. Phys. Rev. B 2017, 95, 125408. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Haus, J.W. Fiber-based saturable-absorber action based on a focusing Kerr effect. Opt. Commun. 2016, 367, 292–298. [Google Scholar] [CrossRef]
- Xu, H.; Wan, X.; Ruan, Q.; Yang, R.; Du, T.; Chen, N.; Cai, Z.; Luo, Z. Effects of Nanomaterial Saturable Absorption on Passively Mode-Locked Fiber Lasers in an Anomalous Dispersion Regime: Simulations and Experiments. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1100209. [Google Scholar] [CrossRef]
- Du, W.; Li, H.; Li, J.; Wang, P.; Zhang, S.; Liu, Y. Mechanism of dissipative-soliton-resonance generation in fiber laser mode-locked by real saturable absorber. Opt. Express 2018, 26, 21314–21323. [Google Scholar] [CrossRef]
- Bao, Q.; Zhang, H.; Wang, Y.; Ni, Z.; Yan, Y.; Shen, Z.X.; Loh, K.P.; Tang, D.Y. Atomic-Layer Graphene as a Saturable Absorber for Ultrafast Pulsed Lasers. Adv. Funct. Mater. 2009, 19, 3077–3083. [Google Scholar] [CrossRef]
- Zhang, J.; Ouyang, H.; Zheng, X.; You, J.; Chen, R.; Zhou, T.; Sui, Y.; Liu, Y.; Cheng, X.; Jiang, T. Ultrafast saturable absorption of MoS2 nanosheets under different pulse-width excitation conditions. Opt. Lett. 2018, 43, 243–246. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Chen, T.; Li, M.; Zhang, B.; Lu, Y.; Chen, K.P. All-fiber ultrafast thulium-doped fiber ring laser with dissipative soliton and noise-like output in normal dispersion by single-wall carbon nanotubes. Appl. Phys. Lett. 2013, 103, 011103. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Hasan, T.; Ferrari, A.C. Ultrafast lasers mode-locked by nanotubes and graphene. Physica E 2012, 44, 1082–1091. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, H.; Qi, X.; Chen, Y.; Wang, Z.; Wen, S.; Tang, D. Ultra-short pulse generation by a topological insulator based saturable absorber. Appl. Phys. Lett. 2012, 101, 211106. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, G.; Chen, S.; Guo, Z.; Yu, X.; Zhao, C.; Zhang, H.; Bao, Q.; Wen, S.; Tang, D.; et al. Mechanically exfoliated black phosphorus as a new saturable absorber for both Q-switching and Mode-locking laser operation. Opt. Express 2015, 23, 12823–12833. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, K.; Wang, J.; Fan, J.; Lotya, M.; O’Neill, A.; Fox, D.; Feng, Y.; Zhang, X.; Jiang, B.; Zhao, Q.; et al. Ultrafast Saturable Absorption of Two-Dimensional MoS2 Nanosheets. ACS Nano 2013, 7, 9260–9267. [Google Scholar] [CrossRef]
- Liu, H.; Luo, A.P.; Wang, F.Z.; Tang, R.; Liu, M.; Luo, Z.C.; Xu, W.C.; Zhao, C.J.; Zhang, H. Femtosecond pulse erbium-doped fiber laser by a few-layer MoS2 saturable absorber. Opt. Lett. 2014, 39, 4591–4594. [Google Scholar] [CrossRef]
- Chai, T.; Li, X.; Feng, T.; Guo, P.; Song, Y.; Chen, Y.; Zhang, H. Few-layer bismuthene for ultrashort pulse generation in a dissipative system based on an evanescent field. Nanoscale 2018, 10, 17617–17622. [Google Scholar] [CrossRef]
- Jhon, Y.I.; Koo, J.; Anasori, B.; Seo, M.; Lee, J.H.; Gogotsi, Y.; Jhon, Y.M. Metallic MXene Saturable Absorber for Femtosecond Mode-Locked Lasers. Adv. Mater. 2017, 29, 1702496. [Google Scholar] [CrossRef]
- Vivien, L.; Lancon, P.; Riehl, D.; Hache, F.; Anglaret, E. Carbon nanotubes for optical limiting. Carbon 2002, 40, 9. [Google Scholar] [CrossRef]
- Izard, N.; Ménard, C.; Riehl, D.; Doris, E.; Mioskowski, C.; Anglaret, E. Combination of carbon nanotubes and two-photon absorbers for broadband optical limiting. Chem. Phys. Lett. 2004, 391, 124–128. [Google Scholar] [CrossRef] [Green Version]
- Mao, D.; Du, B.; Yang, D.; Zhang, S.; Wang, Y.; Zhang, W.; She, X.; Cheng, H.; Zeng, H.; Zhao, J. Nonlinear Saturable Absorption of Liquid-Exfoliated Molybdenum/Tungsten Ditelluride Nanosheets. Small 2016, 12, 1489–1497. [Google Scholar] [CrossRef] [PubMed]
- Mao, D.; She, X.; Du, B.; Yang, D.; Zhang, W.; Song, K.; Cui, X.; Jiang, B.; Peng, T.; Zhao, J. Erbium-doped fiber laser passively mode locked with few-layer WSe2/MoSe2 nanosheets. Sci. Rep. 2016, 6, 23583. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.; Lédée, F.; Park, J.; Song, S.; Lee, H.; Lee, Y.S.; Kim, B.; Yeom, D.I.; Deleporte, E.; Oh, K. Mode-Locking of All-Fiber Lasers Operating at Both Anomalous and Normal Dispersion Regimes in the C- and L-Bands Using Thin Film of 2D Perovskite Crystallites. Laser Photonics Rev. 2018, 12, 1800118. [Google Scholar] [CrossRef]
- Xiao, P.; Wu, K.; Mao, D.; Chen, J. A pulsewidth measurement technology based on carbon-nanotube saturable absorber. Opt. Express 2019, 27, 4188–4203. [Google Scholar] [CrossRef]
- Dong, Z.K.; Xu, R.Q.; Zhang, W.H.; Guoyu, H.Y.; Hua, L.L.; Tian, J.R.; Song, Y.R. Er-doped all-fiber laser mode-locked by graphitic carbon nitride nanosheets. Chin. Opt. Lett. 2018, 16, 081402. [Google Scholar] [CrossRef] [Green Version]
- Dennis, M.L.; Duling, I.N. Experimental Study of Sideband Generation in Femtosecond Fiber Lasers. IEEE J. Quantum Electron. 1994, 30, 1469–1477. [Google Scholar] [CrossRef]
- Malinauskas, M.; Žukauskas, A.; Hasegawa, S.; Hayasaki, Y.; Mizeikis, V.; Buividas, R.; Juodkazis, S. “Effect of frequency chirp on soliton spectral sidebands in fiber lasers. Opt. Lett. 1995, 20, 1286–1288. [Google Scholar]













| WDM | EDF | SMF | OC | SA |
|---|---|---|---|---|
| β2 = 4.5 ps2/km | β2 = 15.54 ps2/km | β2 = −12.2 ps2/km | 10% output | = 15% |
| Γ = 1.1 × 10−3 m−1W−1 | Γ = 3.0 × 10−3 m−1W−1 | Γ = 3.0 × 10− 3 m−1W−1 | i.e., T = 90% | = * |
| LWDM = 0.5 m | LEDF = 0.5 m | LSMF1 = 0.5 m | Isat = * | |
| Ωg = 40 nm | LSMF2 = 0.5 m | Β = * | ||
| g0 = * | LSMF3 = 4.5 m | |||
| Psat,g = 2.3 W |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Tian, J.; Li, R.; Cui, Y.; Zhang, W.; Song, Y. Conventional Soliton and Noise-Like Pulse Generated in an Er-Doped Fiber Laser with Carbon Nanotube Saturable Absorbers. Appl. Sci. 2020, 10, 5536. https://doi.org/10.3390/app10165536
Dong Z, Tian J, Li R, Cui Y, Zhang W, Song Y. Conventional Soliton and Noise-Like Pulse Generated in an Er-Doped Fiber Laser with Carbon Nanotube Saturable Absorbers. Applied Sciences. 2020; 10(16):5536. https://doi.org/10.3390/app10165536
Chicago/Turabian StyleDong, Zikai, Jinrong Tian, Runlai Li, Youshuo Cui, Wenhai Zhang, and Yanrong Song. 2020. "Conventional Soliton and Noise-Like Pulse Generated in an Er-Doped Fiber Laser with Carbon Nanotube Saturable Absorbers" Applied Sciences 10, no. 16: 5536. https://doi.org/10.3390/app10165536
APA StyleDong, Z., Tian, J., Li, R., Cui, Y., Zhang, W., & Song, Y. (2020). Conventional Soliton and Noise-Like Pulse Generated in an Er-Doped Fiber Laser with Carbon Nanotube Saturable Absorbers. Applied Sciences, 10(16), 5536. https://doi.org/10.3390/app10165536