Thermodynamic Efficiency of Water Vapor/Solid Chemical Sorption Heat Storage for Buildings: Theoretical Limits and Integration Considerations
Abstract
:Featured Application
Abstract
1. Introduction
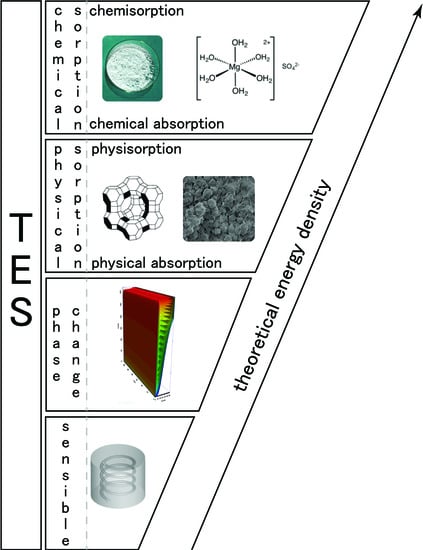
2. Heat Storage Classification
- Absorption is the process of one material (absorbate) being retained by another (absorbent); this may be the physical solution of a gas, liquid, or solid in a liquid, attachment of molecules of a gas, vapor, liquid, or dissolved substance to a solid surface by physical forces, etc..
- Adsorption is an increase in the concentration of a dissolved substance at the interface of a condensed and a liquid phase due to the operation of surface forces. Adsorption can also occur at the interface of a condensed and a gaseous phase.
- Chemical absorption or reactive absorption is a chemical reaction between the absorbed and the absorbing substances. Sometimes it combines with physical absorption. This type of absorption depends upon the stoichiometry of the reaction and the concentration of its reactants.
- Chemical adsorption is called chemisorption. Chemisorption is Adsorption which results from chemical bond formation (strong interaction) between the adsorbent and the adsorbate in a monolayer on the surface [20].
3. Basics of Chemical Thermodynamics
3.1. Energy Change in Chemical Sorption
3.2. Enthalpy of Reaction
4. Material Considerations
| Hydrated Salt | Dehydrated Salt | [kJ mol−1] | [kJ mol−1] | Reference |
|---|---|---|---|---|
| MgSO4·6H2O | MgSO4·H2O | 275.7 | 55.1 | [26] |
| LiNO3·3H2O | LiNO3 | 165.8 | 55.3 | [27] |
| Al2(SO4)3·18H2O | Al2(SO4)3·8H2O | 554.5 | 55.4 | [27] |
| CaCl2·6H2O | CaCl2·H2O | 277.0 | 55.4 | [27] |
| CuSO4·5H2O | CuSO4·3H2O | 111.7 | 55.8 | [26] |
| SrCl2·6H2O | SrCl2 | 342.0 | 57.0 | [27] |
| LiSO4·H2O | LiSO4 | 57.2 | 57.2 | [26] |
| CuSO4·3H2O | CuSO4·H2O | 114.8 | 57.4 | [26] |
| La(NO3)3·6H2O | La(NO3)3·1·5H2O | 260.4 | 57.9 | [27] |
| MgCl2·6H2O | MgCl2·4H2O | 116.4 | 58.2 | [26] |
| LaCl3·7H2O | LaCl3·H2O | 355.5 | 59.3 | [27] |
| Na2S2O3·5H2O | Na2S2O3 | 279.9 | 56.0 | [27] |
| MgSO4·7H2O | MgSO4·H2O | 335.7 | 56.0 | [27] |
| CaCl2·2H2O | CaCl2·0·3H2O | 101.0 | 59.4 | [28] |
| MgCl2·6H2O | MgCl2 | 361.2 | 60.2 | [29] |
| KOH·2H2O | KOH·1·2H2O | 48.2 | 60.3 | [27] |
| Zn(NO3)2·6H2O | Zn(NO3)2 | 372.0 | 62.0 | [27] |
| Na2S·5H2O | Na2S | 310.0 | 62.0 | [30] |
| CaBr2·6H2O | CaBr2·0·3H2O | 353.9 | 62.1 | [27] |
| LiCl·H2O | LiCl | 62.2 | 62.2 | [27] |
| K2CO3·1·5H2O | K2CO3 | 95.5 | 63.7 | [27] |
| SrBr2·6H2O | SrBr2·H2O | 337.0 | 67.4 | [27] |
| MgCl2·4H2O | MgCl2·2H2O | 135.6 | 67.8 | [26] |
5. Efficiency: From Material to System
5.1. Concepts
5.2. Literature Review
5.2.1. Closed Systems
5.2.2. Open Systems
5.3. Discussion
6. Thermodynamic Efficiency: From System to Integration in Buildings
- ○
- Heat losses in the system are not taken into account.
- ○
- Sensible heat of materials and parts of the reactor are neglected.
- ○
- The energy released or absorbed by the reaction is approximated by the standard enthalpy of reaction.
- ○
- The equilibrium drop influence is neglected (see [18]).
- ○
- Only total hydration/dehydration processes are under investigation.
7. Conclusions
- Energy required for evaporation of water is, at least, 65% of the available energy of reaction.
- For a perfect system, the maximum theoretical energy efficiency of the system is about 1.8.
- Developing water evaporation system “energy–free” or low–energy for the discharging phase.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| List of Symbols | ||
| C | specific heat capacity | J kg−1 K−1 |
| H | enthalpy | J |
| vaporization heat of water | J kg−1 | |
| P | pressure | Pa |
| Q | heat energy per mole of salt | Jmol−1 |
| R | gas constant | J K−1 mol−1 |
| S | entropy | J |
| T | temperature | K |
| U | internal energy | J |
| V | volume | m3 |
| W | work | J |
| Greek letters | ||
| stoechiometric coefficient | ||
| efficiency | ||
| advancement of reaction | ||
| Subscript | ||
| e | equilibrium | |
| evaporation | ||
| maximum | ||
| minimum | ||
| r | reaction | |
| 0 | standard | |
| Superscript | ||
| 0 | standard | |
| − | recovered energy | |
| + | supplied energy | |
References
- Kuznik, F.; Johannes, K.; Obrecht, C. Chemisorption heat storage in buildings: State–of–the–art and outlook. Energy Build. 2015, 106, 183–191. [Google Scholar] [CrossRef]
- Prieto, C.; Cooper, P.; Fernandez, A.I.; Cabeza, L. Review of technology: Thermochemical energy storage for concentrated solar power plants. Renew. Sustain. Energy Rev. 2016, 60, 909–929. [Google Scholar] [CrossRef] [Green Version]
- Sole, A.; Martorell, I.; Cabeza, L. State of the art on gas–solid thermochemical energy storage systems and reactors for building applications. Renew. Sustain. Energy Rev. 2015, 47, 386–398. [Google Scholar] [CrossRef] [Green Version]
- Cot-Gores, J.; Castell, A.; Cabeza, L. Thermochemical energy storage and conversion: A–state–of–the–art review of the experimental research under practical conditions. Renew. Sustain. Energy Rev. 2012, 16, 5207–5224. [Google Scholar] [CrossRef]
- Andre, L.; Abanades, S.; Flamant, G. Screening of thermochemical systems based on solid-gas reversible reactions for high temperature solar thermal energy storage. Renew. Sustain. Energy Rev. 2016, 64, 703–715. [Google Scholar] [CrossRef]
- Aydin, D.; Casey, S.P.; Riffat, S. The latest advancements on thermochemical heat storage systems. Renew. Sustain. Energy Rev. 2015, 41, 356–367. [Google Scholar] [CrossRef]
- Cabeza, L.; Sole, A.; Barreneche, C. Review on sorption materials and technologies for heat pumps and thermal energy storage. Renew. Energy 2017, 110, 3–39. [Google Scholar] [CrossRef] [Green Version]
- Kuznik, F. Chemisorption heat storage for solar low-energy buildings. In Advances in Solar Heating and Cooling; Wang, R.Z., Ge, T.S., Eds.; Woodhead Publishing: Cambridge, UK, 2016; pp. 467–487. [Google Scholar]
- Dincer, I.; Rosen, M. Thermal Energy Storage: Systems and Applications; Wiley: Hoboken, NJ, USA, 2010; 620p. [Google Scholar]
- Zondag, H.; Rikkert, B.; Smeding, S.; de Boer, R.; Bakker, M. Prototype thermochemical heat storage with open reactor system. Appl. Energy 2013, 109, 360–365. [Google Scholar] [CrossRef]
- Fopah-Lele, A.; Rohde, C.; Neumann, K.; Tiejen, T.; Ronnebeck, T.; N’Tsoukpoe, K.E.; Osterl, T.; Opel, O.; Ruck, W.K. Lab-scale experiment of a closed thermochemical heat storage system including honeycomb heat exchanger. Energy 2016, 114, 225–238. [Google Scholar] [CrossRef]
- Mauran, S.; Lahmidi, H.; Goetz, V. Solar heating and cooling by a thermochemical process. First experiments of a prototype storing 60 kW h by a solid/gas reaction. Sol. Energy 2008, 82, 623–636. [Google Scholar] [CrossRef]
- De Jong, A.J.; van Vliet, L.; Hoegaerts, C.; Roel, S.M.; Cuypers, R. Thermochemical Heat Storage—From Reaction Storage Density to System Storage Density. Energy Proc. 2016, 91, 128–137. [Google Scholar] [CrossRef] [Green Version]
- Michel, B.; Mazet, N.; Neveu, P. Experimental investigation of an open thermochemical process operating with a hydrate salt for thermal storage of solar energy: Local reactive bed evolution. Appl. Energy 2016, 180, 234–244. [Google Scholar] [CrossRef]
- Michel, B.; Mazet, N.; Neveu, P. Experimental investigation of an innovative thermochemical process operating with a hydrate salt and moist air for thermal storage of solar energy: Global performance. Appl. Energy 2014, 129, 177–186. [Google Scholar] [CrossRef] [Green Version]
- Richter, M.; Bouche, M.; Linder, M. Heat transformation based on CaCl2/H2O—Part A: Closed operation principle. Appl. Therm. Eng. 2016, 102, 615–621. [Google Scholar] [CrossRef] [Green Version]
- Bouche, M.; Richter, M.; Linder, M. Heat transformation based on CaCl2/H2O—Part B: Open operation principle. Appl. Therm. Eng. 2016, 102, 641–647. [Google Scholar] [CrossRef] [Green Version]
- Obermeier, J.; Muller, K.; Arlt, W. Thermodynamic analysis of chemical heat pumps. Energy 2015, 88, 489–496. [Google Scholar] [CrossRef]
- N’Tsoukpoe, K.E.; Liu, H.; Le Pierres, N.; Luo, L. A review on long-term sorption solar energy storage. Renew. Sustain. Energy Rev. 2009, 13, 2385–2396. [Google Scholar] [CrossRef]
- McNaught, A.D.; Wilkinson, A. IUPAC Compendium of Chemical Terminology, 2nd ed.; Wiley Blackwell: Hoboken, NJ, USA, 1997. [Google Scholar]
- Valdivieso, F.; Bouineau, V.; Pijolat, M.; Soustelle, M. Kinetic study of the dehydration of lithium sulphate monohydrate. Renew. Solid State Ion. 1997, 101–103, 1299–1303. [Google Scholar] [CrossRef]
- Bolis, V. Fundamentals in Adsorption at the Solid-Gas Interface. Concepts and Thermodynamics. In Calorimetry and Thermal Methods in Catalysis; Auroux, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3–50. [Google Scholar]
- Gottfried, J.M. CO Oxidation Over Gold. Ph.D. Thesis, Freien Universitat Berlin, Berlin, Germany, 2003. [Google Scholar]
- Grindstaff, W.K.; Fogel, N. Thermochemistry of cobalt(II) chloride hydrates. J. Chem. Soc. Dalton Trans. 1972, 1476–1481. [Google Scholar] [CrossRef]
- Mishra, S.K.; Kanungo, S.B. Thermal dehydration and decomposition of nickel chloride hydrate NiCl2·H2O. J. Therm. Anal. 1992, 38, 2417–2436. [Google Scholar] [CrossRef]
- Ferchaud, C.J.; Zondag, H.A.; de Boer, R.; Rindt, C. Characterization of the sorption process in thermochemical materials for seasonal solar heat storage application. In Proceedings of the 12th International Conference on Energy Storage, Lleida, Spain, 16–18 May 2012. [Google Scholar]
- N’Tsoukpoe, K.E.; Schmidt, T.; Rammelberger, H.U.; Watts, B.A.; Rick, W.K. A systematic multi–step screening of numerous salt hydrates for low temperature thermochemical energy storage. Appl. Energy 2014, 124, 1–16. [Google Scholar] [CrossRef]
- Molenda, M.; Stengler, J.; Linder, M. Reversible hydration behavior of CaCl2 at high H2O partial pressures for thermochemical energy storage. Thermochim. Acta 2013, 560, 76–81. [Google Scholar] [CrossRef]
- Fopah-Lele, A.; Kuznik, F.; Rammelberger, H.U.; Schmidt, T.; Ruck, W.K. Thermal decomposition kinetic of salt hydrates for heat storage systems. Appl. Energy 2015, 154, 447–458. [Google Scholar] [CrossRef]
- De Boer, R.; Haije, W.; Veldhuis, J. Determination of structural, thermodynamic and phase properties in the Na2S–H2O system for application in a chemical heat pump. Thermochim. Acta 2002, 395, 3–19. [Google Scholar] [CrossRef]
- Iammak, K.; Wongsuwan, W.; Kiatsiroroi, W. Investigation of Modular Chemical Energy Storage Performance. In Proceedings of the Joint International Conference on Sustainable Energy and Environment, Hua Hin, Thailand, 1–3 December 2004; pp. 504–507. [Google Scholar]
- Michel, B.; Mazet, N.; Mauran, S.; Stitou, D. Thermochemical process for seasonal storage of solar energy: Characterization and modeling of a high density reactive bed. Energy 2012, 47, 553–563. [Google Scholar] [CrossRef] [Green Version]
- Marias, F.; Tanguy, G.; Wyttenbach, J.; Rouge, S.; Papillon, P. Thermochemical storage: First results of pilot storage with moist air. In Proceedings of the ISES 2011, Kassel, Germany, 28 August–2 September 2011. [Google Scholar]
- Hongois, S.; Kuznik, F.; Steven, P.; Roux, J.J. Development and characterisation of a new MgSO4/zeolite composite for long-term thermal energy storage. Sol. Energy Mater. Sol. Cells 2011, 95, 1831–1837. [Google Scholar] [CrossRef]
- Li, T.; Wu, S.; Yan, T.; Xu, J.; Wang, R. A novel solid-gas thermochemical multilevel sorption thermal battery for cascaded solar thermal energy storage. Appl. Energy 2016, 161, 1–10. [Google Scholar] [CrossRef]
- N’Tsoukpoe, K.E.; Mazet, N.; Neveu, P. The concept of cascade thermochemical storage based on multimaterial system for household applications. Renew. Energy 2016, 129, 138–149. [Google Scholar]









© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuznik, F.; Johannes, K. Thermodynamic Efficiency of Water Vapor/Solid Chemical Sorption Heat Storage for Buildings: Theoretical Limits and Integration Considerations. Appl. Sci. 2020, 10, 489. https://doi.org/10.3390/app10020489
Kuznik F, Johannes K. Thermodynamic Efficiency of Water Vapor/Solid Chemical Sorption Heat Storage for Buildings: Theoretical Limits and Integration Considerations. Applied Sciences. 2020; 10(2):489. https://doi.org/10.3390/app10020489
Chicago/Turabian StyleKuznik, Frédéric, and Kévyn Johannes. 2020. "Thermodynamic Efficiency of Water Vapor/Solid Chemical Sorption Heat Storage for Buildings: Theoretical Limits and Integration Considerations" Applied Sciences 10, no. 2: 489. https://doi.org/10.3390/app10020489
APA StyleKuznik, F., & Johannes, K. (2020). Thermodynamic Efficiency of Water Vapor/Solid Chemical Sorption Heat Storage for Buildings: Theoretical Limits and Integration Considerations. Applied Sciences, 10(2), 489. https://doi.org/10.3390/app10020489