Enhancing the Prediction Accuracy of Data-Driven Models for Monthly Streamflow in Urmia Lake Basin Based upon the Autoregressive Conditionally Heteroskedastic Time-Series Model
Abstract
:1. Introduction
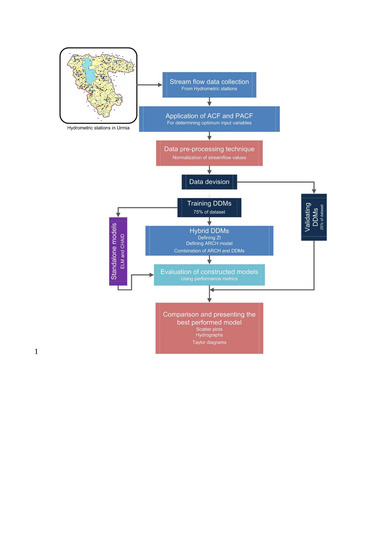
2. Material and Methods
2.1. Study Area and Data Analysis
2.2. ARCH-Type Models
2.3. CHAID Model
2.4. OPELM Model
2.5. Hybrid Models Development
2.6. Optimum Antecedent Streamflow as the Input Variables
2.7. Performance Metrics
3. Application Results
3.1. The Results of the Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF)
3.2. Data Preprocessing
3.3. Application Results of Standalone Models
3.4. ARCH Model
3.5. Results for the Integration of OPELM, CHAID and ARCH Models
3.6. Comparison of Standalone and Hybrid Models
3.7. Discussion
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Modarres, R.; Ouarda, T.B.G. Modelling heteroscedasticty of streamflow time series. Hydrol. Sci. J. 2013, 58. [Google Scholar] [CrossRef]
- Li, F.-F.; Wang, Z.-Y.; Qiu, J. Long-term streamflow forecasting using artificial neural network based on pre-processing technique. J. Forecast. 2018, 38. [Google Scholar] [CrossRef]
- Leigh, C.; Kandanaarachchi, S.; Mcgree, J.M.; Rob, J.; Alsibai, O.; Mengersen, K.; Peterson, E.E. Predicting Sediment and Nutrient Concentrations in Rivers Using High Frequency Water Quality Surrogates. arXiv 2019, arXiv:1810.12499. [Google Scholar]
- Tiwari, M.K.; Chatterjee, C. Development of an accurate and reliable hourly flood forecasting model using wavelet-bootstrap-ANN (WBANN) hybrid approach. J. Hydrol. 2010, 394, 458–470. [Google Scholar] [CrossRef]
- Rezaie-Balf, M.; Kisi, O. New formulation for forecasting streamflow: Evolutionary polynomial regression vs. extreme learning machine. Hydrol. Res. 2017, nh2017283. [Google Scholar] [CrossRef] [Green Version]
- Pappenberger, F.; Beven, K.J.; Hunter, N.M.; Bates, P.D.; Gouweleeuw, B.T.; Thielen, J.; de Roo, A.P.J. Cascading model uncertainty from medium range weather forecasts (10 days) through a rainfall-runoff model to flood inundation predictions within the European Flood Forecasting System (EFFS). Hydrol. Earth Syst. Sci. 2005, 9, 381–393. [Google Scholar] [CrossRef] [Green Version]
- Andersson, J.C.M.; Ali, A.; Arheimer, B.; Gustafsson, D.; Minoungou, B. Providing peak river flow statistics and forecasting in the Niger River basin. Phys. Chem. Earth Parts A/B/C 2017, 100, 3–12. [Google Scholar] [CrossRef]
- Chen, C.S.; Liu, C.-H.; Su, H.-C. A nonlinear time series analysis using two-stage genetic algorithms for streamflow forecasting. Hydrol. Process. 2008, 22, 3697–3711. [Google Scholar] [CrossRef]
- Kalteh, A.M. Monthly river flow forecasting using artificial neural network and support vector regression models coupled with wavelet transform. Comput. Geosci. 2013, 54, 1–8. [Google Scholar] [CrossRef]
- Atiya, A.F.; El-Shoura, S.M.; Shaheen, S.I.; El-Sherif, M.S. A comparison between neural-network forecasting techniques—Case study: River flow forecasting. IEEE Trans. Neural Netw. 1999, 10, 402–409. [Google Scholar] [CrossRef]
- Solgi, A.; Zarei, H.; Nourani, V.; Bahmani, R. A new approach to flow simulation using hybrid models. Appl. Water Sci. 2017, 16, 3691–3706. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Zhang, X.; Qin, H. A data-driven model based on Fourier transform and support vector regression for monthly reservoir inflow forecasting. J. Hydro-Environ. Res. 2018, 18, 12–24. [Google Scholar] [CrossRef]
- Zhu, S.; Heddam, S. Modelling of Maximum Daily Water Temperature for Streams: Optimally Pruned Extreme Learning Machine (OPELM) versus Radial Basis Function Neural Networks (RBFNN). Environ. Process. 2019, 6, 789–804. [Google Scholar] [CrossRef]
- Heddam, S. Use of Optimally Pruned Extreme Learning Machine (OP-ELM) in Forecasting Dissolved Oxygen Concentration (DO) Several Hours in Advance: A Case Study from the Klamath River, Oregon, USA. Environ. Process. 2016, 3, 909–937. [Google Scholar] [CrossRef]
- Hu, J.; Liu, B.; Peng, S. Forecasting salinity time series using RF and ELM approaches coupled with decomposition techniques. Stoch. Environ. Res. Risk Assess. 2019, 33, 1117–1135. [Google Scholar] [CrossRef]
- Yadav, B.; Ch, S.; Mathur, S.; Adamowski, J. Discharge forecasting using an Online Sequential Extreme Learning Machine (OS-ELM) model: A case study in Neckar River, Germany. Measurement 2016, 92, 433–445. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Jaafar, O.; Deo, R.C.; Kisi, O.; Adamowski, J.; Quilty, J.; El-Shafie, A. Stream-flow forecasting using extreme learning machines: A case study in a semi-arid region in Iraq. J. Hydrol. 2016, 542, 603–614. [Google Scholar] [CrossRef]
- Adamala, S. Time Series Analysis: A Hydrological Prospective. Am. J. Sci. Res. Essays Am. J. Sci. Res. Essays Res. Artic. AJSRE 2016, 1, 0031–0040. [Google Scholar] [CrossRef] [Green Version]
- Hinich, M.J. Testing for gaussianity and linearity of a stationary time series. J. Time Ser. Anal. 1982, 3, 169–176. [Google Scholar] [CrossRef]
- Wang, W.; Vrijling, J.K.; Van Gelder, P.H.A.J.M.; Ma, J. Testing for nonlinearity of streamflow processes at different timescales. J. Hydrol. 2006, 322, 247–268. [Google Scholar] [CrossRef]
- Alkhasawneh, M.S.; Ngah, U.K.; Tay, L.T.; Mat Isa, N.A.; Al-Batah, M.S. Modeling and Testing Landslide Hazard Using Decision Tree. J. Appl. Math. 2014, 2014, 929768. [Google Scholar] [CrossRef] [Green Version]
- Althuwaynee, O.F.; Pradhan, B.; Lee, S. A novel integrated model for assessing landslide susceptibility mapping using CHAID and AHP pair-wise comparison. Int. J. Remote Sens. 2016, 37, 1190–1209. [Google Scholar] [CrossRef]
- Salas, J.D.; Tabios, G.Q.; Bartolini, P. Approaches to multivariate modeling of water resources time series. J. Am. Water Resour. Assoc. 1985, 21, 683–708. [Google Scholar] [CrossRef]
- Castellano-Méndez, M.; González-Manteiga, W.; Febrero-Bande, M.; Manuel Prada-Sánchez, J.; Lozano-Calderón, R. Modelling of the monthly and daily behaviour of the runoff of the Xallas river using Box–Jenkins and neural networks methods. J. Hydrol. 2004, 296, 38–58. [Google Scholar] [CrossRef]
- Quintela-del-Río, A.; Francisco-Fernández, M. River flow modelling using nonparametric functional data analysis. J. Flood Risk Manag. 2018, 11, S902–S915. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. The Use of Artificial Neural Networks for the Prediction of Water Quality Parameters. Water Resour. Res. 1996, 32, 1013–1022. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Freire, P.K.M.M.; da Silva, R.M.; Akrami, S.A. Hybrid Wavelet Neural Network Approach for Daily Inflow Forecasting Using Tropical Rainfall Measuring Mission Data. J. Hydrol. Eng. 2019, 24, 04018062. [Google Scholar] [CrossRef]
- Astel, A.; Mazerski, J.; Polkowska, Z.; Namieśsnik, J. Application of PCA and time series analysis in studies of precipitation in Tricity (Poland). Adv. Environ. Res. 2004, 8, 337–349. [Google Scholar] [CrossRef]
- Machiwal, D.; Jha, M.K. Comparative evaluation of statistical tests for time series analysis: Application to hydrological time series. Hydrol. Sci. J. 2008, 53, 353–366. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Labadie, J.W.; Fontane, D.G. Indexed sequential hydrologic modeling for hydropower capacity estimation. J. Am. Water Resour. Assoc. 1997, 33, 1337–1349. [Google Scholar] [CrossRef]
- Adeloye, A.J.; Montaseri, M. Preliminary streamflow data analyses prior to water resources planning study/Analyses préliminaires des données de débit en vue d’une étude de planification des ressources en eau. Hydrol. Sci. J. 2002, 47, 679–692. [Google Scholar] [CrossRef] [Green Version]
- Toth, E. Estimation of flood warning runoff thresholds in ungauged basins with asymmetric error functions. Hydrol. Earth Syst. Sci. 2016, 20, 2383–2394. [Google Scholar] [CrossRef] [Green Version]
- Montanari, A.; Brath, A. A stochastic approach for assessing the uncertainty of rainfall-runoff simulations. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Kim, H.S.; Kang, D.S.; Kim, J.H. The BDS statistic and residual test. Stoch. Environ. Res. Risk Assess. 2003, 17, 104–115. [Google Scholar] [CrossRef]
- Vahdat, S.F.; Sarraf, A.; Shamsnia, A. Prediction of monthly mean Inflow to Dez Dam reservoir using time series models (Box-jenkins). In Proceedings of the 2011 International Conference on Environment and Industrial Innovation, Kuala Lumpur, Malaysia, 4–5 June 2011; Volume 12, pp. 162–166. [Google Scholar]
- Budu, K. Comparison of Wavelet-Based ANN and Regression Models for Reservoir Inflow Forecasting. J. Hydrol. Eng. 2014, 19, 1385–1400. [Google Scholar] [CrossRef]
- Zamani Sabzi, H.; King, J.P.; Abudu, S. Developing an intelligent expert system for streamflow prediction, integrated in a dynamic decision support system for managing multiple reservoirs: A case study. Expert Syst. Appl. 2017, 83, 145–163. [Google Scholar] [CrossRef]
- Szolgayová, E.P.; Danačová, M.; Komorniková, M.; Szolgay, J. Hybrid Forecasting of Daily River Discharges Considering Autoregressive Heteroscedasticity. Slovak J. Civ. Eng. 2017, 25, 39–48. [Google Scholar] [CrossRef] [Green Version]
- Harasami, F.; Akhgar, S.; Javan, M.; Shiri, J. Investigating the effect of previous time on modeling stage–discharge curve at hydrometric stations using GEP and NN models. ISH J. Hydraul. Eng. 2017, 23, 293–300. [Google Scholar] [CrossRef]
- Seo, Y.; Kim, S.; Kisi, O.; Singh, V.P.; Parasuraman, K. River Stage Forecasting Using Wavelet Packet Decomposition and Machine Learning Models. Water Resour. Manag. 2016, 30, 4011–4035. [Google Scholar] [CrossRef]
- Sanikhani, H.; Kisi, O.; Amirataee, B. Impact of climate change on runoff in Lake Urmia basin, Iran. Theor. Appl. Climatol. 2017. [Google Scholar] [CrossRef]
- Cadenas, E.; Rivar, W. Wind speed forecasting in three different regions of Mexico, using a hybrid ARIMAeANN model. Renew. Energy 2010, 35, 2732–2738. [Google Scholar] [CrossRef]
- Barak, S.; Sadegh, S.S. Forecasting energy consumption using ensemble ARIMA–ANFIS hybrid algorithm. Int. J. Electr. Power Energy Syst. 2016, 82, 92–104. [Google Scholar] [CrossRef] [Green Version]
- Zeng, D.; Xu, J.; Gu, J.; Liu, L.; Xu, G. Short Term Traffic Flow Prediction Using Hybrid ARIMA and ANN Models. In Proceedings of the 2008 Workshop on Power Electronics and Intelligent Transportation System, Guangzhou, China, 2–3 August 2008; pp. 621–625. [Google Scholar]
- Liu, H.; Tian, H.; Pan, D.; Li, Y. Forecasting models for wind speed using wavelet, wavelet packet, time series and Artificial Neural Networks. Appl. Energy 2013, 107, 191–208. [Google Scholar] [CrossRef]
- Khandelwal, I.; Adhikari, R.; Verma, G. Time Series Forecasting Using Hybrid ARIMA and ANN Models Based on DWT Decomposition. Procedia Comput. Sci. 2015, 48, 173–179. [Google Scholar] [CrossRef] [Green Version]
- Babu, C.N.; Reddy, B.E. A moving-average filter based hybrid ARIMA–ANN model for forecasting time series data. Appl. Soft Comput. 2014, 23, 27–38. [Google Scholar] [CrossRef]
- Fathian, F.; Fakheri Fard, A.; Ouarda, T.B.M.J.; Dinpashoh, Y.; Mousavi Nadoushani, S.S. Modeling streamflow time series using nonlinear SETAR-GARCH models. J. Hydrol. 2019, 573, 82–97. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Behmanesh, J.; Khalili, K. New Approaches for Estimation of Monthly Rainfall Based on GEP-ARCH and ANN-ARCH Hybrid Models. Water Resour. Manag. 2018, 32, 527–545. [Google Scholar] [CrossRef]
- Brown, R.L.; Durbin, J.; Evans, J.M. Techniques for Testing the Constancy of Regression Relationships over Time. J. R. Stat. Soc. Ser. B 1975, 37, 149–192. [Google Scholar] [CrossRef]
- Bollerslev, T.; Engle, R.F.; Nelson, D.B. Chapter 49 Arch models. Handb. Econom. 1994, 4, 2959–3038. [Google Scholar]
- Delleur, J.W.; Karamouz, M. Uncertainty in reservoir operation. In Optimal Allocation of Water Resources (Proceedings of the Fxeter Symposium); IAHS Publication: Washington, DC, USA, 1982. [Google Scholar]
- Kass, G.V. An Exploratory Technique for Investigating Large Quantities of Categorical Data. Appl. Stat. 2006, 29, 119. [Google Scholar] [CrossRef]
- Ma, J.; Tang, H.; Liu, X.; Hu, X.; Sun, M.; Song, Y. Establishment of a deformation forecasting model for a step-like landslide based on decision tree C5.0 and two-step cluster algorithms: A case study in the Three Gorges Reservoir area, China. Landslides 2017, 14, 1275–1281. [Google Scholar] [CrossRef]
- van Diepen, M.; Franses, P.H. Evaluating chi-squared automatic interaction detection. Inf. Syst. 2006, 31, 814–831. [Google Scholar] [CrossRef]
- Huang, G.-B.; Chen, L.; Siew, C.-K. Universial approximation using incremental constructive feedforward neural networks with random hidden nodes. Trans. Neural Netw. 2006, 17, 879–892. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Cui, N.; Zhao, L.; Hu, X.; Gong, D. Comparison of ELM, GANN, WNN and empirical models for estimating reference evapotranspiration in humid region of Southwest China. J. Hydrol. 2016, 536, 376–383. [Google Scholar] [CrossRef]
- Şahin, M. Comparison of modelling ANN and ELM to estimate solar radiation over Turkey using NOAA satellite data. Int. J. Remote Sens. 2013, 34, 7508–7533. [Google Scholar] [CrossRef]
- Miche, Y.; Sorjamaa, A.; Bas, P.; Simula, O.; Jutten, C.; Lendasse, A. OP-ELM: Optimally pruned extreme learning machine. IEEE Trans. Neural Netw. 2010, 21, 158–162. [Google Scholar] [CrossRef]
- Heddam, S.; Kisi, O. Extreme learning machines: A new approach for modeling dissolved oxygen (DO) concentration with and without water quality variables as predictors. Environ. Sci. Pollut. Res. 2017, 24, 16702–16724. [Google Scholar] [CrossRef]
- Attar, N.F.; Khalili, K.; Behmanesh, J.; Khanmohammadi, N. On the reliability of soft computing methods in the estimation of dew point temperature: The case of arid regions of Iran. Comput. Electron. Agric. 2018, 153, 334–346. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the Use of “Goodness of Fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 2005, 35, 233–241. [Google Scholar] [CrossRef]
- Wang, W.; Van Gelder, P.H.A.J.M.; Vrijling, J.K.; Ma, J. Testing and modelling autoregressive conditional heteroskedasticity of streamflow processes. Nonlinear Process. Geophys. 2005, 12, 55–66. [Google Scholar] [CrossRef] [Green Version]
- Rezaie-Balf, M.; Nowbandegani, S.F.; Samadi, S.Z.; Fallah, H.; Alaghmand, S. An ensemble decomposition-based artificial intelligence approach for daily streamflow prediction. Water (Switzerland) 2019, 11, 709. [Google Scholar] [CrossRef] [Green Version]
- Papathanasiou, C.; Makropoulos, C.; Mimikou, M. Hydrological modelling for flood forecasting: Calibrating the post-fire initial conditions. J. Hydrol. 2015, 529, 1838–1850. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.K.; Lu, W.Z.; Cao, S.Y.; Fang, D. Using Time-Delay Neural Network Combined with Genetic Algorithms to Predict Runoff Level of Linshan Watershed, Sichuan, China. J. Hydrol. Eng. 2007, 12, 231–236. [Google Scholar] [CrossRef]
- Makkeasorn, A.; Chang, N.B.; Zhou, X. Short-term streamflow forecasting with global climate change implications—A comparative study between genetic programming and neural network models. J. Hydrol. 2008, 352, 336–354. [Google Scholar] [CrossRef]
- Nourani, V.; Hosseini Baghanam, A.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet-Artificial Intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]







| Streams | Stations | Geographic Properties | ||
|---|---|---|---|---|
| Longitude | Latitude | Elevation (m) | ||
| Nazluchai | Tapik | 00-44-54 | 00-37-40 | 1410 |
| Baranduzchai | Dizaj | 00-45-04 | 00-37-23 | 1320 |
| Rivers | Stations | Xmin | Xmax | Xmean (m3/s) | Sx | Csx |
|---|---|---|---|---|---|---|
| Nazluchai | Tapik | 0.017 | 104.378 | 11.101 | 15.502 | 2.822 |
| Baranduzchai | Dizaj | 0.031 | 46.125 | 7.269 | 7.996 | 2.055 |
| Stream (Station) | Skewness before Normalization | Normalization | Skewness after Normalization |
|---|---|---|---|
| Baranduzchai (Dizaj) | 2.05542 | −0.000187245 | |
| Nazluchai (Tapik) | 2.821872 | 0.000861473 |
| Station | Model | Statistical Error Indices | ||||
|---|---|---|---|---|---|---|
| R | RMSE (m3/s) | NSE | MAE (m3/s) | RSD | ||
| Total available data in calibration stage | ||||||
| Dizaj | Dizaj-OPELM | 0.92 | 3.378 | 0.84 | 1.854 | 0.387 |
| Dizaj-CHAID | 0.91 | 3.655 | 0.82 | 2.144 | 0.419 | |
| Tapik | Tapik-OPELM | 0.91 | 7.428 | 0.81 | 3.374 | 0.429 |
| Tapik-CHAID | 0.90 | 7.816 | 0.79 | 3.697 | 0.451 | |
| Total available data in validation stage | ||||||
| Dizaj | Dizaj-OPELM | 0.89 | 2.568 | 0.78 | 1.544 | 0.463 |
| Dizaj-CHAID | 0.94 | 1.571 | 0.91 | 0.863 | 0.328 | |
| Tapik | Tapik-OPELM | 0.86 | 5.185 | 0.67 | 2.663 | 0.566 |
| Tapik-CHAID | 0.89 | 4.329 | 0.77 | 2.253 | 0.473 | |
| Stream (Station) | Distribution | Log-Likelihood | ARCH Model |
|---|---|---|---|
| Baranduzchai (Dizaj) | Gaussian | −361.7161 | |
| Nazluchai (Tapik) | Gaussian | −375.2455 |
| Station | Model | Statistical Error Indices | ||||
|---|---|---|---|---|---|---|
| R | RMSE (m3/s) | NSE | MAE (m3/s) | RSD | ||
| Total available data in calibration stage | ||||||
| Dizaj | Dizaj-ARCH-OPELM | 0.94 | 2.168 | 0.81 | 1.268 | 0.319 |
| Dizaj-ARCH-CHAID | 0.92 | 2.395 | 0.83 | 2.039 | 0.348 | |
| Tapik | Tapik-ARCH-OPELM | 0.92 | 6.896 | 0.82 | 3.215 | 0.422 |
| Tapik-ARCH-CHAID | 0.93 | 5.678 | 0.85 | 3.167 | 0.418 | |
| Total available data in validation stage | ||||||
| Dizaj | Dizaj-ARCH-OPELM | 0.91 | 1.496 | 0.38 | 3.903 | 0.426 |
| Dizaj-ARCH-CHAID | 0.96 | 1.289 | 0.92 | 0.719 | 0.301 | |
| Tapik | Tapik-ARCH-OPELM | 0.89 | 3.671 | 0.78 | 2.018 | 0.487 |
| Tapik-ARCH-CHAID | 0.94 | 2.662 | 0.86 | 1.467 | 0.419 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Attar, N.F.; Pham, Q.B.; Nowbandegani, S.F.; Rezaie-Balf, M.; Fai, C.M.; Ahmed, A.N.; Pipelzadeh, S.; Dung, T.D.; Nhi, P.T.T.; Khoi, D.N.; et al. Enhancing the Prediction Accuracy of Data-Driven Models for Monthly Streamflow in Urmia Lake Basin Based upon the Autoregressive Conditionally Heteroskedastic Time-Series Model. Appl. Sci. 2020, 10, 571. https://doi.org/10.3390/app10020571
Attar NF, Pham QB, Nowbandegani SF, Rezaie-Balf M, Fai CM, Ahmed AN, Pipelzadeh S, Dung TD, Nhi PTT, Khoi DN, et al. Enhancing the Prediction Accuracy of Data-Driven Models for Monthly Streamflow in Urmia Lake Basin Based upon the Autoregressive Conditionally Heteroskedastic Time-Series Model. Applied Sciences. 2020; 10(2):571. https://doi.org/10.3390/app10020571
Chicago/Turabian StyleAttar, Nasrin Fathollahzadeh, Quoc Bao Pham, Sajad Fani Nowbandegani, Mohammad Rezaie-Balf, Chow Ming Fai, Ali Najah Ahmed, Saeed Pipelzadeh, Tran Duc Dung, Pham Thi Thao Nhi, Dao Nguyen Khoi, and et al. 2020. "Enhancing the Prediction Accuracy of Data-Driven Models for Monthly Streamflow in Urmia Lake Basin Based upon the Autoregressive Conditionally Heteroskedastic Time-Series Model" Applied Sciences 10, no. 2: 571. https://doi.org/10.3390/app10020571
APA StyleAttar, N. F., Pham, Q. B., Nowbandegani, S. F., Rezaie-Balf, M., Fai, C. M., Ahmed, A. N., Pipelzadeh, S., Dung, T. D., Nhi, P. T. T., Khoi, D. N., & El-Shafie, A. (2020). Enhancing the Prediction Accuracy of Data-Driven Models for Monthly Streamflow in Urmia Lake Basin Based upon the Autoregressive Conditionally Heteroskedastic Time-Series Model. Applied Sciences, 10(2), 571. https://doi.org/10.3390/app10020571