High-Velocity Impact Performance of Aluminum and B₄C/UHMW-PE Composite Plate for Multi-Wall Shielding

Abstract

Three types of multi-wall shielding were experimentally investigated for their performances under the high-velocity impact of a cm-size cylindrical projectile by using a two-stage light-gas gun. The three shields contained the same two aluminum bumpers but different rear walls, which were 7075-T651 aluminum (Al) plate, boron carbide (B₄C)/Al 7075-T651/Kevlar composite plate and B₄C/ultra-high molecular weight polyethylene (UHMW-PE) composite plate. The impact test was carried out using a cylindrical shape of 6 g mass 7075-T651 Al projectile in a speed range (1.6 to 1.9 km/s) to achieve an effective shield configuration. A numerical simulation was undertaken by using ANSYS Autodyn-3D and the results of this were in good agreement with the experimental results. Meanwhile, both the experimental and the numerical simulation results indicated that B₄C/UHMW-PE composite plates performed a better interception of the high-velocity projectiles within the specific speed range and could be considered as a good configuration for intercepting large fragments in shielding design.

1. Introduction

Since Fred L. Whipple [1] proposed the Whipple shield in 1947, many scholars have continued to study and optimize the shield, including Whipple, Nextel/Kevlar Stuffed Whipple and multi-wall shields in general [2]. Normally, the shield design with a lower surface density is better when the protection requirements are met. To achieve this, some innovative materials, such as ceramic materials, polymer materials, and composites, have been developed and ballistic experiments of these shielding materials have been carried out for potential applications [3,4,5]. A “small debris” with a size of 1–10 cm cannot be monitored and tracked due to detection technology limitations. In addition, because of its large size and high kinetic energy, “small debris” poses the greatest threat to spacecraft [6]. However, the existing research on space debris protection is mostly focused on micro-sized space debris with a diameter of less than 1 cm. There are few studies on the impact and protection effects of cm-size fragments. As a practical matter, most of the protective shields have been investigated from ballistic impact databases involving only spherical projectiles. However, debris can take any shape. Furthermore, it has been demonstrated that non-spherical projectiles can be more destructive than equal mass spherical projectiles under the same impact conditions [7,8]. Therefore, ballistic impact tests of non-spherical projectiles are valuable and necessary for the study of debris protection.

Compared with conventional ceramic materials, boron carbide (B₄C) exhibits not only higher hardness and lower density properties, but also possesses a better chemical stability at high temperatures, which has been used in civil, aerospace and military applications [9]. Ultra-high molecular weight polyethylene (UHMW-PE) has a good impact resistance and a great energy absorption performance [10]. Some scholars [11,12] have applied UHMW-PE to the design of Whipple protection structures and conducted extensive research. In this paper, the multi-wall shield of high-velocity cm-size debris was designed and studied. The cylindrical Al 7075-T651 projectile was launched by a two-stage light-gas gun and impacted the multi-wall shield in the velocity range of 1.6–1.9 km/s. Three effective shield configurations were obtained through experiments. The best performing shield configuration with the B₄C/UHMW-PE composite plate rear wall, as well as the comparison configuration with the aluminum rear wall, was further analyzed by a numerical simulation. Meanwhile, the mechanism of the multi-wall shield against the projectile was investigated.

2. Experimental Procedure

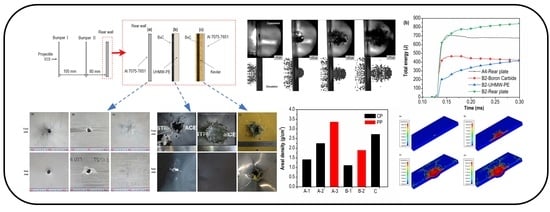
2.1. The Design of Shield Configurations

The sketch of shield configurations is shown in Figure 1. The three configurations contained the same two bumpers but different rear walls, which were Al 7075-T651 plate in Configuration A (Con. A), B₄C/UHMW-PE composite plate in Configuration B (Con. B) and Kevlar /B₄C/ Kevlar/Al 7075-T651 composite plate in Configuration C (Con. C). The two bumpers were 3 mm-thick Al 7075-T651 plates with a spacing of 100 mm, and the spacing between bumper II and the rear wall was 80 mm. Detailed parameters of the rear wall are provided in

Table 1. The shield configurations.

Configuration No.	Composition of the Rear Plate	Areal Density (g/cm2)
A-1	5 mm Al7075-T651	1.402
A-2	8 mm Al7075-T651	2.243
A-3	12 mm Al7075-T651	3.365
B-1	2 mm B4C/6 mm UHMW-PE	1.091
B-2	4 mm B4C/8 mm UHMW-PE	1.790
C	2 mm Kevlar/6 mm B4C/2 mm Kevlar/2 mm Al7075-T651	2.730

. The size of all of the bumpers was 200 × 200 × 3 mm. The B₄C/UHMW-PE composite plate, as well as the composite plate in Configuration C, was clamped in a square frame, as represented in Figure 2. The density of the Al 7075-T651, B₄C, UHMW-PE and Kevlar plates were 2.804, 2.516, 0.98 and 1.65 g/cm³, respectively. The woven pattern for UHMWPE was a cross-ply layup with an angle of 90°. The matrix of the Kevlar was orthogonal-braided and the fiber percentage was about 70%. It is worth mentioning that the woven pattern and molding process of UHMW-PE affects the mechanical properties of the material. The molding process technology of UHMW-PE is mature and the performance of different samples varies by a small amount, which affects the ballistic result slightly. The projectiles used were Al 7075-T651 cylinder—17.2 mm long by 12.6 mm in diameter.

2.2. Measurement Method and Test Equipment

The protective ability of the shield was evaluated by whether the rear wall was perforated. The results were presented as a complete penetration (CP) or a partial penetration (PP) [13]. The tests were conducted on the 14.5 mm caliber two-stage light-gas gun at the Beijing Institute of Technology (BIT), as shown in Figure 3. The velocity of the projectile was measured with a magnetic velocimeter, ranging from 1.6 to 1.9 km/s. The shield was set up in the target chamber with an environmental pressure of approximately 30 Pa. A high-speed camera system was used to record the impact process. The diagrammatic sketch of the experimental apparatus is shown in Figure 4.

3. Numerical Modeling

The numerical simulations were performed using the Autodyn-3D finite element program, which has a good function for simulating high-strain-rate phenomena, such as impact and explosion [14]. The 3D modeling was performed using smooth particle–fluid dynamics (SPH) coding and Lagrange coding. SPH is a meshless modeling technology, and the debris cloud phenomenon generated by high-speed impact can be effectively simulated by using SPH coding. Lagrange coding is suitable for large deformations caused by tension or shear loadings and internal material fracture problems [15]. The relatively low-strain-rate deformation parts (rear plate) of the model were solved by the Lagrange coding, and the high-strain-rate deformation parts (projectile and bumpers) were solved by the SPH coding, which made the simulation accurate and efficient.

In this study, the Johnson-Cook material model (JC model) was used for the Al 7075-T651 projectile and shields. In this model, the stress equation is expressed as

$$\sigma =(A+B{\epsilon }_p^n)\left(1+C\ln ({\dot{\epsilon }}_p/{\dot{\epsilon }}_{p0})\right)\left(1-{\left(\frac{T-T_0}{T_m-T_0}\right)}^m\right)$$

(1)

where ${\epsilon }_p$ and ${\dot{\epsilon }}_p$ is the plastic strain and plastic strain rate, respectively. $A,B,C,m,n,{\dot{\epsilon }}_{p0},T_0$ and $T_m$ are the constants determined by the experiment and $T$ is the absolute temperature. A detailed description of the JC model can be found in Ref. [16]. The JC model parameters are given in

Table 2. The material parameters for Al 7075-T651 [17].

Parameter	Symbol	Values
Density (g/cm3)	ρ0z	2.804
Shear modulus (GPa)	G	29
Static yield strength (GPa)	A	527
Strain-hardening coefficient (GPa)	B	575
Strain-hardening exponent	n	0.72
Strain rate coefficient	C	0.017
Reference strain rate (s−1)	${\dot{\epsilon }}_0$	1.0
Thermal softening exponent	m	1.61
Reference temperature (K)	t0	298
Melting temperature	tm	900
Damage constant	D1	0.11
Damage constant	D2	0.572
Damage constant	D3	−3.446
Damage constant	D4	0.016
Damage constant	D5	1.099

[17].

The Johnson–Holmquist material model (JH-2 model) was used for modeling the B₄C layer of Configuration II. The actual equivalent stress is given as

$$\sigma =(1-D){\sigma }_i(p,\dot{\epsilon })+D{\sigma }_f(p,\dot{\epsilon })$$

(2)

where $D\in [0,1]$ is the damage parameter. ${\sigma }_i$ and ${\sigma }_f$ are the actual equivalent intact stress and the fractured stress, which are the functions of pressure $p$ and strain rate $\dot{\epsilon }$.

$${\sigma }_i(p,\dot{\epsilon })=A{\sigma }_{HEL}{\left(\frac{{\sigma }_{hyd}+p}{p_{HEL}}\right)}^N\left(1+C\ln (\dot{\epsilon }/{\dot{\epsilon }}_0)\right)$$

(3)

$${\sigma }_f(p,\dot{\epsilon })=B{\sigma }_{HEL}{\left(p/p_{HEL}\right)}^M\left(1+C\ln \left(\dot{\epsilon }/{\dot{\epsilon }}_0\right)\right)\le S_{f\max }{\sigma }_{HEL}$$

(4)

where $A,N,C,B,M,S_{f\max }$ are the dimensionless parameters, ${\sigma }_{hyd}$ is the maximum tensile hydrostatic stress, ${\dot{\epsilon }}_0$ is strain rate, ${\sigma }_{HEL}$ and $p_{HEL}$ are the equivalent stress and pressure at the Hugoniot elastic limit (HEL). A detailed description of the JH-2 model can be found in Reference [18] and the model parameters are given in

Table 3. The parameters for boron carbide used in Johnson–Holmquist’s model [19].

Parameter	Symbol	Values
Density (g/cm3)	ρ0z	2.508
Bulk modulus (GPa)	K1	233
Pressure coefficient (GPa)	K2	−593
Pressure coefficient (GPa)	K3	2800
Shear modulus (GPa)	G	197
Hugoniot elastic limit (HEL) (GPa)	HEL	19.0
Intact strength coefficient	A	0.9637
Intact strength exponent	N	0.67
Strain rate coefficient	C	0.005
Fracture strength coefficient	B	0.7311
Fracture strength exponent	M	0.85
Maximum fracture strength	Sfmax	0.2045
Damage coefficient	D1	0.001
Damage exponent	D2	0.5
Bulking factor	β	1.0
Tensile strength (GPa)	σhyd	0.26

[19].

The non-linear orthotropic material model (Ortho model) developed in [20,21,22,23] is used for modeling the UHMW-PE composite. The material model includes orthotropic coupling of the material volumetric and deviatoric response proposed by Anderson et al. [24], the non-linear equation of state and orthotropic hardening proposed by Chen et al. [25], the stress-based composite failure criteria, and the orthotropic energy-based softening [26]. For the equation of state, the pressure is defined by

$$p=p({\epsilon }_{vol},e)-1/3(C_{11}+C_{21}+C_{31}){\epsilon }_{11}^d-1/3(C_{12}+C_{22}+C_{32}){\epsilon }_{22}^d-1/3(C_{13}+C_{23}+C_{33}){\epsilon }_{33}^d$$

(5)

where $C$ are coefficients of the stiffness matrix and ${\epsilon }_{11,22,33}^d$ are the deviatoric strains in the principal directions. The pressure contribution from the volumetric strain is expressed as

$$p({\epsilon }_{vol},e)=p_r(v)+\mathsf{\Gamma }(v)/v\left[e-e_r(v)\right]$$

(6)

where $v$ is the volume, $e$ is the internal energy and $\mathsf{\Gamma }(v)$ is the Grüneisen coefficient. $p_r(v)$ and $e_r(v)$ are the reference pressure and the internal energy.

The quadratic yield surface proposed by Chen et al. [25] is used as the strength model.

$$\begin{array}{cc}\hfill f({\sigma }_{ij})& =a_{11}{\sigma }_{11}^2+a_{22}{\sigma }_{22}^2+a_{33}{\sigma }_{33}^2+2a_{12}{\sigma }_{11}{\sigma }_{22}+2a_{23}{\sigma }_{22}{\sigma }_{33}+2a_{13}{\sigma }_{11}{\sigma }_{33}\hfill \\ & +2a_{44}{\sigma }_{23}^2+2a_{55}{\sigma }_{31}^2+2a_{66}{\sigma }_{12}^2=k\hfill \end{array}$$

(7)

where $a_{ij}$ are the plasticity coefficients of the material, ${\sigma }_{ij}$ are stresses in the principal directions and $k$ is a state variable.

The failure model is based on a combined stress criterion and is initiated when

$${\left(\frac{{\sigma }_{ii}}{S_{ii}(1-D_{ii})}\right)}^2+{\left(\frac{{\sigma }_{ij}}{S_{ij}(1-D_{ij})}\right)}^2+{\left(\frac{{\sigma }_{ki}}{S_{ki}(1-D_{ki})}\right)}^2\ge 1;i,j,k=1,2,3$$

(8)

where $S_{ii}$ is the failure strength. The damage parameter $D_{ii}$ is defined by

$$D_{ii}=\frac{L{\sigma }_{ii,f}{\epsilon }_{cr}}{2G_{ii,f}}$$

(9)

where $L$ is the characteristic cell length, ${\epsilon }_{cr}$ is the crack strain and $G_{ii,f}$ is the fracture energy.

All of the UHMW-PE composite material parameters are given in

Table 4. The parameters for UHMW-PE used in non-linear orthotropic material model [26].

Parameter	Symbol	Values
EOS: Orthotropic
Density (g/cm3)	ρ	0.98
Young’s modulus 11 (GPa)	E11	3.62
Young’s modulus 22 (GPa)	E22	51.1
Young’s modulus 33 (GPa)	E33	51.1
Poisson’s ratio 12	v12	0.013
Poisson’s ratio 23	v23	0
Poisson’s ratio 31	v31	0.5
Shear modulus 12 (GPa)	G12	2.0
Shear modulus 23 (GPa)	G23	0.192
Shear modulus 31 (GPa)	G31	2.0
Volumetric response: Shock
Grüneisen coefficient	Γ	1.64
Parameter C1 (m/s)	c0	3570
Parameter S1	S	1.3
Reference temperature (K)	T0	293
Specific heat (J/kg·K)	cv	1850
Failure: Orthotropic softening
Tensile failure stress 11 (GPa)	S11	1.01 × 1020
Tensile failure stress 22 (GPa)	S22	1.15
Tensile failure stress 33 (GPa)	S33	1.15
Maximum shear stress 12 (GPa)	S12	0.575
Maximum shear stress 23 (GPa)	S23	0.12
Maximum shear stress 31 (GPa)	S31	0.575
Fracture energy 11 (J/m2)	G11C	790
Fracture energy 22 (J/m2)	G22C	30
Fracture energy 33 (J/m2)	G33C	30
Fracture energy 12 (J/m2)	G12C	1460
Fracture energy 23 (J/m2)	G23C	1460
Fracture energy 31 (J/m2)	G31C	1460
Damage coupling coefficient	C	0
Strength: Orthotropic yield
Plasticity constant 11	A11	0.016
Plasticity constant 22	A22	6 × 10−4
Plasticity constant 33	A33	6 × 10−4
Plasticity constant 12	A12	0
Plasticity constant 13	A13	0
Plasticity constant 23	A23	0
Plasticity constant 44	A44	1
Plasticity constant 55	A55	1.7
Plasticity constant 66	A66	1.7
Eff. stress #1 (GPa)	σeff#1	1.48 × 10−3
Eff. stress #2 (GPa)	σeff#2	7.0 × 10−3
Eff. stress #3 (GPa)	σeff#3	0.027
Eff. stress #4 (GPa)	σeff#4	0.04
Eff. stress #5 (GPa)	σeff#5	0.05
Eff. stress #6 (GPa)	σeff#6	0.06
Eff. stress #7 (GPa)	σeff#7	0.08
Eff. stress #8 (GPa)	σeff#8	0.098
Eff. stress #9 (GPa)	σeff#9	0.2
Eff. stress #10 (GPa)	σeff#10	1
Eff. plastic strain #1	εeff#1	0
Eff. plastic strain #2	εeff#2	0.01
Eff. plastic strain #3	εeff#3	0.1
Eff. plastic strain #4	εeff#4	0.15
Eff. plastic strain #5	εeff#5	0.175
Eff. plastic strain #6	εeff#6	0.19
Eff. plastic strain #7	εeff#7	0.2
Eff. plastic strain #8	εeff#8	0.205
Eff. plastic strain #9	εeff#9	0.21
Eff. plastic strain #10	εeff#10	0.215

. [26]

In the simulation analysis, the quarter model was applied to reduce calculation time. The projectile and the Al 7075-T651 bumpers were modeled using SPH coding with a smooth length of 0.5 mm. The rear wall was meshed by a Lagrange grid with all the configurations and a hierarchical partition of thirty 0.5 mm fixed-size cells were assigned to fifty cells in each in-plane direction. A gap of 0.01 mm was set between the layers of the rear wall, according to the experimental situation.

4. Results and Discussion

4.1. Experiment Results

The role of the first two bumpers was to break the projectile and reduce its kinetic energy. The typical damage of the first two layers is shown in Figure 5. It can be obtained that Bumper I exhibited only one perforated hole with a diameter of about 18.6 mm, which proved that the projectile’s posture was good. On the other hand, Bumper II exhibited multiple small perforated holes and craters around a big, irregularly-shaped perforated hole. The projectile carried a large initial kinetic energy due to its large mass and high velocity. After the projectile perforated Bumper I, a debris cloud was formed which then impacted Bumper II. Partially broken projectile and debris clouds still penetrated Bumper II and caused perforation or other forms of damage to the rear wall.

The results of the impact tests are listed in

Table 5. The results of the impact tests.

Configuration No.	Velocity (km/s)	Results
A-1	1.70	CP
A-2	1.64	CP
A-3	1.62	PP
B-1	1.61	CP
B-2	1.86	PP
C	1.61	CP

. The typical experimental results of damage of the rear wall in each configuration are presented in Figure 6 and Figure 7. According to the damage of the rear wall, it is evident that the rear walls of Configurations A-1, A-2, B-1 and C were penetrated (i.e., CP) while the rear walls of Configurations A-3 and B-2 were not penetrated (i.e., PP). The rear wall of Configuration A-1 (i.e., 5 mm-thick Al 7075) was perforated with a diameter of 20 mm, and there were two obvious impact craters near the perforated area. The rear wall of Configuration A-2 (i.e., 8 mm-thick Al 7075) was penetrated and the back was scabbing. The Configuration A-3 rear wall (i.e., 12 mm-thick Al 7075) was not perforated, and there were some craters on the front side, with no bumps on the back. From Figure 7, it can be seen that the B₄C board was fractured in all of the configurations. In Configuration B-1, the projectile perforated the UHMW-PE layer and caused the fiberboard to bulge by approximately 83 mm. However, in Configuration B-2, the UHMW-PE layer was not perforated due to the increased thickness of B₄C and UHMW-PE. The UHMW-PE board posed several long cracks and bulged by 9 mm. In Configuration C, the rear wall was completely perforated. The outermost Al 7075-T651 layer posed six approximately symmetric long cracks, starting from the perforated hole.

The areal density of the rear walls and the experimental results are shown in Figure 8. It can be seen that the B₄C/UHMW-PE composite plate (configuration B) prevented the penetration of the projectile most effectively. The energy of the projectile was dissipated through the breaking of the B₄C and the large deformation of the UHMW-PE. This configuration design could greatly reduce the mass of the protection system, while still meeting the protection requirements. It is worth mentioning that the B₄C and Kevlar fiber plates were used in Configuration C—the design idea of this was to make the Kevlar cover the B₄C to reduce the debris flying out. However, its protective effect was not satisfactory. A possible reason for this is that, although Kevlar exhibits excellent tensile properties, it could not provide support for the B₄C like the UHMW-PE, and boron carbide had poor shear resistance, so the role of the B₄C was not exerted. Kevlar usually absorbs energy through large deformations. In Configuration C, the front layer of Kevlar contributed less to the overall protection of the rear plate, while the last layer of aluminum obstructed the deformation of the second layer of Kevlar.

4.2. Numerical Modeling Analysis

It has been experimentally proved that Configuration B with the B₄C/UHMW-PE composite plate as the rear wall was the best shield configuration among the three. Numerical simulations were used to analyze the above experimental results in more detail. The experimental conditions of Configuration A were also numerically calculated for comparison. The variation in the projectile residual velocity for the five conditions under the two shield configurations is shown in Figure 9. It is worth noting that the termination time (0.4 ms) was long enough for the projectile to reach a complete stop and short enough to prevent a redundant computation time. The numerical results were consistent with the experimental results. The debris cloud formed after the projectile penetrated the first two bumpers, which was almost identical to the debris cloud image captured in the experiment, as shown in Figure 10. The image scale was calibrated before the test, so we got the velocity of the debris head with 1.01 km/s. The velocity of the debris head obtained from the simulation was 0.95 km/s, which showed good agreement with the experimental results. Figure 11 and Figure 12 show the damage contours of the bumpers and the rear plates, both in the experiments and the simulations. The comparison in damage size and the pattern between the simulation and the experimental results exhibited a good agreement. Through the above results, the reliability of the numerical calculation model was verified.

To further compare and analyze the impact process of Configuration A and Configuration B, we carried out a numerical simulation of the Al 7075-T651 plate as the rear wall at an impact velocity of 1.86 km/s, in which the areal density of the rear wall was the same as that of Configuration B-2. The numerical calculation was noted as A-4. The variation in the projectile residual velocity with time for Configurations A-4 and B-2 is shown in Figure 13. For the first ~0.13 ms, the projectile perforated two bumpers and slowed down to ~1050 m/s. In the first ~0.01 ms of the remaining projectile impacting the rear wall, the projectile slowed down to ~440 m/s and the deceleration behavior was almost the same for the two configurations but, following this, time deviations occurred, as seen in Figure 13. The projectile velocity in Configuration B-2 decreased more slowly and eventually dropped to zero, while the rear wall of Configuration A-4 was perforated and the projectile residual velocity was ~219 m/s. In accordance with this, the B₄C/UHMW-PE composite plate intercepted the projectile more effectively than the single Al 7075-T651 plate.

The energy absorption of the rear plate during the process of the remaining projectile and debris impact, as well as the energy transfer information during the impact process, were obtained from the simulation. Figure 14a,b shows the kinetic energy and total energy histories of the Al 7075-T651 rear wall for Configuration A-4 and the B₄C/UHMW-PE composite plate for Configuration B-2. As the projectile penetration progressed, the kinetic energy of the rear plate increased initially and then gradually decreased, as seen in Figure 14a. At ~0.14 ms, the kinetic energy of the rear plate of both configurations reached the maximum value. At this moment, the Al 7075-T651 plate in Configuration A-4 was perforated and the B₄C layer in Configuration B-2 was broken. It can be seen from Figure 14a that the B₄C layer with Configuration B-2 had the lowest kinetic energy due to the constraint of the UHMW-PE layer. The total energy of the rear plate characterized the energy absorption of the projectile. The total energy of the B₄C/UHMW-PE composite plate in Configuration B-2 was higher than that of the Al 7075-T651 plate in Configuration A-4, which proved that the composite plate exhibited better protection performance. In our view, the B₄C layer preliminarily resisted the projectile and broke up to absorb most of the energy. Then, the UHMW-PE layer effectively buffered and stopped the remaining projectile and debris due to its high tensile strength and large bulge. Figure 15 and Figure 16 show the produced damage in the rear wall of the two configurations during the ballistic impact process. As shown in Figure 15, several craters were formed on the front side of the Al 7075-T651 rear plate of Configuration A-4 after the projectile impact, and then, at 0.01 ms, tensile failure occurred on the backside of the rear plate. As the penetration process continued, the tensile failure zone became larger and the Al 7075-T651 rear plate was perforated eventually. It could be seen from Figure 16 that the B₄C/UHMW-PE composite plate of Configuration B-2 exhibited different failure modes. The B₄C layer near the projectile impact point broke initially and was accompanied by the rapid propagation of the crack. Then, the brittle fracture area was gradually enlarged and the long cracks were also increased. Meanwhile, the UHMW-PE layer supported the B₄C layer and exhibited a large bulge. The main damage area of the rear plate was concentrated near the projectile impact point in both configurations. The damage area of the Al 7075-T651 plate in Configuration A-4 was more concentrated, and the B₄C layer damage area was larger, accompanied by multiple crack propagation, which was consistent with the experimental phenomenon.

5. Conclusions

In summary, we designed and proposed three kinds of shield configurations for high-velocity (1.6–1.9 km/s) impact of cm-size Al 7075-T651 projectiles, and the ballistic performance was investigated both experimentally and numerically. Compared with aluminum rear wall configuration, the B₄C/UHMW-PE composite plate exhibited superior protection performance. The B₄C layer absorbed energy by brittle fracture, and the UHMW-PE layer effectively buffered and stopped the remaining projectile due to its high tensile stress and large bulge. The numerical calculation model was effectively validated by experiments, which provided a basis for further research. However, to obtain a more reliable shield for cm-size debris, ballistic experiments with higher projectile impact velocities necessary in future works.