Flaw Detection on a Tilted Particleboard by Use of the Spec-Radiation Method
Abstract
:1. Introduction
2. Materials and Methods
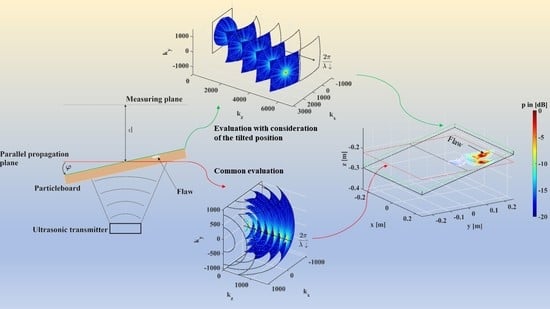
2.1. The Spec-Radiation Method
2.2. The Spec-Radiation Method for Tilted Particleboards
2.3. Practical Implementation
2.4. Experimental Setup
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ToF | Time of flight |
| FFT | Fast Fourier transformation |
| iFFT | Inverse fast Fourier transformation |
References
- Sokolov, S.Y. On the problem of the propagation of ultrasonic oscillations in various bodies. Elek. Nachr. Tech. 1929, 6, 454–460. [Google Scholar]
- Deutsch, V.; Platte, M.; Vogt, M. Ultraschallprüfungen; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar] [CrossRef]
- Krautkrämer, J.; Krautkrämer, H. Werkstoffprüfung mit Ultraschall; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar] [CrossRef]
- Lerch, R.; Sessler, G.M.; Wolf, D. Technische Akustik; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Dahmen, S.; Ketata, H.; Ghozlen, M.H.B.; Hosten, B. Elastic constants measurement of anisotropic Olivier wood plates using air-coupled transducers generated Lamb wave and ultrasonic bulk wave. Ultrasonics 2010, 50, 502–507. [Google Scholar] [CrossRef] [PubMed]
- Chimenti, D.E. Review of air-coupled ultrasonic materials characterization. Ultrasonics 2014, 54, 1804–1816. [Google Scholar] [CrossRef] [PubMed]
- Solodov, I.; Dillenz, A.; Kreutzbruck, M. A new mode of acoustic NDT via resonant air-coupled emission. J. Appl. Phys. 2014, 121, 245101. [Google Scholar] [CrossRef]
- Marhenke, T.; Neuenschwander, J.; Furrer, R.; Zolliker, P.; Twiefel, J.; Hasener, J.; Wallaschek, J.; Sanabria, S. Air-coupled ultrasound time reversal (ACU-TR) for subwavelength non-destructive imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 651–663. [Google Scholar] [CrossRef]
- Sanabria Martín, S.J. Air-Coupled Ultrasound Propagation and Novel Non-Destructive Bonding Quality Assessment of Timber Composites; ETH: Zurich, Switzerland, 2012. [Google Scholar] [CrossRef]
- Gyekenyesi, A.L.; Harmon, L.M.; Kautz, H.E. The Effect of Experimental Conditions on Acousto-Ultrasonic Reproducibility. Proc. SPIE 2002, 4704, 177–186. [Google Scholar] [CrossRef]
- Schafer, M. The Effect of Experimental Conditions on Acousto-Ultrasonic Reproducibility. IEEE Ultrason. Symp. 2000, 771–778. [Google Scholar] [CrossRef]
- Jasiuniene, E.; Raisutis, R.; Sliteris, R.; Voleiis, A.; Jakas, M. Ultrasonic NDT of wind turbine blades using contact pulse-echo immersion testing with moving water container. Ultragarsas J. 2008, 63, 28–32. [Google Scholar]
- Fang, Y.; Lin, L.; Feng, H.; Lu, Z.; Emms, G.W. Review of the use of air-coupled ultrasonic technologies for nondestructive testing of wood and wood products. Comput. Electron. Agric. 2017, 137, 79–87. [Google Scholar] [CrossRef]
- Sanabria, S.; Mueller, C.; Neuenschwander, J.; Niemz, P.; Sennhauser, U. Air-coupled ultrasound as an accurate and reproducible method for bonding assessment of glued timber. Wood Sci. Technol. 2011, 45, 645–659. [Google Scholar] [CrossRef] [Green Version]
- Hillger, W.; Bühling, L.; Ilse, D. Review of 30 years ultrasonic systems and developments for the future. In Proceedings of the ECNDT2014, Prague, Czech Republic, 6–10 October 2014. [Google Scholar]
- Álvarez Arenas, T.E.G. Acoustic Impedance Matching of Piezoelectric Transducers to the Air. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 51, 624–633. [Google Scholar] [CrossRef]
- Dunky, D.; Niemz, P. Holzwerkstoffe und Leime; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Niemz, P. Bestimmung von Fehlverklebungen mittels Schallaufzeitmessung. Holz Roh Werkst. 1995, 53, 236. [Google Scholar] [CrossRef]
- Bucur, V.; Böhnke, I. Factors affecting ultrasonic measurements in solid wood. Ultrasonics 1994, 32, 385–390. [Google Scholar] [CrossRef]
- Raichel, D.R. The Science and Applications of Acoustic; Springer Science+Business Media: New York, NY, USA, 2006. [Google Scholar]
- Döring, D. Air-Coupled Ultrasound and Guided Acoustic Waves for Application in Non-Destructive Material Testing; OPUS: Stuttgart, Germany, 2011. [Google Scholar] [CrossRef]
- Laybed, Y.; Huang, L. Ultrasound time-reversal MUSIC imaging with diffraction and attenuation compensation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2186–2200. [Google Scholar] [CrossRef]
- Gabor, D. Holography. Science 1972, 177, 299–313. [Google Scholar] [CrossRef]
- Marhenke, T.; Sanabria, S.; Chintada, B.; Furrer, R.; Neuenschwander, J.; Goksel, O. Acoustic field characterization of medical array transducers based on unfocused transmits and single-plane hydrophone measurements. Sensors 2019, 19, 863. [Google Scholar] [CrossRef] [Green Version]
- Marhenke, T.; Sanabria, S.; Twiefel, J.; Furrer, R.; Neuenschwander, J.; Wallaschek, J. Three dimensional sound field computation and optimization of the delamination detection based on the re-radiation. In Proceedings of the 12th ECNDT, Gothenburg, Sweden, 11–15 June 2018. [Google Scholar]
- Sanabria, S.; Marhenke, T.; Furrer, R.; Neuenschwander, J. Calculation of volumetric sound field of pulsed air-coupled ultrasound transducers based on single-plane measurements. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 72–84. [Google Scholar] [CrossRef]
- Schmelt, A.; Marhenke, T.; Twiefel, J. Identifying objects in a 2D-space utilizing a novel combination of a re-radiation based method and of a difference-image-method. In Proceedings of the ICA 2019, Aachen, Germany, 9–13 September 2019. [Google Scholar]
- Schmelt, A.; Marhenke, T.; Hasener, J.; Twiefel, J. Investigation and Enhancement of the Detectability of Flaws with a Coarse Measuring Grid and Air Coupled Ultrasound for NDT of Panel Materials Using the Re-Radiation Method. Appl. Sci. 2020, 10, 1155. [Google Scholar] [CrossRef] [Green Version]
- Schmelt, A.; Li, Z.; Marhenke, T.; Twiefel, J. Aussagefähigkeit von Fehlstellenimitaten in der ZfP. In Proceedings of the DAGA2020, Hannover, Germany, 16–19 March 2020; pp. 1133–1136. [Google Scholar]
- Schmelt, A.; Twiefel, J. The Spec-Radiation Method as a Fast Alternative to the Re-Radiation Method for the Detection of Flaws in Wooden Particleboards. Appl. Sci. 2020, 10, 6663. [Google Scholar] [CrossRef]
- Leseberg, D. Computer-generated three-dimensional image holograms. Appl. Opt. 1992, 31, 223–229. [Google Scholar] [CrossRef]
- Nicola, S.D.; Finizio, A.; Pierattini, G.; Ferraro, P.; Alfieri, D. Angular spectrum method with correction of anamorphism for numerical reconstruction of digital holograms on tilted planes. Opt. Express 2005, 13, 9935–9940. [Google Scholar] [CrossRef] [PubMed]
- Kostenka, J.; Kozacki, T.; Lizewski, K. Autofocusing method for tilted image plane detection in digital holographic microscopy. Opt. Commun. 2013, 297, 20–26. [Google Scholar] [CrossRef]
- Vilardy, J.M.; Jimenez, C.J.; Torres, C.O. Optical Image Encryption System Using Several Tilted Planes. Photonics 2019, 6, 116. [Google Scholar] [CrossRef] [Green Version]
- Matsushima, K. Introduction to Computer Holography; Springer Nature Switzerland AG: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; W. H. Freeman and Company: New York, NY, USA, 2017. [Google Scholar]
- Liu, D.L.; Waag, R.C. Propagation and backpropagation for ultrasonic wavefront design. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1997, 44, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Cramer, O. The variation of the specific heat ratio and the speed of sound in air with temperature, pressure, humidity, and CO2 concentration. J. Acoust. Soc. Am. 1993, 93, 2510–2516. [Google Scholar] [CrossRef]
- Wolf, E. Three-dimensional structure determination of semi-transparent objects from holographic data. Opt. Commun. 1969, 1, 153–156. [Google Scholar] [CrossRef]

















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmelt, A.S.; Twiefel, J. Flaw Detection on a Tilted Particleboard by Use of the Spec-Radiation Method. Appl. Sci. 2020, 10, 8513. https://doi.org/10.3390/app10238513
Schmelt AS, Twiefel J. Flaw Detection on a Tilted Particleboard by Use of the Spec-Radiation Method. Applied Sciences. 2020; 10(23):8513. https://doi.org/10.3390/app10238513
Chicago/Turabian StyleSchmelt, Andreas Sebastian, and Jens Twiefel. 2020. "Flaw Detection on a Tilted Particleboard by Use of the Spec-Radiation Method" Applied Sciences 10, no. 23: 8513. https://doi.org/10.3390/app10238513
APA StyleSchmelt, A. S., & Twiefel, J. (2020). Flaw Detection on a Tilted Particleboard by Use of the Spec-Radiation Method. Applied Sciences, 10(23), 8513. https://doi.org/10.3390/app10238513