Remaining Useful Strength (RUS) Prediction of SiCf-SiCm Composite Materials Using Deep Learning and Acoustic Emission
Abstract
:1. Introduction
- (1)
- We use expert-engineered features of AE signals to train a RF model so as to learn the patterns of the generated AE sound events from SiCf-SiCm materials for RUS prediction during their degradation.
- (2)
- We employ the raw AE signals to train two types of end-to-end deep CNN models, thus extracting high-level features from AE events, to achieve better RUS prediction performance and ensure better monitoring of the deterioration process of the test tubes of SiCf-SiCm.
- (3)
- We provide a comprehensive analysis of the models’ performance at predicting the RUS of SiCf-SiCm materials based on nine different experiments leading.
2. Materials and Methods
2.1. Dataset
2.2. Methods
2.3. Random-Forest
- The subset of the data used for training will be separated into multiple chunks of data based on the bootstrap aggregation method, which is a technique for separating a data set into multiple subsets in a uniform fashion and with replacement.
- Then for each data chunk, a regression decision tree is built. Then all these trees are combined together to make ensemble predictions.
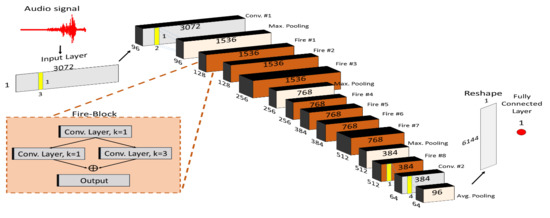
2.4. Convolutional Neural Networks
3. Results and Discussion
- Method-1: random-forest model trained with the 15 expert-selected features;
- Method-2: simple standard CNN model trained with the AE signals;
- Method-3: SqueezeNet based model trained with the AE signals.
- The RF model provided a better prediction of RUS for the earliest acoustic emission signals.
- The CNN models generally outperformed the RF model at predicting the RUS for signals, which occurred in the second half of the degradation process.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, H.; Li, S.; Cui, Y.; Liu, Z.; Yang, G.; Hu, J. Transfer Learning with Deep Recurrent Neural Networks for Remaining Useful Life Estimation. Appl. Sci. 2018, 8, 2416. [Google Scholar] [CrossRef] [Green Version]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Ren, L.; Cui, J.; Sun, Y.; Cheng, X. Multi-bearing remaining useful life collaborative prediction: A deep learning approach. J. Manuf. Syst. 2017, 43, 248–256. [Google Scholar] [CrossRef]
- Wu, Y.; Yuan, M.; Dong, S.; Lin, L.; Liu, Y. Remaining useful life estimation of engineered systems using vanilla LSTM neural networks. Neurocomputing 2018, 275, 167–179. [Google Scholar] [CrossRef]
- Babu, G.S.; Zhao, P.; Li, X.-L. Deep convolutional neural network based regression approach for estimation of remaining useful life. In Proceedings of the International Conference on Database Systems for Advanced Applications, Dallas, TX, USA, 16–19 April 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 214–228. [Google Scholar]
- Snead, L.; Nozawa, T.; Ferraris, M.; Katoh, Y.; Shinavski, R.; Sawan, M. Silicon carbide composites as fusion power reactor structural materials. J. Nucl. Mater. 2011, 417, 330–339. [Google Scholar] [CrossRef]
- Riccardi, B.; Giancarli, L.; Hasegawa, A.; Katoh, Y.; Kohyama, A.; Jones, R.; Snead, L. Issues and advances in SiCf/SiC composites development for fusion reactors. J. Nucl. Mater. 2004, 329, 56–65. [Google Scholar] [CrossRef]
- Alva, L.H. Monitoring The Progress of Damage in A SICf-SICm Composite Nuclear Fuel Cladding Under Internal Pressure Using Acoustic Emission. Ph.D. Thesis, Department of Mechanical Engineering, University of South Carolina, Columbia, SC, USA, 2018. [Google Scholar]
- Truesdale, N. Mechanical Characterization and Non-Destructive Evaluation of SiCF-SiCM Composite Tubing with the Impulse Excitation Technique. Ph.D. Thesis, Department of Mechanical Engineering, University of South Carolina, Columbia, SC, USA, 2017. [Google Scholar]
- Kumar, C.S.; Arumugam, V.; Santulli, C. Characterization of indentation damage resistance of hybrid composite laminates using acoustic emission monitoring. Compos. Part B Eng. 2017, 111, 165–178. [Google Scholar] [CrossRef]
- Whitlow, T.; Jones, E.; Przybyla, C. In-situ damage monitoring of a SiC/SiC ceramic matrix composite using acoustic emission and digital image correlation. Compos. Struct. 2016, 158, 245–251. [Google Scholar] [CrossRef]
- Appleby, M.; Zhu, D.; Morscher, G. Mechanical properties and real-time damage evaluations of environmental barrier coated SiC/SiC CMCs subjected to tensile loading under thermal gradients. Surf. Coat. Technol. 2015, 284, 318–326. [Google Scholar] [CrossRef] [Green Version]
- Alva, L.H.; Huang, X.; Jacobsen, G.M.; Back, C.A. High Pressure Burst Testing of SiC f-SiC m Composite Nuclear Fuel Cladding. In Advancement of Optical Methods in Experimental Mechanics; Springer: Berlin/Heidelberg, Germany, 2015; Volume 3, pp. 387–393. [Google Scholar]
- Shapovalov, K.; Jacobsen, G.M.; Alva, L.; Truesdale, N.; Deck, C.P.; Huang, X. Strength of SiCf-SiCm composite tube under uniaxial and multiaxial loading. J. Nucl. Mater. 2018, 500, 280–294. [Google Scholar] [CrossRef]
- Alva, L.; Shapovalov, K.; Jacobsen, G.M.; Back, C.A.; Huang, X. Experimental study of thermo-mechanical behavior of SiC composite tubing under high temperature gradient using solid surrogate. J. Nucl. Mater. 2015, 466, 698–711. [Google Scholar] [CrossRef] [Green Version]
- Von Stebut, J.; Lapostolle, F.; Bucsa, M.; Vallen, H. Acoustic emission monitoring of single cracking events and associated damage mechanism analysis in indentation and scratch testing. Surf. Coat. Technol. 1999, 116, 160–171. [Google Scholar] [CrossRef]
- Nasiri, A.; Bao, J.; Mccleeary, D.; Louis, S.-Y.M.; Huang, X.; Hu, J. Online Damage Monitoring of SiC f-SiC m Composite Materials Using Acoustic Emission and Deep Learning. IEEE Access 2019, 7, 140534–140541. [Google Scholar] [CrossRef]
- Ebrahimkhanlou, A.; Salamone, S. Single-sensor acoustic emission source localization in plate-like structures using deep learning. Aerospace 2018, 5, 50. [Google Scholar] [CrossRef] [Green Version]
- Elforjani, M.; Shanbr, S. Prognosis of bearing acoustic emission signals using supervised machine learning. IEEE Trans. Ind. Electron. 2017, 65, 5864–5871. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.; Jennings, C.; Terpenny, J.; Gao, R.X.; Kumara, S. A comparative study on machine learning algorithms for smart manufacturing: Tool wear prediction using random forests. J. Manuf. Sci. Eng. 2017, 139, 071018. [Google Scholar] [CrossRef]
- Piczak, K.J. Environmental sound classification with convolutional neural networks. In Proceedings of the 2015 IEEE 25th International Workshop on Machine Learning for Signal Processing (MLSP), Boston, MA, USA, 17–20 September 2015; pp. 1–6. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and < 0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]













| Feature ID | Definition |
|---|---|
| Feature 1 | Rise-Time |
| Feature 2 | Counts |
| Feature 3 | Energy |
| Feature 4 | Duration |
| Feature 5 | Amplitude |
| Feature 6 | Average Frequency |
| Feature 7 | Root Mean square (RMS) |
| Feature 8 | Average Signal Level (ASL) |
| Feature 9 | Counts to Peak |
| Feature 10 | Reverberation Frequency |
| Feature 11 | Initiation Frequency |
| Feature 12 | Signal Strength |
| Feature 13 | Absolute-Energy |
| Feature 14 | Frequency Centroid |
| Feature 15 | Peak Frequency |
| Count | Tube #1 | Tube #2 | Tube #3 | Tube #4 | Tube #5 | Tube #6 | Tube #7 | Tube #8 | Tube #9 |
|---|---|---|---|---|---|---|---|---|---|
| AE Events | 3286 | 4978 | 3869 | 6126 | 2893 | 2674 | 3590 | 3504 | 8919 |
| Method | Tube #1 | Tube #2 | Tube #3 | Tube #4 | Tube #5 | Tube #6 | Tube #7 | Tube #8 | Tube #9 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| RF | 3.3 | 4.03 | 3.21 | 3.26 | 4.99 | 4.60 | 2.98 | 2.33 | 4.63 | 3.70 |
| CNN-basic | 2.23 | 4.08 | 3.3 | 3.37 | 5.2 | 4.07 | 3.01 | 2.94 | 4.15 | 3.60 |
| CNN-squeeze | 2.13 | 4.09 | 2.81 | 3.56 | 5.51 | 4.1 | 3.07 | 2.64 | 4.02 | 3.55 |
| Method | Tube #1 | Tube 2 | Tube #3 | Tube #4 | Tube #5 | Tube #6 | Tube #7 | Tube #8 | Tube #9 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| RF | 0.72 | 0.81 | 0.79 | 0.8 | 0.82 | 0.84 | 0.79 | 0.93 | 0.70 | 0.80 |
| CNN-basic | 0.82 | 0.87 | 0.85 | 0.83 | 0.76 | 0.83 | 0.79 | 0.86 | 0.81 | 0.82 |
| CNN-squeeze | 0.84 | 0.9 | 0.88 | 0.79 | 0.79 | 0.86 | 0.79 | 0.87 | 0.83 | 0.85 |
| Stage # | Tube #1 | Tube #2 | Tube #3 | Tube #4 | Tube #5 | Tube #6 | Tube #7 | Tube #8 | Tube #9 |
|---|---|---|---|---|---|---|---|---|---|
| Stage-1 | 0.105 | 0.443 | 0.224 | 0.326 | 0.028 | 0.108 | 0.171 | 0.087 | 0.047 |
| Stage-2 | 0.74 | 1.206 | 1.14 | 0.717 | 0.826 | 0.652 | 0.744 | 1.295 | 0.587 |
| Stage-3 | 0.861 | 1.16 | 1.094 | 0.668 | 0.832 | 0.512 | 0.905 | 0.885 | 0.932 |
| Stage-4 | 1.163 | 0.739 | 0.706 | 0.431 | 0.725 | 0.807 | 0.578 | 0.357 | 0.638 |
| Stage-5 | 1.201 | 0.36 | 0.411 | 0.373 | 0.674 | 0.775 | 0.37 | 0.203 | 0.532 |
| Stage-6 | 0.994 | 0.201 | 0.338 | nan | 0.685 | 0.601 | nan | nan | 0.317 |
| Stage-7 | 0.85 | 0.186 | nan | nan | nan | 0.471 | nan | nan | 0.258 |
| Stage-8 | 0.657 | nan | nan | nan | nan | nan | nan | nan | 0.165 |
| Stage-9 | nan | nan | nan | nan | nan | nan | nan | nan | 0.136 |
| Stage-10 | nan | nan | nan | nan | nan | nan | nan | nan | 0.172 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Louis, S.-Y.M.; Nasiri, A.; Bao, J.; Cui, Y.; Zhao, Y.; Jin, J.; Huang, X.; Hu, J. Remaining Useful Strength (RUS) Prediction of SiCf-SiCm Composite Materials Using Deep Learning and Acoustic Emission. Appl. Sci. 2020, 10, 2680. https://doi.org/10.3390/app10082680
Louis S-YM, Nasiri A, Bao J, Cui Y, Zhao Y, Jin J, Huang X, Hu J. Remaining Useful Strength (RUS) Prediction of SiCf-SiCm Composite Materials Using Deep Learning and Acoustic Emission. Applied Sciences. 2020; 10(8):2680. https://doi.org/10.3390/app10082680
Chicago/Turabian StyleLouis, Steph-Yves M., Alireza Nasiri, Jingjing Bao, Yuxin Cui, Yong Zhao, Jing Jin, Xinyu Huang, and Jianjun Hu. 2020. "Remaining Useful Strength (RUS) Prediction of SiCf-SiCm Composite Materials Using Deep Learning and Acoustic Emission" Applied Sciences 10, no. 8: 2680. https://doi.org/10.3390/app10082680
APA StyleLouis, S. -Y. M., Nasiri, A., Bao, J., Cui, Y., Zhao, Y., Jin, J., Huang, X., & Hu, J. (2020). Remaining Useful Strength (RUS) Prediction of SiCf-SiCm Composite Materials Using Deep Learning and Acoustic Emission. Applied Sciences, 10(8), 2680. https://doi.org/10.3390/app10082680