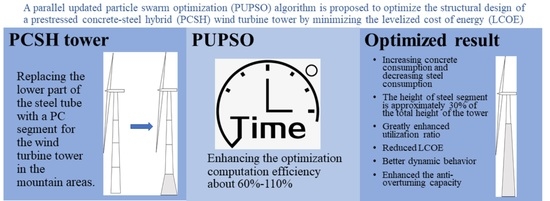
Hybrid Wind Turbine Towers Optimization with a Parallel Updated Particle Swarm Algorithm
Abstract
:1. Introduction
2. Effects of Wind and Earthquake Excitations on Wind Turbine Tower
2.1. Wind Load Applied to the PCSH Wind Turbine Towers
2.1.1. Aerodynamic Load Determination
2.1.2. Pitching Moment
2.1.3. Deflecting Torque
2.2. Wind Load Acting on the Tower
2.3. Additional Bending Moment
2.4. Earthquake Effect
2.5. Load Combination
3. Design Constraints for Optimization of the PCSH Tower
3.1. Constraints on the Steel Tubular Segment
3.1.1. Local Buckling
3.1.2. Overall Stability
3.1.3. Load-Carrying Capacity
3.1.4. Fatigue
3.2. Constraints on the PC Segments
3.2.1. Load-Carrying Capacity
3.2.2. Fatigue
3.2.3. Geometry Constraint
3.3. Other Constraints
3.3.1. Natural Frequency
3.3.2. Maximum Top Displacement
4. PUPSO Approach with the Objective Function of LCOE
4.1. Updated Partial Swarm Optimization (UPSO) Approach
- 1.
- Weight function’s learning factor
- 2.
- Random perturbation
4.2. Objective Function
4.3. Optimization Variables
4.4. Flow Chart of PUPSO Algorithm
5. Optimization for PCSH Wind Turbine Tower
5.1. Design Parameters
5.2. Optimization Results for the PCSH Wind Turbine Tower
5.2.1. LCOE Optimization
5.2.2. Utilization Ratio Comparison
5.2.3. Fundamental Natural Frequency Comparison
5.2.4. Weight Comparison
5.2.5. Computation Efficiency Comparison
6. Conclusions
- 1.
- The proposed PUPSO algorithm performs better when compared with the traditional PSO algorithm and the UPSO. The computation time is greatly reduced by using parallel algorithms. Fulfilling the design constraints of relevant specifications and industry standards, the PUPSO algorithm provides an optimal design for the PCSH wind turbine towers with considerably improved computational efficiency.
- 2.
- The levelized cost of energy (LCOE) of the PCSH wind turbine tower in a life cycle perspective is considered as the objective function as an alternative to the direct investment. The LCOE of the optimized PCSH wind turbine clearly decreases when compared with the benchmark tower and increases the material utilization rate of the tower. The optimized PCSH wind turbine tower can be an economic alternative for wind farms with lower LCOE requirements. The height of the steel segment of the optimized PUPSO tower is recommended to be 30% of the total height of the PCSH wind turbine tower.
- 3.
- The optimized tower can provide better dynamic behavior to avoid the resonance caused by wind turbine excitation.
- 4.
- The optimization results for PCSH wind turbine towers provide valuable references in practice for PCSH wind turbine tower design in mountainous areas. This paper, based on a linear hypothesis and limited deformation, has been conducted as the preliminary optimization. Because of the nonlinearity present in prestressed concrete towers, nonlinear calculations should be investigated in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Quilligan, A.; O’Connor, A.; Pakrashi, V. Fragility analysis of steel and concrete wind turbine towers. Eng. Struct. 2012, 36, 270–282. [Google Scholar] [CrossRef]
- Lantz, E.; Roberts, O.; Nunemaker, J.; Edgar, D.; Dykes, K.; Scott, G. Increasing Wind Turbine Tower Heights: Opportunities and Challenges; National Renewable Energy Laboratory (NREL): Denver, CO, USA, 2019. [Google Scholar]
- Yadav, K.K.; Gerasimidis, S. Instability of thin steel cylindrical shells under bending. Thin Walled Struct. 2019, 137, 151–166. [Google Scholar] [CrossRef]
- Yadav, K.K.; Gerasimidis, S. Imperfection insensitive thin cylindrical shells for next generation wind turbine towers. J. Constr. Steel Res. 2020, 172, 106228. [Google Scholar] [CrossRef]
- de Lana, J.A.; Júnior, P.A.A.M.; Magalhães, C.A.; Magalhães, A.L.M.A.; de Andrade Junior, A.C.; de Barros Ribeiro, M.S. Behavior study of prestressed concrete wind-turbine tower in circular cross-section. Eng. Struct. 2021, 227, 111403. [Google Scholar] [CrossRef]
- Jay, A.; Myers, A.T.; Torabian, S.; Mahmoud, A.; Smith, E.; Agbayani, N.; Schafer, B.W. Spirally welded steel wind towers: Buckling experiments, analyses, and research needs. J. Constr. Steel Res. 2016, 125, 218–226. [Google Scholar] [CrossRef] [Green Version]
- Singh, A. Concrete construction for wind energy towers. Indian Concr. J. 2007, 81, 43–49. [Google Scholar]
- Seidel, M. Experiences with two of the world’s largest wind turbine towers. In Proceedings of the 2003 EWEC European Wind Energy Conference and Exhibition, Madrid, Spain, 6–19 June 2003; pp. 16–19. [Google Scholar]
- Kaveh, A.; Ghazaan, M.I. Meta-Heuristic Algorithms for Optimal Design of Real-Size Structures; Springer: Cham, Switzerland, 2018; pp. 5–6. [Google Scholar]
- Negm, H.M.; Maalawi, K.Y. Structural design optimization of wind turbine towers. Comput. Struct. 2000, 74, 649–666. [Google Scholar] [CrossRef]
- Uys, P.; Farkas, J.; Jarmai, K.; Van Tonder, F. Optimisation of a steel tower for a wind turbine structure. Eng. Struct. 2007, 29, 1337–1342. [Google Scholar] [CrossRef]
- Nicholson, J.C. Design of Wind Turbine Tower and Foundation Systems: Optimization Approach; The University of Iowa: Iowa City, IA, USA, 2011. [Google Scholar]
- Nicholson, J.C.; Arora, J.S.; Goyal, D.; Tinjum, J.M. Multi-Objective Structural Optimization of Wind Turbine Tower and Foundation Systems using Isight: A Process Automation and Design Exploration Software. In Proceedings of the 10th World Congress on Structural and Multidisciplinary Optimization, Orlando, FL, USA, 19–24 May 2013; pp. 1–10. [Google Scholar]
- Ma, H.; Meng, R. Optimization design of prestressed concrete wind-turbine tower. Sci. China Technol. Sci. 2014, 57, 414–422. [Google Scholar] [CrossRef]
- Oest, J.; Sandal, K.; Schafhirt, S.; Stieng, L.E.S.; Muskulus, M. On gradient-based optimization of jacket structures for offshore wind turbines. Wind Energy 2018, 21, 953–967. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; He, X. Design optimization of steel–concrete hybrid wind turbine tower based on improved genetic algorithm. Struct. Des. Tall Spec. Build. 2020, 29, e1741. [Google Scholar] [CrossRef]
- Sahib, N.M.; Hussein, A. Particle Swarm Optimization in Managing Construction Problems. Procedia Comput. Sci. 2019, 154, 260–266. [Google Scholar] [CrossRef]
- Poitras, G.; Lefrançois, G.; Cormier, G. Optimization of steel floor systems using particle swarm optimization. J. Constr. Steel Res. 2011, 67, 1225–1231. [Google Scholar] [CrossRef]
- Ye, J.; Hajirasouliha, I.; Becque, J.; Eslami, A. Optimum design of cold-formed steel beams using Particle Swarm Optimisation method. J. Constr. Steel Res. 2016, 122, 80–93. [Google Scholar] [CrossRef] [Green Version]
- Luo, L.; He, W.; Zhang, X. PSO-Based Approach for Buckling Analysis of Shell Structures with Geometric Imperfections. Math. Probl. Eng. 2019, 2019, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Zhang, T.-Y.; Huang, W.; Hu, M.-Y.; Qin, J.-W.; Zu, X.-C. Active control for machinery equipment induced structural vibration using H∞ criterion and PSO technique. Eng. Rev. 2019, 39, 21–28. [Google Scholar] [CrossRef]
- Tsiptsis, I.N.; Liimatainen, L.; Kotnik, T.; Niiranen, J. Structural optimization employing isogeometric tools in Particle Swarm Optimizer. J. Build. Eng. 2019, 24, 100761. [Google Scholar] [CrossRef]
- Moradi, S.; Vosoughi, A.R.; Anjabin, N. Maximum buckling load of stiffened laminated composite panel by an improved hybrid PSO-GA optimization technique. Thin-Walled Struct. 2021, 160, 107382. [Google Scholar] [CrossRef]
- Kaveh, A.; Eslamlou, A.D. Metaheuristic Optimization Algorithms in Civil Engineering: New Applications; Springer: Cham, Switzerland, 2020; pp. 24–34. [Google Scholar]
- Niu, J. Research on the Structural Performance of Prestressed Concrete-Steel Hybrid Wind Turbine Tower. Master’s Thesis, Hunan University, Changsha, China, 2014. [Google Scholar]
- Chen, X. Static loads and dynamic loads of wind turbine tower. Wind Power Gener. 1989, 3, 44–49. [Google Scholar]
- Zhao, W.; Cao, P.; Chen, J. The Research of Load Calculation Method and Loads Combination about Wind Turbine Tower. Spec. Struct. 2020, 4, 80–83. [Google Scholar]
- SAC. GB50009-2012: Load Code for the Design of Building Structures; Standardization Administration of China: Beijing, China, 2012.
- Dai, K.; Wang, Y.; Huang, Y.; Zhu, W.D.; Xu, Y.F. A Modified Stochastic Subspace Identification Method for Estimating Natural Frequencies. In Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition, Phoenix, Arizona, USA, 11–17 November 2016. [Google Scholar]
- Ma, H.; Zhang, D. Seismic Response of a Prestressed Concrete Wind Turbine Tower. Int. J. Civ. Eng. 2016, 14, 1–11. [Google Scholar] [CrossRef]
- SAC. GB 50011-2010: Code for Seismic Design of Buildings; Standardization Administration of China: Beijing, China, 2010.
- LaNier, M.W. LWST Phase I Project Conceptual Design Study: Evaluation of Design and Construction Approaches for Economical Hybrid Steel/Concrete Wind Turbine Towers; 28 June 2002–31 July 2004; National Renewable Energy Lab.: Golden, CO, USA, 2005. [Google Scholar] [CrossRef] [Green Version]
- He, Y.-S.; Wang, J.; Zhao, H.-Y.; Li, Z.-L.; Xing, K.; Yao, S.; Zeng-Jun, H. Research of load calculation and load combination for wind turbine generator system of beach-shallow sea. Build. Sci. 2012, 120–127. [Google Scholar]
- SAC. GB 50051-2013: Code for Design of Chimneys; Standardization Administration of China: Beijing, China, 2013.
- SAC. GB 50017-2017: Code for Design of Steel Structure; Standardization Administration of China: Beijing, China, 2017.
- Agbayani, N.A. A Technical Overview of ASCE/AWEA RP2011: Recommended Practice for Compliance of Large Land-Based Wind Turbine Support Structures. In Proceedings of the Structures Congress 2014, Boston, MA, USA, 3–5 April 2014; pp. 1759–1770. [Google Scholar]
- Justus, C.; Hargraves, W.; Mikhail, A.; Graber, D. Methods for estimating wind speed frequency distributions. J. Appl. Meteorol. 1978, 17, 350–353. [Google Scholar] [CrossRef]
- Huo, T.; Tong, L. An approach to wind-induced fatigue analysis of wind turbine tubular towers. J. Constr. Steel Res. 2020, 166, 105917. [Google Scholar] [CrossRef]
- SAC. GB 50135-2006: Code for Design of High-Rising Structures; Standardization Administration of China: Beijing, China, 2007.
- SAC. GB 50010-2010: Code for Design of Concrete Structures; Standardization Administration of China: Beijing, China, 2010.
- Grünberg, J.; Göhlmann, J. Concrete Structures for Wind Turbines; John Wiley & Sons: Berlin, Germany, 2013. [Google Scholar]
- Liu, X. Introduction to Artificial Intelligence: Approaches and Systems; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Zhao, Y.; Fang, Z. Particle swarm optimization algorithm with weight function’s learning factor. J. Comput. Appl. 2013, 33, 2265–2268. [Google Scholar] [CrossRef]
- Bruck, M.; Sandborn, P.; Goudarzi, N. A Levelized Cost of Energy (LCOE) Model for Wind Farms that Includes Power Purchase Agreement (PPA) Energy Delivery Limits. Renew. Energy 2016, 122, 131–139. [Google Scholar] [CrossRef]
- Myhr, A.; Bjerkseter, C.; Ågotnes, A.; Nygaard, T.A. Levelised cost of energy for offshore floating wind turbines in a life cycle perspective. Renew. Energy 2014, 66, 714–728. [Google Scholar] [CrossRef] [Green Version]
- Khojasteh, H.; Noorollahi, Y.; Tahani, M.; Masdari, M. Optimization of Power and Levelized Cost for Shrouded Small Wind Turbine. Inventions 2020, 5, 59. [Google Scholar] [CrossRef]
- Product Introduction of XE93-2000. Available online: http://wp.china-nengyuan.com/member_product/21420.html (accessed on 20 April 2021).








| Load Combinations | Load Factors |
|---|---|
| Ultimate 1 | |
| Ultimate 2 | |
| Service 1 | |
| Service 2 |
| Title | Item | Unit Price |
|---|---|---|
| Direct cost | Concrete | 600 yuan/m3 |
| Reinforcement | 5500 yuan/ton | |
| Prestressing steel strand | 14,390 yuan/ton | |
| Sheeting | 50 yuan/m2 | |
| Timber support | 15 yuan/m2 | |
| Metallic pipe | 679 yuan/100 m | |
| Flange | 40,000 yuan/pcs | |
| Q345 | 1000 yuan/ton | |
| Labor cost and mechanical cost | Reinforcement | 1500 yuan/ton |
| Prestressing steel strand | 1000 yuan/ton | |
| Sheeting | 300 yuan/100 m2 | |
| Timber support | 15 yuan/m2 | |
| concrete | 60 yuan/m3 | |
| Project condition | Installed capacity | 50 MW |
| Equipment fee | 5200 yuan/kW | |
| Other cost | 1200 yuan/kW | |
| Annual cost during operation | 80 yuan/kW (Year 1–5) | |
| 120 yuan/kW (Year 6–20) | ||
| construction period | 1 a | |
| Loan-to-value ratio | 80% | |
| Depreciation life | 20 a | |
| Ratio of remaining value | 5% | |
| Length of maturity | 15 a | |
| Interest rate | 4.9% |
| Variable | Range |
|---|---|
| Length of the steel section (mm) | 500–70,000 |
| Thickness of the steel section (mm) | 10–25 |
| Outer diameter of the top end of the steel section | 2686 (j = 1) |
| (j > 1) | |
| Outer diameter of the bottom end of the steel section | |
| Steel segments | 1–3 |
| Length of the concrete section | 7500– |
| Thickness of the top end of the concrete part (mm) | 180–500 |
| Thickness of the bottom end of the concrete part (mm) | -500 |
| Outer diameter of the top end of the concrete part (mm) | - |
| Outer diameter of the bottom end of the concrete part (mm) | |
| Area of prestressed reinforcement (mm2) | 31,150–62,300 |
| Wind Turbine Parameters | Value |
|---|---|
| Generator model | XE93-2000 |
| Rated power | 2 MW |
| Rotor diameter | 93.4 m |
| Nacelle and hub weight | 80 t |
| Distance from gravitational center of the nacelle and hub to the center of tower | 3000 mm |
| Weight of blades | 48.5 t |
| Distance from gravitational center of the blades to the center of tower | 4864 mm |
| IEC wind zone | IECIIIA |
| Annual average wind speed | 7.5 m/s |
| Cut-in wind speed | 3 m/s |
| Nominal wind speed | 11 m/s |
| Cut-out wind speed | 25 m/s |
| Extreme wind speed | 52.5 m/s |
| Rotational speed | 23 rpm |
| Maximum turbulence intensity | 0.18 |
| Parameter | Value |
|---|---|
| 0.9 | |
| 0.4 | |
| 50 | |
| 30 | |
| Penalty term | 0.5 |
| 0.3 |
| Category | Equivalent Available Duration (h) | Electricity Price in 2019 (Yuan/kWh) | LCOE for the Benchmark PCSH Tower (Yuan/kWh) | LCOE for the Optimized PCSH Tower (Yuan/kWh) |
|---|---|---|---|---|
| I | 2850 | 0.34 | 0.3613 | 0.3474 |
| II | 2600 | 0.39 | 0.3874 | 0.3722 |
| III | 2500 | 0.43 | 0.3993 | 0.3835 |
| IV | 2000 | 0.52 | 0.4769 | 0.4571 |
| Tower | Variable | Before Optimization | After Optimization |
|---|---|---|---|
| Steel tube segment | Segment | 3 | 1 |
| (mm) | 14 | 10 | |
| (mm) | 2686 | 2686 | |
| (mm) | 3485 | 3296 | |
| (mm) | 21,500 | 22,000 | |
| (mm) | 18 | - | |
| (mm) | 3485 | - | |
| (mm) | 4046 | - | |
| (mm) | 20,000 | - | |
| (mm) | 20 | - | |
| (mm) | 4046 | - | |
| (mm) | 4400 | - | |
| (mm) | 20,000 | - | |
| PC segment | (mm) | 500 | 270 |
| (mm) | 500 | 285 | |
| (mm) | 16,000 | 55,500 | |
| (mm) | 4878 | 3549 | |
| (mm) | 6900 | 5800 | |
| Prestressed duct number | 36 | 36 | |
| Prestressed reinforcement | 81 × 7 (d = 15.2 mm) | 71 × 7 (d = 12.7 mm) | |
| Prestressed reinforcement area (mm2) | 40,320 | 24,872 |
| Tower | Maximum Utilization Ratio | Before Optimization | After Optimization |
|---|---|---|---|
| Steel segment | Local buckling | 0.45 | 0.84 |
| Overall stability | 0.40 | 0.52 | |
| Compressive load-carrying capacity | 0.53 | 0.76 | |
| Shear load-carrying capacity | 0.15 | 0.37 | |
| Torsion load-carrying capacity | 0.00075 | 0.0013 | |
| Combined load-carrying capacity | 0.29 | 0.67 | |
| Fatigue | 0.41 | 0.52 | |
| PC segment | Load-carrying capacity of windward side | 0.064 | 0.34 |
| Load-carrying capacity of leeward side | 0.48 | 0.25 | |
| Combined load-carrying capacity | 0.091 | 0.45 | |
| Fatigue of windward side | 0.56 | 0.94 | |
| Fatigue of leeward side | 0.21 | 0.48 | |
| Fatigue of prestressing bar | 0.93 | 0.91 |
| Tower | Frequency (Hz) |
|---|---|
| Before optimization | 0.45 |
| After optimization | 0.56 |
| Weight | Before Optimization | After Optimization |
|---|---|---|
| Steel segment (t) | 90 | 16 |
| PC segment (t) | 338 | 528 |
| Total (t) | 428 | 544 |
| Cycle Number | PSO Computation (s) | UPSO Computation (s) | PUPSO Computation (s) |
|---|---|---|---|
| 5 | 55,074 | 44,912 | 27,845 |
| 10 | 99,352 | 107,553 | 52,427 |
| PSO Computation (s) | UPSO Computation (s) | PUPSO Computation (s) |
|---|---|---|
| 432,759 | 451,480 | 212,801 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chen, H.; Xu, B.; Ge, H. Hybrid Wind Turbine Towers Optimization with a Parallel Updated Particle Swarm Algorithm. Appl. Sci. 2021, 11, 8683. https://doi.org/10.3390/app11188683
Li Z, Chen H, Xu B, Ge H. Hybrid Wind Turbine Towers Optimization with a Parallel Updated Particle Swarm Algorithm. Applied Sciences. 2021; 11(18):8683. https://doi.org/10.3390/app11188683
Chicago/Turabian StyleLi, Zeyu, Hongbing Chen, Bin Xu, and Hanbin Ge. 2021. "Hybrid Wind Turbine Towers Optimization with a Parallel Updated Particle Swarm Algorithm" Applied Sciences 11, no. 18: 8683. https://doi.org/10.3390/app11188683
APA StyleLi, Z., Chen, H., Xu, B., & Ge, H. (2021). Hybrid Wind Turbine Towers Optimization with a Parallel Updated Particle Swarm Algorithm. Applied Sciences, 11(18), 8683. https://doi.org/10.3390/app11188683