A Theoretical Analysis of Magnetic Particle Alignment in External Magnetic Fields Affected by Viscosity and Brownian Motion
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Physical Model
2.2. Solution
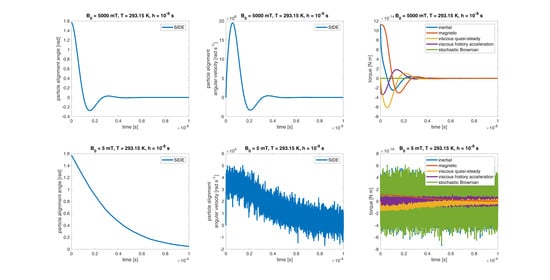
3. Results and Discussion
3.1. Comparison of Models
3.2. Strong Field Limit Case
3.3. Weak Field Limit Case
3.4. Characteristic Time of Magnetic Particle Alignment
3.5. Limitations
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DEs | System of differential equations |
| IDEs | System of integro-differential equations |
| MPI | Magnetic particle imaging |
| MRI | Magnetic resonance imaging |
| ODEs | System of ordinary differential equations |
| SDEs | System of stochastic differential equations |
| SIDEs | System of stochastic integro-differential equations |
References
- Dames, P.; Gleich, B.; Flemmer, A.; Hajek, K.; Seidl, N.; Wiekhorst, F.; Eberbeck, D.; Bittmann, I.; Bergemann, C.; Weyh, T.; et al. Targeted delivery of magnetic aerosol droplets to the lung. Nat. Nanotechnol. 2007, 2, 495–499. [Google Scholar] [CrossRef] [PubMed]
- Krafcik, A.; Babinec, P.; Frollo, I. Computational analysis of magnetic field induced deposition of magnetic particles in lung alveolus in comparison to deposition produced with viscous drag and gravitational force. J. Magn. Magn. Mater. 2015, 380, 46–53. [Google Scholar] [CrossRef]
- Surendran, A.; Zhou, R.; Lin, Y. Microfluidic Devices for Magnetic Separation of Biological Particles: A Review. J. Med. Devices Trans. ASME 2021, 15, 024001. [Google Scholar] [CrossRef]
- Babinec, P.; Krafcik, A.; Babincova, M.; Rosenecker, J. Dynamics of magnetic particles in cylindrical Halbach array: Implications for magnetic cell separation and drug targeting. Med. Biol. Eng. Comput. 2010, 48, 745–753. [Google Scholar] [CrossRef]
- Krafcik, A.; Babinec, P.; Babincova, M.; Frollo, I. High gradient magnetic separation with involved Basset history force: Configuration with single axial wire. Powder Technol. 2019, 347, 50–58. [Google Scholar] [CrossRef]
- Perigo, E.A.; Hemery, G.; Sandre, O.; Ortega, D.; Garaio, E.; Plazaola, F.; Teran, F.J. Fundamentals and advances in magnetic hyperthermia. Appl. Phys. Rev. 2015, 2, 041302. [Google Scholar] [CrossRef] [Green Version]
- Babincova, N.; Sourivong, P.; Babinec, P.; Bergemann, C.; Babincova, M.; Durdik, S. Applications of magnetoliposomes with encapsulated doxorubicin for integrated chemotherapy and hyperthermia of rat C6 glioma. Z. Naturforsch. Sect. C J. Biosci. 2018, 73, 265–271. [Google Scholar] [CrossRef]
- Saritas, E.; Goodwill, P.; Croft, L.; Konkle, J.; Lu, K.; Zheng, B.; Conolly, S. Magnetic particle imaging (MPI) for NMR and MRI researchers. J. Magn. Reson. 2013, 229, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Strbak, O.; Antal, I.; Khmara, I.; Koneracka, M.; Kubovcikova, M.; Zavisova, V.; Molcan, M.; Jurikova, A.; Hnilicova, P.; Gombos, J.; et al. Influence of dextran molecular weight on the physical properties of magnetic nanoparticles for hyperthermia and MRI applications. Nanomaterials 2020, 10, 2468. [Google Scholar] [CrossRef]
- Strbak, O.; Balejcikova, L.; Kmetova, M.; Gombos, J.; Kovac, J.; Dobrota, D.; Kopcansky, P. Longitudinal and transverse relaxivity analysis of native ferritin and magnetoferritin at 7 T MRI. Int. J. Mol. Sci. 2021, 22, 8487. [Google Scholar] [CrossRef]
- Koksharov, Y.A. Magnetism of Nanoparticles: Effects of Size, Shape, and Interactions. In Magnetic Nanoparticles; Gubin, S.P., Ed.; John Wiley & Sons, Ltd.: Weinheim, Germany, 2009; Chapter 6; pp. 197–254. [Google Scholar] [CrossRef]
- Dieckhoff, J.; Eberbeck, D.; Schilling, M.; Ludwig, F. Magnetic-field dependence of Brownian and Néel relaxation times. J. Appl. Phys. 2016, 119, 043903. [Google Scholar] [CrossRef]
- Croft, L.; Goodwill, P.; Ferguson, M.; Krishnan, K.; Conolly, S. Relaxation in x-space magnetic particle imaging. Springer Proc. Phys. 2012, 140, 149–153. [Google Scholar] [CrossRef] [Green Version]
- Estelrich, J.; Sanchez-Martín, M.; Busquets, M. Nanoparticles in magnetic resonance imaging: From simple to dual contrast agents. Int. J. Nanomed. 2015, 10, 1727–1741. [Google Scholar] [CrossRef] [Green Version]
- Paysen, H.; Loewa, N.; Weber, K.; Kosch, O.; Wells, J.; Schaeffter, T.; Wiekhorst, F. Imaging and quantification of magnetic nanoparticles: Comparison of magnetic resonance imaging and magnetic particle imaging. J. Magn. Magn. Mater. 2019, 475, 382–388. [Google Scholar] [CrossRef]
- Nishimoto, K.; Ota, S.; Shi, G.; Takeda, R.; Trisnanto, S.; Yamada, T.; Takemura, Y. High intrinsic loss power of multicore magnetic nanoparticles with blood-pooling property for hyperthermia. AIP Adv. 2019, 9, 035347. [Google Scholar] [CrossRef]
- Manzin, A.; Ferrero, R.; Vicentini, M. From Micromagnetic to In Silico Modeling of Magnetic Nanodisks for Hyperthermia Applications. Adv. Theory Simul. 2021, 4, 2100013. [Google Scholar] [CrossRef]
- Chandrasekharan, P.; Tay, Z.; Hensley, D.; Zhou, X.; Fung, B.; Colson, C.; Lu, Y.; Fellows, B.; Huynh, Q.; Saayujya, C.; et al. Using magnetic particle imaging systems to localize and guide magnetic hyperthermia treatment: Tracers, hardware, and future medical applications. Theranostics 2020, 10, 2965–2981. [Google Scholar] [CrossRef] [PubMed]
- Gauger, A.; Hershberger, K.; Bronstein, L. Theranostics Based on Magnetic Nanoparticles and Polymers: Intelligent Design for Efficient Diagnostics and Therapy. Front. Chem. 2020, 8, 561. [Google Scholar] [CrossRef]
- Hensley, D.; Tay, Z.; Dhavalikar, R.; Zheng, B.; Goodwill, P.; Rinaldi, C.; Conolly, S. Combining magnetic particle imaging and magnetic fluid hyperthermia in a theranostic platform. Phys. Med. Biol. 2017, 62, 3483–3500. [Google Scholar] [CrossRef]
- Lange, J.; Kotitz, R.; Haller, A.; Trahms, L.; Semmler, W.; Weitschies, W. Magnetorelaxometry—A new binding specific detection method based on magnetic nanoparticles. J. Magn. Magn. Mater. 2002, 252, 381–383. [Google Scholar] [CrossRef]
- Jaufenthaler, A.; Schultze, V.; Scholtes, T.; Schmidt, C.; Handler, M.; Stolz, R.; Baumgarten, D. OPM magnetorelaxometry in the presence of a DC bias field. EPJ Quantum Technol. 2020, 7, 12. [Google Scholar] [CrossRef]
- Smith, M.; Sheehan, P.; Perry, L.; O’Connor, K.; Csonka, L.; Applegate, B.; Whitman, L. Quantifying the magnetic advantage in magnetotaxis. Biophys. J. 2006, 91, 1098–1107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bennet, M.A.; Eder, S.H.K. Magnetoreception and Magnetotaxis. In Iron Oxides: From Nature to Applications; Faivre, D., Ed.; John Wiley & Sons, Ltd.: Weinheim, Germany, 2016; Chapter 22; pp. 567–590. [Google Scholar] [CrossRef]
- Satyanarayana, S.; Padmaprahlada, S.; Chitradurga, R.; Bhattacharya, S. Orientational dynamics of magnetotactic bacteria in Earth’s magnetic field—A simulation study. J. Biol. Phys. 2021, 47, 79–93. [Google Scholar] [CrossRef]
- Erglis, K.; Wen, Q.; Ose, V.; Zeltins, A.; Sharipo, A.; Janmey, P.; Cebers, A. Dynamics of magnetotactic bacteria in a rotating magnetic field. Biophys. J. 2007, 93, 1402–1412. [Google Scholar] [CrossRef] [Green Version]
- Lohmann, K. QA: Animal behaviour: Magnetic-field perception. Nature 2010, 464, 1140–1142. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Box, F.; Thompson, A.; Mullin, T. Torsional oscillations of a sphere in a Stokes flow. Exp. Fluids 2015, 56, 209. [Google Scholar] [CrossRef] [Green Version]
- Lei, U.; Yang, C.; Wu, K. Viscous torque on a sphere under arbitrary rotation. Appl. Phys. Lett. 2006, 89, 181908. [Google Scholar] [CrossRef]
- Basset, A.B.; Strutt, J.W., III. On the motion of a sphere in a viscous liquid. Philos. Trans. R. Soc. A 1888, 179, 43–63. [Google Scholar] [CrossRef] [Green Version]
- Premlata, A.; Wei, H.H. Atypical non-Basset particle dynamics due to hydrodynamic slip. Phys. Fluids 2020, 32, 097109. [Google Scholar] [CrossRef]
- Romodina, M.; Lyubin, E.; Fedyanin, A. Detection of Brownian Torque in a Magnetically-Driven Rotating Microsystem. Sci. Rep. 2016, 6, 21212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Helgesen, G.; Pieranski, P.; Skjeltorp, A. Nonlinear phenomena in systems of magnetic holes. Phys. Rev. Lett. 1990, 64, 1425–1428. [Google Scholar] [CrossRef]
- McNaughton, B.; Agayan, R.; Wang, J.; Kopelman, R. Physiochemical microparticle sensors based on nonlinear magnetic oscillations. Sens. Actuators B Chem. 2007, 121, 330–340. [Google Scholar] [CrossRef]
- Tierno, P.; Claret, J.; Sagues, F.; Cabers, A. Overdamped dynamics of paramagnetic ellipsoids in a precessing magnetic field. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 79, 021501. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Yamaguchi, M.; Ozawa, S.; Yamamoto, I. Rotational diffusion model of magnetic alignment. Jpn. J. Appl. Phys. 2009, 48, 063001. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Ozawa, S.; Yamamoto, I.; Kimura, T. Characterization of three-dimensional magnetic alignment for magnetically biaxial particles. Jpn. J. Appl. Phys. 2013, 52, 013003. [Google Scholar] [CrossRef]
- Ilyin, V.; Procaccia, I.; Zagorodny, A. Stochastic processes crossing from ballistic to fractional diffusion with memory: Exact results. Condens. Matter Phys. 2010, 13, 23001–23008. [Google Scholar] [CrossRef] [Green Version]
- Jones, R.B. Rotational Diffusion in Dispersive Media; Centre of Excellence for Advanced Materials and Structures: Warsaw, Poland, 2003. [Google Scholar]
- Volpe, G.; Volpe, G. Simulation of a Brownian particle in an optical trap. Am. J. Phys. 2013, 81, 224–230. [Google Scholar] [CrossRef] [Green Version]
- Tothova, J.; Vasziova, G.; Glod, L.; Lisy, V. Langevin theory of anomalous Brownian motion made simple. Eur. J. Phys. 2011, 32, 645–655. [Google Scholar] [CrossRef]
- Tothova, J.; Vasziov, G.; Glod, L.; Lisy, V. A note on ‘Langevin theory of anomalous Brownian motion made simple’. Eur. J. Phys. 2011, 32, L04. [Google Scholar] [CrossRef]
- Tothova, J.; Lisy, V. Generalized Langevin theory of the Brownian motion and the dynamics of polymers in solution. Acta Phys. Slovaca 2015, 65, 1–64. [Google Scholar]
- Øksendal, B. Stochastic Differential Equations: An Introduction with Applications (Universitext), 6th ed.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Krafcik, A.; Babinec, P.; Frollo, I. Stokes versus Basset: Comparison of forces governing motion of small bodies with high acceleration. Eur. J. Phys. 2018, 39, 035805. [Google Scholar] [CrossRef]
- Krafcik, A.; Babinec, P.; Babincova, M.; Frollo, I. Importance of Basset history force for the description of magnetically driven motion of magnetic particles in air. Meas. Sci. Rev. 2020, 20, 50–58. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations; John Wiley & Sons, Ltd.: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Daitche, A. Advection of inertial particles in the presence of the history force: Higher order numerical schemes. J. Comput. Phys. 2013, 254, 93–106. [Google Scholar] [CrossRef] [Green Version]
- Franosch, T.; Grimm, M.; Belushkin, M.; Mor, F.; Foffi, G.; Forro, L.; Jeney, S. Resonances arising from hydrodynamic memory in Brownian motion. Nature 2011, 478, 85–88. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Chavez, I.; Taute, K.; Lukic, B.; Jeney, S.; Raizen, M.; Florin, E.L. Direct observation of the full transition from ballistic to diffusive Brownian motion in a liquid. Nat. Phys. 2011, 7, 576–580. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Lisy, V.; Tothova, J. Generalized Langevin equation and the fluctuation-dissipation theorem for particle-bath systems in a harmonic field. Results Phys. 2019, 12, 1212–1213. [Google Scholar] [CrossRef]
- Lisy, V.; Tothova, J. Brownian motion of charged particles in a bath responding to an external magnetic field. Acta Phys. Pol. A 2020, 137, 657–659. [Google Scholar] [CrossRef]
- Tothova, J.; Soltys, A.; Lisy, V. Brownian motion in a bath responding to external electric fields. J. Mol. Liq. 2020, 317, 113920. [Google Scholar] [CrossRef]
- Tothova, J.; Lisy, V. Brownian motion in a gas of charged particles under the influence of a magnetic field. Phys. A Stat. Mech. Appl. 2020, 559, 125110. [Google Scholar] [CrossRef]
- Tothova, J.; Lisy, V. Brownian motion in a bath affected by an external harmonic potential. Phys. Lett. Sect. A Gen. At. Solid. State Phys. 2021, 395, 127220. [Google Scholar] [CrossRef]




| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Finite timestep | h | ||
| Boltzmann constant | |||
| Thermodynamic temperature | T | ||
| Fluid dynamic viscosity | |||
| Fluid mass density | 1000 | ||
| Fluid kinematic viscosity | |||
| Magnetic flux density norm | |||
| Particle diameter | |||
| Particle mass density | |||
| Particle volume | |||
| Particle weight | |||
| Particle moment of inertia | |||
| Particle saturation magnetization | |||
| Particle magnetic moment | |||
| Stokes coefficient |
| No. | Torques Involved | Notation |
|---|---|---|
| (i) | inertial, magnetic, quasi-steady viscous, stochastic Brownian | SDE |
| (ii) | inertial, magnetic, arbitrary viscous, stochastic Brownian | SIDE |
| (iii) | inertial, magnetic, quasi-steady viscous, no stochastic Brownian | ODE |
| (iv) | inertial, magnetic, arbitrary viscous, no stochastic Brownian | IDE |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krafcik, A.; Babinec, P.; Strbak, O.; Frollo, I. A Theoretical Analysis of Magnetic Particle Alignment in External Magnetic Fields Affected by Viscosity and Brownian Motion. Appl. Sci. 2021, 11, 9651. https://doi.org/10.3390/app11209651
Krafcik A, Babinec P, Strbak O, Frollo I. A Theoretical Analysis of Magnetic Particle Alignment in External Magnetic Fields Affected by Viscosity and Brownian Motion. Applied Sciences. 2021; 11(20):9651. https://doi.org/10.3390/app11209651
Chicago/Turabian StyleKrafcik, Andrej, Peter Babinec, Oliver Strbak, and Ivan Frollo. 2021. "A Theoretical Analysis of Magnetic Particle Alignment in External Magnetic Fields Affected by Viscosity and Brownian Motion" Applied Sciences 11, no. 20: 9651. https://doi.org/10.3390/app11209651
APA StyleKrafcik, A., Babinec, P., Strbak, O., & Frollo, I. (2021). A Theoretical Analysis of Magnetic Particle Alignment in External Magnetic Fields Affected by Viscosity and Brownian Motion. Applied Sciences, 11(20), 9651. https://doi.org/10.3390/app11209651