Comparative Analysis of Healthy and Cam-Type Femoroacetabular Impingement (FAI) Human Hip Joints Using the Finite Element Method
Abstract
:1. Introduction
2. Femoroacetabular Impingement in Human Hip Joint
3. Materials and Methods
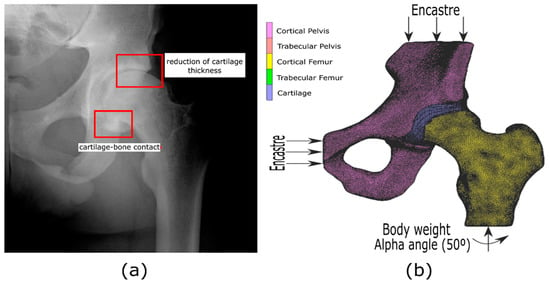
3.1. CT Acquisition, Segmentation, and Image Reconstruction
3.2. Finite Element Models Proposed
3.2.1. Mechanical Properties and Material Behavior
3.2.2. Boundary Conditions for the Proposed FE Models
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Navarro-Zarza, J.E.; Villaseñor-Ovies, P.; Vargas, A.; Canoso, J.J.; Chiapas-Gasca, K.; Hernández-Díaz, C.; Saavedra, M.Á.; Kalish, R.A. Clinical anatomy of the pelvis and hip. Reumatol. Clin. 2012, 8, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Bogunovic, L.; Nho, S.J. Femoroacetabular impingement. In Orthopaedic Knowledge Update: Sports Medicine; Wolters Kluwer Health: Philadelphia, PA, USA, 2018; Volume 5, pp. 127–140. [Google Scholar]
- Beck, M.; Kalhor, M.; Leunig, M.; Ganz, R. Hip morphology influences the pattern of damage to the acetabular cartilage. Femoroacetabular impingement as a cause of early osteoarthritis of the hip. J. Bone Jt. Surg. 2005, 87, 1012–1018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bedi, A.; Kelly, B.T. Femoroacetabular impingement. JBJS 2013, 95, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Lavigne, M.; Parvizi, J.; Beck, M.; Siebenrock, K.A.; Ganz, R.; Leunig, M. Anterior femoroacetabular impingement: Part I. Techniques of joint preserving surgery. Clin. Orthop. Relat. Res. 2004, 418, 61–66. [Google Scholar] [CrossRef]
- Konan, S.; Rayan, F.; Haddad, F.S. Is the frog lateral plain radiograph a reliable predictor of the alpha angle in femoroacetabular impingement? J. Bone Jt. Surg. 2010, 92, 47–50. [Google Scholar] [CrossRef]
- Eijer, H.; Leunig, M.; Mahomed, M.N.; Ganz, R. Cross-table lateral radiographs for screening of anterior femoral head-neck Offset in patients with femoro-acetabular impingement. HIP Int. 2001, 11, 37–41. [Google Scholar] [CrossRef]
- Ng, K.G.; Lamontagne, M.; Labrosse, M.R.; Beaulé, P.E. Hip joint stresses due to cam-type femoroacetabular impingement: A systematic review of finite element simulations. PLoS ONE 2016, 11, e0147813. [Google Scholar] [CrossRef] [PubMed]
- Chegini, S.; Beck, M.; Ferguson, S.J. The effects of impingement and dysplasia on stress distributions in the hip joint during sitting and walking: A finite element analysis. J. Orthop. Res. 2009, 27, 195–201. [Google Scholar] [CrossRef]
- Arbabi, E.; Chegini, S.; Boulic, R.; Tannast, M.; Ferguson, S.J.; Thalmann, D. Penetration depth method—Novel real-time strategy for evaluating femoroacetabular impingement. J. Orthop. Res. 2010, 28, 880–886. [Google Scholar] [CrossRef]
- Ng, K.G.; Rouhi, G.; Lamontagne, M.; Beaulé, P.E. Finite element analysis examining the effects of cam FAI on hip joint mechanical loading using subject-specific geometries during standing and maximum squat. HSS J. 2012, 8, 206–212. [Google Scholar] [CrossRef] [Green Version]
- Jorge, J.P.; Simões, F.M.F.; Pires, E.B.; Rego, P.A.; Tavares, D.G.; Lopes, D.S.; Gaspar, A. Finite element simulations of a hip joint with femoroacetabular impingement. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 1275–1284. [Google Scholar] [CrossRef] [PubMed]
- Hellwig, F.L.; Tong, J.; Hussell, J.G. Hip joint degeneration due to cam impingement: A finite element analysis. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 41–48. [Google Scholar] [CrossRef] [PubMed]
- Roels, P.; Agricola, R.; Oei, E.H.; Weinans, H.; Campoli, G.; Zadpoor, A. Mechanical factors explain development of cam-type deformity. Osteoarthr. Cartil. 2014, 22, 2074–2082. [Google Scholar] [CrossRef] [Green Version]
- Ganz, R.; Parvizi, J.; Beck, M.; Leunig, M.; Nötzli, H.; Siebenrock, K.A. Femoroacetabular impingement: A cause for osteoarthritis of the hip. Clin. Orthop. Relat. Res. 2003, 417, 112–120. [Google Scholar]
- Beck, M.; Leunig, M.; Parvizi, J.; Boutier, V.; Wyss, D.; Ganz, R. Anterior femoroacetabular impingement: Part II. Midterm results of surgical treatment. Clin. Orthop. Relat. Res. 2004, 418, 67–73. [Google Scholar] [CrossRef]
- Kim, K.C.; Hwang, D.S.; Lee, C.H.; Kwon, S.T. Influence of femoroacetabular impingement on results of hip arthroscopy in patients with early osteoarthritis. Clin. Orthop. Relat. Res. 2007, 456, 128–132. [Google Scholar] [CrossRef]
- Tannast, M.; Siebenrock, K.A.; Anderson, S.E. Femoroacetabular impingement: Radiographic diagnosis—What the radiologist should know. AJR Am. J. Roentgenol. 2007, 188, 1540–1552. [Google Scholar] [CrossRef] [Green Version]
- Ito, K.; Minka-II, M.A.; Leunig, M.; Werlen, S.; Ganz, R. Femoroacetabular impingement and the cam-effect: A MRI-based quantitative anatomical study of the femoral head-neck offset. J. Bone Jt. Surg. 2001, 83, 171–176. [Google Scholar] [CrossRef]
- Siebenrock, K.A.; Wahab, K.A.; Werlen, S.; Kalhor, M.; Leunig, M.; Ganz, R. Abnormal extension of the femoral head epiphysis as a cause of cam impingement. Clin. Orthop. Relat. Res. 2004, 418, 54–60. [Google Scholar] [CrossRef]
- Agricola, R.; Heijboer, M.P.; Ginai, A.Z.; Roels, P.; Zadpoor, A.A.; Verhaar, J.A.; Weinans, H.; Waarsing, J.H. A cam deformity is gradually acquired during skeletal maturation in adolescent and young male soccer players: A prospective study with minimum 2-year follow-up. Am. J. Sports Med. 2014, 42, 798–806. [Google Scholar] [CrossRef]
- Philippon, M.; Schenker, M.; Briggs, K.; Kuppersmith, D. Femoroacetabular impingement in 45 professional athletes: Associated pathologies and return to sport following arthroscopic decompression. Knee Surg. Sports Traumatol. Arthrosc. 2007, 15, 908–914. [Google Scholar] [CrossRef] [Green Version]
- Laude, F.; Boyer, T.; Nogier, A. Anterior femoroacetabular impingement. Jt. Bone Spine 2007, 74, 127–132. [Google Scholar] [CrossRef]
- Myers, S.R.; Eijer, H.; Ganz, R. Anterior femoroacetabular impingement after periacetabular osteotomy. Clin. Orthop. Relat. Res. 1999, 363, 93–99. [Google Scholar] [CrossRef]
- Amanatullah, D.F.; Antkowiak, T.; Pillay, K.; Patel, J.; Refaat, M.; Toupadakis, C.A.; Jamali, A.A. Femoroacetabular impingement: Current concepts in diagnosis and treatment. Orthopedics 2015, 38, 185–199. [Google Scholar] [CrossRef] [PubMed]
- Nötzli, H.P.; Wyss, T.F.; Stoecklin, C.H.; Schmid, M.R.; Treiber, K.; Hodler, J. The contour of the femoral head-neck junction as a predictor for the risk of anterior impingement. J. Bone Jt. Surg. 2002, 84, 556–560. [Google Scholar] [CrossRef]
- Kapron, A.L.; Anderson, A.E.; Aoki, S.K.; Phillips, L.G.; Petron, D.J.; Toth, R.; Peters, C.L. Radiographic prevalence of femoroacetabular impingement in collegiate football players: AAOS Exhibit Selection. JBJS 2011, 93, e111. [Google Scholar] [CrossRef]
- Heijboer, M.P.; Bierma-Zeinstra, S.M.; Verhaar, J.A.; Weinans, H.; Waarsing, J.H. Cam impingement causes osteoarthritis of the hip: A nationwide prospective cohort study (CHECK). Ann. Rheum. Dis. 2013, 72, 918–923. [Google Scholar]
- Lamontagne, M.; Brisson, N.; Kennedy, M.J.; Beaulé, P.E. Preoperative and postoperative lower-extremity joint and pelvic kinematics during maximal squatting of patients with cam femoro-acetabular impingement. JBJS 2011, 93 (Suppl. 2), 40–45. [Google Scholar] [CrossRef]
- Lamontagne, M.; Kennedy, M.J.; Beaulé, P.E. The effect of cam FAI on hip and pelvic motion during maximum squat. Clin. Orthop. Relat. Res. 2009, 467, 645–650. [Google Scholar] [CrossRef] [Green Version]
- Ng, K.G.; Lamontagne, M.; Adamczyk, A.P.; Rahkra, K.S.; Beaulé, P.E. Patient-specific anatomical and functional parameters provide new insights into the pathomechanism of cam FAI. Clin. Orthop. Relat. Res. 2015, 473, 1289–1296. [Google Scholar] [CrossRef] [Green Version]
- Speirs, A.D.; Beaulé, P.E.; Rakhra, K.S.; Schweitzer, M.E.; Frei, H. Increased acetabular subchondral bone density is associated with cam-type femoroacetabular impingement. Osteoarthr. Cartil. 2013, 21, 551–558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jaberi, F.M.; Parvizi, J. Hip pain in young adults: Femoroacetabular impingement. J. Arthroplast. 2007, 22, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Standaert, C.J.; Herring, S.A. Expert opinion and controversies in musculoskeletal and sports medicine: Stingers. Arch. Phys. Med. Rehabil. 2009, 90, 402–406. [Google Scholar] [CrossRef]
- Ergen, F.B.; Vudalı, S.; Şanverdi, E.; Dolgun, A.; Aydıngöz, Ü. CT assessment of asymptomatic hip joints for the background of femoroacetabular impingement morphology. Diagn. Interv. Radiol. 2014, 20, 271. [Google Scholar] [CrossRef] [PubMed]
- Jung, K.; Restrepo, C.; Hellman, M.; AbdelSalam, H.; Morrison, W.; Parvizi, J. The prevalence of cam-type femoroacetabular deformity in asymptomatic adults. J. Bone Jt. Surg. 2011, 93, 1303–1307. [Google Scholar] [CrossRef] [Green Version]
- Camacho-Alvarez, D.; Mardones-Peterman, R. Femoroacetabular impingement: Association between the overcoverage and acetabular cartilage delamination areas. Rev. Esp. Cir. Ortop. Traumatol. Engl. Ed. 2013, 57, 111–116. [Google Scholar] [CrossRef]
- Souza, B.G.S.; Cardoso, R.M.; Loque, R.S.; Monte, L.F.R.; Sabino, J.P.; de Oliveira, V.M. Mixed-type femoroacetabular impingement associated with subspine impingement: Recognizing the trifocal femoropelvic impingement. Rev. Bras. Ortop. Engl. Ed. 2018, 53, 389–394. [Google Scholar] [CrossRef]
- İnan, U.; Harmanşa, S.; Ömeroğlu, H. Treatment of mixed type femoroacetabular impingement using safe surgical hip dislocation in adults. Jt. Dis. Relat. Surg. 2016, 27, 160–166. [Google Scholar] [CrossRef]
- Cavas, F.; Piñero, D.; Velázquez, J.S.; Mira, J.; Alió, J.L. Relationship between corneal morphogeometrical properties and biomechanical parameters derived from dynamic bidirectional air applanation measurement procedure in keratoconus. Diagnostics 2020, 10, 640. [Google Scholar] [CrossRef]
- Velázquez, J.S.; Cavas, F.; Piñero, D.P.; Cañavate, F.J.; Del Barrio, J.A.; Alio, J.L. Morphogeometric analysis for characterization of keratoconus considering the spatial localization and projection of apex and minimum corneal thickness point. J. Adv. Res. 2020, 24, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Alifa, R.; Piñero, D.; Velázquez, J.; Alió del Barrio, J.L.; Cavas, F.; Alió, J.L. Changes in the 3D corneal structure and morphogeometric properties in keratoconus after corneal collagen crosslinking. Diagnostics 2020, 10, 397. [Google Scholar] [CrossRef]
- Toprak, I.; Cavas, F.; Vega, A.; Velázquez, J.S.; Alio del Barrio, J.L.; Alio, J.L. Evidence of a down syndrome keratopathy: A three-dimensional (3-D) morphogeometric and volumetric analysis. J. Pers. Med. 2021, 11, 82. [Google Scholar] [CrossRef]
- Toprak, I.; Cavas, F.; Velázquez, J.S.; Del Barrio, J.L.A.; Alió, J.L. Three-dimensional morphogeometric and volumetric characterization of cornea in pediatric patients with early keratoconus. Am. J. Ophthalmol. 2021, 222, 102–111. [Google Scholar] [CrossRef]
- Goerne, H.; Rajiah, P. Computed tomography. In Right Heart Pathology: From Mechanism to Management; Springer International Publishing: Cham, Switzerland, 2018; pp. 601–612. [Google Scholar]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.-C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M.; et al. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Autodesk Meshmixer. Available online: http://www.meshmixer.com/ (accessed on 7 May 2019).
- MSC Mentat Marc [Software]; MSC Software Corporation: Newport Beach, CA, USA, 2014.
- Rothenfluh, E.; Zingg, P.; Dora, C.; Snedeker, J.G.; Favre, P. Influence of resection geometry on fracture risk in the treatment of femoroacetabular impingement: A finite element study. Am. J. Sports Med. 2021, 40, 2002–2008. [Google Scholar] [CrossRef] [PubMed]
- Liechti, E.F.; Ferguson, S.J.; Tannast, M. Protrusio acetabuli: Joint loading with severe pincer impingement and its theoretical implications for surgical therapy. J. Orthop. Res. 2015, 33, 106–113. [Google Scholar] [CrossRef] [Green Version]
- Ng, K.G.; Mantovani, G.; Lamontagne, M.; Labrosse, M.R.; Beaulé, P.E. Cam FAI and smaller neck angles increase subchondral bone stresses during squatting: A finite element analysis. Clin. Orthop. Relat. Res. 2019, 477, 1053. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Rasgado, T.; Jimenez-Cruz, D.; Bailey, C.G.; Mandal, P.; Board, T. Changes in the stress in the femoral head neck junction after osteochondroplasty for hip impingement: A finite element study. J. Orthop. Res. 2012, 30, 1999–2006. [Google Scholar] [CrossRef] [PubMed]









| Element Size [mm] | Comp. Cost Healthy [Min.] | von Mises Healthy [MPa] | Comp. Cost Cam-Type [Min.] | von Mises Cam-Type [MPa] |
|---|---|---|---|---|
| 1.6 | 1057 | 0.52 | 1177 | 1.09 |
| 1.2 | 1428 | 0.77 | 1492 | 1.83 |
| 1.0 | 1575 | 0.89 | 1662 | 2.14 |
| 0.65 | 1718 | 0.96 | 1987 | 2.27 |
| 0.32 | 2184 | 0.98 | 2319 | 2.28 |
| Healthy Hip Joint | Cam-Type Hip Joint | |||
|---|---|---|---|---|
| Elements | Nodes | Elements | Nodes | |
| Pelvis | 285,785 | 66,477 | 285,649 | 66,474 |
| Cartilage | 46,285 | 13,285 | 45,849 | 13,159 |
| Femur | 186,265 | 42,121 | 186,198 | 42,105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lostado Lorza, R.; Somovilla Gomez, F.; Corral Bobadilla, M.; Íñiguez Macedo, S.; Rodríguez San Miguel, A.; Fernández Martínez, E.; Rubio Sampedro, M.; Pérez Sala, Á.; Cristóbal, R.P.; Larráyoz, I.M. Comparative Analysis of Healthy and Cam-Type Femoroacetabular Impingement (FAI) Human Hip Joints Using the Finite Element Method. Appl. Sci. 2021, 11, 11101. https://doi.org/10.3390/app112311101
Lostado Lorza R, Somovilla Gomez F, Corral Bobadilla M, Íñiguez Macedo S, Rodríguez San Miguel A, Fernández Martínez E, Rubio Sampedro M, Pérez Sala Á, Cristóbal RP, Larráyoz IM. Comparative Analysis of Healthy and Cam-Type Femoroacetabular Impingement (FAI) Human Hip Joints Using the Finite Element Method. Applied Sciences. 2021; 11(23):11101. https://doi.org/10.3390/app112311101
Chicago/Turabian StyleLostado Lorza, Rubén, Fátima Somovilla Gomez, Marina Corral Bobadilla, Saúl Íñiguez Macedo, Asier Rodríguez San Miguel, Enrique Fernández Martínez, Manuel Rubio Sampedro, Álvaro Pérez Sala, Rafael Peláez Cristóbal, and Ignacio M. Larráyoz. 2021. "Comparative Analysis of Healthy and Cam-Type Femoroacetabular Impingement (FAI) Human Hip Joints Using the Finite Element Method" Applied Sciences 11, no. 23: 11101. https://doi.org/10.3390/app112311101
APA StyleLostado Lorza, R., Somovilla Gomez, F., Corral Bobadilla, M., Íñiguez Macedo, S., Rodríguez San Miguel, A., Fernández Martínez, E., Rubio Sampedro, M., Pérez Sala, Á., Cristóbal, R. P., & Larráyoz, I. M. (2021). Comparative Analysis of Healthy and Cam-Type Femoroacetabular Impingement (FAI) Human Hip Joints Using the Finite Element Method. Applied Sciences, 11(23), 11101. https://doi.org/10.3390/app112311101