Author Contributions
Conceptualization, D.G. and C.D.; data curation, D.G.; formal analysis, D.G. and R.I.; funding acquisition, C.D.; investigation, D.G., C.D. and R.I.; methodology, D.G. and A.E.H.; project administration, C.D.; resources, D.G., C.D. and A.E.H.; supervision, C.D. and A.E.H.; validation, D.G., C.D., R.I. and A.E.H.; visualization, D.G.; writing—original draft, D.G. and C.D.; writing—review and editing, D.G., C.D. and A.E.H. All authors have read and agreed to the published version of the manuscript.
Figure 1.
(a) Density map in a 16 × 18 cm block of Ciply Chalk obtained by CT scan. (b) SEM micrograph showing the heterogeneous microstructure in Ciply Chalk. (c) Close view of a brain-like nodule made of fluorapatite.
Figure 1.
(a) Density map in a 16 × 18 cm block of Ciply Chalk obtained by CT scan. (b) SEM micrograph showing the heterogeneous microstructure in Ciply Chalk. (c) Close view of a brain-like nodule made of fluorapatite.
Figure 2.
(a) Device used for conducting Brazilian tests for the determination of the tensile strength. (b) Sketch of the setup used for conducting standard triaxial tests and injection tests in a pressure vessel.
Figure 2.
(a) Device used for conducting Brazilian tests for the determination of the tensile strength. (b) Sketch of the setup used for conducting standard triaxial tests and injection tests in a pressure vessel.
Figure 3.
View of the open pressure vessel and sketch explaining the protocol used for the injection tests. ΔP is the fluid pressure difference between the bottom and top of the sample.
Figure 3.
View of the open pressure vessel and sketch explaining the protocol used for the injection tests. ΔP is the fluid pressure difference between the bottom and top of the sample.
Figure 4.
The new device developed at GEC laboratory for measuring the mode I fracture toughness. The sample geometry is given on the right and the requirements for the different parameters are summarized in the table.
Figure 4.
The new device developed at GEC laboratory for measuring the mode I fracture toughness. The sample geometry is given on the right and the requirements for the different parameters are summarized in the table.
Figure 5.
Cylindrical rock plugs of Ciply Chalk (bottom left) and Obourg Chalk (bottom right), and pure single calcite (top) used for surface characterization. The scale is given by the ruler in mm.
Figure 5.
Cylindrical rock plugs of Ciply Chalk (bottom left) and Obourg Chalk (bottom right), and pure single calcite (top) used for surface characterization. The scale is given by the ruler in mm.
Figure 6.
(
a) Bruker™ “dimension icon” Atomic Force Microscope [
15] with the Scanasyst-Air
® probe [
16] on the right top corner. (
b) Typical cycle of force vs. time in the Peak Force Tapping mode.
Figure 6.
(
a) Bruker™ “dimension icon” Atomic Force Microscope [
15] with the Scanasyst-Air
® probe [
16] on the right top corner. (
b) Typical cycle of force vs. time in the Peak Force Tapping mode.
Figure 7.
(a) Drop shape analysis profile (DSA-P) device from Kruss™. (b) Example of picture used to measure the contact angle on a surface through a dedicated software.
Figure 7.
(a) Drop shape analysis profile (DSA-P) device from Kruss™. (b) Example of picture used to measure the contact angle on a surface through a dedicated software.
Figure 8.
UCS values for the Obourg chalk vs. porosity for 100 samples with different fluid content.
Figure 8.
UCS values for the Obourg chalk vs. porosity for 100 samples with different fluid content.
Figure 9.
Triaxial tests at 1.5 MPa effective confining pressure for Obourg and Ciply chalks with different fluids saturating the pore space. The y-axis scale is the same for both plots.
Figure 9.
Triaxial tests at 1.5 MPa effective confining pressure for Obourg and Ciply chalks with different fluids saturating the pore space. The y-axis scale is the same for both plots.
Figure 10.
Yielding envelopes obtained from the yield stresses for both chalks saturated with different fluids. Solids symbols are for conventional triaxial tests, open symbols are for data obtained using a multistage loading approach on a single sample. The y-axis scale is the same for both plots.
Figure 10.
Yielding envelopes obtained from the yield stresses for both chalks saturated with different fluids. Solids symbols are for conventional triaxial tests, open symbols are for data obtained using a multistage loading approach on a single sample. The y-axis scale is the same for both plots.
Figure 11.
Mohr circles obtained from triaxial tests on dry (in red) and water-saturated (in blue) Obourg Chalk samples. The Coulomb failure lines were derived by a least-squares fitting scheme using the points with error bars on the plot.
Figure 11.
Mohr circles obtained from triaxial tests on dry (in red) and water-saturated (in blue) Obourg Chalk samples. The Coulomb failure lines were derived by a least-squares fitting scheme using the points with error bars on the plot.
Figure 12.
(a) Injected water volume normalized to pore volume vs. applied differential stress normalized to the strength of the dry rock at fixed confining pressure (1.5 MPa). (b) Samples after failure induced by water injection at constant stress level.
Figure 12.
(a) Injected water volume normalized to pore volume vs. applied differential stress normalized to the strength of the dry rock at fixed confining pressure (1.5 MPa). (b) Samples after failure induced by water injection at constant stress level.
Figure 13.
Results for acoustic monitoring of the P wave velocity (top) and amplitude (bottom) during injection tests in Obourg (left) and Ciply (right) Chalks at 1.5 MPa confining pressure. The different colors correspond to measurements at different heights in the bottom (red), middle (green), and top (blue) planes. The velocity and amplitude scale are the same for the Obourg and Ciply Chalks plots.
Figure 13.
Results for acoustic monitoring of the P wave velocity (top) and amplitude (bottom) during injection tests in Obourg (left) and Ciply (right) Chalks at 1.5 MPa confining pressure. The different colors correspond to measurements at different heights in the bottom (red), middle (green), and top (blue) planes. The velocity and amplitude scale are the same for the Obourg and Ciply Chalks plots.
Figure 14.
(a) Application of the Owens–Wendt method to get the two components of surface energy from the linear regression. (b) Contact angle measurements vs. ionic strength for NaCl and MgCl2 brines in contact with a single calcite crystal.
Figure 14.
(a) Application of the Owens–Wendt method to get the two components of surface energy from the linear regression. (b) Contact angle measurements vs. ionic strength for NaCl and MgCl2 brines in contact with a single calcite crystal.
Figure 15.
(a) Example of 3D topography on a 10 × 10 μm surface obtained on Obourg chalk. (b) Example of adhesion force map on a 10 × 10 μm surface for Obourg chalk.
Figure 15.
(a) Example of 3D topography on a 10 × 10 μm surface obtained on Obourg chalk. (b) Example of adhesion force map on a 10 × 10 μm surface for Obourg chalk.
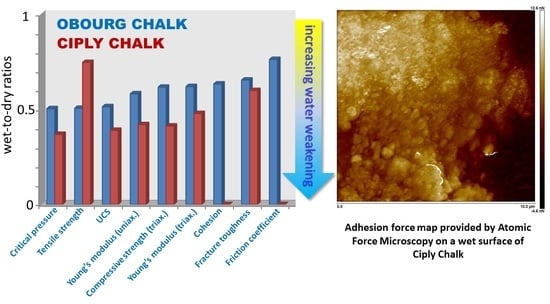
Figure 16.
Bar chart with the wet-to-dry ratios in increasing order for each chalk.
Figure 16.
Bar chart with the wet-to-dry ratios in increasing order for each chalk.
Figure 17.
Schematic drawing of the repulsive effect (a) in a water-saturated chalk, (b) in a brine-saturated chalk. For the sake of simplicity, the relative size of the water molecule with respect to Mg2+ and Cl- ions is not respected.
Figure 17.
Schematic drawing of the repulsive effect (a) in a water-saturated chalk, (b) in a brine-saturated chalk. For the sake of simplicity, the relative size of the water molecule with respect to Mg2+ and Cl- ions is not respected.
Table 1.
Composition and petrophysical properties of the selected rocks.
Table 1.
Composition and petrophysical properties of the selected rocks.
| | Obourg Chalk | Ciply Chalk |
|---|
| mineralogical composition | calcite | calcite, fluorapatite |
| grain density (kg/m3) | 2720 | 2730 |
| bulk density (kg/m3) | 1550 | 1680 |
| average porosity | 0.43 | 0.39 |
| average permeability (m2) | 6.4 · 10−16 | 4.0 · 10−14 |
Table 2.
Dispersive and polar components of the free surface energy for the 5 fluids used in our experiments. The total free energy is the sum of both components. DW = distilled water/DIO = Diiodomethane/Form = Formamide/DMSO = Dimethyl Sulfoxide/Glyc = Glycerol.
Table 2.
Dispersive and polar components of the free surface energy for the 5 fluids used in our experiments. The total free energy is the sum of both components. DW = distilled water/DIO = Diiodomethane/Form = Formamide/DMSO = Dimethyl Sulfoxide/Glyc = Glycerol.
| Free Surface Energy (mJ/m2) | DW | DIO | Form | DMSO | Glyc |
|---|
| Dispersive component γ(D) | 21.8 | 48.5 | 39.5 | 36.0 | 34.0 |
| Polar component γ(P) | 51.0 | 2.3 | 18.7 | 8.0 | 30.0 |
| Total free energy | 72.8 | 50.8 | 58.2 | 44.0 | 64.0 |
Table 3.
Tensile strength values for both chalks for dry and water-saturated samples.
Table 3.
Tensile strength values for both chalks for dry and water-saturated samples.
| | Obourg Chalk | Ciply Chalk |
|---|
| Pore Fluid | Number of Samples | TENSILE Strength (MPa) | Standard Deviation (MPa) | Number of Samples | Tensile Strength (MPa) | Standard Deviation (MPa) |
|---|
| Air (dry) | 4 | −0.87 | 0.14 | 1 | −0.75 | - |
| Distilled water | 2 | −0.44 | 0.07 | 2 | −0.56 | 0.15 |
Table 4.
Compressive strengths and elastic moduli for both chalks tested under dry and water-saturated conditions at 1.5 MPa effective confining pressure. Two Obourg chalk samples were tested in order to check the reproducibility of the experiments. Additional experiments were conducted on Obourg Chalk with two different brines saturating the pores.
Table 4.
Compressive strengths and elastic moduli for both chalks tested under dry and water-saturated conditions at 1.5 MPa effective confining pressure. Two Obourg chalk samples were tested in order to check the reproducibility of the experiments. Additional experiments were conducted on Obourg Chalk with two different brines saturating the pores.
| | Obourg Chalk | Ciply Chalk |
|---|
| Pore Fluid | Compressive Strength (MPa) | Young’s Modulus (GPa) | Compressive Strength (MPa) | Young’s Modulus (GPa) |
|---|
| Air (dry sample) | 11.1 | 5.0 | 9.7 | 2.3 |
| 10.3 | 4.9 |
| Deionized water | 6.5 | 3.1 | 4 | 1.1 |
| 6.7 | 3.1 |
| Brine 35 g/L NaCl | 6.7 | 3.2 | X | X |
| Brine 35 g/L MgCl2 | 8.8 | 3.8 | X | X |
Table 5.
Compilation of fracture toughness measurements for Obourg and Ciply Chalk samples saturated with different pore fluids.
Table 5.
Compilation of fracture toughness measurements for Obourg and Ciply Chalk samples saturated with different pore fluids.
| | Obourg Chalk | Ciply Chalk |
|---|
| Pore Fluid | Number of Samples | KIC (MPa·m1/2) | Standard Deviation (MPa·m1/2) | Number of Samples | KIC (MPa·m1/2) | Standard Deviation (MPa·m1/2) |
|---|
| Air (dry) | 7 | 0.0778 | 0.0086 | 3 | 0.0479 | 0.0142 |
| Distilled water | 6 | 0.0509 | 0.0068 | 3 | 0.0287 | 0.0042 |
| NaCl brine | 3 | 0.0379 | 0.0015 | – | – | – |
| MgCl2 brine | 3 | 0.0425 | 0.0141 | – | – | – |
| CaCl2 brine | 3 | 0.0458 | 0.0077 | – | – | – |
Table 6.
Average advancing contact angle of different model fluids on the different studied surfaces (see caption of
Table 2 for fluid nomenclature) and surface roughness measured by AFM and laser confocal microscopy. For calcite crystal only three fluids were tested.
Table 6.
Average advancing contact angle of different model fluids on the different studied surfaces (see caption of
Table 2 for fluid nomenclature) and surface roughness measured by AFM and laser confocal microscopy. For calcite crystal only three fluids were tested.
| | Average Advancing Contact Angle (°) | Roughness Ra (nm) |
|---|
| DW | DIO | Form | DMSO | Glyc | AFM | Confocal |
|---|
| Obourg + Resin | 89.4 ± 4.7 | 74.2 ± 4.9 | 77.6 ± 3.5 | 53.5 ± 4.3 | 77.8 ± 3.6 | 72.5 ± 19.5 | 893 ± 40 |
| Ciply + Resin | 86.0 ± 4.3 | 72.4 ± 4.0 | 70.5 ± 5.3 | 56.3 ± 3.0 | 75.8 ± 4.1 | 58.8 ± 21.9 | 511 ± 480 |
| Calcite crystal | 77.8 ± 4.9 | 71.3 ± 3.5 | 73.8 ± 7.1 | – | – | – | 2766 ± 919 |
| Resin | 80.7 ± 4.2 | 75.2 ± 5.0 | 69.5 ± 4.4 | 55.1 ± 4.8 | 70.3 ± 4.8 | – | – |
Table 7.
Compilation of experimental results for the mechanical tests conducted on the dry and water-saturated chalks. The wet-to-dry ratios WDR(Λ) are given for the corresponding parameters Λ.
Table 7.
Compilation of experimental results for the mechanical tests conducted on the dry and water-saturated chalks. The wet-to-dry ratios WDR(Λ) are given for the corresponding parameters Λ.
| | | Obourg Chalk | Ciply Chalk |
|---|
| Testing Method | Properties | Dry rock | Water Saturated Rock | Wet-to-Dry Ratio | Dry Rock | Water Saturated Rock | Wet-to-Dry Ratio |
|---|
| Uniaxial compression | UCS (MPa) | 7.0 | 3.6 | 0.51 | 4.4 | 1.7 | 0.39 |
| Young’s Modulus (GPa) | 5.5 | 3.2 | 0.58 | 1.2 | 0.5 | 0.42 |
| Brazilian test | Tensile strength (MPa) | −0.87 | −0.44 | 0.51 | −0.75 | −0.56 | 0.75 |
| Triaxial compression @1.5 MPa confining pressure | Compressive strength (MPa) | 10.7 | 6.6 | 0.62 | 9.7 | 4.0 | 0.41 |
| Young’s Modulus (GPa) | 5.0 | 3.1 | 0.62 | 2.3 | 1.1 | 0.48 |
| Isotropic compression | Critical pressure (MPa) | 14.1 | 7.1 | 0.5 | 16.0 | 5.9 | 0.37 |
| Triaxial tests | Internal friction coefficient (-) | 0.59 | 0.45 | 0.76 | X | X | X |
| Cohesion (MPa) | 2.13 | 1.35 | 0.63 | X | X | X |
| Semi-circular bending test | Fracture toughness KIC (MPa∙m1/2) | 0.0778 | 0.0509 | 0.65 | 0.0479 | 0.0287 | 0.60 |
Table 8.
Surface energy derived from the three different methods tested in this work.
Table 8.
Surface energy derived from the three different methods tested in this work.
| | Obourg Chalk | Ciply Chalk |
|---|
| Surface Energy (J/m2) | Dry Rock | Water-Saturated Rock | | Dry Rock | Water-Saturated Rock | |
|---|
| From contact angle measurements | 0.0234 | not measurable | X | 0.0253 | not measurable | X |
| From AFM | 0.0207 | 0.0165 | 0.80 | 0.0196 | 0.0141 | 0.72 |
| From KIC measurements | 0.5270 | 0.4150 | 0.79 | 1.01 | 0.84 | 0.83 |