Next Article in Journal
Impact of Construction Method and Ground Composition on Headrace Tunnel Stability in the Neelum–Jhelum Hydroelectric Project: A Case Study Review from Pakistan
Next Article in Special Issue
Topology Optimisation in Structural Steel Design for Additive Manufacturing
Previous Article in Journal
Analysis of Mixed-Mode I/II/III Fracture Toughness Based on a Three-Point Bending Sandstone Specimen with an Inclined Crack
Previous Article in Special Issue
Design for Additive Manufacturing: Tool Review and a Case Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 11
Issue 4
10.3390/app11041654
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

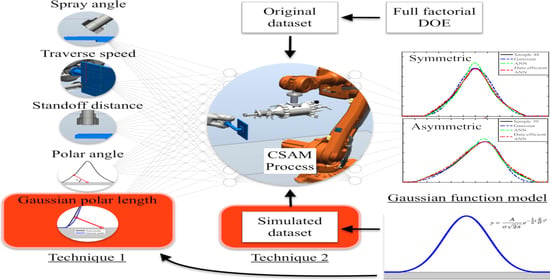
Data-Efficient Neural Network for Track Profile Modelling in Cold Spray Additive Manufacturing

by
Daiki Ikeuchi
1,2,*,†,
Alejandro Vargas-Uscategui
2,
Xiaofeng Wu
1 and
Peter C. King
2
1
School of Aerospace, Mechanical and Mechatronic Engineering, The University of Sydney, Sydney, NSW 2006, Australia
2
Commonwealth Scientific and Industrial Research Organisation Manufacturing, Private Bag 10, Clayton, VIC 3169, Australia
*
Author to whom correspondence should be addressed.
†
Now at: Department of Engineering, University of Cambridge, Cambridge, CB2 1PZ, UK.
Appl. Sci. 2021, 11(4), 1654; https://doi.org/10.3390/app11041654
Submission received: 25 January 2021 / Revised: 7 February 2021 / Accepted: 9 February 2021 / Published: 12 February 2021
(This article belongs to the Special Issue Design for Additive Manufacturing: Methods and Tools)
Browse Figures
Versions Notes

Abstract

:

Featured Application

This study presents a data-efficient modelling approach for a single-track profile in Cold Spray Additive Manufacturing using an artificial neural network. The approach presented in this study can be extended to modelling cases of other deposition-based additive manufacturing technologies with a high deposition rate, such as Wire and Arc Additive Manufacturing and Laser Cladding. The developed model can serve as a tool in simulation software by defining a realisable feature size at product design phases and predicting an as-fabricated product in these near-net-shaped manufacturing technologies. Hence, it allows designers to form a better idea of product design limitation and potential material waste after post-machining, as well as assessing and minimising economic and environmental impact with the aid of an appropriate toolpath planning algorithm.

Abstract

Cold spray is emerging as an additive manufacturing technique, particularly advantageous when high production rate and large build sizes are in demand. To further accelerate technology’s industrial maturity, the problem of geometric control must be improved, and a neural network model has emerged to predict additively manufactured geometry. However, limited data on the effect of deposition conditions on geometry growth is often problematic. Therefore, this study presents data-efficient neural network modelling of a single-track profile in cold spray additive manufacturing. Two modelling techniques harnessing prior knowledge or existing model were proposed, and both were found to be effective in achieving the data-efficient development of a neural network model. We also showed that the proposed data-efficient neural network model provided better predictive performance than the previously proposed Gaussian function model and purely data-driven neural network. The results indicate that a neural network model can outperform a widely used mathematical model with data-efficient modelling techniques and be better suited to improving geometric control in cold spray additive manufacturing.

Graphical Abstract

1. Introduction

Cold spray is a solid-state materials deposition technology that employs a supersonic gas jet to accelerate powder particles to 500–1000 m/s. Due to the particles’ kinetic energy, local metallurgical bonding and mechanical interlocking are achieved without in-flight melting. This characteristic provides unique advantages that are difficult to achieve otherwise, including deposition free of melting-induced microstructure changes, the ability to handle oxygen-sensitive materials without a protective atmosphere and a high deposition rate with a narrow nozzle diameter [1,2,3,4].
Cold spray has recently been recognised to possess great potential as an alternative additive manufacturing technology and in this context is referred to as Cold Spray Additive Manufacturing (CSAM) [5,6,7,8]. This potential is particularly important when high production rates, large build sizes and repair or building on an existing structure are in demand, e.g., in aerospace industries [8,9]. The protective atmosphere-free environment allows for the fabrication of large components that are not possible with other additive manufacturing technologies, e.g., powder bed fusion, while providing a flexible selection of oxygen-sensitive powder materials [8,10,11]. These benefits have resulted in several successful demonstrations of the technology at different levels of fabrication complexity, ranging from a simple tubular structure [12], pyramidal fin array [13], to more complex parts such as topologically optimised components [14].
However, several fundamental and practical challenges need to be addressed to fully adopt the CSAM technology in commercial applications. One of these is geometric control, which is a common problem for other high production rate additive manufacturing (HPRAM) processes, including Wire and Arc Additive Manufacturing (WAAM) [15,16] and Laser Cladding (LC) [17,18]. Poor geometric control places many limitations on applying HPRAM technologies; examples include varying geometric quality, difficulty producing complex geometries, and geometry-induced property variations [7,8,19]. Hence, geometric control must be addressed to facilitate further development and commercial integration of CSAM and other HPRAM technologies.
Given the track-by-track and layer-by-layer nature of HPRAM, a high-accuracy process model based on the shape of a characteristic processing unit (e.g., single-track profile) provides a promising solution to the problem and often forms a basis for the modelling of higher geometric processing units, such as overlapping and overlayer models [20,21]. The single-track profile modelling in HPRAM was previously attempted using two distinct approaches: mathematical and data-driven modelling.
In WAAM, the symmetric single-track bead profile has been approximated using various basic mathematical function models ranging from parabolic, cosine and arcs [22,23]. These mathematical function models are often combined with another regression model to provide predictive capabilities. For example, Suryakumar et al. developed a quadratic regression model based on experimental data, computing the coefficients of the parabolic function model to describe a single-track bead profile [22]. In CSAM, a mathematical Gaussian function model is often chosen due to the mass distribution of jetted powder being assumed to be of Gaussian function profile [24,25]. Some other studies have utilised different mathematical function models, such as triangular [26,27] and trapezoidal [28]. Due to the complex processes underlying each HPRAM, there is no agreement on the choice of a single mathematical function model with simplifying assumptions, and the suitable model often depends on process conditions and their combination [23], leading to limited prediction accuracy over a wide range of process conditions using only a single mathematical functional model.
Data-driven modelling has emerged as an alternative approach due to its excellent nonlinear mapping capability and increased accessibility of available software options [18,29]. Xiong et al. developed an Artificial Neural Network (ANN) model to predict the height and width of a single-track bead profile in WAAM [30]. The results were compared with those of a quadratic regression model and showed that the ANN model outperformed in the prediction of key geometric features. However, data-driven modelling has previously been limited to only predicting the height and width in HPRAM, and unlike the mathematical modelling approach, it has not been adopted to describe an entire track profile. Thus, there has been no exploration of the technique beyond symmetric single-track profiles or predicting details in track profiles. Our previous study attempted to address this issue in CSAM, focusing on the ANN modelling of a single-track profile with high morphology at normal and off-normal spray angles [31]. Our results demonstrated the potential of a data-driven modelling approach for better prediction accuracy than a mathematical counterpart, i.e., the Gaussian function model.
However, the limitation of a data-driven modelling approach was also observed in our previous study [31], namely, the necessity of a large amount of process training data to achieve a high prediction accuracy, which has also been identified recently in relevant manufacturing studies [32,33]. This data scarcity issue is associated with high experimental costs and the lack of an automated measurement system in HPRAM. Liu et al. applied a grey modelling technique for the first time in a thermal spray process in an attempt to overcome the issue, harnessing both mathematical (or white box) and data-driven (or black-box) modelling approaches [32]. Despite the reasonable prediction accuracy achieved in this study, the authors concluded that more complex and nonlinear phenomena existed and suggested further exploration of data-efficient modelling approaches to improve prediction accuracy.
Therefore, this study focuses on the prediction of a single-track profile in CSAM, at both normal and off-normal spray angles, using a data-efficient ANN (DANN) approach to demonstrate that data-driven modelling can achieve better prediction accuracy than its mathematical counterpart that has already been adopted in CSAM. Inspired by the study by Liu et al. [32], we leverage a mathematical function model as domain knowledge or the existing model at hand into the development of a DANN model. Specifically, a Gaussian function model, the model adopted elsewhere in CSAM studies, is selected with its coefficients computed by a quadratic regression model as applied in [22]. The significance of this study is four-fold: (1) the application of a data-driven modelling approach with a data-efficient focus in the prediction of a single-track profile in CSAM; (2) the comparative study among purely mathematical function, purely data-driven and data-efficient data-driven modelling approaches, in the context of HPRAM; (3) the demonstration that data-driven modelling can outperform more widely used mathematical modelling with appropriate data-efficient techniques in HPRAM; and (4) that existing models at hand can contribute to the development of a new data-driven model with better prediction accuracy without further experimentation.

2. Materials and Methods

An ANN is a feed-forward network model for supervised machine learning that performs the mapping of an input–output relationship based on appropriate training data. The development of an ANN with sufficient prediction accuracy depends on several pre-processing factors, including selecting appropriate input variables, quality of data and network architecture [34,35]. In this study, three experimental process variables were selected as inputs to an ANN model: spray angle, traverse speed and standoff distance, together with other input variables subsequently introduced in Section 2.2. This selection was made based on previous studies, demonstrating their influence on the geometry of a track profile in CSAM [24,36] and precise control with a robotic system [37].
A full factorial method was employed to define the experimental process variables’ values in the ANN training dataset and design the set of experimental conditions. This approach was selected due to the nonlinear nature of CSAM and the affordable number of the process variables in this study. Here, three levels were considered for traverse speed and standoff distance, while four levels were adopted to effectively capture the effects of spray angle on track profiles in CSAM. The values of these process variables at each level are listed in Table 1. The minimum and maximum level values of each process variable corresponded to their operating limits to ensure the sufficient quality of track profiles. The intermediate level values were then equally placed between the values at each extreme level to maximise possible interactions between the process variables [38]. The resulting experimental design matrix in the full factorial method required 36 experimental single-track profiles for the proposed ANN modelling as a training dataset. The detailed experimental conditions of each single-track profile are summarised in Tables S1 and S2 in the Supplementary Materials.

2.1. Sample Preparation

All experimental single-track profiles were prepared using a commercial Impact Innovations (Haun, Germany) 5/11 cold spray gun guided by an ABB (Zurich, Switzerland) 4600 robot with 6 degrees of freedom, as can be seen in [39]. The gun was equipped with a long pre-chamber and an OUT1 tungsten carbide de Laval nozzle with a 6.2 mm exit diameter from Impact Innovations. The powder feedstock in this study was commercial purity grade −2 titanium from AP&C (Boisbriand, Canada) which was prepared by gas atomisation and distributed within the size of 15 to 45 µm (i.e., D10 = 19 µm, D50 = 34 µm and D90 = 45 µm). The working gas was Nitrogen, preheated to 600 °C at a pressure of 5 MPa, accelerating the powder particles injected into the nozzle upstream at a feed rate of 1.9 kg/h. All spray variables and conditions were held constant during all experiments, except those listed in Table 1. A strip of commercial purity grade −2 titanium was used as a substrate with a dimension of 6 × 30 × 200 mm, having its surface processed with a milling machine from Avemax Machinery (Taichung City, Taiwan) and subsequently ground with a P120-SiC emery paper from LECO (Moenchengladbach, Germany). This surface processing was followed by cleaning with ethanol before the experiments. The fabrication of experimental single-track profiles was randomised to ensure statistically unbiased results with minimal effects of potential extraneous factors [40]. RobotStudio® software version 6.08 (ABB Robotics, Zurich, Switzerland) was used to confirm that there was sufficient distance beyond the substrate’s edge to ensure that the robot’s trajectory and traverse speed were stabilised before fabricating the profiles.
The geometry of each single-track profile was measured at five randomly selected locations using a LEXT OLS4000 confocal laser scanning microscope (Tokyo, Japan) and scanControl 2950–100 laser scanner from Micro-Epsilon (Ortenburg, Germany) with a z-axis measuring precision of at least 12 µm. These measurements were processed with the in-built filtering methods: flat Surface filtering in LEXT OLS4000 and average filtering with a filter size of 7 in scanControl Configuration Tool version 6.0. Additional filtering was applied with a local regression method using weighted linear least square and second-order polynomial model in MATLAB version R2018a. The five filtered track profiles were averaged to form each sample profile, as depicted in Figures S1–S3 in the Supplementary Materials, which was then considered for all modelling approaches in this study.

2.2. Data-Efficent Artificial Neural Network Model Design and Training

To demonstrate the effectiveness of leveraging a previous modelling attempt or existing model, a mathematical Gaussian function model, previously proposed in [24] and expressed in Equation 1, was selected and built with its free coefficients, A and σ, being predicted using a quadratic regression model as applied in [22].
y = A σ 2 π e − 1 2 x σ 2 ,
This selection was due to the mathematical model framework being capable of predicting an asymmetric single-track profile at off-normal angles and being often used in cold spray and CSAM [24,25,36]. For preparing the training dataset of outputs for the quadratic regression model, appropriate free coefficients were found through a Gaussian function equation curve fitting to each single-track profile shown in Figures S1–S3 of the Supplementary Materials. The Curve Fitting Tool in MATLAB version R2018a was used with the trust-region-reflective algorithm and nonlinear least square method. The resulting free coefficients are summarised in Table S3 of the Supplementary Materials. With the experimental process parameters listed in Table 1 as inputs, the quadratic model was developed with the QR decomposition algorithm using the iterative reweighted least square method in Statistics and Machine Learning Toolbox, MATLAB version R2018a.
The proposed DANN modelling framework is shown in Figure 1, using a static ANN model for the geometric prediction of a single-track profile in CSAM. The DANN was developed to predict a polar length at a polar angle from the Tool Centre Point (TCP). A data-driven model for predicting a complete single-track profile can be developed by sampling a sufficient number of geometric points from the fabricated single-track profiles, as demonstrated by the area validation method in our previous work [31]. The polar length was sampled at 2.72° intervals around the TCP, resulting in 67 points from each single-track profile.
Two data-efficient techniques were adopted in the proposed modelling framework, leveraging the Gaussian function model as an existing model, discussed above, to develop an ANN model. In Technique 1, the polar length approximated from the Gaussian function model was used as another input variable in addition to spray angle, traverse speed, standoff distance and polar angle. This technique explicitly leverages the partial domain knowledge of cold spray deposition, represented by the previously proposed Gaussian function model. At the same time, the DANN model learnt to compensate for the discrepancies between this knowledge and the true CSAM process, as successfully observed in other physical science fields [41,42]. Technique 2 was the augmentation of training data with a virtual input–output subset generated by the Gaussian function model. Therefore, the overall training dataset consisted of an empirical dataset prepared using the DOE method in Section 2.1 and a virtual dataset created using the Gaussian function model. The virtual dataset was generated from Gaussian function profiles using identical CSAM process parameters to those employed to make the physical test tracks and comprised of 804 training data points (i.e., 67 geometric sampling points from 12 simulated Gaussian function profiles). Both Technique 1 and 2 were independently employed in the preparation of training data and then simultaneously utilised in the development of the proposed DANN model.
For the development of the DANN model, this study iteratively changed the hidden layer architecture with the different number of hidden neurons (i.e., 1–15 neurons) per hidden layer and of hidden layers (i.e., 1–2 layers) to determine the optimal architecture using Mean Squared Error (MSE) as a performance evaluation function on an independent testing dataset. This range of hidden structures and evaluation function were selected given the limited data availability and frequent use in relevant studies respectively [29,30]. Following the 75–25 division method for the training-testing dataset, 12 single-track profiles were fabricated using the experimental methods described in Section 2.1 to form the testing dataset. The experimental process parameters for these testing profiles were randomly determined within the boundary of each parameter in Table 1 with the aid of the default random number generator in MATLAB version R2018a, summarised in Table S2 of the Supplementary Materials. Due to the limited training data, Bayesian regularised back-propagation was selected as the training method, eliminating the need for a validation dataset [43]. With this training method, hyperbolic tangent sigmoid and linear activation functions were selected for hidden and output layers, respectively, and all input and output variables were scaled to [−1 1] for improving a training process [44]. The training of a DANN model was performed using the Deep Learning Toolbox in MATLAB version R2018a. Each architecture candidate was retrained 100 times to avoid local optima convergence due to initially allocated weights and biases. A purely data-driven ANN model was also developed for comparison in predictive performance, using the same methods presented above for the DANN model. The difference was two-fold: (1) the number of input variables was four without the approximated polar length by the Gaussian function model, and (2) only the original training dataset prepared from the experimental single-track profiles was used.

3. Results

The quality of the fabricated single-track profiles was validated against the cold spray and CSAM studies in our previous study [31], confirming that each process parameter’s effects were consistent with previous relevant studies for the geometry of a single-track profile. Therefore, relevant and meaningful datasets could be generated from these single-track profiles that contained true representation of the CSAM process.

3.1. Data-Efficient Artificial Neural Network Model Validation

The Gaussian function model was built and evaluated on the coefficients taken from the testing single-track profiles (listed in Table S4 of the Supplementary Materials), showing the mean absolute error of 6.407%.
The iterative investigation of different hidden layer architectures found that the proposed DANN model, having two hidden layers with 11 and 4 hidden neurons respectively, provided the best predictive performance (i.e., [5 11 4 1]). During the training process, an MSE of 1.032 × 10−4 was achieved on the normalised independent testing dataset. The normalised predictive results are shown in Figure 2a with the resulting Mean Absolute Percent Error (MAPE) of 1.230% and Maximum Absolute Percent Error (MXAPE) of 5.748%. These predictive performances were comparable to another study of data-efficient machine learning modelling in manufacturing, e.g., MAPE of 5.483% [32]. Figure 2b shows the developed DANN model’s training process, confirming that the model was free of overfitting and underfitting and achieved the best performance at 445 epochs (or training iterations). Consequently, these results demonstrate the successful application of a data-efficient data-driven modelling approach to predict a single-track profile in CSAM.

3.2. Data-Efficient Artificial Neural Network Model Evaluation and Comparison

The proposed DANN model, incorporating Techniques 1 and 2, was evaluated and compared with other modelling approaches, including a mathematical Gaussian function model [24] and a purely data-driven ANN model [31]. Here, the mathematical Gaussian function model was not the Gaussian function model used for the data-efficient ANN model as the existing model, but one with the optimal coefficients, listed in Table S4 of the Supplementary Materials, that were found through the curve-fitting method described in Section 2.2. The resulting model was referred to as the curve-fitted Gaussian function model and prepared to allow for the comparison of the proposed data-efficient ANN model against the best predictive performance that could be achieved using the previously proposed framework for mathematical Gaussian function modelling [24]. For the purely data-driven ANN model, the best performance was achieved with the architecture [4 5 7 1], resulting in an MSE of 3.852 × 10−3. Furthermore, to investigate the effectiveness of each data-efficient technique, the data-efficient ANN models built using Technique 1 or Technique 2 solely were evaluated and compared. The prediction results of each model are summarised in Table 2 in absolute percent error and visually presented in Figure 3.
Compared with the purely data-driven ANN model, the data-efficient ANN model with Technique 1 or 2 alone showed better predictive performance with lower MAPEs and MXAPEs. This result indicates that both Technique 1 and 2 effectively achieved data-efficient learning and development of a data-driven ANN model. Furthermore, Technique 1 was more effective than Technique 2, with a MAPE half that of Technique 2. This result might be attributed to Technique 1 being more direct in guiding the learning process of weights and biases through the approximated target output (or polar length) than augmentation of the training dataset.
Hence, the proposed DANN model that combined the two data-efficient techniques achieved better predictive performance than the purely data-driven ANN model, showing that all of the prediction errors fell below the MAPE of the purely data-driven ANN model. The DANN model was also found to outperform the curved-fitted Gaussian function model with a lower MAPE and MXAPE. Notably, there was a lower number of predictions with large absolute percent errors (i.e., narrower upper quartile), as seen in Figure 3. This predictive capability became more significant when the entire single-track profile was predicted in the CSAM profiles, as presented in Figure 4.
Figure 4 shows the single-track profile of the two selected testing samples as an illustration: (a) symmetric Sample 48 at a normal spray angle of 90° and (b) asymmetric Sample 39 at an off-normal spray angle of 39°. The prediction results of all other testing profiles are shown in Figure S4 in the Supplementary Materials. It was observed that the purely data-driven ANN model showed a higher track profile in Sample 48 and physically inconsistent predictions around the peak region in Sample 39. In contrast, the proposed DANN model outperformed in these regions. This result suggests that the lower prediction accuracy caused by the data-scarcity around profile peak regions, as also identified in our previous study [31], was overcome in this study by using the data-efficient techniques.
Compared with the curve-fitted Gaussian function model, the DANN model showed better predictive performance in both illustrative cases in Figure 4. For the symmetric Sample 48, the single-track profile was rather a triangular-shape, as previously observed in other cold spray studies [26,27], resulting in the curve-fitted Gaussian function model showing cyclic errors across the entire single-track profile. For the asymmetric Sample 39, the curve-fitted Gaussian function model showed a larger deviation on the spray-tilted side (i.e., the right end of the profile). In this particular region of single-track profiles, the particles land on the deposit closer to the normal angle, which combined with a shorter effective standoff distance results in an increased local accumulation in the deposit with improved deposition efficiency [26]. In contrast, the proposed DANN model could capture this physical phenomenon and predict significantly better at the profile end regions in Figure 4.

4. Conclusions

This study presented the application of a data-driven modelling approach with two techniques for leveraging the existing model at hand (i.e., the Gaussian function model as a demonstration) to achieve data-efficient learning and development of a new ANN model. The comparative study was performed for the prediction of the testing single-track profiles in CSAM; both DANN models with Technique 1 or 2 alone outperformed the purely data-driven ANN model with lower MAPE and MXAPE, demonstrating the effectiveness of the data-efficient techniques. Furthermore, the proposed DANN model, incorporating both Techniques 1 and 2, was compared against the curve-fitted Gaussian function model and found to provide better predictive performance. This result demonstrates that a data-driven modelling approach can outperform a conventionally used mathematical function model in CSAM, both at normal and off-normal spray angles, with appropriate data-efficient modelling techniques. Moreover, these techniques harnessed the existing model in developing a new data-driven ANN model without further experimentation. This result may indicate that previously built models of HPRAM can be improved by following this study’s modelling strategy. In future works, we plan to incorporate the developed data-efficient ANN model into our toolpath planning algorithm to improve geometric control and achieve more complex-shaped product designs in cold spray additive manufacturing.

Supplementary Materials

The following are available online at https://www.mdpi.com/2076-3417/11/4/1654/s1, Figure S1: the experimental single-track profile S1–S12, Figure S2: the experimental single-track profile S13–S24, Figure S3: the experimental single-track profile S25–S36, Figure S4: the experimental single-track profile S37–S48 with the prediction of all models presented in this study, Table S1: Process parameters for the single-track profiles S1–S36 in the training dataset, Table S2: Process parameters for the single-track profiles S37–S48 in the testing dataset, Table S3: Curve-fitted coefficients of mathematical Gaussian function model for the single-track profiles S1–S36, Table S4: Curve-fitted coefficients of mathematical Gaussian function model for the single-track profiles S37–S48.

Author Contributions

Conceptualization, D.I.; methodology, D.I.; software, D.I.; validation, D.I.; formal analysis, D.I.; investigation, D.I.; resources, D.I., A.V.-U. and P.C.K.; data curation, D.I.; writing—original draft preparation, D.I.; writing—review and editing, D.I., A.V.-U., and P.C.K.; visualization, D.I.; supervision, X.W. and P.C.K.; project administration, D.I. and P.C.K.; funding acquisition, D.I., A.V.-U. and P.C.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by CSIRO’s Active Integrated Matter Future Science Platform (AIM–FSP) under the testbed number: WP10_TB04 and Research Training Program (International) Scholarship awarded to the first author from Department of Education, Skills and Employment, Australia.

Informed Consent Statement

Not applicable.

Acknowledgments

We would like to acknowledge and thank CSIRO Characterisation for access to LEXT OLS4000 confocal laser scanning microscope.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gärtner, F.; Stoltenhoff, T.; Schmidt, T.; Kreye, H. The cold spray process and its potential for industrial applications. J. Therm. Spray Technol. 2006, 15, 223–232. [Google Scholar] [CrossRef]
  2. Karthikeyan, J. The advantages and disadvantages of the cold spray coating process. In The Cold Spray Materials Deposition Process; Champagne, V.K., Ed.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 62–71. ISBN 978-1-84569-181-3. [Google Scholar]
  3. Villafuerte, J. Current and future applications of cold spray technology. Met. Finish. 2010, 108, 37–39. [Google Scholar] [CrossRef]
  4. Luo, X.-T.; Li, C.-X.; Shang, F.-L.; Yang, G.-J.; Wang, Y.-Y.; Li, C.-J. High velocity impact induced microstructure evolution during deposition of cold spray coatings: A review. Surf. Coat. Technol. 2014, 254, 11–20. [Google Scholar] [CrossRef]
  5. Sova, A.; Grigoriev, S.; Okunkova, A.; Smurov, I. Potential of cold gas dynamic spray as additive manufacturing technology. Int. J. Adv. Manuf. Technol. 2013, 69, 2269–2278. [Google Scholar] [CrossRef]
  6. Pathak, S.; Saha, G. Development of sustainable cold spray coatings and 3D additive manufacturing components for repair/manufacturing applications: A critical review. Coatings 2017, 7, 122. [Google Scholar] [CrossRef] [Green Version]
  7. Li, W.; Yang, K.; Yin, S.; Yang, X.; Xu, Y.; Lupoi, R. Solid-state additive manufacturing and repairing by cold spraying: A review. J. Mater. Sci. Technol. 2018, 34, 440–457. [Google Scholar] [CrossRef]
  8. Yin, S.; Cavaliere, P.; Aldwell, B.; Jenkins, R.; Liao, H.; Li, W.; Lupoi, R. Cold spray additive manufacturing and repair: Fundamentals and applications. Addit. Manuf. 2018, 21, 628–650. [Google Scholar] [CrossRef]
  9. Aggour, K.S.; Gupta, V.K.; Ruscitto, D.; Ajdelsztajn, L.; Bian, X.; Brosnan, K.H.; Kumar, N.C.; Dheeradhada, V.; Hanlon, T.; Iyer, N.; et al. Artificial intelligence/machine learning in manufacturing and inspection: A GE perspective. MRS Bull. 2019, 44, 545–558. [Google Scholar] [CrossRef]
  10. Mutombo, K. Research and development of Ti and Ti alloys: Past, present and future. IOP Conf. Ser. Mater. Sci. Eng. 2018, 430, 0120071–0120076. [Google Scholar] [CrossRef]
  11. Titomic Titomic Kinetic FusionTM. Available online: https://www.titomic.com/titomic-kinetic-fusion.html (accessed on 22 March 2019).
  12. Barnett, B.; Trexler, M.; Champagne, V. Cold sprayed refractory metals for chrome reduction in gun barrel liners. Int. J. Refract. Met. Hard Mater. 2015, 53, 139–143. [Google Scholar] [CrossRef] [Green Version]
  13. Cormier, Y.; Dupuis, P.; Jodoin, B.; Corbeil, A. Pyramidal fin arrays performance using streamwise anisotropic materials by cold spray additive manufacturing. J. Therm. Spray Technol. 2016, 25, 170–182. [Google Scholar] [CrossRef] [Green Version]
  14. Lynch, M.E.; Gu, W.; El-Wardany, T.; Hsu, A.; Viens, D.; Nardi, A.; Klecka, M. Design and topology/shape structural optimisation for additively manufactured cold sprayed components. Virtual Phys. Prototyp. 2013, 8, 213–231. [Google Scholar] [CrossRef]
  15. Ma, G.; Zhao, G.; Li, Z.; Yang, M.; Xiao, W. Optimization strategies for robotic additive and subtractive manufacturing of large and high thin-walled aluminum structures. Int. J. Adv. Manuf. Technol. 2019, 101, 1275–1292. [Google Scholar] [CrossRef]
  16. Li, Y.; Li, X.; Zhang, G.; Horváth, I.; Han, Q. Interlayer closed-loop control of forming geometries for wire and arc additive manufacturing based on fuzzy-logic inference. J. Manuf. Process. 2020. [Google Scholar] [CrossRef]
  17. Liu, H.; Qin, X.; Huang, S.; Jin, L.; Wang, Y.; Lei, K. Geometry characteristics prediction of single track cladding deposited by high power diode laser based on genetic algorithm and neural network. Int. J. Precis. Eng. Manuf. 2018, 19, 1061–1070. [Google Scholar] [CrossRef]
  18. Gonçalves, D.A.; Stemmer, M.R.; Pereira, M. A convolutional neural network approach on bead geometry estimation for a laser cladding system. Int. J. Adv. Manuf. Technol. 2020, 106, 1811–1821. [Google Scholar] [CrossRef]
  19. Frazier, W.E. Metal additive manufacturing: A review. J. Mater. Eng. Perform. 2014, 23, 1917–1928. [Google Scholar] [CrossRef]
  20. Ding, D.; Pan, Z.; Cuiuri, D.; Li, H. A multi-bead overlapping model for robotic wire and arc additive manufacturing (WAAM). Robot. Comput. Integr. Manuf. 2015, 31, 101–110. [Google Scholar] [CrossRef] [Green Version]
  21. Nenadl, O.; Kuipers, W.; Koelewijn, N.; Ocelík, V.; de Hosson, J.T.M. A versatile model for the prediction of complex geometry in 3D direct laser deposition. Surf. Coat. Technol. 2016, 307, 292–300. [Google Scholar] [CrossRef]
  22. Suryakumar, S.; Karunakaran, K.P.; Bernard, A.; Chandrasekhar, U.; Raghavender, N.; Sharma, D. Weld bead modeling and process optimization in Hybrid Layered Manufacturing. Comput. Des. 2011, 43, 331–344. [Google Scholar] [CrossRef]
  23. Xiong, J.; Zhang, G.; Gao, H.; Wu, L. Modeling of bead section profile and overlapping beads with experimental validation for robotic GMAW-based rapid manufacturing. Robot. Comput. Integr. Manuf. 2013, 29, 417–423. [Google Scholar] [CrossRef]
  24. Chen, C.; Xie, Y.; Verdy, C.; Liao, H.; Deng, S. Modelling of coating thickness distribution and its application in offline programming software. Surf. Coat. Technol. 2017, 318, 315–325. [Google Scholar] [CrossRef]
  25. Wu, H.; Xie, X.; Liu, M.; Chen, C.; Liao, H.; Zhang, Y.; Deng, S. A new approach to simulate coating thickness in cold spray. Surf. Coat. Technol. 2020, 382, 125151. [Google Scholar] [CrossRef]
  26. Kotoban, D.; Grigoriev, S.; Okunkova, A.; Sova, A. Influence of a shape of single track on deposition efficiency of 316L stainless steel powder in cold spray. Surf. Coat. Technol. 2017, 309, 951–958. [Google Scholar] [CrossRef]
  27. Klinkov, S.V.; Kosarev, V.F.; Shikalov, V.S. Influence of nozzle velocity and powder feed rate on the coating mass and deposition efficiency in cold spraying. Surf. Coat. Technol. 2019, 367, 231–243. [Google Scholar] [CrossRef]
  28. Zhu, W.; Zhang, X.; Zhang, M.; Tian, X.; Li, D. Integral numerical modeling of the deposition profile of a cold spraying process as an additive manufacturing technology. Prog. Addit. Manuf. 2019, 4, 357–370. [Google Scholar] [CrossRef]
  29. Deng, J.; Xu, Y.; Zuo, Z.; Hou, Z.; Chen, S. Bead geometry prediction for multi-layer and multi-bead wire and arc additive manufacturing based on XGBoost. In Transactions on Intelligent Welding Manufacturing; Chen, S., Zhang, Y., Feng, Z., Eds.; Springer: Singapore, 2019; pp. 125–135. ISBN 978-981-13-8667-1. [Google Scholar]
  30. Xiong, J.; Zhang, G.; Hu, J.; Wu, L. Bead geometry prediction for robotic GMAW-based rapid manufacturing through a neural network and a second-order regression analysis. J. Intell. Manuf. 2014, 25, 157–163. [Google Scholar] [CrossRef]
  31. Ikeuchi, D.; Vargas-Uscategui, A.; Wu, X.; King, P.C. Neural network modelling of track profile in cold spray additive manufacturing. Materials 2019, 12, 2827. [Google Scholar] [CrossRef] [Green Version]
  32. Liu, M.; Zhang, Y.; Dong, W.; Yu, Z.; Liu, S.; Gomes, S.; Liao, H.; Deng, S. Grey modeling for thermal spray processing parameter analysis. Grey Syst. Theory Appl. 2020, 10, 265–279. [Google Scholar] [CrossRef]
  33. Olleak, A.; Xi, Z. Calibration and validation framework for selective laser melting process based on multi-fidelity models and limited experiment data. J. Mech. Des. 2020, 142, 1–13. [Google Scholar] [CrossRef]
  34. Shafi, I.; Ahmad, J.; Shah, S.I.; Kashif, F.M. Impact of varying neurons and hidden layers in neural network architecture for a time frequency application. In Proceedings of the 2006 IEEE International Multitopic Conference, Islamabad, Pakistan, 23–24 December 2006; pp. 188–193. [Google Scholar]
  35. May, R.; Dandy, G.; Maier, H. Review of input variable selection methods for artificial neural networks. In Artificial Neural Networks—Methodological Advances and Biomedical Applications; InTech: London, UK, 2011; pp. 19–44. ISBN 9789533072432. [Google Scholar]
  36. Cai, Z.; Deng, S.; Liao, H.; Zeng, C.; Montavon, G. The effect of spray distance and scanning step on the coating thickness uniformity in cold spray process. J. Therm. Spray Technol. 2014, 23, 354–362. [Google Scholar] [CrossRef]
  37. Evjemo, L.D.; Moe, S.; Gravdahl, J.T.; Roulet-Dubonnet, O.; Gellein, L.T.; Brøtan, V. Additive manufacturing by robot manipulator: An overview of the state-of-the-art and proof-of-concept results. In Proceedings of the IEEE International Conference on Emerging Technologies and Factory Automation ETFA, Limassol, Cyprus, 12–15 September 2017; Volume 99, pp. 1–8. [Google Scholar]
  38. Noriega, A.; Blanco, D.; Alvarez, B.J.; Garcia, A. Dimensional accuracy improvement of FDM square cross-section parts using artificial neural networks and an optimization algorithm. Int. J. Adv. Manuf. Technol. 2013, 69, 2301–2313. [Google Scholar] [CrossRef]
  39. Green, A. Cold Spray Heats Up. Available online: https://blog.csiro.au/cold-spray-heats-up/ (accessed on 4 February 2021).
  40. Krishaniah, K.; Shahabudeen, P. Fundamentals of experimental design. In Applied Design of Experiments and Taguchi Methods; PHI Learning Pvt. Ltd.: New Delhi, India, 2012; pp. 22–48. ISBN 978-81-203-4527-0. [Google Scholar]
  41. Karpatne, A.; Watkins, W.; Read, J.; Kumar, V. Physics-guided Neural Networks (PGNN): An application in lake temperature modeling. arXiv 2017, arXiv:1710.11431. [Google Scholar]
  42. Deist, T.M.; Patti, A.; Wang, Z.; Krane, D.; Sorenson, T.; Craft, D. Simulation-assisted machine learning. Bioinformatics 2019, 35, 4072–4080. [Google Scholar] [CrossRef]
  43. Burden, F.; Winkler, D. Bayesian regularization of neural networks. In Methods in Molecular Biology (Clifton, N.J.); Springer: Berlin, Germany, 2008; Volume 458, pp. 25–44. [Google Scholar]
  44. Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education, Inc.: London, UK, 2009; ISBN 0131471392. [Google Scholar]
Applsci 11 01654 g001 550
Figure 1. The proposed data-efficient artificial neural network modelling framework for the prediction of a single-track profile in cold spray additive manufacturing. The CSAM process part represents a digital version of the experimental equipment and setup described in Section 2.1.
Figure 1. The proposed data-efficient artificial neural network modelling framework for the prediction of a single-track profile in cold spray additive manufacturing. The CSAM process part represents a digital version of the experimental equipment and setup described in Section 2.1.
Applsci 11 01654 g001
Applsci 11 01654 g002 550
Figure 2. The results of the developed data-efficient neural network model with [5 11 4 1] architecture: (a) normalised data-efficient ANN predictions vs. target outputs (or polar lengths) with a Mean Squared Error (MSE) of 1.032 × 10−4; (b) the training process of the developed data-efficient ANN model, showing no overfitting and underfitting.
Figure 2. The results of the developed data-efficient neural network model with [5 11 4 1] architecture: (a) normalised data-efficient ANN predictions vs. target outputs (or polar lengths) with a Mean Squared Error (MSE) of 1.032 × 10−4; (b) the training process of the developed data-efficient ANN model, showing no overfitting and underfitting.
Applsci 11 01654 g002
Applsci 11 01654 g003 550
Figure 3. Graphical summary of the prediction results in absolute percent error for the testing single-track profiles in Cold Spray Additive Manufacturing (CSAM). The proposed data-efficient Artificial Neural Network (ANN) model is shown as Tech. 1 + 2 data-efficient model.
Figure 3. Graphical summary of the prediction results in absolute percent error for the testing single-track profiles in Cold Spray Additive Manufacturing (CSAM). The proposed data-efficient Artificial Neural Network (ANN) model is shown as Tech. 1 + 2 data-efficient model.
Applsci 11 01654 g003
Applsci 11 01654 g004 550
Figure 4. The experimental single-track profiles of the two selected profiles in the testing dataset as illustrative cases (black), plotted with the corresponding prediction results of the curve-fitted Gaussian function model (blue), purely data-driven ANN model (green) and the data-efficient ANN model (red): (a) Sample 48 (spray angle: 90°, traverse speed: 39 mm/s, standoff distance: 39 mm) and (b) Sample 39 (spray angle: 39°, traverse speed: 34 mm/s, standoff distance: 41 mm).
Figure 4. The experimental single-track profiles of the two selected profiles in the testing dataset as illustrative cases (black), plotted with the corresponding prediction results of the curve-fitted Gaussian function model (blue), purely data-driven ANN model (green) and the data-efficient ANN model (red): (a) Sample 48 (spray angle: 90°, traverse speed: 39 mm/s, standoff distance: 39 mm) and (b) Sample 39 (spray angle: 39°, traverse speed: 34 mm/s, standoff distance: 41 mm).
Applsci 11 01654 g004
Table
Table 1. The levels of process variables in the experimental design matrix for the preparation of single-track profiles used for the training of the proposed data-efficient neural network model.
Table 1. The levels of process variables in the experimental design matrix for the preparation of single-track profiles used for the training of the proposed data-efficient neural network model.
LevelSpray Angle (°)Traverse Speed (mm/s)Standoff Distance (mm)
1452530
26010040
37520050
490--
Table
Table 2. Summary of the prediction results in absolute percent error for the testing single-track profiles in CSAM. The results are presented for: data-efficient ANN with the two techniques applied individually (Tech. 1 and Tech. 2), both applied (Tech. 1 + 2) also presented in Figure 2, curve-fitted Gaussian function model and purely data-driven ANN model. R2 values are also listed.
Table 2. Summary of the prediction results in absolute percent error for the testing single-track profiles in CSAM. The results are presented for: data-efficient ANN with the two techniques applied individually (Tech. 1 and Tech. 2), both applied (Tech. 1 + 2) also presented in Figure 2, curve-fitted Gaussian function model and purely data-driven ANN model. R2 values are also listed.
Absolute
Error %		Data-efficient ANNCurve-Fitted GaussianPurely Data-Driven ANN
Tech. 1Tech. 2Tech. 1 + 2
Mean2.0604.0401.2301.8737.174
Minimum0.0030.0030.0060.0010.060
Lower Q0.81471.1130.37240.26822.510
Median1.7192.7950.90810.82045.306
Upper Q3.0045.1731.7532.6199.831
Maximum9.68520.785.74811.8333.26
R20.99840.99640.99880.99310.9925
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Ikeuchi, D.; Vargas-Uscategui, A.; Wu, X.; King, P.C. Data-Efficient Neural Network for Track Profile Modelling in Cold Spray Additive Manufacturing. Appl. Sci. 2021, 11, 1654. https://doi.org/10.3390/app11041654

AMA Style

Ikeuchi D, Vargas-Uscategui A, Wu X, King PC. Data-Efficient Neural Network for Track Profile Modelling in Cold Spray Additive Manufacturing. Applied Sciences. 2021; 11(4):1654. https://doi.org/10.3390/app11041654

Chicago/Turabian Style

Ikeuchi, Daiki, Alejandro Vargas-Uscategui, Xiaofeng Wu, and Peter C. King. 2021. "Data-Efficient Neural Network for Track Profile Modelling in Cold Spray Additive Manufacturing" Applied Sciences 11, no. 4: 1654. https://doi.org/10.3390/app11041654

APA Style

Ikeuchi, D., Vargas-Uscategui, A., Wu, X., & King, P. C. (2021). Data-Efficient Neural Network for Track Profile Modelling in Cold Spray Additive Manufacturing. Applied Sciences, 11(4), 1654. https://doi.org/10.3390/app11041654

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop