A Heart Rate Variability-Based Paroxysmal Atrial Fibrillation Prediction System

Abstract

Atrial fibrillation (AF) is characterized by totally disorganized atrial depolarizations without effective atrial contraction. It is the most common form of cardiac arrhythmia, affecting more than 46.3 million people worldwide and its incidence rate remains increasing. Although AF itself is not life-threatening, its complications, such as strokes and heart failure, are lethal. About 25% of paroxysmal AF (PAF) patients become chronic for an observation period of more than one year. For long-term and real-time monitoring, a PAF prediction system was developed with four objectives: (1) high prediction accuracy, (2) fast computation, (3) small data storage, and (4) easy medical interpretations. The system takes a 400-point heart rate variability (HRV) sequence containing no AF episodes as the input and outputs whether the corresponding subject will experience AF episodes in the near future (i.e., 30 min). It first converts an input HRV sequence into four image matrices via extended Poincaré plots to capture inter- and intra-person features. Then, the system employs a convolutional neural network (CNN) to perform feature selection and classification based on the input image matrices. Some design issues of the system, including feature conversion and classifier structure, were formulated as a binary optimization problem, which was then solved via a genetic algorithm (GA). A numerical study involving 6085 400-point HRV sequences excerpted from three PhysioNet databases showed that the developed PAF prediction system achieved 87.9% and 87.2% accuracy on the validation and the testing datasets, respectively. The performance is competitive with that of the leading PAF prediction system in the literature, yet our system is much faster and more intensively tested. Furthermore, from the designed inter-person features, we found that PAF patients often possess lower (~60 beats/min) or higher (~100 beats/min) heart rates than non-PAF subjects. On the other hand, from the intra-person features, we observed that PAF patients often exhibit smaller variations (≤5 beats/min) in heart rate than non-PAF subjects, but they may experience short bursts of large heart rate changes sometimes, probably due to abnormal beats, such as premature atrial beats. The other findings warrant further investigations for their medical implications about the onset of PAF.

1. Introduction

Atrial Fibrillation (AF) is the most common type of cardiac arrhythmia that affects the quality of human life all over the world [1]. The common symptoms of AF contain dizziness, chest pain, shortness of breath, and palpitations, and it causes strokes and heart-related complications. The estimated number of people with AF was 20.9 million men and 12.6 million women worldwide in 2010 [2], and was updated to a total of 46.3 million individuals in 2016 [3]. The prevalence of AF increases with age, and affects males more than females [4]. The early form of AF is paroxysmal AF (PAF), during which the AF episode is self-terminating (≤48 h), and it is usually treatable. On-time prediction of PAF can prevent its transformation into chronic AF, which leads to high morbidity and mortality rates [5].

Owing to the highly nonlinear and nonstationary nature of human heartbeat signals [6,7], the prediction of PAF onset via a signal-prediction approach (i.e., by predicting further heartbeat signals based on the existing ones and checking for AF episodes) is impractical. Instead, a feature-classification approach is more commonly adopted, in which one set of heartbeat signals acquired from PAF patients that contain no AF episodes but are known to exhibit AF episodes in the near future (say, within 30 min) are to be distinguished from the other set acquired from healthy subjects. In such an approach, various features that improve signal separability, as well as computational efficiency, are first extracted from the heartbeat signals. Then, a classifier is designed to distinguish the two sets of signals. In the last few decades, many methods have been proposed for the feature-classification approach. According to the signal source, they can be roughly classified into two categories: electrocardiogram (ECG)-based or heart rate variability (HRV)-based methods. In ECG-based methods, the detection of features such as P-wave morphology and P-wave variability is essential for premature atrial complexes (PAC) detection [8,9]. However, ECG monitoring devices that provide accurate signals for such features are hardly accessible outside health centers. Although ECG signals can be acquired from some wearable devices, they have not met the medical-grade demands.

On the other hand, HRV has become a widely used signal to diagnose/predict several cardiac diseases because it can be more easily extracted from ECG through successive QRS complexes than those features through P waves. In addition, HRV signals have been found to provide useful clues about the underlying cardiac diseases [10,11,12,13,14], not to mention that they require much less computation and storage than ECG. A feature-classification approach is commonly adopted in HRV-based methods. Features representing subtle changes in an HRV signal that are associated with the underlying cardiac disease are computed and then sent to a classifier for state determination. These features are usually derived from the time, frequency, and state-space domains [6,15,16,17,18,19,20,21,22,23,24,25,26,27]. Some approaches that used a combination of features [11,12] in different domains may require a considerable amount of computations and, hence, are not suitable for quick diagnosis. Moreover, previous approaches seldom considered inter- and intra-person differences. However, features such as absolute and relative heart rate variations may both contribute to the disease onset, perhaps in different facets.

Recently, deep learning models have been widely applied to various fields, including computer vision [28], speech recognition [29], and natural language processing [30], where their performances are comparable to, and in some cases surpass, human experts. One of the most popular models is the convolutional neural network (CNN), which has appealing performances, particularly in image classification. It outperforms many conventional classifiers, such as artificial neural network (ANN), k-nearest neighbors (KNN), and support vector machine (SVM), in medical image analysis [31]. Since we converted an HRV sequence into multiple 2-dimensional matrices to reveal useful features, CNN was adopted in our system for feature selection and classification.

In this work, we developed a PAF prediction system that achieved accurate prediction with 400-point (~5 min) HRV sequences. Intra- as well as inter-person features that are easy to compute and interpret were proposed. The developed system was trained, validated, and tested using three datasets excerpted from PhysioNet [32]. The system performance and some medical implications derived from the proposed features are discussed herein.

2. Materials and Methods

2.1. Data Collection

Three databases, the PAF Prediction Challenge Database (accessed on 20 November 2019), MIT-BIH Atrial Fibrillation Database (accessed on 11 March 2021), and MIT-BIH Normal Sinus Rhythm Database (accessed on 11 March 2021) from PhysioNet, were employed to construct our PAF prediction system. Digitized ECG signals along with machine-generated beat annotation are available for download in the three databases. The PAF Prediction Challenge Database was issued in 2001 for competition and has been a benchmark database ever since. To compare with similar systems in the literature, we used it for training and validation, and used the other two databases for testing our system. The PAF Prediction Challenge Database consists of 200 30 min HRV sequences from 53 PAF patients and 47 normal subjects (two sequences per person). Those sequences were split into training and validation datasets with a ratio of 80:20 in such a way that the same numbers of PAF and non-PAF subjects were in the validation dataset, and the two HRV sequences from a person were allocated to the same dataset. We then extracted non-PAF HRV sequences from the MIT-BIH Normal Sinus Rhythm Database and PAF HRV sequences from the MIT-BIH Atrial Fibrillation Database to test the performance of our system. The MIT-BIH Normal Sinus Rhythm Database includes 24 h ECG recordings of 18 subjects without significant arrhythmias. On the other hand, the MIT-BIH Atrial Fibrillation Database contains 10 h ECG recordings of 25 patients with atrial fibrillation (mostly paroxysmal). We removed the top and the bottom one-hour data in each recording to avoid unstable data points.

2.2. Signal Preprocessing

To convert the HRV sequences from the afore-mentioned ECG signals, we downloaded RR intervals (in the unit of sec/beat) for each of those ECG signals from PhysioBank ATM at https://archive.physionet.org/cgi-bin/atm/ATM (last accessed on 11 March 2021). Then, each HRV sequence (in the unit of beats/min) was converted from its corresponding RR intervals using 60/(RR intervals). According to PhysioBank, the locations of the R waves in an ECG signal were determined by a QRS detector that used a modified Pan and Tompkins algorithm [33,34]. In the algorithm, a bandpass filter composed of cascaded low-pass and high-pass filters was applied to an ECG signal to reduce the influences of muscle noise, 60 Hz interference, baseline wander, and T-wave interference. The desirable passband was set to approximately 5–15 Hz in order to maximize the QRS energy [35,36]. A testing result showed that the accuracies of the QRS detection algorithm were generally >95% on multiple ECG databases acquired from bedside monitors when the subjects were in a resting state [37]. No further filtering in the frequency domain was applied to the HRV sequences for two reasons. Firstly, an HRV sequence is an uneven sampling (i.e., RR intervals) from ECG. It is difficult to interpret a certain frequency band in the frequency transformation of HRV. Secondly, the HRV sequence has been shown to exhibit a continuous spectrum [6]. Without knowing the exact sources of the noise, any filtering in the frequency domain can introduce artifacts into the sequence. However, certain countermeasures did apply in the feature conversion stage to reduce the noise caused by inaccurate QRS detections, which will be covered in the next section.

For the PAF Prediction Challenge Database, each 30 min HRV sequence was further divided into six 400-point subsequences, and overlapping was allowed if the sequence was less than 2400 points. As a result, 960 and 240 400-point HRV sequences were attained in the training and validation sets, respectively. The purpose of the division was not only to increase the dataset size, but also to reduce the data length for less computation and storage so that the constructed prediction system could be applicable to wearable devices. For the MIT-BIH Atrial Fibrillation Database, only episodes with 400 consecutive normal sinus beats (each beat is noted as “N” in the annotation file) and at least five consecutive normal sinus beats before and after the episodes were extracted from the two databases. Consequently, we acquired 3850 400-point HRV sequences from 18 healthy controls and 1035 400-point HRV sequences from 21 PAF patients (4 of the 25 patients in the database did not have a qualified episode). The detailed numbers of non-PAF and PAF HRV sequences in the training, validation, and testing datasets are listed in

Table 1. The number of non-PAF and PAF 400-point HRV sequences and the number of corresponding persons in our training, validation, and testing datasets.

Dataset	Non-PAF Sequences (Persons)	PAF Sequences (Persons)
Training	444 (37)	516 (46)
Validation	120 (10)	120 (10)
Testing	3850 (18)	1035 (21)

.

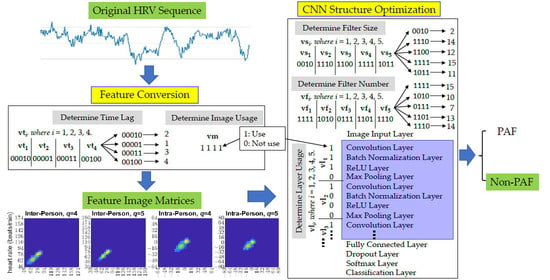
2.3. Feature Matrices Conversion

The purpose of this task is to convert each HRV sequence from its original data space into a feature space such that characteristics differentiating PAF from non-PAF data can be more explicitly revealed than in the original space. Let the dataset be made up of a set of m n-point HRV sequences, which can be denoted by X = [x₁, x₂, …, x_m], where x_i = [x_i,1, x_i,2,…, x_i,n]^T in the unit of beats/min, i = 1, 2, …, m. The process of constructing a feature matrix A ∈ $ℛ$^s×t from an HRV sequence $\mathrm{x} \in {ℝ}^n$ can be accomplished through a mapping function, Φ, such that A = Φ(x). In this work, we chose the discretized Poincaré plot to perform such a conversion for its easy construction, modification, and interpretation. In addition, it has been related to HRV physiology [38,39] and adopted for HRV analysis on PAF prediction for decades [11,13,40,41,42]. However, most of the previous works used features that measure only a certain facet of the plot and thus the information carried in the plot is not fully utilized. In fact, according to the definition of various abnormal beats in [43], these beats can be found in different regions in the Poincaré plot of an HRV sequence, as illustrated in Figure 1. More importantly, the discretized Poincaré plot of a sequence is shift-invariant in that the plot is independent of the feature locations in the sequence.

A Poincaré plot is a graph of x_i versus x_i+1 of a sequence, x = x₁, x₂, …, x_n, where I = 1, 2, …, n − 1. This plot is used to capture the correlation between two consecutive data points. It can be extended to calculate the correlation between sequential data points that are τ points away (lag), where τ is a positive integer less than n. Therefore, an n-point sequence can be represented by an extended Poincaré plot by drawing the points (x_i, x_i+τ) where i = 1, 2, …, n−τ. However, the Poincaré plot is a 2-dimensional real-valued image with an infinite number of points in a data-dependent range of [l_x, u_x] × [l_x, u_x], where l_x = min(x) and u_x = max(x). To generate a fixed-size matrix A ∈ ${\mathbb{N}}^{s\times s}$ for each HRV sequence, the range of allowable heart rates is to be defined, and then the resultant plot needs to be discretized before it can be used in the subsequent analysis. Let l_p and u_p represent accordingly the lower and the upper bounds of the heart rates to be included in the feature matrix A. The (i, j)-th component of the feature matrix, A(i, j), 1 ≤ i, j ≤ s, denotes the number of points lying within the region in the Poincaré plot defined by [l_p + (i − 1)q, l_p + iq] × [l_p + (j − 1)q, l_p + jq], where q = (u_p − l_p)/s is the quantization factor. The quantitation factor affects not only the heart rate range considered in our system, but also the level of noise tolerated by the system. In this design, the lower and the upper bounds of the Poincaré plot can be adjusted to reduce noise in an HRV sequence introduced by incorrect QRS detection. The missing and additional R waves due to incorrect QRS detection usually result in very low and very high heart rates accordingly that fall outside the normal resting heart rates (i.e., outliers), and thus can be removed by the bounds. On the other hand, the quantitation factor is useful in reducing noise caused by inaccurate QRS detection. This is because inaccurate QRS detection often leads to a small shift from its original value, which can be covered by a quantization window. The robustness of our system to the noise in the HRV sequences will be investigated in the discussion section.

Furthermore, the conventional Poincaré plot presents the absolute variations in the heart rate of the neighboring points in a sequence. In this case, a patient with a higher heart rate exhibits different features in the plot to those of another patient with a lower heart rate, even if their disease mechanisms are the same. To reduce the differences caused by the heart rate and focus on the relative heart rate variations among the sequence itself, we generated another Poincaré plot for each HRV sequence using the mean-removed sequence, $\widehat{x}=x-\overline{x}, \overline{x}={{\displaystyle \sum }}_{i=1}^n{x}_i$. Consequently, the original Poincaré plot was used to capture inter-person features, whereas the one generated from the mean-removed sequence was designed to tackle intra-person features. According to our preliminary studies, we set s = 32 and q = 4 and 5. As a result, four 32 × 32 feature matrices were generated for each input sequence. However, which matrices were actually input to the prediction system and their corresponding lags were determined by a genetic algorithm (GA). In this work, we derived the following formulas to convert an HRV sequence, x, from its original range to the feature matrix ranges.

$$x^{\prime }=\lfloor x-\left(110-q_i\ast \frac{s}{2}\right)/q_i\rfloor , i=1,2 (\mathrm{unit}: \mathrm{beats}/\min )$$

(1)

$${\widehat{x}}^{\prime }=\lfloor x-\overline{x}+\left(q_i\ast \frac{s}{2}\right)/q_i\rfloor , i=1,2 (\mathrm{unit}: \mathrm{beats}/\min )$$

(2)

2.4. Feature Selection and Classification

As all of the HRV sequences were being converted to two-dimensional featured matrices, a CNN was to be trained to classify the PAF feature matrices from non-PAF ones. The combination of techniques, such as mask convolution, normalization, ReLU activation function, and pooling (subsampling), and by arranging them into multiple replicates has enabled the CNN to extract effective features, which facilitates the subsequent classifications performed by a fully connected neural network.

However, the optimal structure of a CNN is problem-dependent. It usually starts with an input layer, followed by a few repeats of a layer set, including a convolution, a normalization, a ReLU, and a pooling layer, and ends up with several fully connected layers, a dropout layer, and a classification layer. Nevertheless, no clear guidelines are available for their suitable combinations. In our implementation, the above general structure was adopted, except that the number of repeats of the layer set, the involved layers in the layer set, the number of filters (or masks), and the filter size were determined by a GA. Noted that, although the actual involved layers in a layer set were determined by a GA, a convolution layer was always selected in the set, whereas the other layers were optional.

2.5. Parameter Determinations

As mentioned previously, a GA was employed to determine the parameters in feature conversion and in CNN structure optimization. A GA is a stochastic search algorithm for function optimization inspired by natural genetics. It begins with the random generation of an initial population of many individuals. An individual can be represented by either a binary or a real vector, depending on the applied problem. Each of the individuals in the population is then evaluated by a fitness function (the minimum of training accuracy and validation accuracy in this work). Individuals with better fitness values are more likely to be selected for mating. Each pair of selected individuals produces a pair of new individuals through crossover and mutation under some predetermined probabilities. The same population size is produced in each generation and some of the new individuals may exhibit better fitness values than those in the previous generation. The evolutionary process is continued until the maximum number of generations is reached. In real practice, the related settings are as follows: population size = 500, cross over rate = 0.85, mutation rate = 0.1, and the tournament method was used for individual selection.

In feature conversion, the time lags τ of the extended Poincaré plots and the usage of the four resultant feature matrices were determined by GA. Four time lags were correspondingly calculated by vt_i + 1, where vt_i, i = 1, 2, 3, 4, were binary vectors of length 5, making each time lag drawn from integers in the range of [1, 32]. The first two time lags were for the two inter-person feature matrices, whereas the latter two were for the two intra-person feature matrices. An additional binary vector, vm, of length 4 were used to control the usage (1 for use and 0 for not use) of the four feature matrices, resulting in a total of 24 binary numbers for feature conversion.

In CNN structure optimization, the layer usage in each layer set and the filter size and filter numbers in each convolution layer were determined by GA. Firstly, we assigned the maximum number of layer sets as 5, according to our preliminary studies. Then, five length-4 binary vectors, vl_i, i = 1, 2, 3, 4, 5, were employed to regulate the usage of the convolution layer, batch normalization layer, ReLU layer, and max-pooling layer sequentially in each of the layer sets. Finally, the number of filters and the size of the filters in the convolution layer of each layer set were determined accordingly via vf_i + 1 and vs_i + 1, where vf_i and vs_i, i = 1, 2, 3, 4, 5, were binary vectors of length 4, making the number of filters and the size of filters all drawn from integers in the range of [1, 16].

In summary, a length-84 binary vector v = [vt_i, vm, vl_j, vf_j, vs_j], i = 1, 2, 3, 4 and j = 1, 2, 3, 4, 5, selected by GA determined the parameters and the architecture of our PAF prediction system. Figure 2 shows the flowchart for the construction of the system. Let E_t(v) and E_v(v) denote accordingly the training error and the validation error of the system determined by a binary vector v, then the design of our PAF prediction system can be formulated as the following optimization problem.

$$\underset{v}{\min }\left(\max \left(E_t\left(v\right),E_v\left(v\right)\right)\right)$$

(3)

3. Results

3.1. Data Split

Recall that we employed two sets of extended Poincaré plots to capture inter- and intra-person features in a 400-point HRV sequence, respectively. In each set, two extended Poincaré plots, each with an individual quantization factor, were used to record features in different heart rate ranges and resolutions. Therefore, a total of four extended Poincaré plots were generated for each 400-point HRV signal. By using Equations (1) and (2) with the settings of s = 32 and q = 4 and 5, the covered heart rate ranges were [46, 174] and [30, 190] for the original HRV signals, and [−64, 64] and [−80, 80] for the mean-removed HRV. Since the HRV signals were extracted from ECG signals during normal sinus rhythm (both PAF and non-PAF subjects), the heart rate range of [30, 190] contained the majority (~99.8%) of the data points (refer to Appendix A Figure A1); thus, those points outside these ranges were most likely contaminated with noise or falsely measured and were ignored in the subsequent analysis.

3.2. The Converted Feature Matrices

Each filtered HRV sequence was then converted into four extended Poincaré plots. The four time lags, τ = 2, 1, 4, and 5, obtained from GA were used for the conversions. With these time lags, two extended Poincaré plots were accordingly generated from the original HRV signal with lags 2 and 1, and another two plots were generated from the mean-removed HRV signals with lags 4 and 5, respectively. Notably, the out–of–range data point and its corresponding lag point in the HRV signal were ignored during the conversion. With the matrix dimension s = 32 and the quantization factors q = 4 and 5, four Poincaré plots of ranges [46, 174] × [46, 174], [30, 190] × [30, 190], [−64, 64] × [−64, 64], and [−80, 80] × [−80, 80] were discretized to four 32 × 32 feature matrices. Since the binary vectors, vm, obtained from GA were all 1s, all four matrices were retained for the inputs of the subsequent CNN. Figure 3 presents the images of the four matrices generated from a non-PAF subject in the upper panel, whereas those generated from a PAF patient are presented in the lower panel.

3.3. Performance of the Developed PAF Prediction System

A five-layer CNN was selected by GA. The detail of the CNN structure is presented in Appendix A 

Table A1. The optimum structure of the CNN found by the GA approach.

No.	Name	Type	Activations	Learnables
1	imageinput 32 × 32 × 4 images with ‘zerocenter’ normalization	Image Input	32 × 32 × 4	-
2	conv_1 16 3 × 3 × 4 convolutions with stride [1 1] and padding ‘same’	Convolution	32 × 32 × 16	Weights 3 × 3 × 4 × 16 Bias 1 × 1 × 16
3	relu_1 ReLU	ReLU	32 × 32 × 16	-
4	conv_2 16 15 × 15 × 16 convolutions with stride [1 1] and padding ‘same’	Convolution	32 × 32 × 16	Weights 15 × 15 × 16 × 16 Bias 1 × 1 × 16
5	batchnorm_1 Batch normalization with 16 channels	Batch Normalization	32 × 32 × 16	Offset 1 × 1 × 16 Scale 1 × 1 × 16
6	conv_3 16 13 × 13 × 16 convolutions with stride [1 1] and padding ‘same’	Convolution	32 × 32 × 16	Weights 13 × 13 × 16 × 16 Bias 1 × 1 × 16
7	conv_4 14 16 × 16 × 16 convolutions with stride [1 1] and padding ‘same’	Convolution	32 × 32 × 14	Weights 16 × 16 × 16 × 14 Bias 1 × 1 × 14
8	batchnorm_2 Batch normalization with 14 channels	Batch Normalization	32 × 32 × 14	Offset 1 × 1 × 14 Scale 1 × 1 × 14
9	relu_2 ReLU	ReLU	32 × 32 × 14	-
10	conv_5 15 12 × 12 × 14 convolutions with stride [1 1] and padding ‘same’	Convolution	32 × 32 × 15	Weights 12 × 12 × 14 × 15 Bias 1 × 1 × 15
11	batchnorm_3 Batch normalization with 15 channels	Batch Normalization	32 × 32 × 15	Offset 1 × 1 × 15 Scale 1 × 1 × 15
12	relu_3 ReLU	ReLU	32 × 32 × 15	-
13	fc 2 fully connected layer	Fully Connected	1 × 1 × 2	Weights 2 × 15360 Bias 2 × 1
14	dropout 50% dropout	Dropout	1 × 1 × 2	-
15	softmax softmax	Softmax	1 × 1 × 2	-
16	classoutput crossentropyex with classes ‘0′ and ‘1′	Classification Output		-

. Moreover, the filter numbers and sizes were 16 3 × 3 filters in the first convolution layer, 16 15 × 15 filters in the second convolution layer, 16 13 × 13 filters in the third convolution layer, 14 16 × 16 filters in the fourth convolution layer, and 15 12 × 12 filters in the fifth convolution layer. In summary, our PAF prediction system achieved an accuracy of 100% in the training dataset, 87.9% in the validation set, and 87.2% in the testing set. Figure 4 depicts the confusion matrices for the training, validation, and testing datasets.

4. Discussion

4.1. Comparison with Similar Systems

Although some systems had achieved higher accuracies of more than 90%, they were based on 30 min or longer records [12].

Table 2. Similar studies in the literature.

Literature	Databases	Data Length (min)	Features	Cross-Validation	Results (%)
					SEN	SPE	ACC
Hickey and Henegham [44]	AFPDB	5	HRV power spectral density and PACs	5-fold	51.0	79.0	68.0
Chazal and Henegham [45]	AFPDB	5	P-wave power spectral density	5-fold	81.0	69.0	75.6
Boon et al. [9]	AFPDB	5	Combination of 9 HRV features in time and frequency domains	10-fold	86.8	88.7	87.7
Narin et al. [10]	AFPDB	5	Combination of 26 HRV features in time and frequency domains	10-fold	92.0	88.0	90.0
Mendez et al. (This study)	AFPDB * NSRDB * AFDB *	~5 (400 points)	32 × 32 × 4 images from extended and discretized Poincaré plot	Single-fold	80.4	89.0	87.2

* AFPDB, NSRDB, and AFDB are abbreviations for the PAF Prediction Challenge Database, MIT-BIH Normal Sinus Rhythm Database, and MIT-BIH Atrial Fibrillation Database, respectively.

shows a comparison of similar PAF prediction systems in the literature, in which predictions were made based on 5 min HRV sequences extracted from the PAF Prediction Challenge Database (AFPDB). We note that the second to the last group in the table claimed to achieve an accuracy of 90, but, in their paper, they indicated that such an accuracy was only attained when the HRV signals were 2.5–7.5 min prior to the onset of AF, whereas other episodes could only achieve around 85% accuracy [12]. The most competitive and promising result in the table thus leads to Boon’s system with an accuracy of 87.7% [11]. Such an accuracy is very close to our result of 87.9% in the validation set and 87.2% in the testing set. However, the accuracy of Boon’s system was obtained from a 10-fold cross-validation, in which the data were only drawn from the AFPDB. The same database was used as our training and validation sets. Yet, we tested our system on a much larger dataset with 4885 HRV sequences from two other databases and achieved a similar accuracy of 87.2%.

Furthermore, the features used in other systems in Table 2 consisted of time-domain and/or frequency-domain nonlinear features. These features are usually computationally intensive and their medical implications are rarely interpretable. In comparison, our system was able to perform prediction of 4885 400-point HRV sequences in the test dataset in an average (from 10 tests) of 6.1 s or 1.25 milliseconds per sequence under the MATLAB^® environment with an Intel^® Core™ i7-9750H CPU at 2.60 GHz and 32 GB RAM. In addition, because our features can directly link back to the original HRV sequence, their medical implications can be traced easily. Some of the implications from the designed inter- and intra-features are discussed next.

4.2. Medical Implications from the Features

Recall that we generated four feature matrices for the input of CNN by discretizing four extended Poincaré plots including two inter-person features and two intra-person features. We computed the average counts of each element in the four matrices for PAF patients and for non-PAF subjects. Then, the four averaged matrices of non-PAF subjects were subtracted accordingly from those of PAF patients, as shown in Figure 5. Consequently, the elements with larger differences (dark-red color in the image) are highly associated with the PAF patients and can be regarded as risk factors for AF. According to the inter-person feature matrices, PAF patients seem to have either a lower heart rate of around 60 beats/min or higher heart rate of around 100 beats/min, and they tend to exhibit more off-diagonal pixels (yellow pixels along the off-diagonal lines), indicating interchanges of fast–slow or slow–fast heart rates in the neighbor beats. In addition, from the intra-person feature matrices, PAF patients often have smaller heart rate variations ≤5 beats/min in the lag-4 and lag-5 sequences, but they may occasionally exhibit large heart rate changes of ≥20 beats/min (brighter pixels along the vertical and horizontal axes). Such phenomena coincided with our understanding since PAF patients tend to exhibit more irregular beat–to–beat intervals than non-PAF patients, as shown in Figure 6. For example, premature atrial beats are frequently observed in PAF patients [8], resulting in a short R-R interval followed by a prolonged R-R interval, which leads to a fast–slow heart rate change in an HRV sequence.

On the other hand, the pixels in dark-blue colors in Figure 5 are predominant in non-PAF subjects and they can be considered as protective factors from AF. From the inter-person feature matrices, non-PAF subjects tend to have a heart rate range of around 82–94 beats/min. Moreover, from the intra-person features, non-PAF subjects often exhibit medium heart rate changes of around 10 beats/min. However, such changes tend to increase from the average heart rate, rather than decrease. Other phenomena in Figure 5 also drew our attention. Nevertheless, their medical implications warrant further investigations.

4.3. Robustness of the System

As mentioned in Section 2.2, we attempted to reduce the noise resulting from inaccurate QRS detection by adjusting the upper and lower bounds and the quantization factor of the discretized Poincaré plot. To investigate the robustness of our PAF prediction system, we added various percentages of random noise to the HRV sequences and recorded the corresponding performance of the system. We note that the percentage of noise added to the HRV sequence was proportional to the median of the sequence, since some abnormal beats may be involved in the sequence, affecting the average and range of the sequence. Figure 7 shows the resulting changes in the prediction accuracy (Acc), true positive percentage (TPP), and true negative percentage (TNP) in the training, validation, and testing datasets, respectively. As shown in the figure, all the prediction accuracies remained ≥80% if no larger than 3% of noise was added to the HRV sequences.

4.4. Analysis of Misclassifications

We attempted to explore the causes of misclassifications of our PAF prediction system. Firstly, hierarchical clustering was adopted to find subgroups in PAF as well as in non-PAF HRV sequences. All the HRV sequences (4414 non-PAF and 1671 PAF) in the three datasets adopted in this study were used to obtain representative subgroups. The four 32 × 32 feature matrices for each sequence were flattened into a 4096 vector, and then the similarity among the sequences was measured by their Euclidean distances. The Ward’s method was applied to perform linkages among the converted vectors. The clustering result of the PAF HRV sequences and that of non-PAF sequences are provided in Appendix A Figure A2. Using a distance of 3500 as a cutting threshold, the PAF and non-PAF HRV sequences were divided into nine and six subgroups, respectively. Secondly, we further separated the sequences that were correctly identified from those that were falsely identified in each subgroup, resulting in a total of 30 subgroups. Thirdly, the converted vectors in each subgroup were averaged so that all of the HRV sequences were represented by 30 4096 vectors. Finally, the 30 vectors were again clustered using the Euclidean distances among them and the Ward’s linkage method. Figure 8 illustrates the clustering result. The symbols of TP, TN, FP, and FN in the figure denote true positive (PAF), true negative (non-PAF), false positive, and false negative, respectively. The number behind each group represents the group index, whereas the number in parentheses indicates the number of sequences in the corresponding subgroup. As shown in the figure, the false-negative HRV sequences were indeed apart from the true positive ones. Similar situations can be also observed among the true negative and false positive subgroups. Such phenomena suggest that the misclassified HRV sequences, either PAF or non-PAF, exhibit larger differences than the correctly identified ones and, hence, they are more likely to be misclassified. Such misclassifications may be inevitable, either due to large differences from their fellow sequences or due to measuring noise. By using shorter sequences and simpler features, we anticipate that our PAF prediction system can reduce misclassifications by integrating the classification results of neighboring HRV sequences.

4.5. Future Works

We shall continue to work with cardiologists to explore the medical implications of the designed inter- and intra-person features. In addition, we shall conduct an investigation about whether some of the features can be used to develop a scoring scheme, such that the confidence of the prediction can be calculated and be provided to the users. Furthermore, since the PAF Prediction Challenge Database also provides information about how far a 30 min ECG signal is away from an AF episode, we can study the predictability of the designed features toward the onset of PAF. With the information of the time to AF onset, data can be further divided into different time intervals to AF onset and then be used to train a PAF system to predict the distance (in time) to the AF onset. To increase the applicability of the system, data from patients with other arrhythmias should also be used to train and test the prediction system so that the system can differentiate PAF patients from not only healthy subjects, but also other arrhythmia patients.

5. Conclusions

In this paper, an HRV-based PAF prediction system was developed. We showed that the proposed PAF prediction system achieved 87.2% accuracy using 400-point (~5 min) HRV sequences. Although the accuracy was equivalent to that of the leading system in the literature, our system was more intensively tested (three large databases containing 608, 400-point HRV sequences), and had a faster prediction speed (1.25 millisecond per 400-point HRV sequence) and smaller storage requirement (<1 KB per 400-point HRV sequence). In addition to the system performance, we utilized a discretized Poincaré plot to represent the features in an HRV sequence; such features are easy to construct and, more importantly, their medical implications can be easily interpreted since they still possess a direct link to the original HRV sequence. Instead of investigating the relationship between two consecutive points in the conventional Poincaré plot, we further explored the relationship between two points that are some distance apart using a generalized Poincaré plot. We also used a generalized Poincaré plot to represent features from the original HRV sequence and its mean-removed sequence. Such a manipulation allows our system to explore the data from two (i.e., inter-person and intra-person) different aspects. Consequently, from the inter-person features, we found that PAF patients often possess lower (~60 beats/min) or higher (~100 beats/min) heart rates than non-PAF subjects. On the other hand, from the intra-person features, we observed that PAF patients often exhibit smaller variations (≤5 beats/min) in heart rate than non-PAF subjects, but they may experience short bursts of large heart rate changes sometimes, probably due to abnormal beats, such as premature atrial beats. Finally, we converted the Poincaré plot-based features into images and employed a CNN to select the crucial ones so as to distinguish PAF from non-PAF HRV sequences. Although the CNN has been shown to exhibit powerful image classification capabilities, training a new CNN is very time-consuming, not only to compute the weights in all of the network connections, but also to determine many parameters for the network structure. To determine suitable parameters in feature conversion (lag between data points and the number of input images) and in CNN construction, we adopted a GA approach, which is famous for its capability of finding near-global optimization solutions. As a result, we successfully constructed a PAF prediction system whose performance is competitive with the leading PAF prediction system in the literature. The system requires only Poincaré plot-based features and thus outperforms many existing systems in computation speed. Furthermore, we anticipate that such features can contribute to identifying key differences between PAF and non-PAF HRV sequences, which may thus help cardiologists to pinpoint PAF onset mechanisms and eventually facilitate AF prevention.