Double-Mode Thermometer Based on Photoluminescence of YbGd₂Al₂Ga₃O₁₂: Cr³⁺ Operating in the Biological Windows

Abstract

A Near-Infrared (NIR) ratiometric luminescence thermometer with the composition of Yb₁Gd₂Al_1.98Cr_0.02Ga₃O₁₂ was prepared and studied. When excited by 660 nm in the first biological transparent window (BTW), the sample shows a peak structure of around 1000 nm due to the ²F_5/2 → ²F_7/2 transitions of Yb³⁺ via the energy transfer process from Cr³⁺. Due to the Boltzmann distribution, the Yb³⁺ PL intensities in the shorter wavelength side (i.e., 1st BTW) and longer wavelength side (i.e., 2nd BTW) exhibit opposite temperature dependencies. The luminescence intensity ratio (LIR) of Yb³⁺ in shorter and longer wavelength ranges works as a luminescence thermometer with a relative sensitivity of 0.55% K⁻¹ at 310 K. In addition, YbGd₂Al_1.98Cr_0.02Ga₃O₁₂ can also be employed for temperature sensing based on the LIR of Cr³⁺ (²E → ⁴A₂) at around 700 nm and Yb³⁺ (²F_5/2 → ²F_7/2) at around 1000 nm, achieving a remarkable relative sensitivity of 2.69% at 100 K. This study confirms that the YbGd₂Al_1.98Cr_0.02Ga₃O₁₂ thermometer fulfills the requirements for biological temperature measurements.

1. Introduction

Since the 1980s, phototherapy and hyperthermia treatment in cancer therapy have attracted considerable attention due to their unique therapeutic effects [1,2,3,4]. Compared to chemotherapy and radiotherapy, these techniques have minimal side effects, further contributing to maintaining a high level of research interest. These treatments crucially require continuous monitoring of temperature distribution to avoid damaging normal cells, as deviations in temperature cause irreversible harm during treatment. Therefore, phototherapy and hyperthermia treatment should be accompanied by a real-time temperature measurement technique. Inorganic luminescence thermometers have emerged as a solution, offering real-time, rapid response and high sensitivity remote temperature measurements. Luminescence thermometers within the biological transparent window (BTW) are particularly advantageous for temperature detection from deep tissue. The BTW can be separated into three wavelength regions, 650–950 nm (1st), 1000–1350 nm (2nd), and 1550–1870 nm (3rd), which are summarized based on the spontaneous fluorescence, absorption effects from biological tissues, and the inverse fourth power of the Rayleigh scattering effect concerning the wavelength [5,6].

In the past two decades, for the research of luminescence thermometers, a widely employed strategy is the combination of the ratiometric method and Boltzmann distribution, which relies on the luminescence intensity ratio from two thermally coupled energy levels of the luminescence center ion in inorganic host material. The population of these two energy levels is determined by the Boltzmann distribution [7,8,9,10]. The most widely used Boltzmann thermometer is based on the thermally coupled energy levels of Er³⁺: ⁴S_3/2/²H_11/2. One of the interesting applications of it has been its use in measuring the local temperature gradients during catalytic reactions [11]. Furthermore, other luminescence ions have been investigated from the luminescence wavelength and temperature rage viewpoint. Boltzmann thermometers based on Ho³⁺: ⁵F₄/⁵F₅ [12,13], and Eu³⁺: ⁵D₀/⁵D₁ [14] have been gradually developed for high-temperature detection because of the high energy difference between these pairs of thermally coupled levels, exceeding 1500 cm⁻¹. However, these Boltzmann thermometers work within the visible range; when used for deep tissue temperature measurement, they are affected by Rayleigh scattering, spontaneous fluorescence from biological tissues, and absorption effects, leading to reduced temperature measurement accuracy.

NIR Boltzmann thermometers have become the hotspot for deep tissue temperature measurement in recent years. Nd³⁺ ion is often seen as an ideal NIR luminescence center for its excitation and emission within the BTW. However, the less-than-perfect energy differences (ΔE) between two pairs of thermally coupled energy levels of Nd³⁺ bring about a technical bottleneck for temperature measurement applications. Nd³⁺: ⁴F_3/2/⁴F_5/2 with a ΔE of up to 1000 cm⁻¹ results in a deviation from the theoretical LIR value after the temperature drops below 300 K [15]. On the other hand, the relative sensitivity of temperature measurement based on the thermally coupled Stark sublevels of Nd³⁺: ⁴F_3/2 is low due to a ΔE value as low as 100 cm⁻¹ (not exceeding 0.7% K⁻¹) [16,17,18]. Therefore, one approach to overcome this technical bottleneck is to find a NIR luminescence center with a moderately suitable ΔE value.

Yb³⁺-doped GAGG is more advantageous for luminescence temperature measurement applications. Yb³⁺ is a NIR luminescence center with a ΔE value of 300~680 cm⁻¹ for the Stark energy level pairs of the ²F_5/2 excited state [19,20]. This enables more accurate temperature measurements at lower temperatures than Nd³⁺. Among various hosts for Yb³⁺, Gd₃Al₂Ga₃O₁₂ (abbreviated as GAGG) allows the Yb³⁺ ions to have the highest optical conversion efficiency [21], and its thermal conductivity does not dramatically degrade compared to other pure garnets [22]. As a member of the garnet family, GAGG also has a broad transparency range, good thermomechanical properties, thermal stability, and chemical stability.

Transition metal Cr³⁺ has been repeatedly demonstrated to exhibit strong PL in various garnet hosts [23]. The Cr³⁺-Yb³⁺ pair also represents a dual-center system with energy transfer capabilities [24]. Compared to Yb³⁺ single-doped GAGG, the advantage of co-doping with Cr³⁺ is that visible light (e.g., at 660 nm, which is within the 1st BTW) can excite Cr³⁺ instead of directly exciting Yb³⁺ with infrared light. This approach enables the complete measurement of the Yb³⁺ PL spectrum.

A Yb³⁺ and Cr³⁺ co-doped Gd₃Al₂Ga₃O₁₂ (GAGG) NIR thermometer was developed in this work. The optical performance of the sample at 660 nm excitation is evaluated through temperature-dependent photoluminescence spectra and the fitting calculations. The shape of the Cr³⁺ PL spectra and the Cr³⁺ → Yb³⁺ energy transfer process are discussed with Racah parameter calculations and fitting of the luminescence lifetime, respectively. This work demonstrated that Yb³⁺ and Cr³⁺ co-doped GAGG thermometers have the potential for accurate temperature measurement in the field of biology.

2. Materials and Methods

The YbGd₂Al_1.98Cr_0.02Ga₃O₁₂ transparent ceramic was synthesized using the solid-state reaction method. Gd₂O₃ (4N), Yb₂O₃ (4N), Al₂O₃ (4N), Cr₂O₃ (3N), and Ga₂O₃ (4N) were used as starting materials. The mixed precursors were ball-milled with ethanol, and the obtained slurry was dried at 95 °C for 18 h. After drying, the powder was calcined at 1000 °C for 8 h, and then compressed into a pellet using a hydraulic press. Finally, the pellet was sintered at a high temperature of 1600 °C for 8 h in a vacuum environment. The obtained transparent ceramics were double-surface polished using a copper plate and diamond slurry.

The phase compositions of the synthesized powders and consolidated ceramics were determined via X-ray diffraction (XRD) (Ultima IV, Rigaku, Tokyo, Japan). Download GAGG’s standard xrd pattern from the Inorganic Crystal Structure Database (ICSD 5.1.0) library for comparison. One set of PL spectra was measured under 660 nm LED (Newport, Irvine, CA, USA) excitation with a 695 nm shortcut filter. The other set of PL spectra was measured under 455 nm LD excitation with a 570 nm shortcut filter (Optocode Corporation, Tokyo, Japan). PL spectra were detected using a multichannel spectrometer (NIR-Quest, Ocean Optics, Orlando, FL, USA) with a connected optical fiber. The obtained PL spectra were calibrated against a spectrum of deuterium−tungsten halogen light sources (DH-2000, Ocean Optics). The temperature of the sample was controlled by a thermal stage (10033L, Linkam, Redhill, UK) in the temperature range of 100–400 K. The absorption spectrum was obtained separately using a UV3600 Shimadzu spectrophotometer (Kyoto, Japan). The excitation source for the fluorescence lifetime test is an N₂ dye laser (KEC-200, USHO, Tokyo, Japan) with a coumarin dye (480 nm).

3. Results and Discussion

3.1. Crystal Structure

The X-ray diffraction pattern of the garnet sample YbGd₂Al_1.98Cr_0.02Ga₃O₁₂ (YbGAGG: Cr³⁺) and standard cubic-Gd₃Al₂Ga₃O₁₂ garnet (GAGG, ICSD No. 37571) [25] are shown in Figure 1. Sample is identified as a single phase of the garnet structure, and the XRD peaks are shifted to a slightly higher degree due to one-third of the Gd³⁺ ions being substituted by smaller Yb³⁺ ions.

To clarify the structure of the Cr³⁺ doped YbGd₂Al₂Ga₃O₁₂ sample, the Rietveld refinement on the XRD pattern of the sample within the General Structure Analysis System (GSAS) was performed (as shown in Figure 2). The refined agreement factors are as follows: Rp = 14.32%, Rwp = 19.52%. The space group of GAGG is Ia-3d and lattice parameter a = 12.257 Å, with the unit cell volume V = 1841.64 Å [25]. The refined result shows that, for the Cr³⁺ doped YbGd₂Al₂Ga₃O₁₂ sample, a = 12.110 Å, V = 1776.06 Å, with an unchanged Ia-3d space group. The result indicated that the unit cell volume of the sample is smaller than the GAGG host because of the smaller ionic radius of Yb³⁺ than that of Gd³⁺.

3.2. Luminescence Properties of YbGAGG: Cr³⁺

The absorbance coefficient spectrum of transparent ceramic YbGAGG: Cr³⁺ is shown in Figure 3a. The shape of the absorbance coefficient (α) spectrum in the 400–700 nm range aligns with the ⁴A₂-⁴T₁ and ⁴A₂-⁴T₂ absorption bands of Cr³⁺. On the contrary, at approximately 1000 nm, typical absorption peaks of Yb³⁺ are observed. Notably, the spectrum only shows absorption bands for Cr³⁺ and Yb³⁺, with no Cr⁴⁺ signal (at around 1350 nm). These results prove that the oxidation state of chromium in the YbGAGG host is trivalent.

The orange curve in Figure 3b represents the PL spectrum of the YbGAGG: Cr³⁺ sample under 660 nm excitation at room temperature. At approximately 1000 nm, the PL band of Yb³⁺: ²F_5/2 → ²F_7/2 was observed. The purple curve is the photoluminescence excitation (PLE) spectrum monitoring the PL of Yb³⁺. Two PLE bands within the 400–700 nm range were attributed to the transition from the ⁴A₂ to two excited states of Cr³⁺: ⁴T₁ and ⁴T₂ [26], confirming the energy transfer process from Cr³⁺ to Yb³⁺. For the PL spectrum (orange curve) in Figure 3b, no PL signal was observed in the 700–800 nm range (where the Cr³⁺ PL signal is expected). This result is attributed to the excessive concentration of Yb³⁺, leading to an efficient energy transfer process from Cr³⁺ to Yb³⁺.

To further investigate the energy transfer process from Cr³⁺ to Yb³⁺, a luminescence lifetime measurement of Cr³⁺ was performed and shown in Figure 4. The PL decay of both YbGAGG: Cr³⁺ and GAGG: Cr³⁺ (preparation method is the same as for YbGAGG: Cr³⁺) in the range of 600–800 nm were measured under 480 nm excitation. The obtained decay plots were fitted using the following double exponential function:

$$I=A_1\times exp(-t/{\tau }_1)+A_2\times exp(-t/{\tau }_2)$$

(1)

After fitting the decay curve with a function and obtaining the parameters, the lifetime is calculated using the following formula:

$${\tau }_{ave}=\frac{A_1{\tau }_1^2+A_2{\tau }_2^2}{A_1{\tau }_1+A_2{\tau }_2}$$

(2)

Using Formula (2), the lifetimes of the decay curves for YbGAGG:Cr³⁺ and GAGG:Cr³⁺ were calculated as τ_CrYb = 3.86 ms and τ_Cr = 0.122 ms, respectively. Substituting these values into the following formula, the energy transfer efficiency was calculated to be η = 96.8%:

$$\eta =1-{\tau }_{\mathrm{CrYb}}/{\tau }_{\mathrm{Cr}}$$

(3)

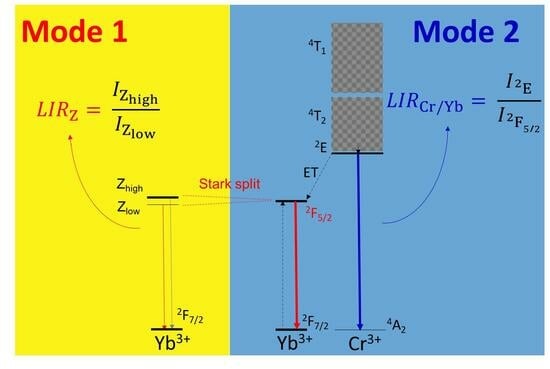
3.3. YbGAGG: Cr³⁺ Ratiometric Thermometer Based on the Emission of Yb³⁺ (Mode 1)

The temperature dependence of PL of YbGAGG: Cr³⁺ from 100 K to 400 K was measured and shown in Figure 5a. A notable observation is that the intensity of the central PL peak, located near 1026 nm (within the second BTW), decreases as the temperature increases. Furthermore, within the first BTW (650–950 nm), the PL spectra display an inverse temperature dependence compared with the central peak H in the more extended wavelength range. The reason for this phenomenon is the Stark splitting of the ²F_5/2 level of Yb³⁺ in the garnet, resulting in the separation into the lowest Stark sublevel (denoted as Z_low) and several higher ones (denoted as Z_high, typically containing two levels according to Kaminskii’s work [19]). Due to the Boltzmann distribution, the intensity of the PL from Z_high exhibits a positive correlation with temperature (corresponding to the short wavelength range before 1000 nm in Figure 5a).

To obtain the temperature dependence of the intensity of each PL peak of YbGAGG: Cr³⁺, a deconvolution analysis was performed on the PL spectra across a temperature range of 100–400 K. Examples of this analysis process are shown in Figure 5b. Detailed information on the temperature dependence of the peak center position and peak intensity for peaks labeled A–J were derived from deconvolution and are shown in Figure 5c,d.

After obtaining the temperature dependence of the position and intensity of each peak, peaks C and H, located in the first BTW and second BTW, respectively, were selected due to their contrasting temperature dependencies. These peaks were then utilized to determine the temperature dependence of the LIR. The temperature dependence of LIR = I_C/I_H (Mode 1) was calculated and shown in Figure 6a. The cubic polynomial function was employed to fit the temperature dependence of the LIR. Subsequently, absolute sensitivity (S_a) and relative sensitivity (S_r) were calculated using Equations (1) and (2), respectively.

$$S_{\mathrm{a}}=\frac{\mathrm{d}\left(LIR\right)}{\mathrm{d}T}$$

(4)

$$S_{\mathrm{r}}=\frac{1}{LIR}\times \frac{\mathrm{d}\left(LIR\right)}{\mathrm{d}T}\times 100\%$$

(5)

The calculated S_a and S_r curves are shown in Figure 6b. Notably, when the temperature reaches 122 K, S_r reaches its maximum value of 1.30% K⁻¹. This value exceeds the S_r of the Nd³⁺-based luminescence thermometer, which also utilizes Stark sublevels for temperature measurements but has a lower S_r maximum value of 0.7% K⁻¹ [17]. However, as the temperature increases above 122 K, S_r monotonically decreases, leaving a value of 0.55% K⁻¹ for S_r at 310 K. This trend indicates that Mode 1 of the YbGAGG: Cr³⁺ thermometer has the potential for application in biological temperature measurements and also exhibits higher sensitivity in lower temperature ranges.

3.4. YbGAGG: Cr³⁺ Thermometer Based on the Photoluminescence Intensity Ratio of Cr³⁺/Yb³⁺ (Mode 2)

The temperature dependence of the PL spectrum of the YbGAGG: Cr³⁺ sample, excited at 455 nm, is shown in Figure 7a. The several PL peaks in the range of 650–800 nm originate the ²E-⁴A₂ transition of Cr³⁺, and their intensity strongly decreases with increasing temperature. The integrated PL intensity of Yb³⁺ above 900 nm, as discussed in Section 3.3, increases with rising temperature (as illustrated by the red triangle plot in Figure 7b). The Boltzmann distribution and different transition probabilities between ²F_7/2-²F_5/2 with Stark levels can result in a negative thermal quenching. Additionally, the temperature dependence of energy transfer efficiency from Cr³⁺ to Yb³⁺ can play a part in this phenomenon (a demonstration of the energy transfer process can be found in the earlier discussion about Figure 3b). The opposite tendency between temperature-dependent PL intensities of Yb³⁺ and Cr³⁺ implies this hypothesis. For an efficient energy transfer, the luminescence spectrum of the donor and the absorption spectrum of the accepter should be overlapped. However, there is an energy mismatch between Cr³⁺: ²E → ⁴A₂ luminescence and Yb³⁺: ²F_7/2-²F_5/2 absorption. This energy gap can be compensated efficiently at higher temperatures by two possibilities: Cr³⁺ PL broadening and phonon assist.

As the most common explanation for the temperature quenching of rare earth luminescence centers, the intensity of the weak multi-phonon relaxation effect for Yb³⁺ depends on the relationship between the phonon cut-off energy of the host material and the energy difference between the excited state and the ground state. Although the phonon cut-off energy of the GAGG host is as high as 808 cm⁻¹ [27], the energy difference between Z_low and the ground state ²F_5/2 of Yb³⁺ exceeds 9500 cm⁻¹, depending on the intensity of the Stark split effect. In this case, the possibility of the multi-phonon relaxation process is negligible.

The shape of the PL signal of Cr³⁺ in Figure 7a is sharp peaks, which is believed to be a phenomenon that occurs when Cr³⁺ is in a strong crystal field. In GAGG, the octahedral sites are occupied by smaller Al³⁺ ions (0.535 Å) [28,29], resulting in a strong crystal field for the Cr³⁺ (0.615 Å) dopants. This results in the ²E energy level of Cr³⁺ becoming the lowest excited state, leading to the sharp peak shape of the PL spectrum.

To investigate the influence of the crystal field on the PL of Cr³⁺, Racah parameters were calculated to explore the effect of the crystal field strength on the d orbitals of Cr³⁺ and the shape of the PL spectrum. The formulas for calculating the crystal field strength (10Dq) and the Racah parameters (B and C) are as follows [30,31,32]:

$$E\left({}^{4}T_2\right)=10Dq$$

(6)

$$\frac{Dq}{B}=\frac{15(\Delta E/Dq-8)}{{(\Delta E/Dq)}^2-10(\Delta E/Dq)}$$

(7)

$$\frac{E\left({}^{2}E\right)}{B}=\frac{3.05C}{B}+7.90-\frac{1.80B}{Dq}$$

(8)

where ΔE = E(⁴T₁(⁴F)) − E(⁴T₂). E(⁴T₁(⁴F)), and E(⁴T₂) are, respectively derived from the positions of the ⁴T₁ and ⁴T₂ bands of Cr³⁺ in Figure 3a, while the value of E(²E) is derived from the position of the R-line of Cr³⁺ PL spectrum in Figure 7a (691.53 nm). The final calculations result in Dq = 1658.9 cm⁻¹, B = 631.53 cm⁻¹, and C = 3244.1 cm⁻¹. Based on the above parameters, we can derive the Tanabe−Sugano diagram (as shown in Figure 8). Under excitation by a 660 nm light source, Cr³⁺ will transition from the ⁴A₂ ground state to the ⁴T₂ state and then relax to the ²E state (as shown in Figure 9). The lowest excited state ²E and the ground state ⁴A₂ are weakly coupled [33], so the emission from ²E to ⁴A₂ does not experience strong thermal quenching due to the cross-over effect. The extremely low PL intensity of Cr³⁺ at room temperature is mainly due to the high phonon assistant energy transfer efficiency from Cr³⁺ to Yb³⁺ [34].

The luminescence intensity of Cr³⁺ decreases sharply with increasing temperature, as indicated by the blue square in Figure 7b. For Cr³⁺, as mentioned in Section 3.3, the Cr³⁺ luminescence is quenched at a higher Yb³⁺ concentration due to the efficient Cr³⁺ → Yb³⁺ energy transfer process. The opposite temperature dependence of Yb³⁺ and Cr³⁺ exhibits considerable thermometric sensitivity, especially at temperatures around 100 K.

The LIR plots shown in Figure 7c were directly obtained from the integrated intensities of Yb³⁺ and Cr³⁺ in the temperature range of 100–320 K in Figure 7b, based on the formula of $LIR=\frac{I_{{\mathrm{C}\mathrm{r}}^{3+}}}{I_{{\mathrm{Y}\mathrm{b}}^{3+}}}$ (Mode 2), where $I_{{\mathrm{C}\mathrm{r}}^{3+}}$ and $I_{{\mathrm{Y}\mathrm{b}}^{3+}}$ represent the integrated intensities of Cr³⁺ and Yb³⁺, respectively. A fitting function was employed to analyze these LIR plots further, as defined by Equation (3):

$$LIR=a_1\times exp\left(-\frac{T}{a_2}\right)+a_3{T}^2+a_{4}T+a_5$$

(9)

The calculation of the temperature dependence of S_a and S_r of the YbGAGG: Cr³⁺ thermometer based on the luminescence intensity ratio $LIR=\frac{I_{{\mathrm{C}\mathrm{r}}^{3+}}}{I_{{\mathrm{Y}\mathrm{b}}^{3+}}}$ was also conducted using the method described in Section 3.4 and shown in Figure 7d. Notably, at 100 K, S_r reaches its maximum value of 2.69% K⁻¹. This indicates a high level of sensitivity at lower temperatures for Mode 2.

4. Conclusions

The development and thorough analysis of the double-mode YbGAGG: Cr³⁺ thermometer highlights its significant potential in temperature measurement applications. Excitation and emission of Mode 1 of the YbGAGG: Cr³⁺ thermometer are within the two BTW range. By utilizing the opposite temperature dependence of the PL from different Stark sublevels of Yb³⁺, a S_r value of 0.55% K⁻¹ was achieved at 310 K. These results highlight the potential of this thermometer for biomedical temperature measurement. Additionally, Mode 2 of the YbGAGG: Cr³⁺ thermometer exhibits high sensitivity at a low-temperature range, reaching a maximum S_r of 2.69% K⁻¹ at 100 K. This is attributed to the slight possibility of the multi-phonon relaxation processes of Yb³⁺ and the intense energy transfer process from Cr³⁺ to Yb³⁺ induced by the high Yb³⁺ concentration. The unique temperature-dependent behaviors observed in the two modes of YbGAGG: Cr³⁺ offer valuable insights into the design and enhancement of luminescence thermometers, paving the way for more advanced and precise temperature measurement technologies.