1. Introduction
Figure 1 shows an example of a typical compound forming ternary system. In Sn–Pt–Pd, one compound (Pd
3Sn
2) extends deeply in the ternary field towards a metastable Pt
3Sn
2 phase; another (
L1
2) is going from one of the binary systems to the other crossing the complete composition field. Both homogeneity domains are parallel to the Pt–Pd axis. In such a case, a substitutional model can be anticipated to account for the composition changes within the homogeneity domains, justified by the similar electronic properties and atomic radii of these two latter atoms. This type of system will be called regular in the sense that, if one element is close to another element in terms of electronic properties and/or atomic radius, then, the homogeneity domains are oriented parallel to the axis defined by these two elements.
Figure 1.
Isothermal section at 1000 °C of the Sn–Pt–Pd system (redrawn from [
1], Copyright 1981, Mineralogical Association of Canada).
Figure 1.
Isothermal section at 1000 °C of the Sn–Pt–Pd system (redrawn from [
1], Copyright 1981, Mineralogical Association of Canada).
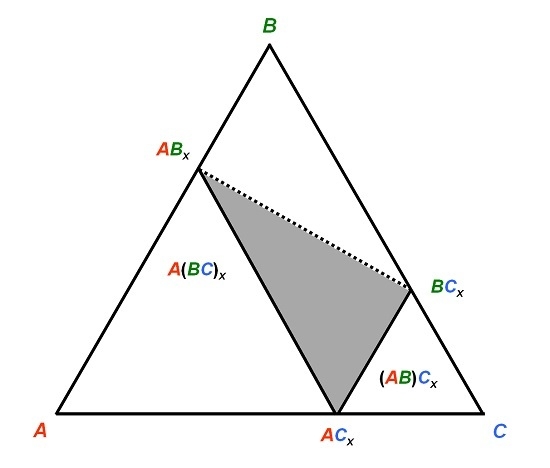
Let’s imagine now a system
A–B–C as exemplified in
Figure 2 so that
RA >
RB >
RC. A compound
ACx forms. Generally the larger atom
A would occupy the sites with higher coordination number (CN). There may be a tendency for the intermediate size
B atom to replace
C in order to form a stable (or metastable)
ABx. However, there may also be a tendency for
B to form with
C the compound
BCx. Due to its larger size,
B should then occupy the sites with high CN. If the stability of the phase is driven by geometrical reasons (the larger atom occupies the sites with high CN), then the three compounds
ACx,
ABx, and
BCx respect the size criterion. This has two distinct consequences. First, one may find rather irregular shapes of the homogeneity domain in the phase diagram, typically located within the triangle drawn in
Figure 2, since starting from
ACx,
B may have a tendency to substitute for both
A and
C. Second, one should expect a site preference reversal of the intermediate
B atom when crossing the homogeneity domain between
ABx and
BCx (dashed line in
Figure 2). This is not without consequences on the ternary phase stability.
This type of system will be called irregular for the following reasons. Though rather unusual, this phenomenon may happen in real systems. As far as we know, it has never been described in detail in previous literature. The present paper reviews the systems in which this phenomenon has been demonstrated though not yet analyzed and we tried to derive some conclusions about the occurrence of this phenomenon. To avoid confusion, all the systems will be named and the phase diagrams will be drawn respecting the order A–B–C with RA > RB > RC. Results from the literature are described but new results obtained especially on the systems Zr–Nb–Fe and Re–Cr–Co are also presented.
Figure 2.
Schematized isothermal section of a system A–B–C in which the compound ACx has a tendency to be substituted on both sites by the B atom, forming stable or metastable BCx and ABx compounds.
Figure 2.
Schematized isothermal section of a system A–B–C in which the compound ACx has a tendency to be substituted on both sites by the B atom, forming stable or metastable BCx and ABx compounds.
2. Experimental Techniques and Methodology
Three techniques are now described that can be combined to study the phenomenon described in the present paper (for more details see [
2]).
First, the study of the isothermal sections of phase diagrams is essential in order to assess the shape of the homogeneity domain. They can be collected from the literature or, when needed, one’s own determination can be made. Alloys can be synthesized by arc-melting of the pure elements followed by a convenient annealing at the required temperature and quenching. The characterization of the nature of the present phases is done by X-ray diffraction, and the composition of each phase is determined by electron probe micro-analysis (EPMA). In the present work, Re–Cr–Co alloys were obtained by arc melting of the pure elements (pellet obtained from the powders of Re and Cr, Alfa Aesar, 99.99%, and Co, Aldrich, 99.99%) followed by an annealing at 1150 °C in evacuated sealed silica tubes for six weeks. Due to difficulties in reducing the inhomogeneities related to the solidification in the Re-richer sample at this temperature, this sample was submitted to a first annealing treatment at 1500 °C under argon for 8 h in an induction furnace before the annealing at 1150 °C. The EPMA measurement was carried with a Cameca SX 100 apparatus using Kα lines for Cr and Co and Lα line for Re.
In the present study, devoted to site reversal, it is obviously of primary importance to be able to experimentally obtain the site occupancies of the three atoms on the different sites of the crystal structure as a function of composition. X-ray or neutron diffraction alone cannot be used to solve this type of problem since, from one diffraction dataset, one can obtain only one occupancy parameter per site to match the average scattering density. If one has to obtain, on each site, the two site occupancies necessary to define the structure when three elements are present together at the same position, one has to use two diffraction datasets in which the diffraction contrast is different. Ternary site occupancies can therefore be obtained in many cases by combined Rietveld refinement of neutron (ND) and X-ray (XRD) diffraction data. This is illustrated in
Figure 3 in the case of the Mo–Re–Ni system. The red lines show the locus of compositions giving the same neutron scattering density at a given site. All the site compositions on the line would give the same agreement with the diffraction data in a structure refinement if the neutron diffraction only was used. The same lines can be drawn for X-ray and it is evident that only one composition can result in a good refinement of both XRD and ND data. One may appraise how accurately the exact site composition can be determined in this particular system by the fact that the lines cross orthogonally. Note that this is not always the case and the accuracy depends on the relative values of the Fermi lengths and atomic numbers of the three present elements. In
Figure 3, the example of the Mo–Re–Cr system is also presented for which the lines are almost parallel and the determination of ternary site occupancies would be much less accurate.
Figure 3.
Diagrams showing as parallel lines the compositions of a site occupied by the three atoms Mo, Re, and Ni (A) or Cr (B), giving the same diffraction scattering density with X-rays (in blue; it is assumed that the scattering is proportional to the average Z) and neutrons (red).
Figure 3.
Diagrams showing as parallel lines the compositions of a site occupied by the three atoms Mo, Re, and Ni (A) or Cr (B), giving the same diffraction scattering density with X-rays (in blue; it is assumed that the scattering is proportional to the average Z) and neutrons (red).
This technique was used in the case of Zr–W–Re [
3], Mo–Re–Ni [
4], and Re–Cr–Co systems (this work) in order to obtain the ternary site occupancies for the χ and the σ phases. In each case the neutron diffraction measurements were performed at Laboratoire Léon Brillouin (common laboratory CEA-CNRS) in Saclay, France using the instrument 3T2. The powder sample (typically 6–8 g, <63 μm) was placed in a vanadium cylinder (diameter 6 mm) and the measurement was performed at room temperature with Debye-Scherrer geometry in the presence of five detectors. For each pattern, data were recorded in the angular range 5° ≤ 2θ ≤ 121° with a step size of 0.05° using neutrons of wavelength 1.2253 Å. The X-ray measurements were done on a Bruker D8 Advance apparatus working in the Bragg-Brentano geometry in the θ–θ mode with Cu Kα radiation and a graphite monochromator in the diffracted beam. The usual conditions for the measurements are 5–120° (2θ), step 0.04°, time per step 20–60 s.
To determine site occupancies, the combined Rietveld analysis of XRD and ND data was conducted using the FULLPROF program in the multipattern mode (joint refinement). For refinement, the background was either interpolated between the peaks or refined with a polynomial. The pseudo-Voigt function was used to define the peak shape in both XRD and ND patterns. Because Re and Co present a non-negligible absorption coefficient for neutrons, an absorption correction was also applied by calculating the values of the absorption coefficient (μ
r) for each composition. To calculate the absorption coefficient, the density of non-compacted powders was estimated to be ~40% of the density of the material. Also, micro-absorption for the flat-plate geometry of X-ray measurements was taken into account in particular in order to be able to describe both XRD and ND data with a unique structural model including unique displacement parameters. The site occupancies are refined using a composition constraint and maintaining full occupancy at each site. The way to handle such complex relations between the parameters is described in [
5].
First-principles calculation of stable and metastable intermetallic phases has become routine. However, systematic calculations in ternary systems may become rather complex. For a crystal structure with
n independent sites in the unit cell, the ordered distribution of three atoms among each site generates 3
n configurations. If the calculation is feasible for intermetallic compounds with two or three sites like C15 and C14, it gets much more complex for phases like χ and σ with four and five sites generating 3
4 = 81 and 3
5 = 243 ordered configurations. For this reason, the ZenGen code was developed, allowing us to perform systematic calculations of all the configurations generated by the distribution of the three elements among the sublattices [
6]. Above six sites, the computation time may become prohibitive due to the increase in both the number of configurations and the complexity of the structure; simplifications should be adopted, such as merging different crystallographic sites.
The presented calculations are based on the density functional theory (DFT) and were carried out using the VASP package [
7,
8]. The generalized gradient approximation (GGA) was used with the Perdew-Burke-Ernzerhof (PBE) exchange and correlation energy functional [
9,
10]. An energy cutoff of 400 eV was used for the plane wave basis set, and a dense grid of
k-points was used with the sampling generated by the Monkhorst-Pack procedure [
11]. For each ordered configuration, both the internal atomic coordinates and the lattice parameters were fully relaxed using successive steps, keeping the original cell structure. The conditions for the calculations (method, accuracy) have been detailed previously [
3,
4]. All the calculations have been handled using the ZenGen code [
6] (generation of input files, job monitoring, extraction of results).
This procedure allows the calculation of the heat of formation of every compound generated by assigning each element to each crystal site, and gives access to the stability of the phase. At a finite temperature, the Gibbs energy is treated in the framework of the Calphad approach using the Compound Energy Formalism [
12] in the Bragg-Williams-Gorsky approximation,
i.e., considering only the configurational entropy and neglecting the entropy from atomic correlations and excess interaction parameters within the same sublattice. The procedure is described in [
13]. Not only can the stability be obtained from the calculations in this approach but also the site occupancies as a function of composition and temperature. All the thermodynamic calculations are done with Thermo-Calc software.
New calculations have been carried out in the present paper, corresponding to the study of the Laves phases in Zr–Nb–Fe system and the σ phase in Re–Cr–Co systems.
4. Discussion
In an A–B–C system in which B has an intermediate size between A (larger atom) and C (smaller atom), there may exist a tendency to form the same ordered phase in the three constituting binary systems. This may cause irregular, somewhat triangular, shapes of homogeneity domains in isothermal sections. If the atom ordering obeys geometrical criterion, then the fact that B is smaller than A but larger than C causes a reversal of the ordering. When crossing the homogeneity domain, the B atom has to switch from the site it occupies when associated with A atoms to the other sites when associated with C. Note that what is said about size and geometrical factors determining the site occupancies could be easily transposed to valence or electronic properties.
We have shown that this behavior is not pure speculation but actually exists in a number of ternary systems. Of course, the three compounds do not necessarily exist as stable phases but the important point is that they are sufficiently close to stability to produce extensive homogeneity domains pointing in their direction. We have shown examples in which two compounds (ACx and BCx: Zr–Nb–Fe, Zr–W–Re; ABx and BCx: Mo–Re–Cr, Re–Cr–Co) or one compound (ABx: Cr–Mn–Si, Mo–Re–Ni) only was stable. Calculations could be made in any system for any type of phase but are worthwhile only if an odd homogeneity domain (or known inverse atomic distribution in the binaries, like in the Mo–Re–Cr and Re–Cr–Co systems) points to the possible existence of site reversal.
We made a systematic scan of the Handbook of Ternary Alloys Phase Diagrams [
29] to check for the occurrence of irregular homogeneity domains. The systems presented in this review are the only ones, to our knowledge, for which a detailed structural study of site reversal has been documented. Another interesting phase is the γ brass structure that has irregular homogeneity domains in many systems (e.g., Cd–Cu–Sn or Cu–Pt–Zn) but no detailed structural work showing that site reversal exists.
Let us examine in which systems this phenomenon may be observed. These systems must differ strongly from the systems in which one observes a simple substitution (generally observed when two elements are similar and one is different from the two others) or no substitution at all (the three elements are very different). There should be a similar difference of radius/electronegativity between A and B and between B and C and the three compounds ABx, ACx, and BCx should exist or be close to stability in the binary systems. This would exclude in principle the phases for which a strongly covalent bonding is involved or the bonding is metallic but very localized (systems with transition metals and rare earths). The irregular systems are therefore mainly systems associating three transition metals.
We have presented only phases pertaining to the group of the topologically close-packed (TCP) phases. It seems that this type of structure favors this phenomenon. First, because the bonding has to be mainly metallic, second because transition metal systems are favored because they offer along the transition series wide and smooth variations of atomic radius and electronegativity. Finally, because there are not so many intermetallic phases in transition metal systems that are not TCP. Other phases are ordered structures from the bcc, hcp, or fcc solid solutions. See, for example, the bow-shaped homogeneity domain of the B2 phase in the Al–Pd–Sc or Al–Ru–Sc systems. However, for B2 or L10, for example, there is no reversal since the two sites in the crystal structure are symmetrically equivalent.
For other ordered phases like L12, the situation is more complex. Note that the site reversal exists already in several binary systems like Au–Cu (L12 exists at both compositions AuCu3 and Au3Cu and crystallizes in two anti-structures). However, we could not find any ternary system showing reversal in a continuous manner. The reason is the presence of other ordered structures like ternary L21 for example or other intermetallic phases. Extensive homogeneity domains are not favored because of the low temperatures necessary to have ordered phases.
The TCP phases are known to have broad ranges of homogeneity and may be highly non-stoichiometric therefore offering certain structural flexibility. Their stability and site occupancies are more influenced by geometry and atomic sizes than the electronic properties of constituting atoms. They are therefore prone to show these irregular homogeneity domains caused by the geometric accommodation of three atoms of different sizes. The fact that, in these phases, the atomic radius monitors the site occupancies according to the site CN also favors this behavior. It also seems to be important to have ternary configurations stabilizing the phase (χ phase in Zr–W–Re, C14 phase in Zr–Nb–Fe). This is also typical of the TCP phases with their often complex structures.
Then, one may wonder why rhenium appears in most of the systems presented here. It is because rhenium has an intermediate size and intermediate electronic properties (half-filled d-band). Therefore, it forms many compounds (it is the element involved in the largest number of binary σ and χ phases) and it may be larger or smaller than the other element (Re is the large atom in Re–Cr–Co, the medium one in Mo–Re–Ni, and the small one in Zr–W–Re).
The
B atom, through switching its preference from low CN sites to high CN sites, reaches a state in which it is completely disordered. In the middle of the dotted line in
Figure 2, one reaches the composition (
A0.5B0.5)(
B0.5C0.5)
x. The configurational entropy for this composition is equal to that of a binary disordered solid solution (−0.69 in unit of
R)
i.e., not very far from a completely disordered ternary solid solution (−1.10 in unit of
R), so that one could expect a stabilization of this state at high temperatures due to entropic effects. By reference to high entropy alloys [
30], we could propose the concept of high entropy intermetallic compounds.
On the other hand, the site reversal should cause miscibility gaps inside the phase at low temperatures. A simple substitution can occur at low temperatures if ideal or with a negative enthalpy of mixing. This is not the case if one goes from
ABx to
BCx because the replacement cannot be done in one step and involves site reversal. This causes miscibility gaps, shown by phase diagram calculations at low temperatures from the DFT data (see, for example, the σ phase diagram of the Mo–Re–Cr system calculated at low temperature in [
22]). Experimentally, the miscibility gap between the two
C14 phases is clearly shown in the Zr–Nb–Fe system (see
Figure 5) and also confirmed by the calculation.