A Chaotic Secure Communication System Design Based on Iterative Learning Control Theory

Abstract

This paper presents an application of Iterative Learning Control (ILC) theory to secure communication system design by using chaotic signals, where the logistic-map is employed as a source of chaos. Meanwhile, the ILC scheme is employed as a tool to encrypt and decrypt a message. A set of numerical experiments is realized to evidence the performance of our system, including the noisy case on the channels of communication of the proposed scheme.

1. Introduction

Iterative Learning Control theory (ILC; the staple of ILC can be found in a U.S. patent filled in 1967 and available in 1971 [1]) is basically a control strategy to improve transient response (or similarly, the controller performance) of dynamical systems that operate repetitively (also called multi-pass or repetitive dynamic processes). This is done by adjusting the system control input(s) during the system cycle operations [1,2,3,4]. Because the system executes the same task multiple times, the control law may learn from the previous system action (or iteration). Hence, the central challenger of ILC design is to use this information from the previous operation to learn and improve the controller execution over the next iteration by following a control objective. Basically, a repetitive dynamic system is a process that has the following two properties:

• Repetitive action, and
• Iteration.

The first one is the process action that it is periodically repeated, and the second one is the natural iteration between the plant vector state and the repetitive process action.

On the other hand, ILC control strategy has been widely employed in many industrial applications, including manufacturing, robotics, chemical process, among many others [1]. Furthermore, the main benefits of iterative learning control framework are its low transient tracking error, despite large model uncertainty and disturbances [1,5,6], its short a priori knowledge about the system to be controlled, and its low computational effort for control realization [7].

To note, ILC theory has also been used in system modeling, two-dimensional systems analysis, linear matrix inequality system design, and in adaptive and robust control innovation (see, for instance, [5,6] and references therein). In the meantime, some other ILC strategies are mainly based on Lyapunov’s theory [8,9,10].

Finally, many of the available ILC approaches require identical resetting initial conditions (at the beginning of each iteration: the well known resetting condition); however, in real applications, the perfect resetting condition may be not realizable [6,8]. Therefore, under different tests on resetting initial conditions, the boundedness along the time evolution and asymptotic stability on each iteration of an ILC system were well proven in [8]. Actually, this is an important robust property of the ILC tool to design new engineering developments, such as secure communication systems subject to noisy environments.

In this paper, motivated by the canonical ILC structure stated in [8], a chaotic secure communication scheme is developed. This design is based on the chaotic logistic-map. Therefore, the proposed design uses the ILC method as a base tool to encrypt and decrypt a message, recalling that the development of new chaotic secure communication systems is still an important open topic [11,12,13,14,15].

The remainder of this paper is organized as follows. In Section 2, the canonical ILC frame is retrieved from [8]. Section 3 presents our ILC chaotic secure communication system design. Performance numerical evaluation of our scheme is evidenced in Section 4. Finally, the conclusions are given in Section 5, including future issues on the subject.

2. The Canonical ILC System

Let us consider the next first-order nonlinear system in the i-th iteration [8]:

$${\dot{x}}_i=\theta \left(t\right)\xi (x_i,t)+u_i,t\in [0,T],x\left(0\right)=x_0,$$

(1)

where $\xi (x_i,t)(={\xi }_i\mathrm{for} \mathrm{simplicity})$ is a known nonlinear function which can be locally Lipschitz, $\theta \left(t\right)\in C[0,T]$ is the unknown time-varying parameter, and T represents the iteration (or operation) time.

Given the reference trajectory supplied by:

$${\dot{x}}_r=f(x_r,r,t),$$

(2)

where $f_r=f(x_r,r,t)$ is a known smooth-function and r is a reference input signal which produces a bounded response $x_r\left(t\right)$ over the time interval $[0,T]$, the ILC objective is to find a sequence of appropriate control inputs $u_i$ for $t\in [0,T]$ such that the system state $x_i$ tracks (as well as possible) the reference trajectory $x_r$ as $i\to \infty$ [8].

A solution to the ILC objective is as follows [8]:

$$\begin{array}{ccc}\hfill u_i& =& k{e}_i+f_r-{\widehat{\theta }}_i\left(t\right){\xi }_i,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill {\widehat{\theta }}_i\left(t\right)& =& \mathrm{proj}({\widehat{\theta }}_{i-1}\left(t\right))-{\xi }_i{e}_i,{\widehat{\theta }}_{-1}\left(t\right)=0,\hfill \end{array}$$

(4)

where $e_i=e_i\left(t\right)=x_r\left(t\right)-x_i\left(t\right)$,

$$\mathrm{proj}\left(x\right)=\left\{\begin{array}{cc}x,\hfill & \mid x\mid \le {\theta }^{*}\hfill \\ \mathrm{sign}\left(x\right){\theta }^{*},\hfill & \mathrm{otherwise}\hfill \end{array}\right.;$$

(5)

and ${\theta }^{*}$ is the parameter projection bound, assumed sufficiently large. According to [8], this ILC—even under random and bounded initial conditions $e_i\left(0\right)$ (if $e_i\left(0\right)=0$ implies ideal resetting condition.)—assures the ILC control objective. Finally, the learning parameter ${\widehat{\theta }}_i\left(t\right)$ gives an estimation of the time-varying parameter $\theta \left(t\right)$ over each iteration of the repetitive process.

3. Chaotic Secure Communication Design Based on ILC Theory

This section presents our secure communication system design by employing the chaotic logistic-map and by using the ILC framework as a tool to encrypt and decrypt a message. We are going to use its property for the estimation of the unknown time-varying parameter $\theta \left(t\right)$.

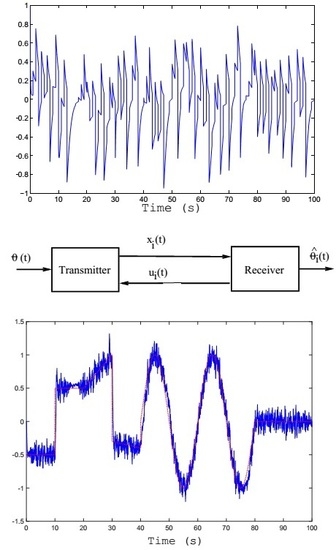
To begin with, let us refer to the main block diagram shown in Figure 1. Allow us to define the transmitter block as:

$$\dot{x_i}=\theta \left(t\right){\xi }_i+u_i,x_i\left(0\right)=x_{i-1}\left(T\right).$$

(6)

The initial conditions $x_i\left(0\right)=x_{i-1}\left(T\right)$ means that the end state of the preceding iteration becomes the initial state for the new one. Here, $\theta \left(t\right)$ represents the message to be encrypted. In our design, we are using a two-channel communication system. The transmitted signal $x_i\left(t\right)$ goes on one channel, and on the other travels the generated signal $u_i\left(t\right)$ coming from the receiver (see Figure 1). Both signals have to be in random-like behavior with the message encrypted in $x_i\left(t\right)$. Then, ${\widehat{\theta }}_i\left(t\right)$ becomes the decrypted signal (an estimation of the transmitted message in $\theta \left(t\right)$). To complete our design for the transmitter section, let us define ${\xi }_i=x_i(1-x_i)$, a mimic expression from the chaotic logistic-map.

Now, designing the receiver block as:

$$\begin{array}{ccc}\hfill {\dot{x}}_r& =& -x_r+z\left(j\right),x_r\left(0\right)=0.1,\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\widehat{\theta }}_i\left(t\right)& =& \mathrm{proj}({\widehat{\theta }}_{i-1}\left(t\right))-{\xi }_i{e}_i,{\widehat{\theta }}_{-1}=0,\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill e_i\left(t\right)& =& x_r\left(t\right)-x_i\left(t\right),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill u_i\left(t\right)& =& k{e}_i\left(t\right)+f_r-{\widehat{\theta }}_i\left(t\right){\xi }_i,\hfill \end{array}$$

(10)

where $z\left(j\right)$ is realized by employing the well-known discrete-time chaotic logistic-system:

$$z(j+1)=4z\left(j\right)(1-z(j\left)\right),z\left(0\right)=0.1(\mathrm{we}\mathrm{set}z\left(0\right)=x_r\left(0\right),\mathrm{but}\mathrm{it}\mathrm{does}\mathrm{not}\mathrm{matter}),j=0,1,2,3,\cdots .$$

(11)

The output of the logistic-map $z\left(j\right)$ (utilized as the reference signal $r=r\left(t\right)$ to $f_r$) is assumed being performed having a zero-order-holder device (ZOH), T being the time duration between discrete-time samples. Recall that the ZOH device is a transformation mechanism to translate a discrete-time signal to a piece-wise continuous-time one (see, for instance, Chapter 1 in [16]).

Stability issue—The stability issue of the overall closed-loop communication system is warranted by the results given in [9] and stated in Section 2, including its robustness property.

4. Numerical Experiments

To display numerical experiment results, let us complete our secure communication design by using $T=1$ s, ${\theta }^{*}=10$ Rad, and $k=10$, and again, ${\xi }_i=x_i(1-x_i)$. The test message used as $\theta \left(t\right)$ and the obtained estimation of the message $\widehat{{\theta }_i}\left(t\right)$ at the receiver part are shown in Figure 2. Figure 3 shows $x_r\left(t\right)$ and $x_i\left(t\right)$. We can appreciate a random-like behavior on these, due to the chaotic logistic-map employed in our system. Because they are too similar, Figure 4 displays a zoomed-in version of the error dynamic. The signal $u_i\left(t\right)$ is pictured in Figure 5. Finally, Figure 6 illustrates the numerical results when random noises are presented on each channel of the communication system, where we insert uncorrelated normal distribution noises with zero mean and standard deviation of $0.05$. For comparison, Figure 7 displays the error dynamic for the noisy case. From this, we can note that the external noise helps, in some way, to better hide our secret message.

5. Conclusions

This paper has described an application of the ILC theory to secure communication system design by using a chaotic signal obtained from the chaotic-logistic map. It was also evidenced that the main important benefit of the proposed ILC given in [8] is robustness, even on variation in the resetting initial conditions and exogenous noise. From our secure communication system, an important design parameter is the T-time duration of each cycle. By reducing it, we may be able to employ our system to more “faster-time” message signals. It is worth mentioning that the ILC method belongs to the data-driven systems, due to data measurement used in its learning algorithm [17].

Finally, we believe that it is important to highlight that the main aim of this paper is to illustrate a kind of academic example of an application of the ILC theory to secure communication system design based on chaotic signals. However, and because it is beyond the author’s expertise, an additional analysis test is missing; for instance, the bit error rate curve over AWGN (Additive White Gaussian Noise) channel, including the possibility to expand our design by using the latest works on chaotic waveform to convey data such as DCSK (Differential Chaos Shift Keying), NR-DCSK (Noise Reduction Differential Chaos Shift Keying), and so on. All of these are left for a future work.