Maximum Efficiency per Torque Control of Permanent-Magnet Synchronous Machines

Abstract

High-efficiency permanent-magnet synchronous machine (PMSM) drive systems need not only optimally designed motors but also efficiency-oriented control strategies. However, the existing control strategies only focus on partial loss optimization. This paper proposes a novel analytic loss model of PMSM in either sine-wave pulse-width modulation (SPWM) or space vector pulse width modulation (SVPWM) which can take into account both the fundamental loss and harmonic loss. The fundamental loss is divided into fundamental copper loss and fundamental iron loss which is estimated by the average flux density in the stator tooth and yoke. In addition, the harmonic loss is obtained from the Bertotti iron loss formula by the harmonic voltages of the three-phase inverter in either SPWM or SVPWM which are calculated by double Fourier integral analysis. Based on the analytic loss model, this paper proposes a maximum efficiency per torque (MEPT) control strategy which can minimize the electromagnetic loss of PMSM in the whole operation range. As the loss model of PMSM is too complicated to obtain the analytical solution of optimal loss, a golden section method is applied to achieve the optimal operation point accurately, which can make PMSM work at maximum efficiency. The optimized results between SPWM and SVPWM show that the MEPT in SVPWM has a better effect on the optimization performance. Both the theory analysis and experiment results show that the MEPT control can significantly improve the efficiency performance of the PMSM in each operation condition with a satisfied dynamic performance.

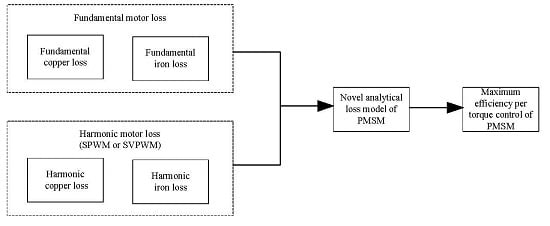
1. Introduction

Compared with direct-current (DC) motors and induction motors, permanent magnet synchronous motors (PMSMs) are preferred to power propulsion in the aviation and aerospace field for their high efficiency and high power-to-weight ratio. The efficiency performance is particularly important in the aviation and aerospace field since there is only limited energy. The efficiency of PMSMs will directly be related to the safe run time, battery size and effective load capacity.

The motor losses of PMSMs consist of mechanical loss, copper loss, iron loss and stray loss. To achieve a higher efficiency of PMSMs, the electromagnetic structure is in the optimized design to reduce the copper loss and iron loss [1,2,3]. However, the high-performance PMSMs need not only the optimal design of the electromagnetic structure but also efficiency optimization control strategies. There are several vector control strategies for PMSMs such as i_d = 0 control, unity power factor (UPF) control, maximum torque per ampere (MTPA) control, maximum speed per voltage (MSPV) control and loss model control (LMC). The i_d = 0 control keeps the electromagnetic torque and q-axis current in a linear relationship by keeping the d-axis current at zero [4,5]. The i_d = 0 control is widely used in surface-mounted PMSMs (SPMSMs) and will not damage the permanent magnet. The i_d = 0 control is the MTPA control in SPMSMs as the inductance in the d-axis is equal to that in the q-axis, and the torque is linearly related to the q-axis current. However, i_d = 0 control cannot maximize the electromagnetic torque in interior PMSMs (IPMSMs), and, therefore, MTPA control is presented to make the most use of the reluctance torque in IPMSMs [6,7]. The MTPA control can achieve the minimum copper loss since the least armature current is required to obtain the same electromagnetic torque. The i_d = 0 control and MTPA control only optimize the copper loss and will not raise the maximum efficiency of PMSMs [8,9,10]. The MSPV control can minimize the winding terminal voltage and significantly decrease the iron loss. The MSPV control just affects the iron loss and cannot acquire the minimum loss of the PMSM. The UPF control could decrease the reactive power to zero and reduce the energy loss between power transmissions [11,12]. However, the UPF control does not focus on the loss of the PMSM and will not achieve the maximum efficiency in each operation condition of the PMSM. The LMC takes into account both the copper loss and iron loss of the PMSM, and could optimize the motor loss in the whole operation range of the PMSM [13,14]. However, the LMC only focuses on the optimization of the fundamental loss of the PMSM and ignores the harmonic loss of the PMSM. As the PMSM is fed by the pulse-width modulation (PWM) inverter, there must be a large number of harmonic components on the terminal voltage of the PMSM. The harmonic voltage will cause the harmonic current in the PMSM which can generate harmonic loss and have an influence on the efficiency of the PMSM. To acquire the minimum motor loss, the efficiency optimization control algorithm has to consider both the fundamental loss and harmonic loss.

This paper proposes a novel analytic loss model of PMSMs, which is able to calculate fundamental loss (copper loss and iron loss) and harmonic loss (iron loss) together in either sine-wave pulse-width modulation (SPWM) or space vector pulse width modulation (SVPWM). The fundamental iron loss is estimated by the average flux density in the stator tooth and yoke. As the PMSM is fed by the PWM inverter, the harmonic content of the output voltage in the inverter is analyzed by the double Fourier integral analysis and the harmonic loss is obtained in the Bertotti iron loss formula by the harmonic voltages. Based on the entire frequency domain loss model, this paper proposes an efficiency optimization control strategy named maximum efficiency per torque (MEPT) control which allows optimizing both the fundamental loss and harmonic loss through the injection of the optimal direct-axis current according to the operating speed and the load conditions. In particular, a golden section method is used in order to acquire, in a fast and simple way, the optimal solution which is suitable for all kinds of PMSMs. The MEPT control is designed to improve the efficiency of PMSMs in the steady-state condition, which is the major opportunity for energy savings. The theoretical analysis and experimental tests on a specific PMSM drive employing the proposed MEPT control have shown that the efficiency performance is enhanced in each operation condition and the dynamic performance is maintained in comparison to the PMSM drive equipped with a traditional i_d = 0 control.

2. Fundamental Loss Model of PMSMs

To optimize the efficiency of PMSMs, it is crucial to build an accurate and fast approach for motor loss calculation. The controlled electromagnetic loss of PMSMs can be divided into two parts: fundamental loss and harmonic loss. The fundamental loss consists of fundamental copper loss caused by the fundamental current in the stator armature windings and fundamental iron loss caused by fundamental flux linkages in the stator and rotor. Compared with the stator iron loss, the rotor iron loss at steady state is quite small and can be neglected. So the fundamental loss model of PMSMs in this paper only takes into account the stator armature copper loss and stator iron loss.

2.1. Fundamental Copper Loss

The mathematics model of the PMSM decoupled into the d-axis and q-axis is shown in Figure 1 [15,16,17].

From Figure 1, the voltage equation of the PMSM can be described as

$$\{\begin{array}{c}{u}_d=L_{d1}\frac{d{i}_d}{dt}+R_s{i}_d+L_{dm}\frac{d{i}_{dm}}{dt}-n_p{\mathsf{\omega }}_r{\mathsf{\psi }}_q\\ u_q=L_{q1}\frac{d{i}_q}{dt}+R_s{i}_q+L_{qm}\frac{d{i}_{qm}}{dt}+n_p{\mathsf{\omega }}_r{\mathsf{\psi }}_d\end{array}$$

(1)

where L_d1 and L_q1 are the stator’s leakage inductance in the d-axis and q-axis, and L_dm and L_qm are the stator’s self-inductance in the d-axis and q-axis, respectively; R_s is the stator’s resistance, and n_p is the pole pairs of the PMSM; ω_r is the motor rotation speed; u_d,q and i_d,q are the stator’s voltage and the stator’s current, respectively; i_dm and i_qm are the magnetizing currents of the PMSM in d-axis and q-axis; Ψd and Ψq are the flux linkage in d-axis and q-axis.

The flux linkage in the d-axis and q-axis can be described as

$$\{\begin{array}{c}{\mathsf{\psi }}_d={\mathsf{\psi }}_f+L_{dm}{i}_{dm}\\ {\mathsf{\psi }}_q=L_{qm}{i}_{qm}\end{array}$$

(2)

where Ψ_f is the flux linkage of the permanent magnet.

Additionally, the current equations of the PMSM in Figure 1 are expressed as

$$\{\begin{array}{c}{i}_{di}=\frac{1}{R_i}\left(L_{dm}\frac{d{i}_{dm}}{dt}-n_p{\mathsf{\omega }}_r{\mathsf{\psi }}_q\right)\\ i_d=i_{dm}+i_{di}\end{array}$$

(3)

$$\{\begin{array}{c}{i}_{qi}=\frac{1}{R_i}\left(L_{qm}\frac{d{i}_{qm}}{dt}+n_p{\mathsf{\omega }}_r{\mathsf{\psi }}_d\right)\\ i_q=i_{qm}+i_{qi}\end{array}$$

(4)

where i_di and i_qi are the iron loss current in the d-axis and q-axis. Ri is the iron loss resistance of the PMSM.

From Equation (2), the fundamental copper loss of the PMSM can be obtained as

$$P_{f\_Cu}=\frac{3}{2}{R}_s\left(i_d^2+i_q^2\right)$$

(5)

where P_{f_Cu} is the fundamental copper loss of the PMSM. As the d-axis current i_d and q-axis current i_q are calculated by the CLARKE transmission and PARK transmission using the principle in which the flux value remains invariable, there is the transformation coefficient of $\frac{3}{2}$ in the power calculation.

The electromagnetic torque of the PMSM is described as

$$T_e=\frac{3}{2}{n}_p\left[{\mathsf{\psi }}_f{i}_{qm}+\left(L_{dm}-L_{qm}\right)i_{dm}{i}_{qm}\right]$$

(6)

The fundamental copper loss can be derived from Equation (5) as

$$\begin{array}{cc}{P}_{Cu\_f}& =\frac{3}{2}{R}_s(i_d^2+i_q^2)\hfill \\ & =\frac{3}{2}{R}_s\left\{{\left(i_{dm}+\frac{L_{dm}\frac{d{i}_{dm}}{dt}-n_p{\mathsf{\omega }}_r{L}_{qm}{i}_{qm}}{R_i}\right)}^2+{\left[i_{qm}+\frac{L_{qm}\frac{d{i}_{qm}}{dt}+n_p{\mathsf{\omega }}_r\left({\mathsf{\psi }}_f+L_{dm}{i}_{dm}\right)}{R_i}\right]}^2\right\}\hfill \end{array}$$

(7)

From the electromagnetic torque of the PMSM, the fundamental copper loss in the steady state can be simplified as

$$\begin{array}{cc}{P}_{Cu\_f}& =\frac{3}{2}{R}_s(i_d^2+i_q^2)\hfill \\ & =\frac{3}{2}{R}_s\left\{\begin{array}{l}{\left(i_{dm}+\frac{-n_p{\mathsf{\omega }}_r{L}_{qm}}{R_i}\cdot \frac{2T_e}{3n_p{\mathsf{\omega }}_f+3n_p\left(L_{md}-L_{qm}\right)i_{dm}}\right)}^2+\\ {\left[\frac{2T_e}{3n_p{\mathsf{\omega }}_f+3n_p\left(L_{md}-L_{qm}\right)i_{dm}}+\frac{n_p{\mathsf{\omega }}_r\left({\mathsf{\psi }}_f+L_{dm}{i}_{dm}\right)}{R_i}\right]}^2\end{array}\right\}\hfill \\ & =f\left(i_{dm},T_e\right)=f\left(i_d,T_e\right)\hfill \end{array}$$

(8)

From Equation (8), the fundamental copper loss is a function of the d-axis current and electromagnetic torque.

2.2. Fundamental Iron Loss

In the PMSM, the iron loss can be accurately calculated by finite element analysis (FEA) which can estimate both the fundamental iron loss and harmonic iron loss. Unfortunately, FEA is too time-consuming to be practical for efficiency optimization control. This paper presents an accurate and fast approach for iron loss calculation.

The Bertotti iron loss formula [18] is the most common evaluation method of iron loss, which calculates the iron loss per volume as

$$d{P}_{Fe}=k_h{B}_m^{2}f+\frac{{\mathsf{\pi }}^2\mathsf{\sigma }{k}_d^2}{6}{B}_m^2{f}^2+k_e{B}_m^{1.5}{f}^{1.5}$$

(9)

where k_h and k_e are the coefficients of the hysteresis loss and excess loss, respectively; σ is the conductivity of the material; and k_d is the thickness of the lamination. These four parameters are material characteristics of the motor cores; f is the frequency, and B_m is the peak value of the magnetic flux density.

To calculate the iron loss in the stator core, it is crucial to determine the accurate average flux density in the stator tooth and stator yoke, which is shown in Figure 2.

The S_t and S_y are the cross-section area of the stator tooth and stator yoke in Figure 2, respectively. Therefore, the average flux density in the stator tooth and stator yoke in the d-axis and q-axis can be obtained as

$$\{\begin{array}{c}{B}_{td}=\frac{2n_p{\mathrm{\Phi }}_d}{{\mathsf{\alpha }}_i{S}_{t}Q}\\ B_{tq}=\frac{2n_p{\mathrm{\Phi }}_q}{{\mathsf{\alpha }}_i{S}_{t}Q}\\ B_{yd}=\frac{{\mathrm{\Phi }}_d}{2S_y}\\ B_{yq}=\frac{{\mathrm{\Phi }}_q}{2S_y}\end{array}$$

(10)

where Φ_d and Φ_q are the flux in the d-axis and q-axis, α_i is the pole arc factor, and Q is the number of slots.

The d-axis and q-axis fluxes can be derived from the flux linkage as

$$\{\begin{array}{c}{\mathrm{\Phi }}_d=\frac{{\mathsf{\psi }}_d}{N_1{K}_{dq1}}\\ {\mathrm{\Phi }}_q=\frac{{\mathsf{\psi }}_q}{N_1{K}_{dq1}}\end{array}$$

(11)

where N₁ is the number of turns per phase, and K_dp1 is the fundamental winding factor. Therefore, from Equations (9)–(11), the iron loss caused by the d-axis and q-axis flux linkages or currents can be calculated as

$$\begin{array}{cc}{P}_{Fe\_f}& =d{P}_{Fetd,q}{V}_t+d{P}_{Feyd,q}{V}_y\hfill \\ & =\frac{3}{2}{k}_{hd}\left({\mathsf{\psi }}_d^2+{\mathsf{\psi }}_q^2\right)+\frac{3}{2}{k}_{ep}\left({\mathsf{\psi }}_d^2+{\mathsf{\psi }}_q^2\right)\hfill \\ & =\frac{3}{2}{k}_{hd}\left[{\left(L_{dm}{i}_{dm}+{\mathsf{\psi }}_f\right)}^2+{\left(L_{qm}{i}_{qm}\right)}^2\right]+\frac{3}{2}{k}_{ep}\left[{\left(L_{dm}{i}_{dm}+{\mathsf{\psi }}_f\right)}^{1.5}+{\left(L_{qm}{i}_{qm}\right)}^{1.5}\right]\hfill \end{array}$$

(12)

where P_Fetd,q is the fundamental iron loss of the stator tooth in the d-axis and q-axis, and P_Feyd,q is the fundamental iron loss of the stator yoke in the d-axis and q-axis. V_t and V_y are the total volumes of the stator tooth and yoke, respectively,

$$\{\begin{array}{c}{V}_t=Q{h}_t{S}_t\\ V_y=\mathsf{\pi }(D_1-h_y)S_y\end{array}$$

(13)

where h_t and h_y are the heights of the stator tooth and stator yoke, respectively. D₁ is the outer diameter of the stator.

Further, k_hd is the coefficient of the equivalent iron hysteresis and eddy losses, and k_ep is the coefficient of the equivalent iron excess loss, i.e.,

$$\{\begin{array}{c}{k}_{hd}=\left(k_h{f}_0+\frac{{\mathsf{\pi }}^2\mathsf{\sigma }{k}_d^2}{6}{f}_0^2\right)\left[\frac{{\left(2n_p\right)}^2{V}_t}{{\left({\mathsf{\alpha }}_i{S}_{t}Q\right)}^2}+\frac{V_y}{{\left(2S_y\right)}^2}\right]\\ k_{ep}=k_e{B}_m^{1.5}{f}_0^{1.5}\left[\frac{{\left(2n_p\right)}^{1.5}{V}_t}{{\left({\mathsf{\alpha }}_i{S}_{t}Q\right)}^{1.5}}+\frac{V_y}{{\left(2S_y\right)}^{1.5}}\right]\end{array}$$

(14)

where f₀ is the frequency of the stator fundamental current.

Equation (12) shows that the fundamental iron loss is a function of the fundamental frequency f₀, the d-axis current i_d and the q-axis current i_q. The increasing q-axis current, which enlarges ψ_q, will increase the iron loss, and the negative d-axis current, which can weaken the flux and reduce ψ_d, will decrease the iron loss.

The fundamental current frequency can be obtained from the rotational speed as

$$f_0=2\mathsf{\pi }{n}_p{\mathsf{\omega }}_r$$

(15)

By substituting Equations (6) and (15) into Equation (12), the fundamental iron loss is a function of the rotational speed, the d-axis current and the q-axis current.

$$P_{Fe\_f}=f({\mathsf{\omega }}_r,i_{dm},i_{qm})$$

(16)

2.3. Fundamental Loss Model

From fundamental copper loss (Equation (8)) and fundamental iron loss (Equation (12)), the fundamental loss of the PMSM can be derived as

$$P_{loss\_f}=P_{Cu\_f}+P_{Fe\_f}=f({\mathsf{\omega }}_r,i_d,i_q)$$

(17)

Equation (13) shows that the fundamental loss of the PMSM is only a function of the rotational speed ω_r, the d-axis current i_d and the q-axis current i_q. This proposed fundamental loss calculation method is verified by finite element analysis (FEA) based on a 5 kW PMSM. The FEA model is shown in Figure 3.

Based on the FEA, the analytical results of the motor fundamental loss compared with the simulation results of the FEA at different speeds and torques are illustrated in Figure 4. Additionally, the difference of the motor loss calculated by the FEA method and the proposed analytical method is shown in Figure 5.

Figure 4 shows that the fundamental loss of the PMSM in the proposed analytical method could match well with the simulation results of the FEA, and Figure 5 shows that the loss calculation error at the rated operation point where the rated speed is 2000 rpm and the rated torque is 19.1 N·m stays within 4.2%. The proposed loss calculation method can be used in the motor loss optimization.

3. Harmonic Loss Model of the PMSM

As the PMSM is fed by a PWM inverter, there must be several harmonic currents in the stator windings caused by the PWM output voltage of the inverter. The harmonic current will generate the harmonic iron loss in the stator core, which must affect the efficiency of the PMSM. To achieve the maximum efficiency of the PMSM, it is important to build an accurate harmonic loss model of the PMSM fed by a three-phase half-bridge inverter. Figure 6 shows the typical three-phase PMSM power system where 2U_dc is the DC bus voltage.

Although there are a large number of pulse-width modulation modes, SPWM and SVPWM are the most common modulation modes. Therefore, this paper only focuses on the harmonic voltage components caused by SPWM and SVPWM in the PMSM. Determination of the harmonic frequency components of a PWM switched inverter output is quite complex and is often done by using a fast Fourier transform (FFT) analysis of a simulated time-varying switched waveform. This approach could offer the benefits of expediency and reduce the mathematical effort, but it requires considerable computing capacity and always leaves uncertainty as to whether a subtle simulation round-off or error may have slightly tarnished the results obtained. In contrast, an analytical solution using double Fourier integral analysis can exactly identify the harmonic components of a PWM waveform, which ensures the correct harmonics are precise. In double Fourier integral analysis theory, the PWM output voltage of the inverter can be obtained by two time variables, x(t) and y(t), where x(t) is the carrier signal and y(t) is the fundamental (sinusoid) signal.

$$x(t)={\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c$$

(18)

where ω_c is the carrier angular frequency and θ_c is the arbitrary phase offset angle for the carrier waveform.

$$y(t)={\mathsf{\omega }}_{0}t+{\mathsf{\theta }}_0$$

(19)

where ω₀ is the fundamental angular frequency and θ₀ is the arbitrary phase offset angle for the fundamental waveform.

The output voltage of the inverter leg can be present as

$$a_n(t)=f(x(t),y(t))=\{\begin{array}{ll}2U_d{}_c& y(t)>x(t)\\ 0& y(t)\le x(t)\end{array}$$

(20)

where 2U_dc is the DC voltage, which is shown in Figure 5. The output voltage of the inverter leg is defined with respect to the negative DC bus rather than with respect to the midpoint of the DC bus, which could simplify the mathematics of the Fourier solution at the trivial expense of introducing a DC offset of +U_dc into the final solution.

With double Fourier integral analysis theory [19], the time-varying function f(x(t),y(t)) can be expressed as a summation of the harmonic components

$$\begin{array}{cc}f(x,y)& =\frac{A_{00}}{2}+{\displaystyle \sum _{n=1}^{\infty }\left\{A_{0n}\cos \left[n\left({\mathsf{\omega }}_{0}t+{\mathsf{\theta }}_0\right)\right]+B_{0n}\sin \left[n\left({\mathsf{\omega }}_{0}t+{\mathsf{\theta }}_0\right)\right]\right\}}\hfill \\ & +{\displaystyle \sum _{m=1}^{\infty }\left\{A_{m0}\cos \left[m\left({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c\right)\right]+B_{m0}\sin \left[m\left({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c\right)\right]\right\}}\hfill \\ & +{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}n=-\infty \\ (n\ne 0)\end{array}}^{\infty }\left\{\begin{array}{l}{A}_{mn}\cos \left[m\left({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c\right)+n\left({\mathsf{\omega }}_{0}t+{\mathsf{\theta }}_0\right)\right]\\ +B_{mn}\sin \left[m\left({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c\right)+n\left({\mathsf{\omega }}_{0}t+{\mathsf{\theta }}_0\right)\right]\end{array}\right\}}}\hfill \end{array}$$

(21)

where A₀₀ is the DC offset; A_0n and B_0n are the fundamental component and base-band harmonics; A_m0 and B_m0 are the carrier harmonics; A_mn and B_mn are side-band harmonics.

Based on the double Fourier integral analysis, the fundamental component and harmonics of the inverter leg output can be calculated as

$$A_{mn}+j{B}_{mn}=\frac{1}{2{\mathsf{\pi }}^2}{\displaystyle {\int }_{-\mathsf{\pi }}^{\mathsf{\pi }}{\displaystyle {\int }_{-\frac{\mathsf{\pi }}{2}(1+M\cos y)}^{\frac{\mathsf{\pi }}{2}(1+M\cos y)}2U_{dc}{e}^{j(mx+ny)}dxdy}}$$

(22)

where M is the modulation ratio of PWM.

This paper applies the double Fourier integral analysis to calculate the harmonic voltage of the three-phase inverter in SPWM or SVPWM, by which the harmonic iron loss is estimated accurately.

3.1. Harmonic Components of SPWM

The typical working principle of SPWM is shown in Figure 7. The three-phase sinusoidal references displaced in time by 120°, viz:

$$\{\begin{array}{c}{U}_{az}^{*}=U_0\cos {\mathsf{\omega }}_{0}t=M{U}_{dc}\cos {\mathsf{\omega }}_{0}t\\ U_{bz}^{*}=U_0\cos \left({\mathsf{\omega }}_{0}t-\frac{2}{3}\mathsf{\pi }\right)=M{U}_{dc}\cos \left({\mathsf{\omega }}_{0}t-\frac{2}{3}\mathsf{\pi }\right)\\ U_{cz}^{*}=U_0\cos \left({\mathsf{\omega }}_{0}t+\frac{2}{3}\mathsf{\pi }\right)=M{U}_{dc}\cos \left({\mathsf{\omega }}_{0}t+\frac{2}{3}\mathsf{\pi }\right)\end{array}$$

(23)

where U₀ is the output voltage peak magnitude, M is the modulation ratio, and the reference waveforms are defined with respect to the DC bus center point z.

$$M=\frac{U_0}{U_{dc}}=\frac{\sqrt{u_d^2+u_q^2}}{U_{dc}}=f(i_d,T_e,{\mathsf{\omega }}_r)$$

(24)

The sinusoidal references of SPWM are the fundamental angular in the double Fourier integral analysis, and the harmonic components of the phase output voltage are obtained from Equation (18) as

$$\{\begin{array}{c}\begin{array}{ll}{u}_{az}(t)& =U_{dc}+U_{dc}M\cos {\mathsf{\omega }}_{0}t+\frac{4U_{dc}}{\mathsf{\pi }}{\displaystyle \sum _{m=1}^{\infty }\frac{1}{m}{J}_0(m\frac{\mathsf{\pi }}{2}M)\sin (m\frac{\mathsf{\pi }}{2})}\cos [m({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c)]\\ & +\frac{4U_{dc}}{\mathsf{\pi }}{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{\begin{array}{l}n=-\infty \\ n\ne 0\end{array}}^{n=\infty }\left\{\frac{1}{m}{J}_n(m\frac{\mathsf{\pi }}{2}M)\sin [(m+n)\frac{\mathsf{\pi }}{2}]\cdot \cos [m({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c)+n{\mathsf{\omega }}_{0}t]\right\}}}\end{array}\\ \begin{array}{ll}{u}_{bz}(t)& =U_{dc}+U_{dc}M\cos ({\mathsf{\omega }}_{0}t-\frac{2}{3}\mathsf{\pi })+\frac{4U_{dc}}{\mathsf{\pi }}{\displaystyle \sum _{m=1}^{\infty }\frac{1}{m}{J}_0(m\frac{\mathsf{\pi }}{2}M)\sin (m\frac{\mathsf{\pi }}{2})}\cos [m({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c)]\\ & +\frac{4U_{dc}}{\mathsf{\pi }}{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{\begin{array}{l}n=-\infty \\ n\ne 0\end{array}}^{n=\infty }\left\{\frac{1}{m}{J}_n(m\frac{\mathsf{\pi }}{2}M)\sin [(m+n)\frac{\mathsf{\pi }}{2}]\cdot \cos [m({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c)+n({\mathsf{\omega }}_{0}t-\frac{2}{3}\mathsf{\pi })]\right\}}}\end{array}\\ \begin{array}{ll}{u}_{cz}(t)& =U_{dc}+U_{dc}M\cos ({\mathsf{\omega }}_{0}t+\frac{2}{3}\mathsf{\pi })+\frac{4U_{dc}}{\mathsf{\pi }}{\displaystyle \sum _{m=1}^{\infty }\frac{1}{m}{J}_0(m\frac{\mathsf{\pi }}{2}M)\sin (m\frac{\mathsf{\pi }}{2})}\cos [m({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c)]\\ & +\frac{4U_{dc}}{\mathsf{\pi }}{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{\begin{array}{l}n=-\infty \\ n\ne 0\end{array}}^{n=\infty }\left\{\frac{1}{m}{J}_n(m\frac{\mathsf{\pi }}{2}M)\sin [(m+n)\frac{\mathsf{\pi }}{2}]\cdot \cos [m({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c)+n({\mathsf{\omega }}_{0}t+\frac{2}{3}\mathsf{\pi })]\right\}}}\end{array}\end{array}$$

(25)

where the constant term U_dc is caused by the output voltage definition with respect to the negative DC bus. J_n(ξ) is the Bessel function of the nth order.

From these phase output voltage components, the line-line output voltage components can be presented as

$$\{\begin{array}{c}\begin{array}{ll}{u}_{ab}(t)& =u_{az}(t)-u_{bz}(t)=\sqrt{3}{U}_{dc}M\cos ({\mathsf{\omega }}_{0}t+\frac{\mathsf{\pi }}{6})\\ & +\frac{8U_{dc}}{\mathsf{\pi }}{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=-\infty }^{n=\infty }\frac{1}{m}{J}_n(m\frac{\mathsf{\pi }}{2}M})\sin [(m+n)\frac{\mathsf{\pi }}{2}]}\sin (n\frac{\mathsf{\pi }}{3})\cos [m{\mathsf{\omega }}_{c}t+n({\mathsf{\omega }}_{0}t-\frac{\mathsf{\pi }}{3})+\frac{\mathsf{\pi }}{2}]\end{array}\\ \begin{array}{ll}{u}_{bc}(t)=& u_{bz}(t)-u_{cz}(t)=\sqrt{3}{U}_{dc}M\cos ({\mathsf{\omega }}_{0}t-\frac{\mathsf{\pi }}{2})\\ & +\frac{8U_{dc}}{\mathsf{\pi }}{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=-\infty }^{n=\infty }\frac{1}{m}{J}_n(m\frac{\mathsf{\pi }}{2}M})\sin [(m+n)\frac{\mathsf{\pi }}{2}]}\sin (n\frac{\mathsf{\pi }}{3})\cos [m{\mathsf{\omega }}_{c}t+n({\mathsf{\omega }}_{0}t-\mathsf{\pi })+\frac{\mathsf{\pi }}{2}]\end{array}\\ \begin{array}{ll}{u}_{ca}(t)& =u_{cz}(t)-u_{az}(t)=\sqrt{3}{U}_{dc}M\cos ({\mathsf{\omega }}_{0}t+\frac{5\mathsf{\pi }}{6})\\ & +\frac{8U_{dc}}{\mathsf{\pi }}{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{n=-\infty }^{n=\infty }\frac{1}{m}{J}_n(m\frac{\mathsf{\pi }}{2}M})\sin [(m+n)\frac{\mathsf{\pi }}{2}]}\sin (n\frac{\mathsf{\pi }}{3})\cos [m{\mathsf{\omega }}_{c}t+n({\mathsf{\omega }}_{0}t+\frac{\mathsf{\pi }}{3})+\frac{\mathsf{\pi }}{2}]\end{array}\end{array}$$

(26)

The harmonic components of the line-line output voltage are significantly different from the phase output voltage, since a lot of harmonic cancelation occurs between the phase legs. The line-line output voltage will not have these harmonic components which appear in the phase output voltage.

• Carrier harmonics, which are the same components for all three-phase output voltages.
• Side-band harmonics with even combinations of m ± n, which are eliminated by the $\sin [(m+n)\frac{\mathsf{\pi }}{2}]$ terms in Equation (24).
• Side-band harmonics where n is a multiple of 3.

3.2. Harmonic Components of SVPWM

There are only eight possible switch combinations for a three-phase inverter, and they are shown in Figure 8.

The state of the phase leg is defined as “1” when the phase leg is open, and the state of the phase leg is defined as “0” when the phase leg is closed. The U₀ (000) state and U₇ (111) state correspond to a short circuit on the output, while the other six states can be considered to form stationary vectors in the d-q complex plane. Each stationary vector corresponds to a particular fundamental angular position. The SVPWM applies these eight stationary vectors from an arbitrary target output vector U₀ at any point in time by the summation of a number of these space vectors within one switching period (T_PWM). The space vectors and active times for a different target output vector are shown in

Table 1. Space vector and active time in the SVPWM.

${\mathsf{\omega }}_0\mathbf{t}={\mathsf{\theta }}_0$	Space Vector	Space Vector Active Time
$0\le {\mathsf{\theta }}_0<\frac{\mathsf{\pi }}{3}$	U1	$T_{U1}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0+\frac{\mathsf{\pi }}{6}\right)T_{PWM}$
	U2	$T_{U2}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0-\frac{\mathsf{\pi }}{2}\right)T_{PWM}$
$\frac{\mathsf{\pi }}{3}\le {\mathsf{\theta }}_0<\frac{2\mathsf{\pi }}{3}$	U2	$T_{U2}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0-\frac{\mathsf{\pi }}{6}\right)T_{PWM}$
	U3	$T_{U3}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0-\frac{5\mathsf{\pi }}{6}\right)T_{PWM}$
$\frac{2\mathsf{\pi }}{3}\le {\mathsf{\theta }}_0<\mathsf{\pi }$	U3	$T_{U3}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0-\frac{\mathsf{\pi }}{2}\right)T_{PWM}$
	U4	$T_{U4}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0-\frac{7\mathsf{\pi }}{6}\right)T_{PWM}$
$\mathsf{\pi }\le {\mathsf{\theta }}_0<\frac{4\mathsf{\pi }}{3}$	U4	$T_{U4}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0-\frac{5\mathsf{\pi }}{6}\right)T_{PWM}$
	U5	$T_{U5}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0-\frac{3\mathsf{\pi }}{2}\right)T_{PWM}$
$\frac{4\mathsf{\pi }}{3}\le {\mathsf{\theta }}_0<\frac{5\mathsf{\pi }}{3}$	U5	$T_{U5}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0-\frac{7\mathsf{\pi }}{6}\right)T_{PWM}$
	U6	$T_{U6}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0-\frac{11\mathsf{\pi }}{6}\right)T_{PWM}$
$\frac{5\mathsf{\pi }}{3}\le {\mathsf{\theta }}_0<2\mathsf{\pi }$	U6	$T_{U6}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0-\frac{3\mathsf{\pi }}{2}\right)T_{PWM}$
	U1	$T_{U1}=\frac{U_0}{U_{dc}}\frac{\sqrt{3}}{2}\cos \left({\mathsf{\theta }}_0-\frac{\mathsf{\pi }}{6}\right)T_{PWM}$

. Where U₁ to U₆ are the six space state vectors, respectively, which are shown in Figure 8. And T_U1 to T_U6 are the active times of six space vectors (U₁ to U₆) in one switching period, respectively.

From Table 1, the phase leg reference voltage for SVPWM can be obtained in

Table 2. Phase reference voltage for SVPWM.

${\mathsf{\omega }}_0\mathbf{t}={\mathsf{\theta }}_0$	A Phase Leg	B Phase Leg	C Phase Leg
$0\le {\mathsf{\theta }}_0<\frac{\mathsf{\pi }}{3}$	$\frac{\sqrt{3}}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0+\frac{1}{6}\mathsf{\pi })$	$\frac{\sqrt{3}}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0-\frac{5}{6}\mathsf{\pi })$	$\frac{3}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0+\frac{2}{3}\mathsf{\pi })$
$\frac{\mathsf{\pi }}{3}\le {\mathsf{\theta }}_0<\frac{2\mathsf{\pi }}{3}$	$\frac{3}{2}M{U}_{dc}\cos {\mathsf{\theta }}_0$	$\frac{\sqrt{3}}{2}M{U}_{dc}\sin {\mathsf{\theta }}_0$	$-\frac{\sqrt{3}}{2}M{U}_{dc}\sin {\mathsf{\theta }}_0$
$\frac{2\mathsf{\pi }}{3}\le {\mathsf{\theta }}_0<\mathsf{\pi }$	$\frac{\sqrt{3}}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0-\frac{1}{6}\mathsf{\pi })$	$\frac{3}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0-\frac{2}{3}\mathsf{\pi })$	$\frac{\sqrt{3}}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0+\frac{5}{6}\mathsf{\pi })$
$\mathsf{\pi }\le {\mathsf{\theta }}_0<\frac{4\mathsf{\pi }}{3}$	$\frac{\sqrt{3}}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0+\frac{1}{6}\mathsf{\pi })$	$\frac{\sqrt{3}}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0-\frac{5}{6}\mathsf{\pi })$	$\frac{3}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0+\frac{2}{3}\mathsf{\pi })$
$\frac{4\mathsf{\pi }}{3}\le {\mathsf{\theta }}_0<\frac{5\mathsf{\pi }}{3}$	$\frac{3}{2}M{U}_{dc}\cos {\mathsf{\theta }}_0$	$\frac{\sqrt{3}}{2}M{U}_{dc}\sin {\mathsf{\theta }}_0$	$-\frac{\sqrt{3}}{2}M{U}_{dc}\sin {\mathsf{\theta }}_0$
$\frac{5\mathsf{\pi }}{3}\le {\mathsf{\theta }}_0<2\mathsf{\pi }$	$\frac{\sqrt{3}}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0-\frac{1}{6}\mathsf{\pi })$	$\frac{3}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0-\frac{2}{3}\mathsf{\pi })$	$\frac{\sqrt{3}}{2}M{U}_{dc}\cos ({\mathsf{\theta }}_0+\frac{5}{6}\mathsf{\pi })$

.

Table 2 shows that the phase reference signal for SVPWM is not a continuous function, but is now made up of six segments across a complete fundamental cycle. Therefore, the harmonic calculation for SVPWM will have to become a summation of six integral terms, each spanning 60° of the fundamental signal in the double Fourier integral analysis.

$$A_{mn}+j{B}_{mn}=\frac{1}{2{\mathsf{\pi }}^2}{\displaystyle \sum _{i=1}^6{\displaystyle {\int }_{y_1(i)}^{y_2(i)}{\displaystyle {\int }_{x_1(i)}^{x_2(i)}2V_{dc}{e}^{j(mx+ny)}dxdy}}}$$

(27)

From Equation (22), the harmonic components of the phase output voltage can be obtained as

$$\begin{array}{cc}{u}_{az}(t)& =\frac{A_{00}}{2}+{\displaystyle \sum _{n=1}^{\infty }\left[A_{0n}\cos \left(n{\mathsf{\omega }}_{0}t\right)+B_{0n}\sin \left(n{\mathsf{\omega }}_{0}t\right)\right]}\hfill \\ & +{\displaystyle \sum _{m=1}^{\infty }\left\{A_{m0}\cos \left[m\left({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c\right)\right]+B_{m0}\sin \left[m\left({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c\right)\right]\right\}}\hfill \\ & +{\displaystyle \sum _{m=1}^{\infty }{\displaystyle \sum _{\begin{array}{c}n=-\infty \\ (n\ne 0)\end{array}}^{\infty }\left\{A_{mn}\cos \left[m\left({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c\right)+n{\mathsf{\omega }}_{0}t\right]+B_{mn}\sin \left[m\left({\mathsf{\omega }}_{c}t+{\mathsf{\theta }}_c\right)+n{\mathsf{\omega }}_{0}t\right]\right\}}}\hfill \end{array}$$

(28)

The outer and inner integral limits of Equation (27) are defined in

Table 3. Outer and inner integral limits for SVPWM.

i	y1(i)	y2(i)	x1(i)	x2(i)
1	$\frac{2}{3}\mathsf{\pi }$	$\mathsf{\pi }$	$-\frac{\mathsf{\pi }}{2}[1+\frac{\sqrt{3}}{2}M\cos (y+\frac{\mathsf{\pi }}{6})]$	$\frac{\mathsf{\pi }}{2}[1+\frac{\sqrt{3}}{2}M\cos (y+\frac{\mathsf{\pi }}{6})]$
2	$\frac{1}{3}\mathsf{\pi }$	$\frac{2}{3}\mathsf{\pi }$	$-\frac{\mathsf{\pi }}{2}(1+\frac{3}{2}M\cos y)$	$\frac{\mathsf{\pi }}{2}(1+\frac{3}{2}M\cos y)$
3	0	$\frac{1}{3}\mathsf{\pi }$	$-\frac{\mathsf{\pi }}{2}[1+\frac{\sqrt{3}}{2}M\cos (y-\frac{\mathsf{\pi }}{6})]$	$\frac{\mathsf{\pi }}{2}[1+\frac{\sqrt{3}}{2}M\cos (y-\frac{\mathsf{\pi }}{6})]$
4	$-\frac{1}{3}\mathsf{\pi }$	0	$-\frac{\mathsf{\pi }}{2}[1+\frac{\sqrt{3}}{2}M\cos (y+\frac{\mathsf{\pi }}{6})]$	$\frac{\mathsf{\pi }}{2}[1+\frac{\sqrt{3}}{2}M\cos (y+\frac{\mathsf{\pi }}{6})]$
5	$-\frac{2}{3}\mathsf{\pi }$	$-\frac{1}{3}\mathsf{\pi }$	$-\frac{\mathsf{\pi }}{2}(1+\frac{3}{2}M\cos y)$	$\frac{\mathsf{\pi }}{2}(1+\frac{3}{2}M\cos y)$
6	$-\mathsf{\pi }$	$-\frac{2}{3}\mathsf{\pi }$	$-\frac{\mathsf{\pi }}{2}[1+\frac{\sqrt{3}}{2}M\cos (y-\frac{\mathsf{\pi }}{6})]$	$\frac{\mathsf{\pi }}{2}[1+\frac{\sqrt{3}}{2}M\cos (y-\frac{\mathsf{\pi }}{6})]$

.

The harmonic coefficient can be shown as:

$$\{\begin{array}{c}{A}_{00}=2U_{dc}\\ {A_{0n}+j{B}_{0n}|}_{n>1}=\frac{\sqrt{3}M{U}_{dc}}{\mathsf{\pi }(1-n^2)}[\sin {(\frac{\mathsf{\pi }}{6}n)}^2][2\cos (\frac{2\mathsf{\pi }}{3}n)+1]\\ A_{m0}+j{B}_{m0}=\frac{8U_{dc}}{m{\mathsf{\pi }}^2}\left\{\begin{array}{l}\frac{\mathsf{\pi }}{6}\sin (m\frac{\mathsf{\pi }}{2})[J_0(m\frac{3}{4}\mathsf{\pi }M)+2J_0(m\frac{\sqrt{3}}{4}\mathsf{\pi }M)]\\ +{\displaystyle \sum _{k=1}^{\infty }\frac{2}{k}\sin [(m+k)\frac{\mathsf{\pi }}{2}]\cos (k\frac{\mathsf{\pi }}{2})}\sin (k\frac{\mathsf{\pi }}{6})[J_k(m\frac{3}{4}\mathsf{\pi }M)+2\cos (k\frac{\mathsf{\pi }}{2})J_k(m\frac{\sqrt{3}}{4}\mathsf{\pi }M)]\end{array}\right\}\\ A_{mn}+j{B}_{mn}=\frac{8U_{dc}}{m{\mathsf{\pi }}^2}\left\{\begin{array}{l}\frac{\mathsf{\pi }}{6}\sin [(m+n)\frac{\mathsf{\pi }}{2}][J_n(m\frac{3}{4}\mathsf{\pi }M)+2\cos (n\frac{\mathsf{\pi }}{6})J_n(m\frac{\sqrt{3}}{4}\mathsf{\pi }M)]\\ +{\frac{1}{n}\sin (m\frac{\mathsf{\pi }}{2})\cos (n\frac{\mathsf{\pi }}{2})\sin (n\frac{\mathsf{\pi }}{6})[J_0(m\frac{3}{4}\mathsf{\pi }M)-J_0(m\frac{\sqrt{3}}{4}\mathsf{\pi }M)]|}_{n\ne 0}\\ +{\displaystyle \sum _{\begin{array}{l}k=1\\ k\ne -n\end{array}}^{\infty }\frac{1}{n+k}\sin [(m+k)\frac{\mathsf{\pi }}{2}]\cos [(n+k)\frac{\mathsf{\pi }}{2}]}\sin [(n+k)\frac{\mathsf{\pi }}{6}][J_k(m\frac{3}{4}\mathsf{\pi }M)+2\cos [(2n+3k)\frac{\mathsf{\pi }}{6}]J_k(m\frac{\sqrt{3}}{4}\mathsf{\pi }M)]\\ +{\displaystyle \sum _{\begin{array}{l}k=1\\ k\ne n\end{array}}^{\infty }\frac{1}{n-k}\sin [(m+k)\frac{\mathsf{\pi }}{2}]\cos [(n-k)\frac{\mathsf{\pi }}{2}]}\sin [(n-k)\frac{\mathsf{\pi }}{6}][J_k(m\frac{3}{4}\mathsf{\pi }M)+2\cos [(2n-3k)\frac{\mathsf{\pi }}{6}]J_k(m\frac{\sqrt{3}}{4}\mathsf{\pi }M)]\end{array}\right\}\end{array}$$

(29)

where the constant term A₀₀ is caused by the output voltage definition with respect to the negative DC bus.

3.3. Harmonic Iron Loss of PMSM

As the PMSM is droved by the three-phase PWM inverter, the PWM output voltage of the phase leg in the three-phase inverter will generate the harmonic current in the stator windings of the PMSM, which will cause the harmonic iron loss. The harmonic voltage is calculated with respect to the negative DC bus; hence, the harmonic voltage with respect to the load neutral point can be obtained as

$${\dot{u}}_{a{n}_{nm}}={\dot{u}}_{a{z}_{nm}}-\frac{\left({\dot{u}}_{a{z}_{nm}}+{\dot{u}}_{b{z}_{nm}}+{\dot{u}}_{c{z}_{nm}}\right)}{3}$$

(30)

where ${\dot{u}}_{a{z}_{nm}}$, ${\dot{u}}_{b{z}_{nm}}$ and ${\dot{u}}_{b{z}_{nm}}$ are the harmonic voltages with respect to the negative DC bus in the nth fundamental signal and the mth carrier signal. In addition, ${\dot{u}}_{a{n}_{nm}}$ is the harmonic voltage with respect to the load neutral point in the nth fundamental signal and the mth carrier signal.

Based on the voltage equation of the PMSM, the stator harmonic current can be obtained as

$$I_{s_{nm}}=\left|\frac{{\dot{u}}_{a{n}_{nm}}}{R_s+j{\mathsf{\omega }}_{mn}{L}_s}\right|$$

(31)

where $I_{s_{nm}}$ is the amplitude of the harmonic current in the nth fundamental signal and mth carrier signal.

Similar to the calculation of the fundamental iron loss, the harmonic iron loss can be derived from the Bertotti iron loss formula as

$$P_{Fe\_h}=3\left({\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{\begin{array}{l}n=-\infty \\ n\ne 0\end{array}}^{\infty }{k}_{hd\_mn}{\left(L_s{I}_{S_{mn}}\right)}^2+k_{ep\_mn}{\left(L_s{I}_{S_{mn}}\right)}^{1.5}}}\right)$$

(32)

where L_s is the phase self-inductance of the PMSM; k_{hd_mn} is the coefficient of the equivalent iron hysteresis and eddy losses in the nth fundamental signal and mth carrier signal; and k_{ep_mn} is the coefficient of equivalent iron excess loss in the nth fundamental signal and mth carrier signal, which are shown as

$$\{\begin{array}{c}{k}_{hd\_mn}=\left(k_h{f}_{mn}+\frac{{\mathsf{\pi }}^2\mathsf{\sigma }{k}_d^2}{6}{f}_{mn}^2\right)\left[\frac{{\left(2n_p\right)}^2{V}_t}{{\left({\mathsf{\alpha }}_i{S}_{t}Q\right)}^2}+\frac{V_y}{{\left(2S_y\right)}^2}\right]\\ k_{ep\_mn}=k_e{B}_m^{1.5}{f}_{mn}^{1.5}\left[\frac{{\left(2n_p\right)}^{1.5}{V}_t}{{\left({\mathsf{\alpha }}_i{S}_{t}Q\right)}^{1.5}}+\frac{V_y}{{\left(2S_y\right)}^{1.5}}\right]\end{array}$$

(33)

where f_mn is the frequency in the nth fundamental signal and mth carrier signal.

As the modulation mode affects the harmonic components of the output voltage in the three-phase inverter, the harmonic components of the stator current will be different between SPWM and SVPWM. Hence, the harmonic iron loss will also remain somewhat different between SPWM and SVPWM, and the difference will be greater when either the PWM frequency or modulation ratio M is lower.

4. Maximum Efficiency per Torque Control of PMSM

From Equation (17) and Equation (32), the loss of the PMSM can be obtained as

$$P_{loss}=P_{loss\_f}+P_{Fe\_h}=f({\mathsf{\omega }}_r,i_d,i_q)+f(M)$$

(34)

Additionally, substituting Equation (6) and Equation (24) with Equation (34), the loss of the PMSM can be derived as

$$\begin{array}{cc}{P}_{loss\_PMSM}& =P_{loss\_f}+P_{Fe\_h}\hfill \\ & =f({\mathsf{\omega }}_r,i_d,i_q)+f(M)\hfill \\ & =f(i_d,{\mathsf{\omega }}_r,T_e)\hfill \end{array}$$

(35)

From Equation (35), it can be seen that the loss of the PMSM is a function of the d-axis current i_d, the angular speed ω_r and the electromagnetic torque T_e. Therefore, there must be an optimal flux-weakening d-axis current where the loss of the PMSM can achieve the minimum value in each const operation point (ω_r and T_e is const). The optimal d-axis current i_d^* can be obtained from Equation (36) as

$${\frac{\partial P_{loss\_PMSM}}{\partial i_d}|}_{i_d=i_d^{*}}^{{\mathsf{\omega }}_r=const,T_e=const}=0$$

(36)

The MEPT control can make the d-axis flux-weakening current remain the optimal value i_d^* and achieve the maximum efficiency of the PMSM in the whole operation range. As Equation (36) makes it too difficult to acquire the analytical solution of the optimal current, this paper applied the golden section method to obtain the numerical solution of the optimal current. The golden section is a technique for finding the minimum value of a unimodal function by successively narrowing the range of values inside which the minimum is known to exist. The flowchart of the golden section procedure is shown in Figure 9, where $\mathsf{\phi }$ is the golden ratio: $\mathsf{\phi }=\frac{1+\sqrt{5}}{2}=1.618$.

5. Experimental Results and Discussion

The model parameters of the SPMSM are listed in

Table 4. Model parameters of SPMSM.

Parameter	Value
rated power	4 kW
rated speed	2000 rpm
max power	5 kW
poles	10
phase resistance	0.12 Ω
phase inductance	1.67 mH
DC bus voltage	270 V
stator outer diameter	150 mm
Stator inner diameter	100 mm
axial length	68 mm
PWM frequency	5 kHz

.

To verify the proposed control strategy, the experiment is implemented by a PMSM test platform, which is shown in Figure 10.

The efficiency of the PMSM in SPWM is shown in Figure 11.

Figure 11a,b show the efficiency of the PMSM using the traditional i_d = 0 control and proposed MEPT control, respectively, where the maximum efficiency of the PMSM using i_d = 0 control is 94%. It can be seen that the MEPT control can broaden the high-efficiency field of the PMSM and obtain a higher efficiency in each operation condition of the PMSM. It is shown in Figure 11c that the efficiency can be increased in the whole operation range of the PMSM and the maximum efficiency enhancement is 0.36%.

The efficiency of the PMSM in SVPWM is shown in Figure 12.

The efficiency of the PMSM using the traditional i_d = 0 control and proposed MEPT control is shown in Figure 12. From Figure 12a,b, the MEPT control can also enhance the high-efficiency field of the PMSM. Compared with the efficiency of the PMSM using the i_d = 0 control, Figure 12c shows that the efficiency of the PMSM is increased by the MEPT control in the whole operation range, and the maximum efficiency enhancement is 0.51%.

From Figure 11 and Figure 12, it can be seen that the operation speed range is different between SPWM and SVPWM, because the DC bus voltage utilization of SVPWM is higher than SPWM. It can be also seen that the efficiency optimization performance of MEPT control in SVPWM is greater than the performance in SPWM.

It is generally observed that the MEPT control strategy can increase the efficiency performance of the PMSM in the whole operation range in both SPWM and SVPWM. For the experimental 5 kW high-efficiency PMSM, although the motor efficiency has achieved as great as 94% efficiency using the traditional i_d = 0 control, the proposed MEPT control can also enhance the motor efficiency by 0.51%. The MEPT control strategy is a fast and efficient way to increase the efficiency of the PMSM and decrease the loss of the motor system without damage to the dynamic performance in the aviation and aerospace field.

6. Conclusions

This paper has proposed a novel analytical loss model of the PMSM for loss estimation. The analytical loss model can take into account both fundamental loss and harmonic loss. The fundamental copper loss and fundamental iron loss are presented in the fundamental loss model. As the PMSM is fed by a three-phase inverter, this paper applies double Fourier integral analysis to calculate the harmonic components of the phase output voltage in either SPWM or SPVWM accurately. From the Bertotti iron loss formula, this paper creates the harmonic iron loss model of the PMSM in a fast and simple way.

Based on the analytical loss model, an efficiency optimization control strategy named MEPT is proposed in this paper, and it can optimize the fundamental loss and harmonic loss together using the optimal flux-weakening d-axis current. The analytical solution is so difficult that a golden section method is applied to obtain the optimal current in each operation condition. Experimental results are implemented to demonstrate how, in comparison to a more traditional i_d = 0 control, the MEPT control can increase the efficiency of the PMSM without any reduction of the dynamic performance in both SPWM and SVPWM. Additionally, the results also show that the MEPT control in SVPWM leads to a greater efficiency enhancement than SPWM.