Research on a Composite Power-Superimposed Ultrasonic Vibrator for Wire Drawing
Abstract
:1. Introduction
2. Structure and Mathematical Model
2.1. Structure and Working Principle
| Dimension Parameters (mm) | Material Parameters (7A04) | |||||||
|---|---|---|---|---|---|---|---|---|
| L0 | L | L1 | R0 | R | E (N/mm2) | C (mm/s) | P (g/mm3) | v |
| 20 | 40 | 20 | 10 | 20 | 6.85 × 10−4 | 5.1 × 106 | 2700 | 0.34 |


2.2. Vibration Equations

2.3. Amplification Ratio


3. Regulation Analysis of the Power-Superimposed Vibrator
3.1. Modal Analysis and Harmonic Analysis
| Order | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Frequency/Hz | 20,096 | 21,912 | 22,855 | 22,859 | 23,474 | 23,476 |



3.2. Transient Analysis and Driving Methods




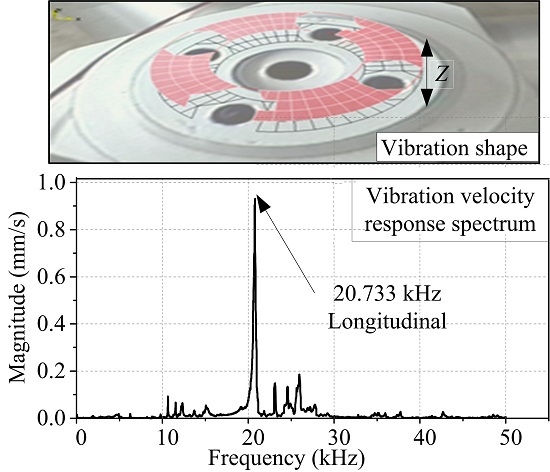
4. Fabrication and Measurement



5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Parris, W.; Rosenberg, H.W. High Strength Titanium Alloys. U.S. Patent 3,802,877, 1974. [Google Scholar]
- Lide, D.R. Handbook of chemistry and physics, 83rd ed.; CRC Press: Boca Raton, FL, USA, 2002; p. 504. [Google Scholar]
- Moiseyev, V.N. Titanium Alloys: Russian Aircraft and Aerospace Applications; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Tang, L.; Du, Y. Experimental study on green electrical discharge machining in tap water of Ti-6Al-4V and parameters optimization. Int. J. Adv. Manuf. Technol. 2014, 70, 469–475. [Google Scholar] [CrossRef]
- Ma, J.; Andrus, P.; Condoor, S.; Lei, S. Numerical investigation of effects of cutting conditions and cooling schemes on tool performance in up milling of Ti-6Al-4V alloy. Int. J. Adv. Manuf. Technol. 2015, 78, 361–383. [Google Scholar] [CrossRef]
- Kumar, J.; Khamba, J. Modeling the material removal rate in ultrasonic machining of titanium using dimensional analysis. Int. J. Adv. Manuf. Technol. 2010, 48, 103–119. [Google Scholar] [CrossRef]
- Siegert, K.; Möck, A. Wire drawing with ultrasonically oscillating dies. J. Mater. Process. Technol. 1996, 60, 657–660. [Google Scholar] [CrossRef]
- Yao, Z.; Kim, G.Y.; Faidley, L.; Zou, Q.; Mei, D.; Chen, Z. Effects of superimposed high-frequency vibration on deformation of aluminum in micro/meso-scale upsetting. J. Mater. Process. Technol. 2012, 212, 640–646. [Google Scholar] [CrossRef]
- Siddiq, A.; El Sayed, T. Ultrasonic-assisted manufacturing processes: Variational model and numerical simulations. Ultrasonics 2012, 52, 521–529. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.W.; Baek, D.K.; Ko, T.J. Chipping minimization in drilling ceramic materials with rotary ultrasonic machining. Int. J. Adv. Manuf. Technol. 2014, 72, 1527–1535. [Google Scholar] [CrossRef]
- Blaha, F.; Langenecker, B. Tensile deformation of zinc crystal under ultrasonic vibration. Naturwissenschaften 1955, 42, 556. [Google Scholar] [CrossRef]
- Siddiq, A.; El Sayed, T. Acoustic softening in metals during ultrasonic assisted deformation via cp-fem. Mater. Lett. 2011, 65, 356–359. [Google Scholar] [CrossRef]
- Mori, E.; Inoue, M. Effects of drawing speed and backward tension application of ultrasonic vibration to metal wire drawing (2nd report). J. JSTP 1970, 11, 144. [Google Scholar]
- Murakawa, M.; Kaewtatip, P.; Jin, M. Skin pass wire drawing of stainless steel with chlorine-free lubricant with the aid of ultrasonic vibration. Trans. N. Am. Manuf. Res. Inst. SME 2000, 28, 75–80. [Google Scholar]
- Qi, H.; Shan, X.; Xie, T. Design and experiment of the high speed wire drawing with ultrasound. Chin. J. Mech. Eng. 2009, 4, 580–586. [Google Scholar] [CrossRef]
- Haiqun, Q.I.; Zhang, H.; Song, X.; Wang, L.; Yin, Z.; Shan, X. Experimental research of the wire drawing with composite ultrasonic vibration imposed by anti-pull. J. Harbin Eng. Univ. 2013, 34, 402–408. [Google Scholar]
- Yang, C.; Shan, X.; Xie, T. A new piezoelectric ceramic longitudinal-torsional composite ultrasonic vibrator for wire drawing. Ceram. Int. 2015, 41, S625–S630. [Google Scholar] [CrossRef]
- Huang, D. Design of vibration system for ultrasonic wave vibrator. J. Vib. Shock 2005, 24, 107–108. [Google Scholar]
- Yang, C.; Shan, X.; Xie, T. Titanium wire drawing with longitudinal-torsional composite ultrasonic vibration. Int. J. Adv. Manuf. Technol. 2015. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Shan, X.; Guo, K.; Xie, T. Research on a Composite Power-Superimposed Ultrasonic Vibrator for Wire Drawing. Appl. Sci. 2016, 6, 32. https://doi.org/10.3390/app6020032
Liu S, Shan X, Guo K, Xie T. Research on a Composite Power-Superimposed Ultrasonic Vibrator for Wire Drawing. Applied Sciences. 2016; 6(2):32. https://doi.org/10.3390/app6020032
Chicago/Turabian StyleLiu, Shen, Xiaobiao Shan, Kai Guo, and Tao Xie. 2016. "Research on a Composite Power-Superimposed Ultrasonic Vibrator for Wire Drawing" Applied Sciences 6, no. 2: 32. https://doi.org/10.3390/app6020032
APA StyleLiu, S., Shan, X., Guo, K., & Xie, T. (2016). Research on a Composite Power-Superimposed Ultrasonic Vibrator for Wire Drawing. Applied Sciences, 6(2), 32. https://doi.org/10.3390/app6020032