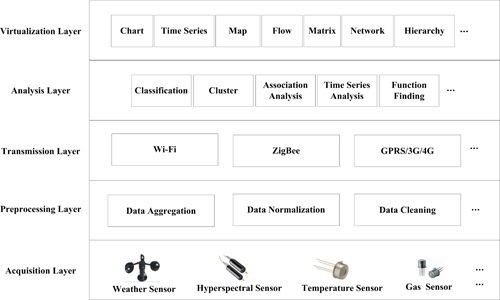
1. Introduction
Progress in wireless communication and microelectronic devices has led to the development of low-power sensors and the deployment of large-scale sensor networks [
1]. Wireless sensor networks (WSNs) have been developed and applied to many fields, such as smart grid [
2], agriculture [
3,
4], environment monitoring [
5,
6], and the military [
7]. In these applications, because of the large number and wide distribution of sensors, the data from sensors is characterized by high dimension, large amount, and wide distribution [
8,
9]. How to find useful knowledge from high dimensional, massive and distributed data has become a key issue of data mining in wireless sensor networks [
8,
9].
Recently, all kinds of approaches, including clustering [
10,
11], association rules [
12] and classification [
13,
14], have been successfully applied in wireless sensor networks. Function model finding is also an important branch of data mining. The function finding technique for all kinds of application data from WSNs can reveal the essence and phenomenon in the application. However, in the existing references, function finding is rarely mentioned in WSNs.
The existing function model discovery algorithms mainly include the regression, the evolution algorithms, and so on. Generally, traditional regression methods assumed that the function type was known, and then the least squares method or its improved methods for parameter estimation were used to determine the functional model [
15]. These traditional regression methods needed to depend on
a priori knowledge and a lot of subjective factors. Moreover, these methods have high time complexity and low computation efficiency for complex and high-dimensional datasets from WSNs. To solve these problems, Li
et al. and Koza
et al. used genetic programming (GP) for mathematical modeling and obtained good experimental results [
16,
17]. Yeun
et al. proposed a method which dealt with smooth fitting problem by GP [
18]. In order to fit data points to curves in CAD (Computer Aided Design)/CAM (Computer Aided Manufacturing), Gálvez
et al. present a new hybrid evolutionary approach (GA-PSO) for B-spline curve reconstruction [
19]. Meanwhile, GP, genetic algorithm (GA) or hybrid evolutionary algorithms also avoid the defect of traditional statistical methods’ selected function models in advance. However, the efficiency of function model mined by GP, GA or hybrid evolutionary algorithms was low. Thus, a new algorithm called gene expression programming (GEP) was proposed [
20]. Compared with GP, the efficiency of complex functions mined based on GEP was improved 4–6 times.
Therefore, in order to reveal the inherent nature of the sensor data, this paper proposes a function finding algorithm using gene expression programming (FF-GEP). In FF-GEP, an adaptive population generation strategy is put forward. The strategy avoids the local optimum of GEP population. However, thousands of distributed sensor nodes, and the unstable wireless communication environment make traditional centralized function mining algorithms difficult to meet the needs of function mining in wireless sensor networks. Traditional centralized FF-GEP is unable to meet the requirement of function finding in wireless sensor networks. In order to better find functions for complex, massive and high-dimensional sensor data, on the basis of FF-GEP, this paper presents distributed global function model finding for wireless sensor networks data (DGFMF-WSND).
The main contributions of this paper are summarized as follows: (1) we present the function finding algorithm using gene expression programming for wireless sensor networks data (FF-GEP) in order to prevent GEP from the local optimum; (2) we solve the generation of the global function model in distributed function finding and provide a global model generation algorithm based on unconstrained and nonlinear least squares (GMG-UNLS); (3) on the basis of FF-GEP and GMG-UNLS, we put forward distributed global function model finding for wireless sensor networks data (DGFMF-WSND); and (4) we describe simulated experiments that have been done and provides performance analysis results.
The content of the paper is organized as follows.
Section 2 discusses prior work related to data mining in WSNs and function mining.
Section 3 introduces the function finding algorithm using gene expression programming for wireless sensor networks data.
Section 4 emphasizes the distributed global function model finding for wireless sensor networks data.
Section 5 represents experiments and performance analysis. Finally, conclusions are given in
Section 6.
4. Distributed Global Function Model Finding for Wireless Sensor Networks Data
4.1. Algorithm Idea
In WSNs, because the number of sensors is very large and sensors are physically deployed in a very distributed fashion, traditional centralized function model finding algorithms will undoubtedly increase transmission bandwidth, network delay and probability of data packet loss, and also reduce the efficiency of function model finding. Meanwhile, centralized analysis for massive data in WSNs will also add pressure to the data storage so that traditional centralized function model finding algorithms are difficult to apply in wireless sensors networks.
Grid is a high performance and distributed computing platform with good self-adaptability and scalability, and provides favorable computing and analysis capability for massive or distributed data sets. Grid could provide strong analysis and computing power with distributed data mining and knowledge discovery. In view of advantages of grid computing, on the basis of FF-GEP, this paper presents distributed global function model finding for wireless sensor networks data (DGFMF-WSND) which combines with global model generation and grid services.
Suppose that data on each grid node are homogeneous and the attributes that are contained in each of datasets on the computing nodes are same in this paper. The algorithm idea is divided into some sub-processes. Firstly, algorithms proposed in this paper are wrapped as grid services and deployed on each grid node. Meanwhile, a local function model is obtained by performing FF-GEP algorithm service on each grid node in parallel. Lastly, the local function model of each node is transmitted to the specified node to generate a global model and returned to the user.
4.2. Global Model Generation Algorithm Based on Unconstrained Nonlinear Least Squares
The traditional distributed data mining algorithm mainly includes two steps: (1) analyzing local data and generating a local function model; (2) global function model is obtained by integrating different local function models. How to get the global function model from the local function model has not been investigated in earlier work. This paper presents a global model generation algorithm based on unconstrained nonlinear least squares (GMG-UNLS).
Definition 3. In WSNs, we propose the number of the sensor node and sink node are k and n, respectively. For each sink node, it contains a sensor data set , where and represents target value for each sensor data set. Then, the set of each sink node can be obtained yielding to GEP by employing the approach of function model mining, such that . Hence, is the local function model with m-dimension of the i-th sink node.
Definition 4. Suppose that there exist n sink nodes and , where . There exists a set of constants such that . Thus, is called global function model.
Lemma 1. Given that there exist n local function model with m-dimension in WSNs, and sample datasets on each sink node. There exists a set of constants such that value of is minimum, where .
Proof: Set
. Then
where
and
are constants. Denote
Substituting Equation (3) into Equation (2), we have that
Because is a two time polynomial of , and composed of basic elementary functions, and differentiable.
Hence, the partial derivative of
with respect to
exists, respectively. The Equations (5)–(7) hold.
Solving
such that value of
is minimum. Set
. Thus, Equation (8) can be obtained.
Denote
Then Equation (8) can be rewritten as
. Because of the randomness of data acquisition and function model finding using GEP in wireless sensor networks, there are no two identical or proportional row vectors in the matrix
B so that the determinant of matrix
B is not equal to 0. According to definition of rank of a matrix, we have that
. Therefore, non homogeneous linear equations
exist unique solution
. According to the theorem and deduction of the corresponding calculation of determinant [
46], we have that
, where
The proof is completed.
Based on Lemma 1, this paper proposes global model generation algorithm based on unconstrained nonlinear least squares (GMG-UNLS). The steps of GMG-UNLS are shown as follows:
| Algorithm 3. GMG-UNLS |
| Input: local Function Model , k sample data; |
| Output: global Function Model ; |
| Begin { |
| 1. double ;//Defining n real variables. |
| 2. Set . //Building global function equation. |
| 3. Set ;//Building function model, where is target value for k sample data. |
| 4. ; // Substituting k sample data into . |
| 5. , ; // is obtained by solving non homogeneous linear equations. |
| 6. return ;}// Substituting into and returning . |
The time-consumption of GMG-UNLS focuses on solution of . The time complexity of GMG-UNLS is .
4.3. Description of DGFMF-WSND
Firstly, local function model is solved by FF-GEP on each grid node. Then, global function model is obtained by GMG-UNLS. In order to achieve DGFMF-WSND, firstly, WSDL document which describes FF-GEP is defined. On this basis, server program of DGFMF-WSND is prepared and various XML documents and properties files of the grid service are released. Finally, Gar package is compiled by ant tool, and the service is deployed in the Tomcat container. The users can access the service by writing the client program.
A whole algorithm based on grid service includes client and server. DGFMF-WSND is described respectively from client and server. The description of whole algorithm is listed as follows.
| Algorithm 4. DGFMF-WSND |
| Input: GEPGSH, popSize; maxGen; maxFitness; , , , ; |
| Output: Global Function; |
| Begin { |
| Server: |
| 1. ReceivePara (T, GEPParas, i, GEPGSH); // Parameters are received from ith client according to GEPGSH. |
| 2. InitPop (Pop S); //Initializing population of FF-GEP. |
| 3. LocalFunction (i) = FF-GEP (popSize; maxGen; maxFitness; , , , ); |
| Client: |
| 4. T = Read (SampleData); |
| 5. int gridcodes = SelectGridCodes (); |
| 6. for (int i = 0; i < gridcodes; i++) { |
| 7. TransPara (T, GEPParas, i, GEPGSH); //Transmitting parameters to server. |
| 8. TransService (LocalFunction [i]);} |
| 9. GlobalFunction = GMG-UNLS (LocalFunction); |
| 10. return Global Function;} |
For the distributed algorithm, time-consumption of the algorithm is an important index which must be considered in the design and implementation. From Algorithm 3, we know that execution time of the DGFMF-WSND algorithm includes time of FF-GEP algorithm on each grid node, time of transmission parameters and GMG-UNLS algorithm. In a LAN environment, the time of transmission parameters can be ignored.
Let total time of the DGFMF-WSND algorithm be
, time of FF-GEP on each grid node be
, time of data transmission be
, time of GMG-UNLS algorithm be
. Then Equation (10) is shown as following:
Time of DGFMF-WSND can be very convenient to take on calculation and evaluation by Equation (10).
6. Comparative Analysis
To better evaluate degree of fitting of the proposed algorithm, the evaluation indexes are shown as follows.
Definition 5. Let , and be predicted value, real value and mean value of the i-th original data, respectively. Let be sum of squares for regression, be sum of squares for total. Then is called coefficient of determination.
Note that the bigger the value of , the better the function model.
Definition 6. Let be real maximum fitness value, be model-based maximum fitness value. If , then the corresponding algorithm is convergent.
Due to , such that . In this paper, set .
Definition 7. Let be time-consumption of DGFMF-WSND in a single machine environment, be time-consumption of DGFMF-WSND in parallel computing environment. Then is called speed-up ratio.
Where is mainly used to measure the performance and effect of DGFMF-WSND.
Definition 8. Let be time-consumption to perform dataset with an increase of m times on a cluster with an increase of m times, be time-consumption of the original dataset. Then is called scale-up ratio.
Definition 9. Suppose that the algorithm runs N times independently, and , where be the i-th model-based maximum fitness value. Then, by Definition 6, it is clear that the i-th run of the algorithm is convergent. Thus, the sum of the number of algorithm convergence is called number of convergence of the algorithm.
Definition 10. Suppose that the algorithm runs N times independently, represents the corresponding number of generation when the algorithm is convergent under the condition of the i-th run. Thus, is called average number of convergence generation.
Note that the smaller number of convergence is, the faster convergence speed is.
Example 1: To compare the performance of ACO (Ant Colony Optimization) [
50], SA (Simulated Annealing) [
51], GP [
16], GA [
17], GEP [
20] and FF-GEP, for four datasets in
Table 1, the four algorithms run 50 times independently, and the maximum number of generation of four algorithms is 5000. By Definition 6,
Figure 5 shows comparison of number of convergence for GP, GA, GEP and FF-GEP. Comparison of average generation of convergence for GP, GA, GEP and FF-GEP are shown in
Figure 6. Meanwhile,
Table 2 shows comparison of value of
for four test datasets in
Table 1 based on the four algorithms. Degree of fitting between model value and real value of four test datasets in
Table 1 based on FF-GEP is shown
Figure 7 without taking into account the time-consumption.
Figure 5.
Comparison of number of convergence for ACO (Ant Colony Optimization), SA(Simulated Annealing), genetic programming (GP), genetic algorithm (GA), gene expression programming (GEP) and function finding algorithm using gene expression programming (FF-GEP).
Figure 5.
Comparison of number of convergence for ACO (Ant Colony Optimization), SA(Simulated Annealing), genetic programming (GP), genetic algorithm (GA), gene expression programming (GEP) and function finding algorithm using gene expression programming (FF-GEP).
Figure 6.
Comparison of average number of convergence generation for ACO (Ant Colony Optimization), SA(Simulated Annealing), genetic programming (GP), genetic algorithm (GA), gene expression programming (GEP) and function finding algorithm using gene expression programming (FF-GEP).
Figure 6.
Comparison of average number of convergence generation for ACO (Ant Colony Optimization), SA(Simulated Annealing), genetic programming (GP), genetic algorithm (GA), gene expression programming (GEP) and function finding algorithm using gene expression programming (FF-GEP).
Table 2.
Comparison of value of for four test datasets based on ACO (Ant Colony Optimization), SA(Simulated Annealing), genetic programming (GP), genetic algorithm (GA), gene expression programming (GEP) and function finding algorithm using gene expression programming (FF-GEP).
Table 2.
Comparison of value of for four test datasets based on ACO (Ant Colony Optimization), SA(Simulated Annealing), genetic programming (GP), genetic algorithm (GA), gene expression programming (GEP) and function finding algorithm using gene expression programming (FF-GEP).
| Datasets | Algorithms |
|---|
| ACO | SA | GP | GA | GEP | FF-GEP |
|---|
| LOPEX93 | 0.8355 | 0.8291 | 0.8700 | 0.8490 | 0.9118 | 0.9381 |
| EUNITE | 0.8914 | 0.8901 | 0.9187 | 0.8926 | 0.9263 | 0.9575 |
| GSADD | 0.7012 | 0.6997 | 0.7393 | 0.7035 | 0.8321 | 0.8686 |
| DLS | 0.7801 | 0.7729 | 0.7903 | 0.7844 | 0.88 | 0.9097 |
From
Figure 5, for
LOPEX93, EUNITE, GSADD and DLS datasets, compared with ACO, SA, GP, GA and GEP, number of convergence for FF-GEP maximally increases by 47.06%, 29.73%, 54.55% and 51.72%. In
Figure 6, it is shown that for
LOPEX93, EUNITE, GSADD and DLS datasets, compared with ACO, SA, GP, GA and GEP, average number of convergence generation for FF-GEP drops by 11.44%, 14.31%, 21.53% and 19.82%. This is mainly because, in FF-GEP, adaptive population generation strategy based on collaborative evolution of sub-population is applied to dynamically increase population size and diversity of individual so as to improve the probability of the global optimal solution and convergence speed.
In
Table 2, it is shown that for
LOPEX93, EUNITE, GSADD and DLS datasets, compared with ACO, SA, GP, GA and GEP, value of
based on FF-GEP increases by 11.62%, 7.04%, 19.45% and 15.04%, respectively; and by Definition 5, value of
based on FF-GEP is 0.9381, 0.9575, 0.8686 and 0.9097, respectively. It means that function model for all test datasets based on FF-GEP is best and can fit sample data well. From
Figure 7, using FF-GEP, we can see that for
LOPEX93, EUNITE, GSADD and DLS dataset, the maximum error between real value and model value is 1.1804, 0.9135, 0.9639 and 0.9515, respectively, and the minimum error is 0.0007, 0.0071, 0.0114 and 0.0251, respectively. It can be seen that the model has high prediction accuracy.
Example 2: In order to better evaluate performance of algorithm, Example 2 focuses on comparison of average time-consumption and fitting degree between real value and model value.
Figure 8 shows average time-consumption of ACO, SA, GP, GA, GEP and FF-GEP. Average time-consumption of DGFMF-WSND with the increase of number of computing nodes is shown in
Figure 9. Comparison of value of
for LOPEX 93, EUNITE, GSADD and DLS datasets with the increase of number of computing nodes is shown in
Figure 10.
Figure 11 shows fitting degree between model value and real value of four test datasets in
Table 1 based on DGFMF-WSND on six computing nodes.
Figure 7.
Comparison between model value and real value of four test datasets in
Table 1 using gene expression programming (GEP) and function finding algorithm using gene expression programming (FF-GEP). (
a) Comparison between model value and real value of LOPEX93 datasets using GEP and FF-GEP; (
b) comparison between model value and real value of EUNITE datasets using GEP and FF-GEP; (
c) comparison between model value and real value of GSADD datasets using GEP and FF-GEP; and (
d) comparison between model value and real value of DLS datasets using GEP and FF-GEP.
Figure 7.
Comparison between model value and real value of four test datasets in
Table 1 using gene expression programming (GEP) and function finding algorithm using gene expression programming (FF-GEP). (
a) Comparison between model value and real value of LOPEX93 datasets using GEP and FF-GEP; (
b) comparison between model value and real value of EUNITE datasets using GEP and FF-GEP; (
c) comparison between model value and real value of GSADD datasets using GEP and FF-GEP; and (
d) comparison between model value and real value of DLS datasets using GEP and FF-GEP.
Figure 8.
Comparison of average time-consumption of ACO (Ant Colony Optimization), SA(Simulated Annealing), genetic programming (GP), genetic algorithm (GA), gene expression programming (GEP) and function finding algorithm using gene expression programming (FF-GEP) for four datasets.
Figure 8.
Comparison of average time-consumption of ACO (Ant Colony Optimization), SA(Simulated Annealing), genetic programming (GP), genetic algorithm (GA), gene expression programming (GEP) and function finding algorithm using gene expression programming (FF-GEP) for four datasets.
Figure 9.
Comparison of average time-consumption of DGFMF-WSND for four datasets with the increase of number of computing nodes.
Figure 9.
Comparison of average time-consumption of DGFMF-WSND for four datasets with the increase of number of computing nodes.
From
Figure 8, we know that for
LOPEX93, EUNITE, GSADD and
DLS datasets, compared with ACO, average time-consumption of FF-GEP drops by 51.57%, 44.3%, 70.05% and 65.03%, respectively, compared with SA, average time-consumption of FF-GEP drops by 51.84%, 44.5%, 70.29% and 63.89%, respectively, and compared with GEP, average time-consumption of FF-GEP drops by 26.01%, 4.34%, 58.03% and 42.7%, respectively, in contrast to GP, decreases by 52.03%, 43.58%, 70.57% and 65.38%, respectively. While for
LOPEX93, EUNITE, GSADD and
DLS, average time-consumption of FF-GEP drops by 50.54%, 37.48%, 66.36% and 63.2% respectively in contrast to GA. This means that for
LOPEX93, EUNITE, GSADD and
DLS, FF-GEP outperforms all other algorithms on average time-consumption, followed by GEP. Especially, for
GSADD dataset, average time-consumption of FF-GEP declines most quickly, and while, for
EUNITE dataset, average time-consumption of FF-GEP declines most slowly. This is mainly because that compared with the other datasets, number of attributes of
GSADD dataset is maximum, and number of attributes and instances of
EUNITE dataset is minimum. Meanwhile, FF-GEP adopts adaptive population generation strategy based on collaborative evolution of sub-population to increase convergence speed.
Figure 9 shows that with the increasing of number of computing nodes, average time-consumption of DGFMF-WSND drops gradually for
LOPEX93, EUNITE, GSADD and
DLS datasets. However, when number of computing nodes is increased from 7 to 10, average time-consumption of DGFMF-WSND will increase for all test datasets. This is mainly because that with the increasing of number of computing nodes, time of data transmission and global function generation will continue to increase so that total time-consumption of DGFMF-WSND will increase according to Equation (10). The decrease of time-consumption and the improvement of prediction accuracy of DGFMF-WSND will be helpful to find domain knowledge from massive and distributed wireless sensor network data.
In
Figure 10, it is shown that with the increasing of number of computing nodes, a value of
for four datasets in
Table 1 based on DGFMF-WSND increases gradually. According to Definition 5, we know that the bigger the value of
, the better the function model. When number of computing nodes is increased from 1 to 10, for
LOPEX93, EUNITE, GSADD and
DLS datasets, maximum value of
is 0.97, 0.9994, 0.9201 and 0.9786, respectively. This means that with the increasing number of computing nodes, a global function model based on DGFMF-WSND can fit sample data well. From
Figure 11, we can see that for
LOPEX93, EUNITE, GSADD and
DLS datasets, the maximum error between real value and model value is 0.7667, 0.6429, 0.915 and 0.7333, respectively, and the minimum error is 0.0359, 0.0106, 0.0107 and 0.0018, respectively. It can be seen that the global function model has high prediction accuracy.
Figure 10.
Comparison of value of
for four test datasets in
Table 1 based on distributed global function model finding for wireless sensor networks data (DGFMF-WSND) with the increase of number of computing nodes.
Figure 10.
Comparison of value of
for four test datasets in
Table 1 based on distributed global function model finding for wireless sensor networks data (DGFMF-WSND) with the increase of number of computing nodes.
Example 3: To reflect the parallel performance of DGFMF-WSND, LOPEX93 and EUNITE datasets in
Table 1 are expanded 1000, 2000, 4000 and 8000 times to respectively form four new datasets. Comparison of speed-up ratio of DGFMF-WSND for the four new datasets with the increase of number of computing nodes is shown in
Figure 12.
Figure 13 shows comparison of scale-up ratio of DGFMF-WSND for LOPEX93 and EUNITE datasets with the increase of number of computing nodes.
From
Figure 12, with the increasing of number of computing nodes, speed-up ratio of DGFMF-WSND is increasing, and when size of the
LOPEX93 and
EUNITE dataset is expanded 8000 times, speed-up ratio of DGFMF-WSND is close to the linear increase. We know that change rate of speed-up ratio of an excellent parallel algorithm is close to 1. However, in concrete application, with the increasing of number of computing nodes, time-consumption of information transmission between node and node also increasing, linear speed-up ratio is very difficult to achieve.
Figure 13 shows that for
LOPEX93 and
EUNITE, maximum scale-up ratio reaches 0.91 and 0.98, respectively; however, with the increasing of the number of computing nodes, scale-up ratio of DGFMF-WSND decreases gradually, while the slope of the decrease gets smaller. This means that the scalability of DGFMF-WSND is better.
Figure 11.
Comparison between model value and real value of four test datasets in
Table 1 based on DGFMF-WSND. (
a) Comparison between model value and real value of LOPEX93 datasets based on DGFMF-WSND; (
b) comparison between model value and real value of EUNITE datasets based on DGFMF-WSND ; (
c) comparison between model value and real value of GSADD datasets based on DGFMF-WSND; and (
d) comparison between model value and real value of DLS datasets based on DGFMF-WSND.
Figure 11.
Comparison between model value and real value of four test datasets in
Table 1 based on DGFMF-WSND. (
a) Comparison between model value and real value of LOPEX93 datasets based on DGFMF-WSND; (
b) comparison between model value and real value of EUNITE datasets based on DGFMF-WSND ; (
c) comparison between model value and real value of GSADD datasets based on DGFMF-WSND; and (
d) comparison between model value and real value of DLS datasets based on DGFMF-WSND.
Figure 12.
Comparison of speed-up ratio of DGFMF-WSND for two datasets with the increase of number of computing nodes. (a) Comparison of speed-up ratio of DGFMF-WSND for LOPEX93 datasets with the increase of number of computing nodes; and (b) comparison of speed-up ratio of DGFMF-WSND for EUNITE datasets with the increase of number of computing nodes.
Figure 12.
Comparison of speed-up ratio of DGFMF-WSND for two datasets with the increase of number of computing nodes. (a) Comparison of speed-up ratio of DGFMF-WSND for LOPEX93 datasets with the increase of number of computing nodes; and (b) comparison of speed-up ratio of DGFMF-WSND for EUNITE datasets with the increase of number of computing nodes.
Figure 13.
Comparison of scale-up ratio of DGFMF-WSND for LOPEX93 and EUNITE datasets with the increase of number of computing nodes.
Figure 13.
Comparison of scale-up ratio of DGFMF-WSND for LOPEX93 and EUNITE datasets with the increase of number of computing nodes.