Next Article in Journal
A Novel Bearing Lubricating Device Based on the Piezoelectric Micro-Jet
Previous Article in Journal
Frequency-Dependent Amplitude Panning for the Stereophonic Image Enhancement of Audio Recorded Using Two Closely Spaced Microphones
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 6
Issue 2
10.3390/app6020040
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Microfluidic Device for Hydrodynamic Trapping and Manipulation Platform of a Single Biological Cell

by
Amelia Ahmad Khalili
1,
Mohd Ridzuan Ahmad
1,*,
Masaru Takeuchi
2,
Masahiro Nakajima
2,
Yasuhisa Hasegawa
2 and
Razauden Mohamed Zulkifli
3
1
Department of Control and Mechatronic Engineering, Faculty of Electrical Engineering, Universiti Teknologi Malaysia, Skudai, Johor 81310, Malaysia
2
Department of Micro-Nano Systems Engineering, Nagoya University, Furo-cho, Chikusa-ku, Nagoya 464-8603, Aichi, Japan
3
Department of Bioscience and Health Sciences, Faculty of Biosciences and Medical Engineering, Universiti Teknologi Malaysia (UTM), Skudai, Johor 81310, Malaysia
*
Author to whom correspondence should be addressed.
Appl. Sci. 2016, 6(2), 40; https://doi.org/10.3390/app6020040
Submission received: 17 November 2015 / Revised: 16 December 2015 / Accepted: 5 January 2016 / Published: 1 February 2016
Browse Figures
Versions Notes

Abstract

:
To perform specific analysis for the single cell, individual cells have to be captured and separated from each other before further treatments and analysis can be carried out. This paper presents the design, simulation, fabrication, and testing of a microfluidic device for trapping a single cell/particle based on a hydrodynamic technique. A T-channel trapping chip has been proposed to provide single-cell trapping and consequently could be a platform for cell treatments and manipulations. A finite element T-channel trapping model was developed using Abaqus FEA™ software to observe it’s trapping ability by optimizing the channel’s geometry and RhMain/RhTrap ratio. A proof of concept demonstration for cell trapping in the T-channel model was presented in the simulation analysis and experimental work using HUVEC cell aggregate. The T-channel was found to be able to trap a single cell via the hydrodynamic trapping concept using an appropriate channel geometry and RhMain/RhTrap ratio. The proposed T-channel single-cell trapping has potential application for single cell characterization and single 3D cell aggregates treatments and analysis.

Graphical Abstract

1. Introduction

The focus of cell studies at the single cell level has emerged and expanded to further explore and understand the properties and specific responses of individual cells towards environmental conditions and treatment. Most of the methods available for cell analysis involve experiments performed in an array of culture media and treatments. The responses of single cells to the culture treatments are measured as the average response of a single cell population. Therefore, the heterogeneity of individual cells could be neglected, thus hiding the important signals or responses representing important individual or single cell properties. An individual manipulation platform is needed to perform analysis on a specific single cell. Previous single-cell mechanical and electrical characterization studies have been carried out by probing the single cells using an Atomic Force Microscopy (AFM) probe [1,2,3,4,5,6], the micropipette aspiration technique [7,8,9], a red blood cell (RBC) biomembrane probe [6,10,11], optical tweezers [6,12,13,14], and a microfluidic channel [15,16,17,18,19] to characterize single cell stiffness, adhesion, and electrical properties. AFM probe, micropipette aspiration, and biomembrane probe techniques require a single cell to be isolated and manipulated manually by a skilled operator using the micromanipulator system. The advancement of microfluidic technology has made single cell capturing possible by controlling the fluid flow. Additionally, the channels could be utilized as the individual platform for cell manipulations in microscale.
A variety of techniques have been employed to trap an individual cell within a microfluidic device. For example, microwell-based [20,21,22,23,24], dielectrophoresis-based [25,26,27,28,29], and hydrodynamic-based [30,31,32,33,34,35,36,37,38,39,40,41,42] microfluidic devices for single-cell trapping have been developed in response to an increasing demand for simple yet reliable tools for high-throughput cell manipulation at the single cell level. In microwell-based platforms, a precise geometry design is required to achieve high trapping efficiency [22]. Dielectrophoresis-based cell trapping applied a non-uniform AC field to manipulate polarized particles in suspension and is an effective technique to efficiently manipulate a single cell. However, this technique appears to damage the trapped cells, thus affecting the cell proliferation. Hydrodynamic trapping uses the altered fluidic resistance created by microstructures on a fluid path, such as sieve-like traps [41,42,43] or small trapping sites [30,31,32,33,34,35,44,45], to control the movement of cells in a microchannel. For straight or serpentine-shaped channels with trapping sites, the fluidic resistances of these channels are carefully calculated so that the fluid and cells in the main channel will be directed into the trapping sites when the channels are empty, but bypass them when they are occupied with a cell. The main challenge in hydrodynamic trapping is that it requires a precise microfluidic control of multiple streams and further investigation and optimization of cell trapping efficiencies are still required. Current microfluidic devices used for cell/3D cell culture face some drawbacks that limit their practical usage, such as the difficulty of accessing the trapped cells/3D cells in their trapping sites and the complexity of harvesting the cultured/treated cells for further analysis [46,47,48].
In this paper, we develop a T-channel single cell trap to capture a single cell and provide a platform for individual cell characterization. This T-channel provides a trapping site that allows for manipulation of a single cell using the trap channel’s outlet port via a syringe pump. Furthermore, the trapping site is not limited to the application of single cell study, but could be used for single 3D cell analysis for drug treatments, single spheroid tumor metastasis investigation, and protein study. A finite element T-channel trapping model was developed by designing and optimizing the channel’s geometry to produce an efficient single cell trapping system. The model is developed based on the hydrodynamic flow resistance (Rh) manipulation between the main channel and trap channel to achieve successful trapping. A proof of concept demonstration for cell trapping in the T-channel model is presented in the simulation analysis and experimental work using HUVEC cell aggregate. The developed finite element T-channel trapping model could be used for designing and optimizing the trapping of various types of cells of different sizes. Numerical simulations were carried out to evaluate the channel’s trapping efficiencies for different trap hole sizes and Rh of the main channel to Rh of the trap channel (RhMain/RhTrap) ratios. Cell aggregate trapping has been performed experimentally to support the simulation findings.

2. Idea and Concept

The available hydrodynamic trapping techniques inside a microfluidic chip have improved and enhanced research study involving cells, moving from the population batch experiment towards individual cell analysis. The trapping method has been widely used [30,31,32,33,34,35,44,45,49,50] as it enables high-throughput single cell trapping. However, currently available hydrodynamic trapping channels have limited capacity in providing a platform for individual cell manipulations for mechanical or electrical characterization. Realizing this need, researchers developed the idea to design T-channel single-cell trapping system with a microfluidic channel that could provide individual trapping site, thus enabling further single-cell characterization to be carried out. The T-channel trapping site is designed with two channels, a main and a trap channel. Figure 1 shows a schematic illustration of the hydrodynamic trapping concept with RhTrap and RhMain representing the flow resistance of the trap and the main channel, respectively. The RhTrap consists of the sum of three hydrodynamic resistances (RhT1+RhT2+RhT3). The yellow circle denotes a particle/cell to be trapped. For calculating the flow resistance of each channel, an analogous electrical circuit is considered, where the flow rate (Q) and the Rh are analogs of electric current and resistance, respectively. The main channel and trap channel’s length are represented by LMain and LTrap, respectively. WTrap and WHole are the trap channel’s and trap hole’s width, respectively. The flow rate of whole fluid at the inlet could be assumed as an electric current source. The outlets could be assumed as grounds because they are at atmospheric pressure. This T-channel is a unique trapping site that allows single-cell manipulation to be performed using the trap channel’s outlet port via a syringe pump.
Applsci 06 00040 g001 1024
Figure 1. Schematic illustration of single cell T-channel trapping model and the hydrodynamic resistance.
Figure 1. Schematic illustration of single cell T-channel trapping model and the hydrodynamic resistance.
Applsci 06 00040 g001
The hydrodynamic trapping concept can be summarized as follows: (a) the trapping channel has a lower Rh than the main channel when a trapping site is empty (Figure 2A); this will make the cells flow into the trapping stream and directed into the trap; (b) when a cell is trapped, it will act as a plug and increase the Rh along the trap channel (Figure 2B) drastically; and (c) the main flow will change from the trap channel to the bypass channel (main channel) and the next particles/cells will be directed to the bypass stream, passing by the filled trapping site [49].
The Darcy-Weisbach equation is used to determine the pressure drop or pressure difference in a microchannel to solve the continuity and momentum equations for the Hagen-Poiseuille flow problem. From the Hagen-Poiseuille equation, the flow rate (Q) can be defined by the following equation:
Δ P = Q × R h = Q × ( C μ L P 2 A 3 )
where ∆P is the pressure drop, Rh is the flow resistance of the rectangular channels, C is a constant that depends on the aspect ratio (ratio between height and width of the channel), μ is the fluid’s viscosity, and L, P, and A are the length, perimeter, and cross-sectional area of the channel, respectively.
Applsci 06 00040 g002 1024
Figure 2. Schematic illustration of the fluid’s hydrodynamic resistance in the microchannels for two different conditions; (A) empty trap channel (before cell trapping occurs); (B) after cells have been trapped.
Figure 2. Schematic illustration of the fluid’s hydrodynamic resistance in the microchannels for two different conditions; (A) empty trap channel (before cell trapping occurs); (B) after cells have been trapped.
Applsci 06 00040 g002
From Equation (1), by estimating that the pressure drop across the trap and the main channel are the same (∆PTrap = ∆PMain), the flow rate ratio (QTrap/QMain) or flow resistance ratio (RhMain/RhTrap) between the trap channel and the main channel can be given as follows [50]:
Q Trap Q Main = R h Main R h Trap = ( C Main C Trap ) ( L Main L Trap ) ( P Main P Trap ) 2 ( A Trap A Main ) 3
By using a relationship of A = W × H and P = 2 (W + H), where W and H are the width and height of the channel, respectively, Equation (2) can be defined as:
Q Trap Q Main = R h Main R h Trap = ( C Main C Trap ) ( L Main L Trap ) ( W Main + H Main W Trap + H Trap ) 2 ( W Trap H Trap W Main H Main ) 3
From Equations (2) and (3), it is noted that the flow rates of the trap channel (QTrap) and the main channel (QMain) are distributed depending on the corresponding Rh. For the trap to work, the flow rate along the trap channel must be greater than the main channel (QTrap > QMain). In other words, the flow resistance along the main channel must be greater than the trap channel (RhMain > RhTrap). Therefore, a single cell can be trapped by manipulating the flow resistance ratio (RhMain/RhTrap), which is determined by the geometric parameters of the channels.
A single-cell trapping model is developed to produce a finite element single-cell trapping system in which the optimization of a channel’s geometry and adjustment of desired cell size could be performed. The geometry of the trapping channel is a variable for optimization (see Equation (3)) and subject to the size of cells and the application that will be carried out in the channel after the cells are trapped. An example of a channel’s geometry optimization was presented in this paper using a 5-μm yeast cell model. For other cell sizes, some guidelines in designing and optimizing the cell trapping channel are discussed. Firstly the diameter of the viable cells/particle in suspension should be determined to estimate the range of suitable WHole sizes. The trap channel’s geometry size is dependent on the trapped cells’/particles’ applications. For example, if adherence cells are used and need to be cultured inside the trapping platform, the WTrap should be bigger than the diameter of the cell (viable cells in suspension before adhesion) because suspended cells will need space for cell adhesion, spreading and growing in time. In different applications, an individual ciliate protozoan, Tetrahymena thermophila [30], needs to be trapped and maintained in the trap channel for long-term monitoring of cell behavior. Therefore, no expansion in size is expected after the trapping process and the trap channel’s width does not require space for expansion. In summary, the geometry of channels is a variable (L, H, and W; see Equation (3)) for optimization, subject to the size, type and the application performed to the trapped cells.
For the T-channel single particle/cell trapping system, particles/cells are introduced into the device through the inlet with an appropriate flow rate and directed to the trap channel by optimizing the channel’s geometry. Trap hole and trap channel geometry are optimized and the main channel’s length (LMain) is manipulated to produce an appropriate Rh ratio that leads to successful trapping (see Equation (3)). The excess and remaining particles/cells will be directed out through the channel’s outlet by injecting the cell’s culture medium.

3. Methodology

3.1. Simulation Setup

Finite element analysis is carried out using ABAQUS-FEA™ (Dassault Systems, RI, USA). The single-cell trapping simulation model consists of fluid channels (the Eulerian part) and a yeast cell, modeled as a 3D deformable elastic sphere (Figure 3A,B). The fluid part was represented by two microchannels the main channel and the trap channel, which were modeled as a 3D Eulerian explicit EC3DR and an eight-node linear Eulerian brick, assigned with water properties (density, equation of state, and viscosity). The yeast cell was modeled as a sphere-shaped elastic 3D standard solid deformable C3D8R and an eight-node linear brick 3D part with yeast cell properties (Young’s modulus, Poisson’s ratio, and density) obtained from the literature [51,52,53,54,55,56,57]. The appropriate channel’s geometry to trap a 5μm, single-particle yeast cell in the specified design was studied. The finite element single-cell trapping model is focused on a single trap channel for geometry optimization due to the complexity and high processing time required for the analysis.
The parts assembly is demonstrated in Figure 3C, showing the initial position of the yeast cell before simulation. The fluid channel and yeast cell model were assembled to develop the single cell trapping model. The initial position of the yeast cell in the channel was fixed (the distance between the cell and the trap channel) throughout all simulations. The interaction for cell and water was defined as general contact with rough tangential behavior. Both the fluid channel and the cell were meshed using hexahedron mesh type and total mesh elements for the cell trapping model ranged from 28,043 to 100,803 elements. Eulerian boundary conditions applied to the channel’s wall were defined as no-inflow and non-reflecting outflow. A constant fluid inflow velocity of 1.0 μm·s−1 was applied to the inlet and the channel outlets were defined as free outflow.
The simulation analysis could be divided into two parts: T-channel single particle/cell trapping ability and the effects of different RhMain/RhTrap ratio and WHole. A T-channel model with a trap hole width of 3.0 μm was used to analyze trapping ability via a simulation analysis. To study the effects of RhMain/RhTrap ratio and WHole on cell trapping, various LMain values ranging from 50 to 580 μm and WHole values ranging from 1 to 5 were analyzed. The height of the main channel, trap channel, and trap hole were uniform (HChannel) at 7 μm throughout the analysis.
Applsci 06 00040 g003 1024
Figure 3. Development of a finite element model for a single-cell trapping system: (A) Eulerian part (fluid channel’s top view) represented by main channel and trap channel (T1 + T2 + T3); (B) 3D deformable part (yeast cell model); (C) parts assembly showing the initial position of cell before simulation.
Figure 3. Development of a finite element model for a single-cell trapping system: (A) Eulerian part (fluid channel’s top view) represented by main channel and trap channel (T1 + T2 + T3); (B) 3D deformable part (yeast cell model); (C) parts assembly showing the initial position of cell before simulation.
Applsci 06 00040 g003

3.2. Microfluidic Chip Fabrication

Microchannel design was transferred to the glass chrome mask by direct lithography. A 2.5-inch AZ-coated glass chrome mask AZP1350 (ULCOAT, Saitama, Japan) and a positive photoresist were exposed with the channel design in a mask aligner with ultraviolet (UV) power of 12 mW (μPGUV-N, Heidelberg Instruments, Heidelberg, Germany). The design-exposed masks were developed by dipping the masks into the chrome etchant for 1 min and rinsing them with deionized water (dH2O) to wash away the chrome etchant, followed by dipping into 70% ethanol for 1 min to remove the AZ layer. The chrome masks were further cleaned in 70% ethanol for 2 min in an ultrasonic cleaning machine. Six-inch-diameter silicon wafers were cleaned with dH2O and dried. The wafers (SUMCO Corp., Tokyo, Japan) were used as the substrate for mold development. SU8-3005 was spin coated onto the wafers at 5000 rpm for 10 s to get a thickness of 15 μm followed a reduced spin speed at 1000 rpm for 30 s. The SU8-coated silicon wafers were soft baked at 95 °C for 10 min. The wafers were then exposed to UV light (μPGUV-N, Heidelberg Instruments, Heidelberg, Germany) using a mask aligner for 8 s at 200 mJ/cm, post-baked at 95 °C for 6 min, developed using SU8 developer for 6 min, dipped into fresh SU8 developer, and dried using an air blower. The developed microchannel pattern was then used as a mold to develop the microfluidic devices. The polymethylsiloxane (PDMS) (Dow corning, Midland, MI, USA) microfluidic devices are fabricated by replica molding using the patterned silicon wafer. PDMS prepolymer and a curing agent were mixed in the ratio of 9:1, degassed, poured on the patterned-channel mold inside 10 cm petri dishes, and cured in a convection oven at 65 °C for 2 h to complete the cross-linking. The cured PDMS was peeled from the mold and cut into individual devices. The holes for inlets and outlets were punched with a hollow needle 1 mm in diameter. Plasma oxidation (20 mA, 3 min) was used to activate the surfaces of PDMS and glass slides, followed by heating on a hot plate at 95 °C for 1 h to seal the PDMS and glass. Figure 4 shows a summary of the microchip fabrication steps.
Applsci 06 00040 g004 1024
Figure 4. Fabrication steps for the development of (A) microchannel mask; (B) mold or microchannel pattern; (C) PDMS channel; (D) microchip assembly.
Figure 4. Fabrication steps for the development of (A) microchannel mask; (B) mold or microchannel pattern; (C) PDMS channel; (D) microchip assembly.
Applsci 06 00040 g004

3.3. Cell Culture and Cell Aggregates Formation

HUVECs (frozen stock) were commercially obtained from Clonetics (Cambrex, Inc., Walkersville, MD, USA). Cells were defrosted, thawed, and grown in endothelial growth medium (EGM-2 BulletKit, Lonza, Basel, Switzerland) supplemented with 2% fetal bovine serum, antibiotics (gentamicin sulfate/amphotericin B), 0.4% human fibroblast growth factor-B, 0.04% hydrocortisone, 0.1% human epidermal growth factor, ascorbic acid, heparin, vascular endothelial growth factor, and insulin-like growth factor (R3-IGF-1). Cultures were maintained at 37 °C in a humidified atmosphere with 5% CO2. Media were changed at 24 h after thawing and every 48 h onwards. When the cultures reached 80%–90% confluence, cells were subcultured and washed with phosphate-buffered saline (PBS) and detached using 1 mL of trypsin-EDTA. Once cells were detached, the trypsin effect was neutralized with 2 mL of EGM-2 medium and cells were centrifuged at 220× g for 5 min at 25 °C. Cells were seeded at a minimum density of 103 cells/cm2 in culture flasks or plates. For cell aggregates formation, 1 × 106 HUVEC cells in passage 10 were harvested by centrifugation and re-suspended with 1 mL EGM-2 medium in 15-mL prolypropylene centrifuge tubes. Cells were incubated for 1 h and the tubes’ caps were loosened to allow oxygen supply to the cells during culture/incubation. Cell aggregates with diameter in the range of 30–60 μm formed spontaneously during incubation.

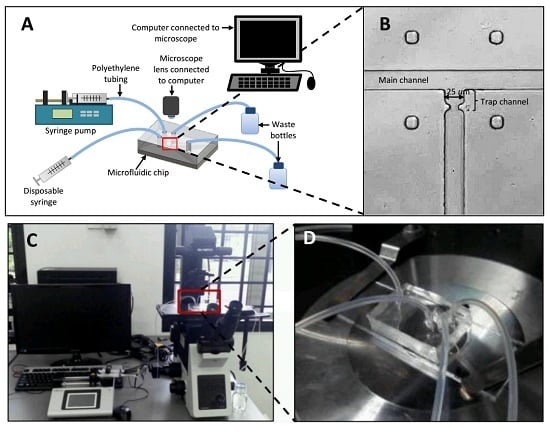
3.4. Experimental Setup

The microfluidic chip consists of two inlets (medium and cell aggregates suspension) and two outlets (from the trap channel and the main channel) with the T-channel trapping site positioned in the middle of the microchip (Figure 5B). The inlets were connected to 1 mm diameter polyethylene tubing as inlets and outlet ports, for fluid and cell aggregates injection and withdrawal (Figure 5A,D). The length of polyethylene tubing for both outlets should be the same to ensure the appropriate RhMain/RhTrap of both the main and the trap channel. The tubing for the outlets was connected to the waste reservoir (Figure 5A,C). A microfluidic chip was connected through the inlets to legato 180 syringe pumps (KD Scientific™, Holliston, MA, USA) equipped with 3-mL disposable syringes (Terumo Medical Corp., Tokyo, Japan). The chip was perfused with EGM-2 medium (Lonza, Walkersville, MD, USA) through inlet 1 at a flow rate 50 μL/min to remove air bubbles and the flow was reduced to 10 μL/min for subsequent analyses. Cell aggregates suspensions were diluted to 10 cells per μm medium before being injected into the microfluidic chip at the flow rate of 50 μL/min. The cell aggregates were monitored in real time, using inverted microscope IX71 (Olympus, Tokyo Japan) with 40× magnification.
Applsci 06 00040 g005 1024
Figure 5. (A) Schematic diagram of the experimental setup; (B) a close-up image of the trapping channel; (C) experimental setup; (D) a close-up real image of the T channel microfluidic chip positioned under the inverted microscope.
Figure 5. (A) Schematic diagram of the experimental setup; (B) a close-up image of the trapping channel; (C) experimental setup; (D) a close-up real image of the T channel microfluidic chip positioned under the inverted microscope.
Applsci 06 00040 g005

4. Results and Discussions

4.1. T-Channel Trapping Ability

The finite element model for the T-channel trapping was developed to evaluate the channel’s ability to trap single cells depending on the desired cell size. The model was designed to have two outlets that lead to the waste reservoir and to be operated by fluid infusion through the inlets. In the simulation analyses, the T-channel trapping model was developed to trap a 5-μm yeast cell. A T-channel trapping model with a trap hole width (WHole) of 3.0 μm was used to observe the appropriate flow resistance ratio of the main channel to the trap channel (RhMain/RhTrap) for single particle/cell trapping. The main channel’s length (LMain) was manipulated to create an RhMain/RhTrap ratio ranging from 0.5 to 5. Increasing the RhMain/RhTrap ratio is proportional with the increase in the main channel’s (main path) length. Figure 6 represents the result of cell trapping for a model with an RhMain/RhTrap ratio ranging from 1 to 6 at the 25 s point of the simulation time. A yeast cell model was trapped when a RhMain/RhTrap ratio of 2 or higher was used with various cell positions in the trap channel during a simulation time of 25 s (Figure 6B–E). A higher RhMain/RhTrap ratio produced faster cell trapping. Models with an RhMain/RhTrap ratio of 1 or less were not able to trap the cell, causing the cell to bypass the trap channel to enter the main channel (Figure 6A).
The simulation results show that an RhMain/RhTrap ratio of 2 or above is able to trap single cells using the hydrodynamic trapping concept. The fluid’s velocity inside the main channel and trap channel were further investigated to analyze the fluid’s velocity profile in the channels before and after cell trapping occurred. A T-channel model with a WHole 3 and RhMain/RhTrap ratio of 3 was chosen for the analysis. Figure 7A represents the fluid’s velocity position in the trap and main channel and the graph in Figure 7B presents the fluid’s velocity measurement in the trap and main channel before and after trapping. Before cell trapping occurred, the fluid’s velocity inside the trap was higher than in the main channel; conversely, after the cell was trapped, the fluid’s velocity inside the trap channel decreased dramatically while the fluid’s velocity in the main channel increased instantly. When the velocity of fluid in the trap channel is higher than the main, it leads to a lower hydrodynamic resistance in the trapping site, which creates a trapping stream directing the cell into the trap channel. further blocks the trap hole and drastically decreases the fluid’s velocity inside the trap channel. This finding supports the principle of hydrodynamic trapping in which, when the trapping site is empty, the trap channel will have lower flow resistance compared to the main channel. The direction of fluid flow diverges from the trap channel to the main path (main channel); therefore, subsequent cells will be directed to the main path. These findings were supported by the simulation outcome using three cells and a T-channel model with an RhMain/RhTrap ratio of 3 and a WHole width of 3 μm. The analyses were carried out to investigate the movement of subsequent cells after trapping occurred. Results obtained show that the first cell moved into the trap channel (Figure 8B) and subsequent cells bypassed the trap channel (Figure 8C). The velocity streamlines plots illustrate how the fluid stream was directed to the trap channel during cell trapping (Figure 8B) but the direction changed to the main channel after the cell trapping (Figure 2C). Subsequent analysis showed the effects of RhMain/RhTrap in the T-channel trapping.
Applsci 06 00040 g006 1024
Figure 6. Model’s trapping ability at different RhMain/RhTrap ratios ranging from (A) 1; (B) 2; (C) 3; (D) 4; (E) 5; (F) 6.
Figure 6. Model’s trapping ability at different RhMain/RhTrap ratios ranging from (A) 1; (B) 2; (C) 3; (D) 4; (E) 5; (F) 6.
Applsci 06 00040 g006
Applsci 06 00040 g007 1024
Figure 7. (A) Points representing velocity of fluid in the trap channel (left side) and main channel (right side); (B) graph representing velocity of fluid in trap channel and main channel for T-channel trapping model with RhMain/RhTrap ratio of 3.0 before and after cell trapping.
Figure 7. (A) Points representing velocity of fluid in the trap channel (left side) and main channel (right side); (B) graph representing velocity of fluid in trap channel and main channel for T-channel trapping model with RhMain/RhTrap ratio of 3.0 before and after cell trapping.
Applsci 06 00040 g007
Applsci 06 00040 g008 1024
Figure 8. Simulation findings of fluid’s velocity streamline plots for model with WHole of 3 µm and RhMain/RhTrap ratio of 3 during: (A) the initial position of cells; (B) cell trapping; and (C) after cell trapping.
Figure 8. Simulation findings of fluid’s velocity streamline plots for model with WHole of 3 µm and RhMain/RhTrap ratio of 3 during: (A) the initial position of cells; (B) cell trapping; and (C) after cell trapping.
Applsci 06 00040 g008

4.2. Effects of Different RhMain/RhTrap Ratio and WHole

Further simulation analyses were carried out to examine the effects of different RhMain/RhTrap ratios ranging from 0.5 to 5.0 on the T-channel trapping with a WHole of 3 μm. LMain was manipulated to comply with the desired RhMain/RhTrap ratio. The hydrodynamic trapping concept was found to work accordingly for a T-channel with an RhMain/RhTrap ratio of 2.0 and above as the yeast cell model was directed into the trap channel by the fluid stream and trapped in the trap channel (Figure 9 and Figure 10). The fluid velocity profile and streamline field of the cell trapping model were analyzed to understand the hydrodynamic trapping mechanism. Fluid velocity streamlines presented the direction where the fluid stream was heading, while velocity profiles represented the velocity value in the channel by the contour color. The velocity streamlines produced by the cell trapping model with an RhMain/RhTrap ratio of 1.0 and less were found to deviate from most of the streamlines headed to the main channel instead of the trap channel (Figure 9A). Therefore, the stream was unable to lead the cell into the trap channel. This finding is in agreement with the fluid’s velocity distribution produced by the same model (Figure 10A). Results show that the main channel’s fluid velocity for the single-cell trapping model with an RhMain/RhTrap ratio of 1.0 was higher compared to the trap channel’s fluid velocity. Therefore the fluid stream will direct the yeast cell to flow into the main channel’s path and bypass the trap channel.
In contrast with the cell trapping model with an RhMain/RhTrap ratio of 2.0 and above (Figure 9B–D), the streamline profiles show the fluid flow diverging from the main channel into the trap channel; most streamlines were directed towards the trap channel. For models with an RhMain/RhTrap ratio of 2.0 (Figure 10B–D), the fluid’s velocity in the trap hole was higher compared to the fluid’s velocity in the main channel. These results show that the trap channel produces lower hydrodynamic resistance than the main channel and the mainstream will direct the yeast cell into the trap channel. Models with an RhMain/RhTrap ratio of 2.0–4.0 (Figure 10B–D) had similar fluid velocity patterns to provide an appropriate pressure drop for cell trapping. However, there are variations found in cell trapping time between different RhMain/RhTrap ratios. A higher RhMain/RhTrap ratio requires a shorter time for the trapping process compared to a lower ratio. The graph in Figure 11 shows the results of trapping time for cell trapping models with a WHole of 3.0 and an RhMain/RhTrap ratio ranging from 1.0 to 6.0. The graph shows that the trapping time decreases with increasing RhMain/RhTrap. This was probably due to a higher RhMain/RhTrap ratio that enables velocity distribution in a shorter time compared to the lower RhMain/RhTrap. A greater RhMain/RhTrap ratio could produce lower hydrodynamic resistance in the trap channel and could transfer the fluid at a faster rate [58,59]. The velocity distribution produced different pressure inside the main channel and trap channel, causing the fluid’s stream to be directed to the trap channel and bringing the cell into a lower flow resistance area for trapping.
Applsci 06 00040 g009 1024
Figure 9. Velocity streamlines before cell trapping (top view) for cell trapping model with a WHole of 3 μm for different RhMain/RhTrap ratios of (A) 1.0; (B) 2.0; (C) 3.0; and (D) 4.0. V represents the fluid’s velocity in μm·s−1.
Figure 9. Velocity streamlines before cell trapping (top view) for cell trapping model with a WHole of 3 μm for different RhMain/RhTrap ratios of (A) 1.0; (B) 2.0; (C) 3.0; and (D) 4.0. V represents the fluid’s velocity in μm·s−1.
Applsci 06 00040 g009
Applsci 06 00040 g010 1024
Figure 10. Velocity of fluid before cell trapping for single-cell trapping model with a WHole width of 3 μm for RhMain/RhTrap ratios of of (A) 1.0; (B) 2.0; (C) 3.0; and (D) 4.0. V represents the fluid’s velocity in μm·s−1.
Figure 10. Velocity of fluid before cell trapping for single-cell trapping model with a WHole width of 3 μm for RhMain/RhTrap ratios of of (A) 1.0; (B) 2.0; (C) 3.0; and (D) 4.0. V represents the fluid’s velocity in μm·s−1.
Applsci 06 00040 g010
Applsci 06 00040 g011 1024
Figure 11. Cell trapping time for model with different RhMain/RhTrap ranging from 1.0 to 6.0 for T-channel trapping model with a WHole of 3 μm.
Figure 11. Cell trapping time for model with different RhMain/RhTrap ranging from 1.0 to 6.0 for T-channel trapping model with a WHole of 3 μm.
Applsci 06 00040 g011
Simulation analyses were undertaken to observe the effects of WHole in the T-channel model’s trapping ability. A T-channel model with WHole values ranging from 1.0 to 5.0 was examined with different RhMain/RhTrap ratios between 2.0 and 6.0. For T-channel trapping models with a WHole width of 2.0 μm or less, the cell was unable to be trapped and bypassed the trap channel to enter the main channel. The velocity streamlines produced show that the fluid stream was not fully focused into the trap channel (Figure 12A). Additionally, the fluid’s velocity in the present main channel was high (Figure 13A) compared to the models with a WHole of 2μm and above (Figure 13B–D). The high fluid stream in the main channel directed cells to bypass the trap channel and prevented cell trapping from occurring (Figure 13A). This result shows that a WHole of 2 μm or less is not suitable for the specified trap channel dimension (7 μm width, height, and length). The small WHole probably caused a very low fluid velocity distribution and produced a pressure drop that prevented cells’ movement into the trap channel [28]. The hydrodynamic trapping concept is found to be ineffective for a cell trapping model with a WHole of 2.0 μm or less. A simulation study performed by Khalili et al. [59] showed the same trend when a very small WHole/WTrap value was used. However, for a T-channel model with a WHole of 3 μm or higher, the yeast cell model was directed into the trap channel (Figure 12 and Figure 13). The streamlines produced were focused in the direction of the trap channel (Figure 12B–D) and the fluid’s velocity was found to be higher in the trap compared to the main channel (Figure 13B–D). A bigger WHole value was found to produce higher fluid velocity inside the trap channel (Figure 13B–D) and required shorter trapping time compared to the smaller WHole (data not shown). Table 1 summarizes the simulation findings for a single-cell trapping model’s ability at different values of WHole and various RhMain/RhTrap ratios. The T-channel trapping model was able to perform cell trapping when WHole values of 3 μm and higher were used with an RhMain/RhTrap ratio of 2 and above.
Applsci 06 00040 g012 1024
Figure 12. Velocity streamlines before cell trapping (top view) for a cell trapping model with RhMain/RhTrap ratios of 3 for different WHole of (A) 2 μm; (B) 3 μm; (C) 4 μm; and (D) 5 μm. V represents the fluid’s velocity in μm·s−1.
Figure 12. Velocity streamlines before cell trapping (top view) for a cell trapping model with RhMain/RhTrap ratios of 3 for different WHole of (A) 2 μm; (B) 3 μm; (C) 4 μm; and (D) 5 μm. V represents the fluid’s velocity in μm·s−1.
Applsci 06 00040 g012
Applsci 06 00040 g013 1024
Figure 13. Velocity of fluid before cell trapping for a single-cell trapping model with RhMain/RhTrap ratios of 3 for different WHole of (A) 2 μm; (B) 3 μm; (C) 4 μm; and (D) 5 μm. V represents the fluid’s velocity in μm·s−1.
Figure 13. Velocity of fluid before cell trapping for a single-cell trapping model with RhMain/RhTrap ratios of 3 for different WHole of (A) 2 μm; (B) 3 μm; (C) 4 μm; and (D) 5 μm. V represents the fluid’s velocity in μm·s−1.
Applsci 06 00040 g013
Table
Table 1. Summary of the simulation results for a single-cell trapping model’s ability for different values of WHole and various RhMain/RhTrap ratios.
Table 1. Summary of the simulation results for a single-cell trapping model’s ability for different values of WHole and various RhMain/RhTrap ratios.
WHole/RhMain/RhTrap Ratio1.0 µm1.5 µm2.0 µm2.5 µm3.0 µm3.5 µm4.0 µm4.5 µm5.0 µm
0.5nonononononononono
1.0nonononononononono
1.5nonononoyesyesyesyesyes
2.0nonononoyesyesyesyesyes
2.5nonononoyesyesyesyesyes
3.0nonononoyesyesyesyesyes
3.5nonononoyesyesyesyesyes
4.0nonononoyesyesyesyesyes
4.5nonononoyesyesyesyesyes
5.0nonononoyesyesyesyesyes
5.5nonononoyesyesyesyesyes
6.0nonononoyesyesyesyesyes

4.3. Experimental Verification

After analyzing the T-channel’s trapping ability by simulation, five microchips were fabricated with a trap channel size appropriate to trap a cell aggregate with a diameter of 25–35 μm. The trap channel’s size was designed to be WTrap 25 μm, WHole 15 μm, LTrap 25 μm, and HChannel 15 μm with an RhMain/RhTrap ratio of 3. The computational prediction for - channel trapping was further validated experimentally using fabricated microfluidic devices and HUVEC cell aggregates. A single HUVEC cell aggregate was found to be directed by the fluid flow to enter the trap channel and trapped. Consistent results were obtained using all five fabricated microchips. Figure 14A–F demonstrate the movement of cell aggregates inside the T-channel from the channel’s inlet (right side) before and after trapping, sequentially. The single-cell aggregate moved from the inlet into the main channel (Figure 14A), reached the junction between the trap and main path (Figure 14B), entered the trap channel (Figure 14C), and was captured in the trap channel (Figure 14D). Results show that the fluid stream produced inside the T-channel was able to direct and lead the cell aggregate to enter the trap channel. In addition, the subsequent cell aggregate moved to bypass the trap channel (Figure 14E) and passed through the main channel (Figure 14F). This finding demonstrated that a change of hydrodynamic resistance between the channels occurred after the cell aggregate was trapped. This caused the increase of RhTrap and prevented subsequent cell aggregates from entering the trap channel. This result was in agreement with the simulation data and hydrodynamic trapping concept. This T-channel trapping could be applied to trapping other cell types and sizes. For example, for the purpose of trapping a smaller single cell, WTrap, WHole, LTrap, and HChannel dimensions should be reduced, while for single spheroid capture, the dimension should be increased appropriately for the target cell.
The proposed T-channel trapping is an approach to trap a single cell with a platform for single-cell analysis plus access for further manipulation through the WHole and its outlet. This T-channel could be upgraded by increasing its throughput ability through applying more parallel trapping channels in a single microfluidic chip. Therefore, many single cells/3D cells could be cultured and applied with treatments at a time. The treated cells/3D cells could be further analyzed by applying mechanical or electrical characterization (e.g., stiffness, adhesion, or electrical measurements) in the manipulation platform and can be harvested from the microfluidic chip for further analysis.
Applsci 06 00040 g014 1024
Figure 14. Experimental results using a fabricated T-channel chip demonstrating the sequential of HUVEC cell aggregate trapping: (A) cell aggregate movement from inlet to the main channel; (B) cell aggregate before reaching trap channel; (C) cell aggregate movement into trap channel; (D) cell aggregate trapped into trap channel; (E) subsequent cell aggregate approaching trap channel; (F) subsequent cell aggregate bypassed trap channel.
Figure 14. Experimental results using a fabricated T-channel chip demonstrating the sequential of HUVEC cell aggregate trapping: (A) cell aggregate movement from inlet to the main channel; (B) cell aggregate before reaching trap channel; (C) cell aggregate movement into trap channel; (D) cell aggregate trapped into trap channel; (E) subsequent cell aggregate approaching trap channel; (F) subsequent cell aggregate bypassed trap channel.
Applsci 06 00040 g014

5. Conclusions

This study presents a T-channel single particle/cell hydrodynamic trap that provides a platform and access for further single particle/cell characterization. The channel has a unique trapping site that allows for single particle/cell manipulation to be performed using the trap channel’s outlet port. A finite element T-channel trapping model has been developed and could be utilized as a guideline in designing T-channel trapping for other cell/particle types and sizes for microchip fabrication. Trapping ability can be simulated and analyzed using the developed finite element T-channel trapping model and has been validated by experiment using HUVEC cell aggregates. The proposed T-channel has potential applications in single-cell characterization, single 3D cell aggregates drugs treatments, and spheroid tumor and metastasis studies.

Acknowledgments

The research was supported by the Ministry of Higher Education of Malaysia (grant Nos. 4L640 and 4F351) and Universiti Teknologi Malaysia (grant Nos. 4J148, 02G46, 03H82, and 03H80); we thank them for funding this project and for their endless support. The authors would like to express their heartiest appreciation to Mohd Ariffanan Mohd Basri from the Faculty of Electrical Engineering, Universiti Teknologi Malaysia for his contribution of ideas and valuable discussion during the theoretical development of this study.

Author Contributions

Amelia Ahmad Khalili, designed and performed the experiments and Mohd Ridzuan Ahmad supervised the project and edited the article. Masaru Takeuchi, Masahiro Nakajima, and Yasuhisa Hasegawa contributed to the reagents, materials and microchip fabrication facilities. Razauden Mohamed Zulkifli contributed to the cells, reagents, and materials for the experimental studies.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hoffmann, C.S.; Cohnen, A.; Ludwig, T.; Watzl, C. 2B4 engagement mediates rapid LFA-1 and actin-dependent NK cell adhesion to tumor cells as measured by single cell force spectroscopy. J. Immunol. 2011, 186, 2757–2764. [Google Scholar] [CrossRef] [PubMed]
  2. Beaussart, A.; El-Kirat-Chatel, S.; Sullan, R.M.A.; Alsteens, D.; Herman, P.; Derclaye, S.; Dufrêne, F.Y. Quantifying the forces guiding microbial cell adhesion using single-cell force spectroscopy. Nat. Protoc. 2014, 9, 1049–1055. [Google Scholar] [CrossRef] [PubMed]
  3. Engel, A.; Gaub, E.H. Structure and mechanics of membrane proteins. Annu. Rev. Biochem. 2008, 77, 127–148. [Google Scholar] [CrossRef] [PubMed]
  4. Yang, S.-P.; Yang, C.-Y.; Lee, T.-M.; Lui, T.-S. Effects of calcium-phosphate topography on osteoblast mechanobiology determined using a cytodetacher. Mater. Sci. Eng. C 2012, 32, 254–262. [Google Scholar] [CrossRef]
  5. Muller, J.D. AFM: A Nanotool in Membrane Biology. Biochemistry 2008, 47, 7896–7898. [Google Scholar] [CrossRef] [PubMed]
  6. Khalili, A.A.; Ahmad, R.M. A review of cell adhesion studies for biomedical and biological applications. Int. J. Mol. Sci. 2015, 16, 18149–18184. [Google Scholar] [CrossRef] [PubMed]
  7. Palmer, C.P.; Mycielska, M.E.; Burcu, H.; Osman, K.; Collins, T.; Beckerman, R.; Perrett, R.; Johnson, H.; Aydar, E.; Djamgoz, M.B.A. Single cell adhesion measuring apparatus (SCAMA): Application to cancer cell lines of different metastatic potential and voltage-gated Na+ channel expression. Eur. Biophys. J. 2008, 37, 359–368. [Google Scholar] [CrossRef] [PubMed]
  8. Gao, Z.; Wang, S.; Zhu, H.; Su, C.; Xu, G.; Lian, X. Using selected uniform cells in round shape with a micropipette to measure cell adhesion strength on silk fibroin-based materials. Mater. Sci. Eng. C 2008, 28, 1227–1235. [Google Scholar] [CrossRef]
  9. Hochmuth, R.M. Micropipette aspiration of living cells. J. Biomech. 2000, 33, 15–22. [Google Scholar] [CrossRef]
  10. Gourier, C.; Jegou, A.; Husson, J.; Pincet, F. A nanospring named erythrocyte. The biomembrane force probe. Cell. Mol. Bioeng. 2008, 1, 263–275. [Google Scholar] [CrossRef]
  11. Evans, E.; Heinrich, V.; Leung, A.; Kinoshita, K. Nano- to microscale dynamics of P-selectin detachment from leukocyte interfaces. I. Membrane separation from the cytoskeleton. Biophys. J. 2005, 88, 2288–2298. [Google Scholar] [CrossRef] [PubMed]
  12. Castelain, M.; Rouxhet, P.G.; Pignon, F.; Magnin, A.; Piau, J.-M. Single-cell adhesion probed in-situ using optical tweezers: A case study with Saccharomyces cerevisiae. J. Appl. Phys. 2012, 111. [Google Scholar] [CrossRef]
  13. Schwingel, M.; Bastmeyer, M. Force mapping during the formation and maturation of cell adhesion sites with multiple optical tweezers. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
  14. Castelain, M.; Pignon, F.; Piau, J.-M.; Magnin, A. The initial single yeast cell adhesion on glass via optical trapping and Derjaguin-Landau-Verwey-Overbeek predictions. J. Chem. Phys. 2008, 128. [Google Scholar] [CrossRef] [PubMed]
  15. Chen, J.; Zheng, Y.; Tan, Q.; Zhang, Y.L.; Li, J.; Geddie, W.R.; Jewett, M.A.S.; Sun, Y. A microfluidic device for simultaneous electrical and mechanical measurements on single cells. Biomicrofluidics 2011, 5. [Google Scholar] [CrossRef] [PubMed]
  16. Mondal, D.; RoyChaudhuri, C.; Das, L.; Chatterjee, J. Microtrap electrode devices for single cell trapping and impedance measurement. Biomed. Microdevices 2012, 14, 955–964. [Google Scholar] [CrossRef] [PubMed]
  17. Gabriele, S.; Versaevel, M.; Preira, P.; Theodoly, O. A simple microfluidic method to select, isolate, and manipulate single-cells in mechanical and biochemical assays. Lab Chip 2010, 10, 1459–1467. [Google Scholar] [CrossRef] [PubMed]
  18. Forsyth, A.M.; Wan, J.; Ristenpart, W.D.; Stone, H.A. The dynamic behavior of chemically “stiffened” red blood cells in microchannel flows. Microvasc. Res. 2010, 80, 37–43. [Google Scholar] [CrossRef] [PubMed]
  19. Cho, Y.; Kim, H.S.; Bruno Frazier, A.; Chen, Z.G.; Shin, D.M.; Han, A. Whole-cell impedance analysis for highly and poorly metastatic cancer cells. J. Microelectromech. Syst. 2009, 18, 808–817. [Google Scholar]
  20. Lee, G.-H.; Kim, S.-H.; Kang, A.; Takayama, S.; Lee, S.-H.; Park, J.Y. Deformable L-shaped microwell array for trapping pairs of heterogeneous cells. J. Micromech. Microeng. 2015, 25. [Google Scholar] [CrossRef]
  21. Sun, T.; Kovac, J.; Voldman, J. Image-based single-cell sorting via dual-photopolymerized microwell arrays. Anal. Chem. 2014, 86, 977–981. [Google Scholar] [CrossRef] [PubMed]
  22. Rettig, J.R.; Folch, A. Large-scale single-cell trapping and imaging using microwell arrays. Anal. Chem. 2005, 77, 5628–5634. [Google Scholar] [CrossRef] [PubMed]
  23. Tang, J.; Peng, R.; Ding, J. The regulation of stem cell differentiation by cell-cell contact on micropatterned material surfaces. Biomaterials 2010, 31, 2470–2476. [Google Scholar] [CrossRef] [PubMed]
  24. Doh, J.; Kim, M.; Krummel, M.F. Cell-laden microwells for the study of multicellularity in lymphocyte fate decisions. Biomaterials 2010, 31, 3422–3428. [Google Scholar] [CrossRef] [PubMed]
  25. Chen, N.-C.; Chen, C.-H.; Chen, M.-K.; Jang, L.-S.; Wang, M.-H. Single-cell trapping and impedance measurement utilizing dielectrophoresis in a parallel-plate microfluidic device. Sens. Actuators B Chem. 2014, 190, 570–577. [Google Scholar] [CrossRef]
  26. Sen, M.; Ino, K.; Ramon-Azcon, J.; Shiku, H.; Matsue, T. Cell pairing using a dielectrophoresis-based device with interdigitated array electrodes. Lab Chip 2013, 13, 3650–3652. [Google Scholar] [CrossRef] [PubMed]
  27. Voldman, J.; Gray, M.L.; Toner, M.; Schmidt, M.A. A microfabrication-based dynamic array cytometer. Anal. Chem. 2002, 74, 3984–3990. [Google Scholar] [CrossRef] [PubMed]
  28. Thomas, R.S.; Morgan, H.; Green, N.G. Negative DEP traps for single cell immobilisation. Lab Chip 2009, 9, 1534–1540. [Google Scholar] [CrossRef]
  29. Gray, D.S.; Tan, J.L.; Voldman, J.; Chen, C.S. Dielectrophoretic registration of living cells to a microelectrode array. Biosens. Bioelectron. 2004, 19, 771–780. [Google Scholar] [CrossRef] [PubMed]
  30. Chen, Y.-C.; Allen, S.G.; Ingram, P.N.; Buckanovich, R.; Merajver, S.D.; Yoon, E. Single-cell migration chip for chemotaxis-based microfluidic selection of heterogeneous cell populations. Sci. Rep. 2015, 5, 1–13. [Google Scholar] [CrossRef] [PubMed]
  31. Jin, D.; Deng, B.; Li, J.X.; Cai, W.; Tu, L.; Chen, J.; Wu, Q.; Wang, W.H. A microfluidic device enabling high-efficiency single cell trapping. Biomicrofluidics 2015, 9. [Google Scholar] [CrossRef] [PubMed]
  32. Benavente-Babace, A.; Gallego-Pérez, D.; Hansford, D.J.; Arana, S.; Pérez-Lorenzo, E.; Mujika, M. Single-cell trapping and selective treatment via co-flow within a microfluidic platform. Biosens. Bioelectron. 2014, 61, 298–305. [Google Scholar] [CrossRef] [PubMed]
  33. Kim, J.; Erath, J.; Rodriguez, A.; Yang, C. A high-efficiency microfluidic device for size-selective trapping and sorting. Lab Chip 2014, 14, 2480–2490. [Google Scholar] [CrossRef] [PubMed]
  34. Lee, P.J.; Hung, P.J.; Shaw, R.; Jan, L.; Lee, L.P. Microfluidic application-specific integrated device for monitoring direct cell-cell communication via gap junctions between individual cell pairs. Appl. Phys. Lett. 2005, 86. [Google Scholar] [CrossRef]
  35. Frimat, J.-P.; Becker, M.; Chiang, Y.-Y.; Marggraf, U.; Janasek, D.; Hengstler, J.G.; Franzke, J.; West, J. A microfluidic array with cellular valving for single cell co-culture. Lab Chip 2011, 11, 231–237. [Google Scholar] [CrossRef] [PubMed]
  36. Kim, H.; Lee, S.; Kim, J. Hydrodynamic trap-and-release of single particles using dual-function elastomeric valves: design, fabrication, characterization. Microfluid. Nanofluid. 2012, 13, 835–844. [Google Scholar] [CrossRef]
  37. Arakawa, T.; Noguchi, M.; Sumitomo, K.; Yamaguchi, Y.; Shoji, S. High-throughput single-cell manipulation system for a large number of target cells. Biomicrofluidics 2011, 5. [Google Scholar] [CrossRef] [PubMed]
  38. Kobel, S.; Valero, A.; Latt, J.; Renaud, P.; Lutolf, M. Optimization of microfluidic single cell trapping for long-term on-chip culture. Lab Chip 2010, 10, 857–863. [Google Scholar] [CrossRef] [PubMed]
  39. Hong, S.; Pan, Q.; Lee, L.P. Single-cell level co-culture platform for intercellular communication. Integr. Biol. 2012, 4, 374–380. [Google Scholar] [CrossRef] [PubMed]
  40. Shi, W.; Qin, J.; Ye, N.; Lin, B. Droplet-based microfluidic system for individual Caenorhabditis elegans assay. Lab Chip 2008, 8, 1432–1435. [Google Scholar] [CrossRef] [PubMed]
  41. Di Carlo, D.; Aghdam, N.; Lee, L.P. Single-cell enzyme concentrations, kinetics, and inhibition analysis using high-density hydrodynamic cell isolation arrays. Anal. Chem. 2006, 78, 4925–4930. [Google Scholar] [CrossRef] [PubMed]
  42. Skelley, A.M.; Kirak, O.; Suh, H.; Jaenisch, R.; Voldman, J. Microfluidic control of cell pairing and fusion. Nat. Meth. 2009, 6, 147–152. [Google Scholar] [CrossRef] [PubMed]
  43. Di Carlo, D.; Wu, L.Y.; Lee, L.P. Dynamic single cell culture array. Lab Chip 2006, 6, 1445–1449. [Google Scholar] [CrossRef] [PubMed]
  44. Tan, W.-H.; Takeuchi, S. A trap-and-release integrated microfluidic system for dynamic microarray applications. Proc. Natl. Acad. Sci. USA 2007, 104, 1146–1151. [Google Scholar] [CrossRef] [PubMed]
  45. Chung, K.; Rivet, C.A.; Kemp, M.L.; Lu, H.; States, U. Imaging single-cell signaling dynamics with a deterministic high-density single-cell trap array. Anal. Chem. 2011, 83, 7044–7052. [Google Scholar] [CrossRef] [PubMed]
  46. Jin, H.-J.; Cho, Y.-H.; Gu, J.-M.; Kim, J.; Oh, Y.-S. A multicellular spheroid formation and extraction chip using removable cell trapping barriers. Lab Chip 2011, 11, 115–119. [Google Scholar] [CrossRef] [PubMed]
  47. Kangsun, L.; Choong, K.; Jae, Y.Y.; Hun, L.; Byungwook, A.; Linfeng, X.; Ji, Y.K.; Oh, K.W. Gravity-oriented microfluidic device for uniform and massive cell spheroid formation. Biomicrofluidics 2012, 6, 14114–141147. [Google Scholar]
  48. Li, X.; Valadez, A.V.; Zuo, P.; Nie, Z. Microfluidic 3D cell culture: potential application for tissue-based bioassays. Bioanalysis 2012, 4, 1509–1525. [Google Scholar] [CrossRef] [PubMed]
  49. Teshima, T.; Ishihara, H.; Iwai, K.; Adachi, A.; Takeuchi, S. A dynamic microarray device for paired bead-based analysis. Lab Chip 2010, 10, 2443–2448. [Google Scholar] [CrossRef] [PubMed]
  50. Kumano, I.; Hosoda, K.; Suzuki, H.; Hirata, K.; Yomo, T. Hydrodynamic trapping of Tetrahymena thermophila for the long-term monitoring of cell behaviors. Lab Chip 2012, 12, 3451–3457. [Google Scholar] [CrossRef] [PubMed]
  51. Gervais, T.; El-Ali, J.; Günther, A.; Jensen, K.F. Flow-induced deformation of shallow microfluidic channels. Lab Chip 2006, 6, 500–507. [Google Scholar] [CrossRef] [PubMed]
  52. Smith, A.E.; Zhang, Z.; Thomas, C.R.; Moxham, K.E.; Middelberg, A.P. The mechanical properties of saccharomyces cerevisiae. Proc. Natl. Acad. Sci. USA 2000, 97, 9871–9874. [Google Scholar] [CrossRef] [PubMed]
  53. Bryan, A.K.; Goranov, A.; Amon, A.; Manalis, S.R. Measurement of mass, density, and volume during the cell cycle of yeast. Proc. Natl. Acad. Sci. USA 2010, 107, 999–1004. [Google Scholar] [CrossRef] [PubMed]
  54. Stenson, J.D.; Thomas, C.R.; Hartley, P. Modelling the mechanical properties of yeast cells. Chem. Eng. Sci. 2009, 64, 1892–1903. [Google Scholar] [CrossRef]
  55. Stenson, J.D.; Hartley, P.; Wang, C.; Thomas, C.R. Determining the mechanical properties of yeast cell walls. Biotechnol. Prog. 2011, 27, 505–512. [Google Scholar] [CrossRef] [PubMed]
  56. Burg, T.P.; Godin, M.; Knudsen, S.M.; Shen, W.; Carlson, G.; Foster, J.S.; Babcock, K.; Manalis, S.R. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 2007, 446, 1066–1069. [Google Scholar] [CrossRef] [PubMed]
  57. Lee, J.; Chunara, R.; Shen, W.; Payer, K.; Babcock, K.; Burg, T.P.; Manalis, S.R. Suspended microchannel resonators with piezoresistive sensors. Lab Chip 2011, 11, 645–651. [Google Scholar] [CrossRef] [PubMed]
  58. Khalili, A.A.; Ahmad, M.R. Numerical analysis of hydrodynamic flow in microfluidic biochip for single-cell trapping application. Int. J. Mol. Sci. 2015, 16, 26770–26785. [Google Scholar] [CrossRef] [PubMed]
  59. Khalili, A.A.; Basri, M.A.M.; Ahmad, M.R. Simulation of single cell trapping via hydrodynamic manipulation. J. Teknol. 2014, 69, 121–126. [Google Scholar]

Share and Cite

MDPI and ACS Style

Ahmad Khalili, A.; Ahmad, M.R.; Takeuchi, M.; Nakajima, M.; Hasegawa, Y.; Mohamed Zulkifli, R. A Microfluidic Device for Hydrodynamic Trapping and Manipulation Platform of a Single Biological Cell. Appl. Sci. 2016, 6, 40. https://doi.org/10.3390/app6020040

AMA Style

Ahmad Khalili A, Ahmad MR, Takeuchi M, Nakajima M, Hasegawa Y, Mohamed Zulkifli R. A Microfluidic Device for Hydrodynamic Trapping and Manipulation Platform of a Single Biological Cell. Applied Sciences. 2016; 6(2):40. https://doi.org/10.3390/app6020040

Chicago/Turabian Style

Ahmad Khalili, Amelia, Mohd Ridzuan Ahmad, Masaru Takeuchi, Masahiro Nakajima, Yasuhisa Hasegawa, and Razauden Mohamed Zulkifli. 2016. "A Microfluidic Device for Hydrodynamic Trapping and Manipulation Platform of a Single Biological Cell" Applied Sciences 6, no. 2: 40. https://doi.org/10.3390/app6020040

APA Style

Ahmad Khalili, A., Ahmad, M. R., Takeuchi, M., Nakajima, M., Hasegawa, Y., & Mohamed Zulkifli, R. (2016). A Microfluidic Device for Hydrodynamic Trapping and Manipulation Platform of a Single Biological Cell. Applied Sciences, 6(2), 40. https://doi.org/10.3390/app6020040

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop