Figure 7.
(a) Upper alignment mark; (b) Lower alignment mark.
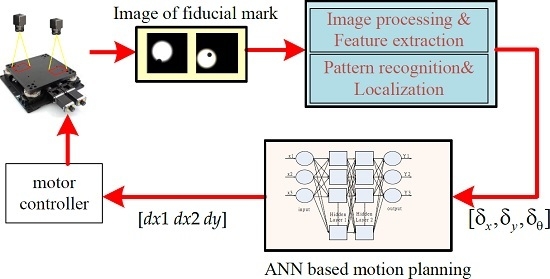
3.1. Image Processing and Pattern Recognition
Before the alignment using the XXY stage is performed, the image processing and recognition are obtained according to the following steps: (1) teaching the pattern of positioning mark; (2) capturing the images by dual GIGA-E CCDs; (3) spatial and frequency filtering; (4) binarization; (5) erosion and dilation; (6) recognizing the positioning mark from the region of interest (ROI) by the pattern matching method, (7) edge detecting the fiducial marks and obtaining the centers of the positioning marks; and (8) transforming the image coordinates to actual Cartesian coordinates. Object detection plays an important role in determining the localization of the alignment mark in this image processing problem. To achieve the image alignment, the most important point is the mark recognition at first. If the mark recognition method is robust and stable, the accuracy of mark recognition can be guaranteed.
Generally, the pattern image should be complete and clear enough for the precision alignment. The pattern of the target image should be obtained by image processing and it is usually called pattern teaching in the AOI software. First, the pattern image is acquired from the ROI as the target image and the captured image is processed by the binarization to become a binary image. After that, the binarized image is processed by morphologically processing to become a cleaner binary image and stored in the PC memory. Second, the binarized image is applied to perform pattern matching to find the located regions of the actual image which are similar to the target pattern image.
Figure 8 is used to describe the relationship between the testing image and the pattern where the gray value of the testing image to be searched at image pixel
(x,
y) is denoted by
f(x,
y) and that of the pattern image is denoted by
w(x,
y). In addition, the size of the testing image is denoted as
M ×
N and the size of the pattern image is
J ×
K. Therefore, the matched score
R(x,
y) between the pattern image and the testing image can be defined as follows.
Based on the above equation, the perfect match is when the value of
R is zero. Otherwise, the larger
R means that the matching case is worse. The above method is called the square difference matching method [
11]. Different from the above method, there is another popular method which uses the normalized correlation coefficient (NCC) between the pattern image and the searched image to determine the matching score; this method is called the NCC matching method [
17]. The definition of the NCC is described as follows.
where
s = 0, 1, 2, …,
M − 1,
t = 0, 1, 2, …,
N − 1,
is the average gray-level value of the pattern,
w(
x,
y), and
is the average gray-level value of the testing image
f(
x,
y). The NCC value has two characteristic properties: (1) the correlation coefficient
r(
s,
t) is normalized in the range between −1 and +1; (2) the larger
r(
s,
t) implies the larger pattern matching. In this study, the NCC method is applied to find the fiducial mark.
Figure 9 illustrates a pattern matching case by the NCC method;
Figure 9a is the actual testing image and
Figure 9b is the pattern image which is binarized.
Figure 9c shows that the captured image is binarized and the pattern matching result using the NCC method is shown in
Figure 9d (the red circle is used to mark the matched image).
Figure 8.
Correlation between w(x, y) and f(x, y).
Figure 8.
Correlation between w(x, y) and f(x, y).
Figure 9.
Pattern recognition steps: (a) Original image; (b) Pattern image; (c) Binarization of original; (d) searched pattern.
Figure 9.
Pattern recognition steps: (a) Original image; (b) Pattern image; (c) Binarization of original; (d) searched pattern.
It is easy for the pattern recognition if there is only one fiducial mark that must be identified. However, to increase the speed of the image-servo mask alignment, the proposed method must capture the upper mark and the lower mark in the one shot. Therefore, some other problems should be solved; for example, the first problem of the halo effect results from the upper and lower masks being located in different depths of field as shown in
Figure 10a. The second problem is that the lower mark may be covered by the upper mark in some cases as shown in
Figure 10b. Therefore, solutions for these two problems are proposed as follows. To achieve the precision alignment task, it is important to determine the position of each fiducial marker with high accuracy. Detection of objects can be performed by using pattern recognition techniques such as neural networks [
18,
19], linear filters [
20], support vector machines [
21], and the Hough Transform [
22]. As the positions of the objects need to be determined with sub-pixel precision, an accurate estimate can be obtained by computing its center of gravity [
17]. However, for the case of
Figure 11b, there are two recognized marks and one of the patterns is an incomplete circle; the COG method could cause a large positioning error for the incomplete circular mark. In that case, the generalized Hough Transform (GHT) is studied to find the dual positioning marks in this paper.
Hough Transform (HT) is proposed by P.V. C. Hough in 1972 and this method can be used to detect the line, circle and arbitrary shape [
22,
23]. To find the circle using circle HT, the first step is to make all edge points connected together to form a closed border; the second step is transferring the coordinates (
x,
y) of all points son the border to the space of parameter (
a,
b,
r); the final step is to obtain the intersection of all cone which is transferred according to all points on the border. For example, consider a circle equation as follows.
where (
a,
b,
r) is the vector of the center of circle with its radius. The circle HT is to represent Equation (7) to the parameter space as follows.
To find the intersection point in this parameter space
H(
x,
y,
a,
b,
r), an accumulator matrix is needed and the parameter space is divided into “buckets” using a grid. Initially, all elements in the matrix are zeros. Then, each edge point in the original space (
x,
y) is substituted into the parameter space to obtain the corresponding parameter (
a,
b,
r). The accumulator matrix is used to count the number of “circles” in that passing through the corresponding grid cell in the parameter space and the number is called “voting number”. After voting, the position of the local maxima in the accumulator matrix represents the circle centers in the original space. To illustrate how to use the circle HT, assume that three points (
x1,
y1), (
x2,
y2), (
x3,
y3) are located at a circle with its radius of
r′. The solution of (
a,
b) for these three points can be described by three cones. Therefore, the intersection of these three cones is the center of the circle (
a′,
b′) as shown in
Figure 11.
Figure 10.
(a) The halo effect of dual marks; (b) the partial lower mark in the upper mark.
Figure 10.
(a) The halo effect of dual marks; (b) the partial lower mark in the upper mark.
Figure 11.
Cones of the three edge points in the parameter space.
Figure 11.
Cones of the three edge points in the parameter space.