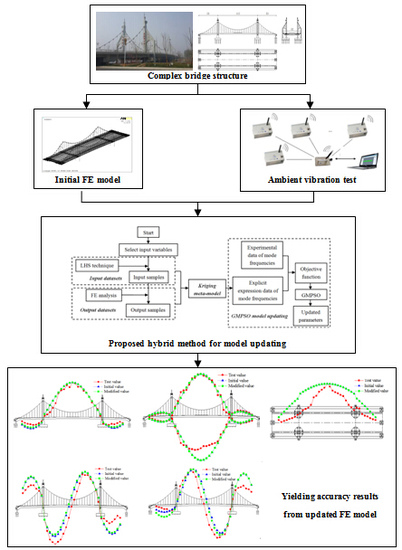
FE Model Updating on an In-Service Self-Anchored Suspension Bridge with Extra-Width Using Hybrid Method
Abstract
:1. Introduction
2. Hybrid Model Updating Method
2.1. GMPSO
- Randomly initializing positions and velocities of N particles and setting the values of serials of parameters such as w, c1, c2, d, Pm, maximum iteration number, and the upper and lower bounds of search space;
- Establishing the objective function, called fitness function and calculating its value of each particle. Recording each particle’s current position and function value in pbest in which the best position and best value are recorded in gbest;
- Renewing velocity of particles based on Equation (1);
- Mutating position of particles at a probability of Pm based on Equation (3);
- Renewing position of particles based on Equation (2);
- Calculating function value again and replacing pbest if the current value is better than the former one.
- Replacing gbest in the current pbest and gbest according to the best value.
- Quitting searching if the iteration number reaches the maximum one or accuracy meets the limitation, otherwise, returning to Step 3.
2.2. Latin Hypercube Sampling with Bounded Parameters
2.3. Kriging Meta-Model
2.4. Hybrid Method
- Applying LHS method to select reasonable samples of random parameters as input datasets;
- Performing a series of the FE analyses with the input parameters to obtain the interested mode frequencies of the structure as the output datasets;
- Determining the architecture of the Kriging meta-model, yielding its correlation coefficients with the input and output datasets with Equations (6)–(10) and extracting the explicit expression based on Equation (11);
- Applying GMPSO as an optimization technique with an objective function which is the sum of natural frequencies residuals between experimental value and Kriging model according to Figure 1;
- Yielding the updated values of parameters after several iterations.
3. Case Study of a Damaged Simply Supported Beam
4. Application to Model Updating of an In-Service Bridge with Extra-Width
4.1. Description of Bridge Structure
4.2. FE Model
4.3. Analysis of Dynamic Characteristics
4.4. Parameters Selected by Sensitivity Analysis
4.5. Model Updating Using Proposed Hybrid Method
5. Conclusions
- Through the application of the hybrid method to a damaged simply supported beam, it was evident that the updating process of hybrid method, compared to direct GMPSO, can be performed more efficiently without losing accuracy. This demonstrates that the proposed hybrid method is applicable to model updating of engineering applications.
- Based on the mode frequency results of ambient vibration test of Hunan Road Bridge, it was clear seen that the differences between the initial FE model and experiment were large enough, some of which are up to 38%, but the vibration modes show high agreements with a lowest MAC value of 0.849. Moreover, due to the extra-width, the torsion mode emerged earlier than ordinary bridges, which enhanced the importance of yielding a precise FE model for further performance evaluation.
- Ten sensitive parameters—module of main girder, main tower and main cable, density of main girder, moment of inertia of vertical bending, transverse bending and torsion, moment of inertia of main tower, area of section of main girder, and secondary dead load—were selected after sensitivity analysis as updated parameters of Hunan Road Bridge. After model updating using hybrid method, both of the mode frequencies and shapes showed a relatively high agreement with the results of the experiment. The differences of mode frequencies drop sharply and are all below 6%. Meanwhile, all the MACs increase over 0.87, which indicates the vibration mode has a higher agreement. The successful model updating of this bridge fills in the blank of model updating of a complex self-anchored suspension bridge. In addition, the updating process makes it possible for other model updating issues of complex bridge structures.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, J.; Li, A.; Feng, M. Sensitivity and reliability analysis of a self-anchored suspension bridge. J. Bridge Eng. 2013, 18, 703–711. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Hu, J.W.; Elbeltagi, E. Evaluation of high-speed railway bridges based on a nondestructive monitoring system. Appl. Sci. 2016, 6, 24. [Google Scholar] [CrossRef]
- Kim, S.H.; Won, J.H. Structural behavior of a long-span partially earth-anchored cable-stayed bridge during installation of a key segment by thermal prestressing. Appl. Sci. 2016, 6, 231. [Google Scholar] [CrossRef]
- Feng, D.; Scarangello, T.; Feng, M.; Ye, Q. Cable tension force estimate using novel noncontact vision-based sensor. Measurement 2017, 99, 44–52. [Google Scholar] [CrossRef]
- Zhao, H.W.; Ding, Y.L.; An, Y.H.; Li, A.Q. Transverse dynamic mechanical behavior of hangers in the rigid tied arch bridge under train loads. J. Perform. Constr. Facil. 2017, 31, 04016072. [Google Scholar] [CrossRef]
- Wang, G.X.; Ding, Y.L.; Song, Y.S.; Wu, L.Y.; Yue, Q.; Mao, G.H. Detection and location of the degraded bearings based on monitoring the longitudinal expansion performance of the main girder of the Dashengguan Yangtze Bridge. J. Perform. Constr. Facil. 2016, 30, 04015074. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, T.; Chai, S. Probabilistic fatigue life prediction of bridge cables based on multiscaling and mesoscopic fracture mechanics. Appl. Sci. 2016, 6, 99. [Google Scholar] [CrossRef]
- Ding, Y.; Li, A. Finite element model updating for the Runyang cable-stayed bridge tower using ambient vibration test results. Adv. Struct. Eng. 2008, 11, 323–335. [Google Scholar] [CrossRef]
- Guo, J.; Zhong, J.; Dang, X.; Yuan, W. Seismic responses of a cable-stayed bridge with consideration of uniform temperature load. Appl. Sci. 2016, 6, 408. [Google Scholar] [CrossRef]
- Cismaşiu, C.; Narciso, A.; Amarante dos Santos, F. Experimental dynamic characterization and finite-element updating of a footbridge structure. J. Perform. Constr. Facil. 2014, 29, 04014116. [Google Scholar] [CrossRef]
- Deng, L.; Cai, C.S. Bridge model updating using response surface method and genetic algorithm. J. Bridge Eng. 2010, 15, 553–564. [Google Scholar] [CrossRef]
- Berman, A.; Flannelly, W.G. Theory of incomplete models of dynamic structure. AIAA J. 1970, 9, 1481–1487. [Google Scholar] [CrossRef]
- Chen, J.C.; Graba, J.A. Analytical model improvement using modal test results. AIAA J. 1980, 18, 684–690. [Google Scholar] [CrossRef]
- Wan, H.; Ren, W. Parameter selection in finite-element-model updating by global sensitivity analysis using Gaussian process metamodel. J. Struct. Eng. 2014, 141, 04014164. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M. Model updating of railway bridge using in situ dynamic displacement measurement under trainloads. J. Bridge Eng. 2015, 20, 04015019. [Google Scholar] [CrossRef]
- Perera, R.; Torres, R. Structural damage detection via model data with genetic algorithms. J. Struct. Eng. 2006, 132, 1491–1501. [Google Scholar] [CrossRef]
- Marwala, T. Finite element model updating using response surface method. In Proceedings of the 45th Collection of Technical Papers-AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Palm Springs, CA, USA, 19–22 April 2004; pp. 5165–5173.
- Gholizadeh, S.; Moghadas, R.K. Performance-based optimum design of steel frames by an improved quantum particle swarm optimization. Adv. Struct. Eng. 2014, 17, 143–156. [Google Scholar] [CrossRef]
- Xiang, J.; Zhong, Y. A novel personalized diagnosis methodology using numerical simulation and an intelligent method to detect faults in a shaft. Appl. Sci. 2016, 6, 414. [Google Scholar] [CrossRef]
- Si, L.; Wang, Z.; Liu, Z.; Liu, X.; Tan, C.; Xu, R. Health condition evaluation for a shearer through the integration of a fuzzy neural network and improved particle swarm optimization algorithm. Appl. Sci. 2016, 6, 171. [Google Scholar] [CrossRef]
- Nanda, B.; Maity, D.; Maiti, D.K. Crack assessment in frame structures using modal data and unified particle swarm optimization technique. Adv. Struct. Eng. 2014, 17, 747–766. [Google Scholar] [CrossRef]
- Kaveh, A.; Nasrolahi, A. A new probabilistic particle swarm optimization algorithm for size optimization of spatial truss structures. Int. J. Civ. Eng. 2014, 12, 1–13. [Google Scholar]
- Do, D.M.; Gao, W.; Song, C.; Tangaramvong, S. Dynamic analysis and reliability assessment of structures with uncertain-but-bounded parameters under stochastic process excitations. Reliab. Eng. Syst. Saf. 2014, 132, 46–59. [Google Scholar] [CrossRef]
- Liao, Z.X.; Zhong, W.M.; Qian, F. Particle swarm optimization algorithm based on mutation of Gaussian white noise disturbance. J. East China Univ. Sci. Tech. (Nat. Sci. Ed.) 2008, 34, 859–863. (In Chinese) [Google Scholar]
- Ren, W.X.; Fang, S.E.; Deng, M.Y. Response surface-based finite-element-model updating using structural static responses. J. Eng. Mech. 2011, 137, 248–257. [Google Scholar] [CrossRef]
- Simon, P.; Goldack, A.; Narasimhan, S. Mode shape expansion for lively pedestrian bridges through Kriging. J. Bridge Eng. 2016, 21, 04016015. [Google Scholar] [CrossRef]
- Dette, H.; Pepelyshev, A. Generalized Latin hypercube design for computer experiments. Technometrics 2010, 52, 421–429. [Google Scholar] [CrossRef]









| Parameter | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Experimental model | 1.000 | 1.000 | 0.700 | 1.000 | 1.000 | 1.000 | 1.000 | 0.700 | 1.000 | 1.000 |
| Direct GMPSO | 0.991 | 0.945 | 0.717 | 0.978 | 1.005 | 1.037 | 0.982 | 0.729 | 0.980 | 1.034 |
| Hybrid method | 1.025 | 1.016 | 0.735 | 0.932 | 0.932 | 1.078 | 1.008 | 0.668 | 0.968 | 0.993 |
| Mode | Experimental Frequency/Hz | Updated Frequency/Hz | Difference/% | ||
|---|---|---|---|---|---|
| Direct GMPSO | Hybrid Method | Direct GMPSO | Hybrid Method | ||
| 1 | 15.39069 | 15.43708 | 15.31826 | 0.30 | 0.47 |
| 2 | 37.14974 | 37.25102 | 37.14082 | 0.27 | 0.02 |
| 3 | 52.36193 | 52.31448 | 52.41372 | 0.09 | 0.10 |
| 4 | 83.96296 | 83.96269 | 83.58468 | 0.00 | 0.45 |
| 5 | 96.36669 | 96.79726 | 96.11117 | 0.45 | 0.27 |
| 6 | 116.64350 | 116.43540 | 116.98770 | 0.18 | 0.30 |
| 7 | 144.77070 | 145.07480 | 144.88010 | 0.21 | 0.08 |
| 8 | 184.79670 | 186.12250 | 184.99380 | 0.72 | 0.11 |
| 9 | 223.79820 | 223.20420 | 223.93680 | 0.27 | 0.06 |
| 10 | 254.07320 | 255.31840 | 254.94600 | 0.49 | 0.34 |
| Mode | Theoretical Frequency/Hz | Modal Shape | Experimental Frequency/Hz | Difference/% | MAC 2 |
|---|---|---|---|---|---|
| 1 | 0.7208 | First order of vertical bending | 0.9030 | 25.28 | 0.979 |
| 2 | 1.0643 | First order of torsion | 1.3670 | 28.44 | 0.973 |
| 3 | 1.3378 | First order of transverse bending | 1.3790 | 3.08 | 0.915 |
| 4 | 1.3892 | Second order of vertical bending | 1.9290 | 38.60 | 0.894 |
| 5 | 1.7504 | Third order of vertical bending | 2.4170 | 38.08 | 0.849 |
| Mode | Experimental Frequency/Hz | Updated Frequency/Hz | Difference/% |
|---|---|---|---|
| 1 | 0.9030 | 0.9161 | 1.45 |
| 2 | 1.3670 | 1.3427 | 1.78 |
| 3 | 1.3790 | 1.4600 | 5.87 |
| 4 | 1.9290 | 1.8246 | 5.41 |
| 5 | 2.4170 | 2.2810 | 5.63 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, Z.; Li, A.; Li, J.; Duan, M. FE Model Updating on an In-Service Self-Anchored Suspension Bridge with Extra-Width Using Hybrid Method. Appl. Sci. 2017, 7, 191. https://doi.org/10.3390/app7020191
Xia Z, Li A, Li J, Duan M. FE Model Updating on an In-Service Self-Anchored Suspension Bridge with Extra-Width Using Hybrid Method. Applied Sciences. 2017; 7(2):191. https://doi.org/10.3390/app7020191
Chicago/Turabian StyleXia, Zhiyuan, Aiqun Li, Jianhui Li, and Maojun Duan. 2017. "FE Model Updating on an In-Service Self-Anchored Suspension Bridge with Extra-Width Using Hybrid Method" Applied Sciences 7, no. 2: 191. https://doi.org/10.3390/app7020191
APA StyleXia, Z., Li, A., Li, J., & Duan, M. (2017). FE Model Updating on an In-Service Self-Anchored Suspension Bridge with Extra-Width Using Hybrid Method. Applied Sciences, 7(2), 191. https://doi.org/10.3390/app7020191