Numerical Analysis and Optimization on Piezoelectric Properties of 0–3 Type Piezoelectric Cement-Based Materials with Interdigitated Electrodes
Abstract
:1. Introduction
2. Methodology
2.1. Establishment of Characteristic Matrix of IEPCM
2.2. Piezoelectric Constitutive Equation of IEPCM
2.3. Modeling of IEPCM
- (1)
- Establishment of material model—the same solid 226-type element is employed to establish two material models. The matrix coefficients shown in Table 1, Table 2 and Table 3 are fed into ANSYS software in sequence, and to establish the material model 1 with the polarized direction pointing to the positive part of the x-axis. The material model 2 can be constructed by feeding with opposite values in Table 2 and the same values in Table 1 and Table 3.
- (2)
- Establishment of geometric model—a small rectangle with length (L) of 0.00025 m, width (B) of 0.01 m and H of 0.001 m is established. Two hundred rectangles are copied along the positive direction of x-axis, an integrity rectangle are grown up with L of 0.05 m. Moreover, the W, P of this IEPCM is designed as 0.00025 m, 0.0001 m, respectively.
- (3)
- Grid meshing—the material model 1 and model 2 is selected and defined, the unit size is divided, and grid meshed, respectively.
- (4)
- Voltage load applying—voltage load (0 V, 10 V) is applied onto the negative, positive electrodes, in turn. For simplification, the main supporting parts of positive and negative electrodes are neglected in this simulation.
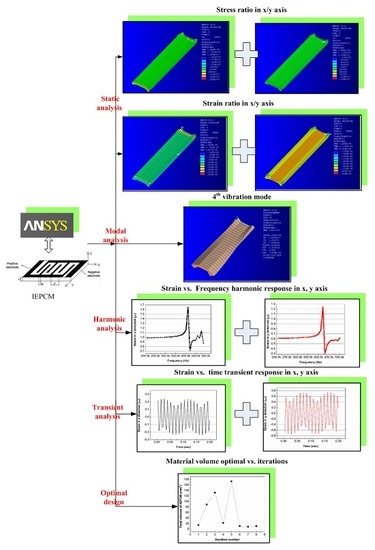
3. Static/Dynamic Response Characteristics of IEPCM
3.1. Static Response Analysis of IEPCM
3.2. Modal Analysis of IEPCM
3.3. Harmonic Response Analysis of IEPCM
3.4. Transient Response Analysis of IEPCM
4. Optimal Design of IEPCM
5. Conclusions
- (1)
- The maximum strain ratio at both ends of IEPCM in the x- and y-direction is 3.19, whereas that in the middle region is 2.69. These values indicate that good orthotropic characteristics and lateral piezoelectric driving capacity can be produced for 0–3 type IEPCMs.
- (2)
- The modal frequency distribution of the IEPCM is crowded together but with no repeated frequency; the vibration mode of the IEPCM is orthogonal, whereas the resonance frequency is 210.3 kHz. The harmonic responses of the IEPCM either in the x- and y-direction are almost the same at 420 kHz, which indicates some hysteresis characteristics exist. The load region of the driving voltage has a significant influence on the transient dynamic property of the IEPCM.
- (3)
- When the wafer width Wp of 0–3 type IEPCM is set at 1 mm, the main physical parameters of the optimal design for the IEPCM are achieved as follows: the thickness H is 0.62 mm, the electrode width W is 0.73 mm, the electrode spacing P is 1.02 mm and the corresponding volume VTOT is 10.9 mm3.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PCM | Piezoelectric cement-based material |
| IEPCM | Piezoelectric cement-based material with interdigitated electrodes |
| SHM | Structural health monitoring |
| PZT | Lead-zirconate-titanate |
References
- Han, B.; Wang, Y.; Dong, S.; Zhang, L.; Ding, S.; Yu, X.; Ou, J. Smart concrete and structures: A review. J. Intell. Mater. Syst. Struct. 2015, 26, 1303–1345. [Google Scholar] [CrossRef]
- Wen, S.; Chung, D.D.L. Model of piezoresitivity in carbon fiber cement. Cem. Concr. Res. 2006, 36, 1879–1885. [Google Scholar] [CrossRef]
- Han, B.; Yu, X.; Ou, J. Self-Sensing Concrete in Smart Structures; Butterworth-Heinemann, Elsevier Science: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Li, G.Y.; Wang, P.M.; Zhao, X.H. Pressure-sensitive properties and microstructure of carbon nanotube reinforced cement composites. Cem. Concr. Compos. 2007, 29, 377–382. [Google Scholar] [CrossRef]
- Azhari, F.; Banthia, N. Cement-based sensors with carbon fibers and carbon nanotubes for peizoresistive sensing. Cem. Concr. Compos. 2012, 34, 866–873. [Google Scholar] [CrossRef]
- Konsta-Gdoutos, M.S.; Aza, C.A. Self-sensing carbon nanotube (CNT) and nanofiber (CNF) cementitious composites for real time damage assessment in smart structures. Cem. Concr. Compos. 2014, 53, 110–128. [Google Scholar] [CrossRef]
- Galao, O.; Baeza, F.J.; Zornoza, E.; Garces, P. Strain and damage sensing properties on multifunctional cement composites with CNF admixture. Cem. Concr. Compos. 2014, 46, 90–98. [Google Scholar] [CrossRef] [Green Version]
- D’Alessandro, A.; Ubertini, F.; Materazzi, A.L.; Porfiri, M.; Laflamme, S. Electromechanical modelling of new nanocomposite carbon cement-based sensors for structural health monitoring. Struct. Health Monit. 2015, 14, 137–147. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Rallini, M.; Ubertini, F.; Materazzi, A.L.; Kenny, J.M. Investigations on scalable fabrication procedures for self-sensing carbon nanotube cement-matrix composites for SHM applications. Cem. Concr. Compos. 2016, 65, 200–213. [Google Scholar]
- Luo, J.L.; Chung, K.L.; Li, Q.Y.; Chen, S.J.; Li, L.; Hou, D.S.; Zhang, C.W. Piezoresistive properties of cement composites reinforced by functionalized carbon nanotubes using photo-assisted Fenton. Smart Mater. Struct. 2017, 26, 035025. [Google Scholar] [CrossRef]
- Li, Z.J.; Zhang, D.; Wu, K.R. Cement-based 0–3 piezoelectric composites. J. Am. Ceram. Soc. 2002, 85, 305–313. [Google Scholar] [CrossRef]
- Huang, S.F.; Chang, J.; Lu, L.C.; Chen, X. Preparation and polarization of 0–3 cement-based piezoelectric composites. Mater. Res. Bull. 2006, 41, 291–297. [Google Scholar] [CrossRef]
- Chaipanich, A.; Rianyoi, R.; Potong, R.; Jaitanong, N. Aging of 0–3 piezoelectric PZT ceramic–Portland cement composites. J. Ceram. Int. 2014, 40, 13579–13584. [Google Scholar] [CrossRef]
- Luo, J.L.; Zhang, S.; Wei, X.; Li, Q.Y.; Li, L.; Sun, S.W. Preparation and piezoelectric properties of CNT modified cement-based piezoelectric composites. Piezoelectr. Acoustoopt. 2015, 37, 437–440. (In Chinese) [Google Scholar]
- Li, Z.J.; Gong, H.Y.; Zhang, Y.J. Fabrication and piezoelectricity of 0–3 cement based composite with nano-PZT powder. Curr. Appl. Phys. 2009, 9, 588–591. [Google Scholar] [CrossRef]
- Gong, H.Y.; Zhang, H.Y.; Che, S.W. Influence of carbon black on properties of PZT-cement piezoelectric composites. J. Compos. Mater. 2010, 44, 2547–2557. [Google Scholar]
- Lan, K.H.; Chan, H.L.W. Piezoelectric cement-based 1–3 composites. Appl. Phys. A 2005, 81, 1451–1454. [Google Scholar]
- Quant, M.; Elizalde, H.; Flores, A.; Ramirez, R.; Orta, P.; Song, G.B. A comprehensive model for piezoceramic actuators: Modeling, validation and application. Smart Mater. Struct. 2009, 18, 125011. [Google Scholar] [CrossRef]
- Xu, Y.L.; Qian, Y.; Chen, J.J.; Song, G.B. Modal-based mixed vibration control for uncertain piezoelectric flexible structures. Struct. Eng. Mech. 2015, 55, 229–244. [Google Scholar] [CrossRef]
- Hong, X.; Wang, H.; Wang, T.; Liu, G.; Li, Y.; Song, G.B. Dynamic cooperative identification based on synergetic for pipe structural health monitoring with piezoceramic transducers. Smart Mater. Struct. 2013, 22, 045003. [Google Scholar] [CrossRef]
- Jaitanong, N.; Yimnirun, R.; Zeng, H.R.; Li, G.R.; Yin, Q.R.; Chaipanich, A. Piezoelectric properties of cement based/PVDF/PZT composites. Mater. Lett. 2014, 130, 146–149. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Peng, Y.P.; Xu, D.Y.; Cheng, X. FEM analysis of 1–3 cement based piezoelectric composites. Adv. Mater. Res. 2010, 123–125, 539–542. [Google Scholar] [CrossRef]
- Wickramasinghe, V.K.; Hagood, N.W. Durability characterization of active fiber composite actuators for helicopter rotor blade applications. In Proceedings of the 44th AIAA/ASME/ASCE/AHS Conference, Norfolk, Virginia, 7–10 April 2003; pp. 7–10.
- Hagood, N.W.; Kindel, R.; Ghandi, K. Improving transverse actuation of piezoceramics using interdigitated surface electrodes. SPIE 1993, 1917, 341–352. [Google Scholar]
- Roundy, S. On the effectiveness of vibration-based energy harvesting. J. Intell. Mater. Syst. Struct. 2005, 16, 809–823. [Google Scholar] [CrossRef]
- Lin, X.J.; Huang, S.F.; Zhou, K.C.; Zhang, D. The influence of structural parameters on the actuation performance of piezoelectric fiber composites. Mater. Des. 2016, 107, 123–129. [Google Scholar] [CrossRef]
- Liu, Z.H.; Pan, C.T.; Su, C.Y.; Lin, L.W.; Chen, Y.J.; Tsai, J.S. A flexible sensing device based on a PVDF/MWCNT composite nanofiber array with an interdigital electrode. Sens. Actuators A 2014, 211, 78–88. [Google Scholar] [CrossRef]
- Chidambaram, N.; Balma, D.; Nigon, R.; Mazzalai, A.; Matloub, R.; Sandu, C.S.; Muralt, P. Converse mode piezoelectric coefficient for lead zirconatetitanate thinfilm with interdigitated electrode. J. Micromech. Microeng. 2015, 25, 045016. [Google Scholar] [CrossRef]







| Item | Value | Item | Value | Item | Value | Item | Value | Item | Value | Item | Value |
|---|---|---|---|---|---|---|---|---|---|---|---|
| C11 | 103.7 | ||||||||||
| C12 | 67.0 | C22 | 119.1 | (Symmetry) | |||||||
| C13 | 67.0 | C23 | 70.2 | C33 | 119.1 | ||||||
| C14 | 0 | C24 | 0 | C34 | 0 | C44 | 23.5 | ||||
| C15 | 0 | C25 | 0 | C35 | 0 | C45 | 0 | C55 | 28.0 | ||
| C16 | 0 | C26 | 0 | C36 | 0 | C46 | 0 | C56 | 0 | C66 | 23.5 |
| ε11 | ε22 | ε33 |
|---|---|---|
| 4.22 | 4.85 | 4.85 |
| Stress Direction | X Axis | Y Axis | Z Axis | |
|---|---|---|---|---|
| E-Field Direction | ||||
| X | e11 (15.1) | e12 (0) | e13 (0) | |
| Y | e21 (−5.2) | e22 (0) | e23 (0) | |
| Z | e31 (−5.2) | e32 (0) | e33 (0) | |
| XY | e41 (0) | e42 (12.7) | e43 (0) | |
| YZ | e51 (0) | e52 (0) | e53 (0) | |
| XZ | e61 (0) | e62 (0) | e63 (12.7) | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; You, C.; Zhang, S.; Chung, K.L.; Li, Q.; Hou, D.; Zhang, C. Numerical Analysis and Optimization on Piezoelectric Properties of 0–3 Type Piezoelectric Cement-Based Materials with Interdigitated Electrodes. Appl. Sci. 2017, 7, 233. https://doi.org/10.3390/app7030233
Luo J, You C, Zhang S, Chung KL, Li Q, Hou D, Zhang C. Numerical Analysis and Optimization on Piezoelectric Properties of 0–3 Type Piezoelectric Cement-Based Materials with Interdigitated Electrodes. Applied Sciences. 2017; 7(3):233. https://doi.org/10.3390/app7030233
Chicago/Turabian StyleLuo, Jianlin, Chenglin You, Shuai Zhang, Kwok L. Chung, Qiuyi Li, Dongshuai Hou, and Chunwei Zhang. 2017. "Numerical Analysis and Optimization on Piezoelectric Properties of 0–3 Type Piezoelectric Cement-Based Materials with Interdigitated Electrodes" Applied Sciences 7, no. 3: 233. https://doi.org/10.3390/app7030233
APA StyleLuo, J., You, C., Zhang, S., Chung, K. L., Li, Q., Hou, D., & Zhang, C. (2017). Numerical Analysis and Optimization on Piezoelectric Properties of 0–3 Type Piezoelectric Cement-Based Materials with Interdigitated Electrodes. Applied Sciences, 7(3), 233. https://doi.org/10.3390/app7030233