1. Introduction
The magnitude of initial returns in initial public offerings (IPOs) has been puzzling both researchers and practitioners for decades. The difference between the offering price and the first closing price regularly results in sizeable gains or losses. Among these, there is a bias in the distribution of initial returns that is positive and heavily skewed to the right. For this reason, first-day initial returns are often referred to in the literature as IPO underpricing.
During the Internet bubble of the late 1990s, when the market was very hot, a substantial portion of the companies taken public in the USA more than doubled their offering price in the first day and the phenomenon often resulted in headlines in the news. Ritter and Welch [
1] researched the phenomenon, and reported that the average initial return on a sample of 6249 companies taken public in the USA between 1980 and 2001 was 18.8%. More recently, the number of IPOs has dramatically gone down, and so has the average initial return. Having said that, in 2014 Castlight, San Francisco, CA, USA, a health care software company, soared 149% during its first trading day. Another recent example, though more limited, would be Alibaba Group, Hangzhou, China, the e-commerce giant. This corporation showed a 38% increase from its initial public offering price on the day it went public.
The academic literature has been tracking first-day trading returns in initial public offerings (IPOs) for a long time. Over time, researchers have postulated a large number of explanatory theories, and it is still a very active field of investigation. The vast majority of the empirical analyses carried out to explain and predict underpricing relying on variables related to the structure of the offerings are based on linear models. There have been, however, a number of efforts trying to predict first-day returns using computational intelligence.
Among the latter, we should mention the work of Jain and Nag [
2]. These authors try to predict the post-issue market price using artificial neural networks. More recently, Reber et al. [
3], Meng [
4], Chen [
5], and Esfahanipour et al. [
6] followed suit with the same technique. This line was complemented by Quintana et al. [
7] and Luque et al. [
8], who explored the problem using evolutionary algorithms. Others, such as Chou et al. [
9], used a combination of both of them.
In this paper, we suggest that there is an instrument that has not been tested in the domain yet, that has the potential to be extremely valuable. In a field where the presence of outliers and the problem of overfitting severely affects the performance of predictive algorithms, random forests [
9], are likely to bring a great deal to the table. For this reason, we intend to benchmark the random forests on a sample from the USA financial markets against a number of classic machine learning alternatives that represent different algorithm categories.
The rest of the paper will be structured as follows: in
Section 2, we provide a brief introduction to random forests and introduce both the explanatory variables and the sample that will be used in the analysis;
Section 3 will be used to report the experimental results; that will be followed by a discussion in
Section 4; and, finally,
Section 5 will cover the summary and conclusions.
2. Materials and Methods
Random forests [
10] are ensemble learning methods that combine trees of predictors. This approach, which is usually treated as a supervised method, creates sets of decision trees that vote for the most popular class for vectors according to a number of features.
The trees in a forest are created according to a procedure that is similar to classification and regression trees. The previous element is combined with randomized node optimization and bagging. According to Breiman, the author who introduced the technique, the process follows three key ideas:
Each tree is grown based on a unique training set that is generated by a random sampling with replacement from the original dataset. The size of this new sample mirrors the size of the initial one.
For every node, a subset of the original input variables is selected at random, and the best-performing split on these is used to split the node. The size of the mentioned subset is kept constant during the forest growing.
Trees are grown to the largest extent possible while complying with a minimum number of training patterns at a terminal node constraint, leaf size, and there is no pruning.
The resulting set can then be used to make predictions using a voting mechanism. The process simply entails obtaining individual class predictions for unseen samples from all the components of the forest, and assigning the data pattern to the majority vote.
This technique is applicable to both classification and regression tasks. IPO underpricing prediction falls in the latter category. In this case, tree predictors take on numerical values instead of class labels, and the predictor is formed by taking the average prediction from the tree set.
Random forests show a major strength vs. other tree-based techniques, such as bagging, that is likely to be useful in the IPO domain. Specifically, the ability to combine strong and weak variables to generate models where the former do not dominate tree generation is a key property. The reason is that it affects the correlation among tree output and, therefore, the generalization error of the model. Krauss et al. [
11] show that random forests are the dominant single method for deriving trading decisions on the Standard and Poor′s (S&P) 500 stock universe vis-à-vis deep neural networks and gradient-boosted trees. Other general properties that are relevant in the IPO underpricing prediction domain are its relative robustness with regard to outliers in training data and the fact that it does not overfit.
The use of random forests to tackle financial problems is not new. Recent papers illustrate potential application areas, such as trading [
12], bankruptcy prediction [
13,
14], or credit rating prediction [
15], but, as we mentioned in the introduction, despite the desirable traits, its suitability for IPO underpricing prediction is still to be studied.
2.1. Variables
The starting point to study the phenomenon of IPO underpricing, the most prevalent target variable on IPO research, is providing a formal definition. IPO underpricing,
Ri, is defined in this paper as the percentage difference between the offer price and the closing price on the first trading day, adjusted for the market return:
where
Poi represents the offering price for stock
i;
Pci is the closing price for stock
i;
Moi is the opening for the broad market index of the market where stock
i was taken public for the day before the IPO and
Mci is the closing for market index on the day of the IPO. For the purposes of this study, the relevant indices are the S&P 500, AMEX Composite Index, and NASDAQ Composite Index.
As we have already discussed, the body of research on IPO initial returns is vast. The number of explanations and variables that have been postulated to explain the phenomenon is very wide. However, there is a set of independent variables concerning the structure of the offerings that show up in the literature very often. Among them, we relied on six that we will succinctly describe: width of the price range; offer price; price adjustment; relation to the tech sector; offering size; and retained stock.
Width of price range (RANGE): the width of the non-binding reference price range offered to potential investors during the roadshow has been traditionally considered to have a signaling effect. Wider ranges show uncertainty regarding the valuation of the company and, therefore, tend to be associated with riskier investments. Following [
16,
17], this indicator will be defined as the difference between the maximum and minimum price, divided by the minimum.
Offering price (PRICE): the final offering price is considered a key value, not only as a component of previous indicators, but in its own right. Studies such as [
18,
19], among others, support the idea that price itself might be identified by potential buyers as a quality indicator.
Price adjustment (P_ADJ): many studies such as Hanley [
16], Benveniste and Spindt [
20], or Ljungqvist and Wilhelm [
21] show that relation between the initial tentative price range and the final offer price might be interpreted as a signal by investors. These authors suggest that this effect is likely to be captured the expression that follows:
where
Pf is the offer price and
Pe, the expected price, is the price at the middle of the non-binding reference range.
Technology (TECH): companies whose industrial activities are related to the technology sector tend to show higher initial returns. This is usually controlled in the models by means of a dummy variable that equals one for tech companies and zero otherwise [
22,
23,
24]. Our labeling criterion will be based on the definition used by IPO Monitor. This company classifies IPOs according the US Standard Industry Codes and activities reported by the companies in their filings. Hence, we will consider IPOs to be “tech-related” if IPO Monitor considers them so in their reports.
Offering size (LSIZE): studies such as [
19,
25,
26] defend the importance of including this factor in the models. The variable is defined as the logarithm of the size of the offering, in millions of dollars, excluding the over-allotment option.
Retained stock (RETAINED): the amount of capital retained by initial investors has been traditionally interpreted as a signal of the quality of the stock, as it would reveal the confidence of insiders in the future of the company [
21,
27]. Since we lack the breakdown of primary and secondary shares, this variable will be proxied by the ratio of the amount of shares sold at the IPO divided by the post-offering number of shares minus the shares sold at the IPO.
2.2. Data
The experimental work is based on a sample of 866 companies taken public between January 1999 and May 2010 in three US stock markets, AMEX, NASDAQ, and NYSE (the New York Stock Exchange). As it is customary in IPO research, it excludes closed-end funds; American Depositary Receipts; Real estate investment trusts (REITs), and unit offerings. The primary source of data was the commercial provider IPO Monitor. Missing information was completed with data from a second data vendor, Hoovers. Finally, index information was retrieved from DataStream (S&P 500) and NASD (NASDAQ and AMEX composites).
Table 1 reports the main descriptive statistics (mean, median, standard deviation, minimum, and maximum) for the sample.
Figure 1 shows the return distribution. As we can see, it shows a positive mean return, high kurtosis, and the classic right-skewness corresponding to several hot IPOs with extremely high initial returns (in this case, the most extreme case almost got to quadruple the offering price with a 372% price increase). The mentioned basic characteristics are consistent with the structure of the sample used in previous studies, such as [
1,
7,
18,
19,
21], among many others.
2.3. Methodology
The experimental analysis started with an initial exploratory analysis followed by the main experiments intended to test the predictive accuracy of random forests.
As a first step, we selected the appropriate parameters for the algorithm: leaf size and number of grown trees. This initial analysis was made on a subset of 256 patterns, approximately 30% of the data. The selection of the set of IPOs included in this subsample was random, and these patterns were excluded from the test sample used in the main experiments, that comprised of the remaining 610 IPOs.
We chose one third of the input features for decision splits at random and subsequently tested different combinations of number of trees and leaf sizes ranging from five to 25. As we can see in
Figure 2, these parameters have a major impact on the results.
We conducted several experiments and we saw that the progressive addition of trees resulted in patterns of out-of-bag, OOB, prediction errors such as the one represented in the figure. There, we can observe that the root mean square error (RMSE) on the cases left out of the bootstrap sample used in the construction of the trees tends to stabilize with 40–50 elements. For this reason, we decided to set the number of grown trees at 45. We also fixed at five the minimum number of training patterns per terminal node. It is worth noting that this figure matches the standard rule-of-thumb used in regression problems.
As part of this preliminary analysis, we also studied the relative explanatory power of the independent variables. We assessed the out-of-bag feature importance by the mean decrease in accuracy [
28]. This indicator, also known as permutation importance, evaluates the contribution of independent variables by removing the association between predictor variables and the target. The rationale is that a random permutation of the values of the feature mimics the absence of the variable from the model, and the resulting increase of error can be used as an importance measure. More formally, the procedure carried out was the following: for any variable, we computed the increase in the prediction error if the values of that variable were permuted across the out-of-bag observations. Once we obtained the measure for every tree, we averaged it over the entire ensemble and divided it by the standard deviation for the entire ensemble. The last step was carried out to standardize the raw variable importance score. The results of this process are reported in
Figure 3. There, we can see how the offering price is the most relevant variable in the set. The second, most explanatory variable is the price adjustment made by the seller once he has received the initial show of interest during the road-show, closely followed by the offering size. Among the rest, the dummy variable signaling whether the company is part of the tech sector or not, seems to be the least important one. The prevalence of price vs. the rest clearly illustrates the need for a technique that efficiently combines strong and weak variables that we mentioned in the introduction to random forests.
2.4. Benchmarks
We intend to benchmark random forests against a set of machine learning alternatives. For implementation purposes, we will rely on a very popular collection of machine learning algorithms called WEKA (Waikato Environment for Knowledge Analysis) [
29]. The algorithms we will use as benchmarks are: instance-based learning algorithms (IBK); least median of squares regression (LMSReg); locally-weighted learning (LWL); M5 model trees (M5P); M5 model rules (M5Rules); multilayer perceptron (MLP); radial basis function networks (RBFN); and support vector machines trained with sequential minimal optimization (SMO-Reg). This selection of algorithms includes different categories, such as alternatives based on functions, nearest neighbors, rules, and decision trees.
IBK [
30]: an implementation of a
K-nearest neighbor classifier.
LMSReg [
31]: a robust linear regression approach that filters out outliers in order to enhance accuracy.
LWL [
32]: a local instance-based learning algorithm that builds classifiers based on weighted instances.
M5P [
33]: a numerical classifier that combines standard decision trees with linear regressions to predict continuous variables.
M5Rules [
34]: the algorithm generates decision lists for regression problems using divide-and-conquer. It builds regression trees using M5 in every iteration, and then it turns the best leaves into rules.
MLP [
35]: a standard feed-forward artificial neural network that simulates the biological process of learning through weight adjusting. The algorithm used to train the networks will be back-propagation.
RBFN [
36]: a type of artificial neural network that uses a combination radial basis functions to approximate the structure of the input space.
SMO-Reg [
37]: a support vector machine trained with the sequential minimal optimization algorithm.
All these are described in more detail in
Appendix A.
Table 2 summarizes the parameters used to run these algorithms. The selection of the specific values was made according to the performance of the algorithms in an exploratory analysis. Different configurations were tested on the same portion of the sample used to parameterize the random forests, and the final choice was made according to predictive accuracy in terms of RMSE using a 10-fold cross validation. A summary of configurations and results is reported in
Appendix B. The results for stochastic algorithms average the outcome of three different experiments.
The models will be assessed by their predictive accuracy in terms of RMSE on the same dataset. In order to make the results as general as possible, we will perform a 10-fold cross-validation. Given the stochastic nature of most of the algorithms, including random forests, we will run the experiments 15 times using different random seeds and compare the average results. We will, however, report the main descriptive statistics of these averages to ensure that the image is complete.
3. Results
In this section we report the results of the experimental analysis performed to test the suitability of the random forest algorithm for the IPO underpricing prediction domain.
The main experimental results are reported in
Table 3. There, we provide the main descriptive statistics for the RMSE obtained in the 15 repetitions of the 10-fold cross-validation. For stochastic algorithms we report the average, median, variance, maximum, and minimum. The exception to this is SMO-Reg. Even though it has a stochastic component and we used different seeds, the 15 experiments converged to the exact same solution.
The statistical significance of the differences reported in
Table 3 was tested formally. Given the distribution of the prediction errors, we relied on the Mann–Whitney test [
38]. The results of this analysis are reported in
Table 4. There, we represent the fact that the algorithm in the row has median prediction error that is significantly larger than the one in the column at 1% by “++”. In case a similar difference in the opposite direction is found, the symbol used is “--”. If the disparity is such that the first one is significantly smaller at 5%, we use “-”. Finally, if the possibility of equal predictive accuracy cannot be discarded at 5%, we report “=”.
Following [
3], we complement the analysis based on predictive performance illustrating the potential economic benefits of using these techniques to price IPOs. In
Table 5 we compare the actual observed underpricing with the initial returns resulting should we use forecasts of the models as the offering price. For each of the models, we provide the average value of the statistics on the 610-pattern test set over 15 experiments. That is, we report the average mean underpricing, average median underpricing, and the average of the standard deviations. All of the differences between the median mean observed underpricing and model-based ones were significant at 1%.
Random forests can also be used in this context as an investment tool. A potential trading strategy would be investing in IPOs with the highest initial return potential according to the models. Even though the predictions for initial returns might not be completely accurate, the distribution of forecasts could provide very valuable insights. This is evidenced by
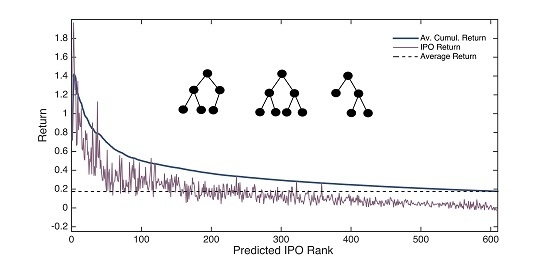
Figure 4. There, we report the returns obtained investing in IPOs prioritized according to the forecasts of the models. The 610 IPOs that compose the test set were ranked by predicted return. Given that we repeated the experiments 15 times, we obtained as many ranks. The IPO Return series shows the average of the actual returns that correspond to the 15 IPOs that have the same rank. The series labeled Av. Cumul. Return, represents the cumulative average of actual returns. For example, the return for IPO 100 was obtained by computing the actual mean underpricing of the 100 companies with the highest predicted initial return. This process was repeated for the 15 experiments, and we report the observed mean cumulative average return. Finally, we include the actual average underpricing to represent the naïve strategy of investing in all IPOs.
4. Discussion
As we can in
Table 3, random forests provide the best results, followed by IBK. In addition to the relatively low mean and median RMSE, we should highlight the fact that the approach seems to be the second-most reliable one among those with a stochastic component. The range of variation for the prediction error is narrow and its variance is relatively low. It was only beaten by SMO-Reg. This algorithm offered an intermediate performance in terms forecasting ability, but converged to the same solution across the 15 experiments.
On the opposite side of the spectrum, LWL and MLP offered the worst results. Even though multi-layer perceptrons have been successfully used in many regression tasks, their sensitivity to the presence of outliers drags its performance in this domain. Conversely, random forests handle this difficulty with much more efficacy. MLP showed the highest dispersion of results, including the worst prediction error in one of the executions.
If we consider the potential economic implications of the potential of using random forests in this domain, the results lay down two interesting applications: IPO pricing, and investing. On the first front, random forests offered the lowest average difference between the actual closing price and the predicted one. This reduced model-based underpricing, where offer price is replaced with the output of the model, came together with the smallest average standard deviation. The implication is that the use of this algorithm to support the pricing decision is likely to have the potential to reduce the amount of money left of the table.
On the second front,
Figure 4 makes it apparent that there could be room for profitable trading based on the output of the models. Even though we cannot claim that random forests make perfect initial return predictions based on the variables discussed, they show good capabilities ranking them. IPOs that are predicted to offer the highest initial returns suffer significantly higher underpricing than the expected bottom performers.
As we can see by the spikes of the IPO Return series, the models do not have the ability to rank perfectly. The highest initial return does not correspond to the first element of the series, and it is far from smooth. In addition to that, the 15 experiments do not result in the same rank (that is, the reason why the maximum value of the series is lower than the highest initial return). Having said that, as the highest values clearly tend to be at the beginning of the series and the lowest at the end, if we invested if the n most promising ones we would be very likely to gain excess returns. That would happen as long as the average return, shown in the Average Cumulative Return series, is higher than the IPO market return, Average Return, and the difference is enough to cover the transaction costs.
A basic trading strategy would require establishing buy thresholds based on the distribution of underpricing predictions and the ability to invest on all IPOs, which might not always be a possibility. As several theories discussed in [
1] suggest, factors such as higher demand for promising IPOs, laddering practices, or book building strategies by underwriters, are likely to result in higher allocation of bottom performers and lower than desired, if any, of the good ones. This means that the naïve strategy might not be as lucrative in practice as it may seem at first sight. There are many other alternatives that are worth exploring, but they are beyond the scope of this paper. However, the results of the experiments leave the room open for additional work on random forests for IPO trading.
We should note that the reported performance gap between random forests and the other algorithms might be understated due the decision to focus the analysis on variables related to structure of the offerings. This technique combines efficiently strong and weak variables, and it has already been proven to deal with large numbers of variables in financial applications [
39]. Hence, it is likely to profit very significantly from the inclusion of financial ratios and IPOs market indicators. This is something that should be explored in the future.
The results obtained in the experiments support the idea that random forests are suitable in this domain due to the good match, its mentioned characteristics, and the nature of the technique.
5. Summary and Conclusions
IPO underpricing prediction is a domain with some specific characteristics that make it especially challenging. Among them, we could highlight the fact that the set of descriptive variables identified by academic research is limited in their predictive power and mixes both weak and strong predictors. In addition to this, the presence of outliers, that usually take the form of IPOs with extremely high initial returns, adds noise and complicates the process of training models.
In this paper, we suggest that random forests, a technique that, by design, is less sensitive to distortions introduced by the extreme elements in the training sample, could be very useful to perform the task. In order to do that, we test its predictive performance in terms of root mean squared prediction error on a sample of 866 USA IPOs. The approach relied on six variables identified by literature review that were available in commercial databases.
In order to have a meaningful base of comparison, we benchmark the results against eight popular machine learning algorithms: IBK, least median of squares regression, LWL, multilayer perceptron, M5P, M5Rules, radial basis neural networks, and SMO-Regression. This represents different families of predictive algorithms as those based on functions, nearest neighbors, rules, and decision trees.
The outcome of this comparison shows that random forests outperform the alternatives in terms of mean and median predictive accuracy over the 15 repetitions of the 10-fold cross-validation analysis. The technique also provided the second smallest variance and error range among the stochastic algorithms. As an additional side result, we also confirmed the importance of price over the other five predictive variables.
The experimental work also explores the potential of the technique on two practical fronts: as an IPO pricing support tool, and as the core of IPO trading strategies. The usefulness of random forests for both applications is supported by the results. On the one hand, model-based average underpricing is both the lowest among the benchmarked alternatives, and significantly smaller than the actual observed one. On the other hand, the algorithm shows strong capabilities in terms of ranking IPOs according to their potential initial returns.
The above-mentioned results suggest that IPO research would benefit greatly from a wider use of random forests. Possible future lines of work would include replicating the analysis for samples from other countries and extended sets of independent variables. Another promising line would be exploring in depth the potential or random forests to identify a priori hot IPOs and exploiting this knowledge for investment purposes.