A Feature-Based Structural Measure: An Image Similarity Measure for Face Recognition

Featured Application

This work integrates image structural features into a new similarity measure suitable for face recognition with the new merit of recognition confidence.

Abstract

Facial recognition is one of the most challenging and interesting problems within the field of computer vision and pattern recognition. During the last few years, it has gained special attention due to its importance in relation to current issues such as security, surveillance systems and forensics analysis. Despite this high level of attention to facial recognition, the success is still limited by certain conditions; there is no method which gives reliable results in all situations. In this paper, we propose an efficient similarity index that resolves the shortcomings of the existing measures of feature and structural similarity. This measure, called the Feature-Based Structural Measure (FSM), combines the best features of the well-known SSIM (structural similarity index measure) and FSIM (feature similarity index measure) approaches, striking a balance between performance for similar and dissimilar images of human faces. In addition to the statistical structural properties provided by SSIM, edge detection is incorporated in FSM as a distinctive structural feature. Its performance is tested for a wide range of PSNR (peak signal-to-noise ratio), using ORL (Olivetti Research Laboratory, now AT&T Laboratory Cambridge) and FEI (Faculty of Industrial Engineering, São Bernardo do Campo, São Paulo, Brazil) databases. The proposed measure is tested under conditions of Gaussian noise; simulation results show that the proposed FSM outperforms the well-known SSIM and FSIM approaches in its efficiency of similarity detection and recognition of human faces.

1. Introduction

In view of the current issues of terrorism, security in the western world has been heightened, and is becoming an important and challenging task. Surveillance cameras are now common in airports, hospitals, universities, ATMs, banks and anywhere else with a security system. There is an urgent need to find an accurate and reliable automated system which is able to recognize human faces, in order to identify suspicious persons using cameras [1]. Facial recognition has therefore become the focus of current research, and has received significant attention from academics; many techniques and methods for recognizing human faces have been proposed and applied. However, until now there has been no method which offers the required accuracy in all situations. In other words, existing systems still fall far short of the abilities of a human perception system. This challenge is mainly due to factors that affect the features of an image, such as changes in illumination, background, facial expression and head pose. The task of automatic face recognition is therefore a very complex problem; see [2,3,4] for surveys.

In general, there are two classes of face recognition methods: structural and statistical approaches. Structural approaches are based on the extraction of the local features of a face, such as the shapes of the eyes, mouth and nose. These methods suffer from the unpredictability in facial appearance and environmental conditions, e.g., head pose, when a profile image is compared with a frontal image [5]. Conversely, in statistical approaches the complete face region is treated as input data; in other words, global features are extracted from the whole image. The region surrounding the face, including the hair, shoulders and background, is considered to be irrelevant data and may adversely affect the recognition results [6]. Statistical approaches for feature extraction which are based on statistical moment have been used for classification and recognition applications due to their invariance properties [7].

In most facial recognition applications, the similarity between two images is calculated, i.e., using a reference image and a training database image. Several matching algorithms for face and object recognition systems have been designed based on image similarity measurements, such as the structural similarity measure (SSIM), which won an Emmy award for its prediction of the perceived quality of digital images and videos [8].

The main aim of this work is to design an efficient similarity index to resolve the shortcomings of the existing measures in giving high confidence in recognition. The proposed measure combines the best features of the well-known SSIM and FSIM approaches, striking a balance between performance for similar and dissimilar images of human faces. In addition to the statistical structural properties provided by SSIM, edge detection is incorporated as a distinctive structural feature. In addition to confidence, the proposed measure (FSM) gives a reliable similarity between any two images even under noise, in other words, FSM produces maximal similarity when the images are similar, while giving near-zero similarity when the images are dissimilar. These properties gave the proposed measure high ability to recognize face images under noisy conditions, different facial expressions and pose variations. Such properties are highly needed in security applications while checking the identity of a specific face image in a big database.

2. Background

During the last few years, many studies, methods and approaches to similarity and recognition of human faces have been presented to achieve high success rates for accuracy, confidence in identification and authentication in security systems. A significant step in image similarity was presented by Wang and Bovik in 2004 [9], when they proposed the SSIM. This measure is based on the statistical similarity between two images. However, SSIM can give ambiguous results for two different poses, and confusing results in certain cases where it indicates a high similarity for two images which are in fact dissimilar [10].

In an attempt to develop the similarity measures and using them for face recognition; Hu et al. proposed a similarity measure based on Hausdorff distance for face recognition. This measure can provide similarity and dissimilarity information of two objects to compare them such as faces with different illumination condition and facial expression. The measure has a better performance than the measures based on conventional Hausdorff distance and the eigenface approaches [11].

Xu et al. [12] proposed two new operators for face recognition; to find the pixel intensity variation information of overlapping blocks resulted from the original face image. Two factors let the proposed operators work better than the conventional interest operator: the first one is that by taking the relative as the feature of an image block. The second one is that the scheme to partition an image into overlapping allows the proposed operators to give more representation information for the face image.

In 2011, an improved version of SSIM was proposed by Zhang et al. [13]. This measure was called feature similarity index for image quality assessment (FSIM) in an effort to emphasize its use in recognition; this method depends on the low-level features of images. In this measure, the dimensionless and gradient magnitude are the main features, which play complementary roles in characterizing the image. However, FSIM also produces confusing results in certain cases; for example, it may detect a similarity between dissimilar images or a non-trivial amount of similarity between two different poses.

Singh et al. [14] presented a new similarity approach and applied it in face recognition; by combining phase information of wavelet moments and use the real and imaginary components of wavelet moments to describe an image and develop a similarity measure which is invariant under image rotation.

In 2016 Li et al. presented a novel approach for solving the problem of automatic face recognition when the human faces are taken from frontal views with varying illumination and disguise. The approach is based on extracting dynamic subspace of images and obtaining the discriminative parts in each individual to represent the characteristics of discriminative components and give a recognition protocol to classify face images [15].

The topic of 3D face recognition is getting attention. In 2008 a novel deformation invariant image for robust 3D face recognition was proposed by Li et al. [16]. This work is divided into three phases; firstly getting the depth and the intensity of an image from the original 3D facial data. Secondly, geodesic level curves are created by constructing radial geodesic distance image from the depth image. Finally, deformation invariant image is created by evenly sampling points from the selected geodesic level curves in the intensity image. In 2017 Marcolin et al. presented 105 new geometrical descriptors for 3D face analysis. These descriptors created by composing primary geometrical descriptors (for instance mean and Gaussian) and the coefficients of the fundamental forms, and by applying trigonometric functions (for instance sine and cosine) and logarithm to them [17]. Another approach for 3D feature extraction via geometrical analysis is presented in [18]. To the best of our knowledge, 3D face recognition methods haven’t addressed 3D image similarity so far. It is the intention of the Authors to handle this topic soon.

All of these works didn’t address the confidence in recognition. Only the recognition rate has been used as performance measure. Suppose that two measures ($M_1$ and $M_2$) recognized a face image with 100% similarity. This recognition does not mean that the two measures have the same performance. For example, if $M_1$ produces significant similarities between the test image and another group of K database images, then the suspected faces would be not only the one with maximal similarity, but 1 + K of possible faces. Now if $M_2$ produces significant similarity with one correct face while giving trivial similarities with the rest of the database, then $M_2$ is giving the correct answer with more confidence than $M_1$ which gave several confusing faces in addition to the best match. The proposed measure outperforms existing measures by far in giving less confusion while recognizing the best match for a given face image.

The remainder of this paper is arranged as follows: Section 3 describes the design of the proposed FSM approach for use in face recognition. Section 4 presents the experimental results, performance analysis and discussion. Section 5 presents the conclusions.

3. Similarity Measures

Similarity is the strength of the relationship between two images, while a similarity measure is defined as the distance (based on a specific norm) between various data points. The performance of any similarity measure is heavily dependent on the choice of an appropriate distance function for a given dataset. In this work, an efficient measure is proposed; put simply, it combines the essential elements of both the feature similarity and structural similarity measures. Its performance is analyzed in comparison with both the SSIM and FSIM approaches; the results of the proposed measure were better in all cases, even under conditions of noise.

3.1. Overview of SSIM: A Structural Similarity Measure

Automatic detection of the similarity between images is a significant issue; it plays an essential role in image processing due to its importance in many image processing applications such as enhancement, compression and identity checks. The most important step in the development of image similarity techniques was taken in 2004 by Wang and Bovik [9] when they designed the structural similarity measure (SSIM), which considered image distortion as a combination of three factors: correlation, luminance and contrast. This measure is used extensively in image quality assessment and in many image processing algorithms. The basis of this measure is a set of statistical measurements such as mean, variance and co-variance, used to develop a definition for a distance function that can calculate the structural similarity between a test image and training images. The SSIM measure is expressed by the following equation:

$$\rho \left(x,y\right)=\frac{\left(2{\mu }_x{\mu }_y+c_1\right)\left(2{\sigma }_{xy}+c_2\right)}{\left({\mu }_x^2+{\mu }_y^2+c_1\right)\left({\sigma }_x^2+{\sigma }_y^2+c_2\right)},$$

(1)

where $\rho \left(x,y\right)$ represents the similarity between two images $x$ and $y$; $x$ is the reference image, while $y$ is usually a corrupted version of $x$; and ${\mu }_x$, ${\mu }_y,$ ${\sigma }_x$ and ${\sigma }_y$ are the statistical means and variances of images $x$ and $y$, respectively. The variable ${\sigma }_{xy}$ is the statistical co-variance between the pixels in images $x$ and $y$. The constants $c_1$ and $c_2$ are given by $c_1={\left(K_{1}L\right)}^2$ and $c_2={\left(K_{2}L\right)}^2$, where $K_1$ and $K_2$ are small constants and $L=255$ (maximum pixel value). Researchers have confirmed that the values of these constants have little effect on the performance of SSIM [19].

3.2. Overview of FSIM: A Feature Similarity Measure

The feature similarity measure (FSIM) is based on the fact that human visual perception recognizes an image according to its low-level features. FSIM is divided into two parts: the first is the phase congruency (PC), which is a dimensionless measure for the significance of a local structure, while the second is the gradient magnitude (GM). PC and GM play complementary roles in image characterization [13]. The FSIM index between two images $f_1$ and $f_2$ is defined as follows:

$$FSIM\left\{f_1\left(\mathrm{x}\right),f_2\left(\mathrm{x}\right)\right\}=\mathsf{\Phi }\left\{f_1\left(\mathrm{x}\right),f_2\left(\mathrm{x}\right)\right\}=\frac{{{\displaystyle \sum }}_{x\in \Omega }{S}_L\left(\mathrm{x}\right)\times PC\left(\mathrm{x}\right)}{{{\displaystyle \sum }}_{x\in \Omega }P{C}_m\left(\mathrm{x}\right)},$$

(2)

where $\Omega$ represents the whole spatial domain for image pixels, $PC$ is the phase congruency and $S_L$ is a similarity resulting from combined similarity measure for phase congruency $S_{PC}\left(\mathrm{x}\right)$ and similarity measure for gradient $S_G\left(\mathrm{x}\right)$ given by the formula:

$$S_L\left(\mathrm{x}\right)={\left[S_{PC}\left(\mathrm{x}\right)\right]}^{\alpha }\times {\left[S_G\left(\mathrm{x}\right)\right]}^{\beta },$$

(3)

where α and β are parameters used to adjust the relative importance of phase congruency (PC) and gradient magnitude (GM) features, here taken as $\alpha =\beta =1$; and

$$S_{PC}\left(\mathrm{x}\right)=\frac{2P{C}_1\left(\mathrm{x}\right)\times P{C}_2\left(\mathrm{x}\right)+T_1}{P{C}_1^2\left(\mathrm{x}\right)\times P{C}_2^2\left(\mathrm{x}\right)+T_1},$$

(4)

where $T_1$ is a positive constant, inserted to increase the stability of $S_{PC}$ (such a consideration was also included in SSIM), and

$$S_G\left(x\right)=\frac{2G_1\left(\mathrm{x}\right)\times G_2\left(\mathrm{x}\right)+T_1}{G_1{}^2\left(\mathrm{x}\right)\times G_2{}^2\left(\mathrm{x}\right)+T_2},$$

(5)

is the gradient similarity, where $G=\sqrt{G_x^2\left(\mathrm{x}\right)+G_y^2\left(\mathrm{x}\right)}$ is the gradient magnitude; $G_x$ and $G_y$ are partial derivatives of image $f\left(\mathrm{x}\right)$. The phase congruency PC is defined as follows:

$$\mathrm{PC}\left(\mathrm{x}\right)=\frac{\mathrm{E}\left(\mathrm{x}\right)}{\mathsf{ϵ}+{{\displaystyle \sum }}_{\mathrm{n}}{\mathrm{A}}_{\mathrm{n}}\left(\mathrm{x}\right)},$$

(6)

where $\mathsf{ϵ}$ is a small positive constant, and

$$E\left(\mathrm{x}\right)=\sqrt{K^2\left(\mathrm{x}\right)+H^2\left(\mathrm{x}\right)},$$

(7)

where $H\left(\mathrm{x}\right)={{\displaystyle \sum }}_n{o}_n\left(\mathrm{x}\right)$ and $K\left(\mathrm{x}\right)={{\displaystyle \sum }}_n{e}_n\left(\mathrm{x}\right)$, $o_n\left(\mathrm{x}\right)=\xi \left(\mathrm{x}\right)*M_n^e$; $e_n\left(\mathrm{x}\right)=\xi \left(\mathrm{x}\right)*M_n^o$, noting that $M_n^e$ and $M_n^o$ are even and odd symmetric filters on scale $n$, and ‘*’ denotes convolution. The function $\xi \left(\mathrm{x}\right)$ is a 1D signal obtained after arranging pixels in different orientations. The local amplitudes $A_n\left(\mathrm{x}\right)$ are defined as:

$$A_n\left(\mathrm{x}\right)=\sqrt{e_n^2\left(\mathrm{x}\right)+o_n^2\left(\mathrm{x}\right)} ,$$

(8)

where $\mathrm{x}$ is the position on scale $n$.

3.3. The Proposed Measure (FSM)

As discussed above, there are certain shortcomings in the performance of the feature similarity and structural similarity measures, particularly since they produce confusing results in some cases. Both FSIM and SSIM may detect a non-trivial amount of similarity when two images are dissimilar and can give low recognition confidence. Both measures fail to detect similarity under conditions of significant noise.

A new similarity index is proposed here to resolve the shortcomings of SSIM and FSM and to give a more reliable measure of similarity, especially for human face images. This new measure is called the Feature-Based Structural Measure (FSM). On the other front, a new measure for confidence in face recognition is proposed.

FSM combines the best features of the well-known SSIM and FSIM approaches, striking a balance between their performances for similar and dissimilar images. The inclusion of edge detection in FSM presents a distinctive structural feature, in which two binary edge images, $g_x$ and $g_y$, are obtained after edge detection of the original images $x$ and $y$ using Canny’s method [20]. The FSM is given by a rational function, as follows:

$$ℱ\left(x,y\right)=\frac{\left(a+c\right)·R\left(g_x, g_y\right)·\mathsf{\Phi }\left(g_x, g_y\right)+b·R\left(g_x, g_y\right)+e}{\left(a+b\right)·\rho \left(g_x, g_y\right)+c·R\left(g_x, g_y\right)·\mathsf{\Phi }\left(g_x, g_y\right)+e},$$

(9)

where, $ℱ\left(x,y\right)$ represents the proposed similarity between two images $x$ and $y$; usually, $x$ represents the reference image and $y$ represents a corrupted version of $x$; $\mathsf{\Phi }$ represents the feature similarity measure (FSIM); and $\rho$ represents the structural similarity measure (SSIM). The constants are chosen as $a$ = 5, $b$ = 3 and $c$ = 7, while $e$ = 0.01 is added to balance the quotient and avoid division by zero. The function $R\left(x,y\right)$ refers to the global 2D correlation between the images, as follows:

$$R\left(x,y\right)=\frac{{{\displaystyle \sum }}_i{{\displaystyle \sum }}_j\left(x_{ij}-x_{\mathrm{o}}\right)\left(y_{ij}-y_{\mathrm{o}}\right)}{\sqrt{\left[{{\displaystyle \sum }}_i{{\displaystyle \sum }}_j{\left(x_{ij}-x_{\mathrm{o}}\right)}^2\right]\left[{{\displaystyle \sum }}_i{{\displaystyle \sum }}_j{\left(y_{ij}-y_{\mathrm{o}}\right)}^2\right]}},$$

(10)

where $x_{\mathrm{o}}$ and $y_{\mathrm{o}}$ are the image global means. This function is applied here as $R\left(g_x,g_y\right)$ on the new images obtained from the application of edge detection to the original images x and y. The simulation results show that the proposed FSM technique gives better performance than SSIM and FSIM for facial recognition, even under conditions of noise. This excellent performance is due to the rational combination of different approaches (hence different features) with proper weights in Equation (9). The proper weights can control the good/bad features provided by the combined measures.

The only limitation for the proposed measure is the complexity of Equation (9) as compared with the complexity of Equations (1) and (2), where it requires more time. This issue can be alleviated by high-performance computing. However, this is a cheap price for correct recognition, especially in security applications.

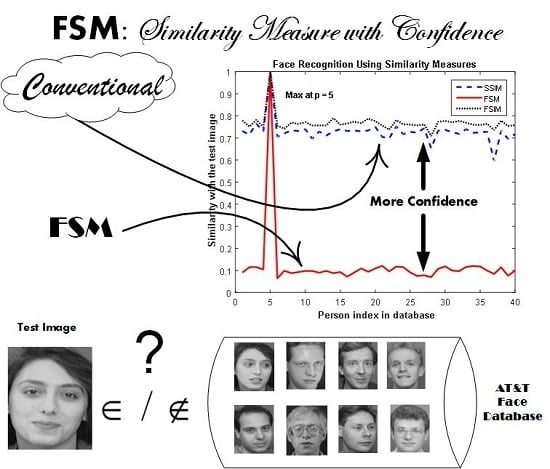
3.4. A Measure for Face Recognition Confidence

The quality of recognition varies from one measure to another; hence, a measure is necessary to evaluate its performance. Here, a measure for the quality of recognition is designed based on the confidence provided by the face recognition method. This confidence indicates the nearness of the similarities to a test image given for the recognized face and the second most likely face from the database.

The similarity between a test image and a database of $N$ face images will produce $N$ similarity numbers, ranging between 0 and 1. These numbers are method-dependent. A cluster of numbers within a small range indicates a reduced confidence. The most important similarities (that should be well apart) are the maximum similarity number (which gives the best match, or recognition result) and the second maximum number, which is associated with confusion. If normalization is applied then the maximum is always 1, while the difference $m$ with the second maximum would vary according to the degree of confusion. The confidence in face recognition at level $k$ of similarity with a specific test image is defined in this work as follows:

$$C_k=\frac{\left(1-k\right)}{n_k},$$

(11)

where $n_k$ is the number of persons with $k$-level of similarity $s_k>k.$

3.5. Discussion

Image similarity measures (for face recognition) didn’t address the issue of confidence in recognition. Only the recognition rate has been used as performance measure. Suppose that two measures ($M_1$ and $M_2$) have recognized a face image (inside a database) with 100% similarity to a reference face image. This recognition does not mean that the two measures have the same performance. For example, if $M_1$ produces significant similarities between the test image and another group of K (a positive integer of) database images, then the suspected faces would be not only the one with maximal similarity, but a number 1 + K of possible faces. Now if $M_2$ produces significant similarity with one correct face while giving trivial similarities with the rest of the database images, then $M_2$ is giving the correct answer with more confidence than $M_1$ which gave several confusing faces in addition to the best match. We will see that the proposed measure outperforms existing measures by far in giving less confusion while recognizing the best match (in a database) for a given face image.

4. Experimental Results and Performance

4.1. Image Database

Most automatic face recognition systems are dependent on a comparison between a given face image (a reference image) and images saved in memory. The face images in memory are represented by a training set saved as a database. In this paper, our training sets are:

• ORL faces images database: AT&T (American Telephone & Telegraph, Inc; New York City, NY, USA) or ORL database this is a well-known database which is widely used for testing face recognition systems. It consists of 40 individuals; each with 10 different images (poses). These images are taken with different levels of illumination, rotation, facial expression and facial details such as glasses. The size of each image is 92 × 112 pixels, with 256 grey levels per pixel [21]. See Figure 1.
• FEI faces images database: FEI database or Brazilian database, it consists of 200 individuals; each with 14 different images (poses). These images are taken at the artificial intelligence laboratory of FEI in Brazil; represented by students and staff at FEI, between 19 and 40 years old with distinct appearance, hairstyle, and adorns. The images in FEI database are colorful and size of each image is 640 × 480 pixels; in our experiment we used 700 images from FEI database for 50 individuals each with 14 poses [22]. See Figure 2.

4.2. Testing

The proposed FSM approach is tested using MATLAB R2015 (from Mathworks Inc., Natick, MA, USA), with a focus on its performance in detecting similarity under noisy conditions. Specifically, the corruption of images under Gaussian noise is considered, due to the fact that this is the main source of noise in many image processing systems. Peak signal-to-noise ratio (PSNR) was used in this test, as follows:

$$PSNR=\frac{L^2}{p_n},$$

(12)

where $L$ is the maximum level of illumination and $p_n$ is the power of the Gaussian noise [23].

4.3. Results and Discussion

The new FSM technique was implemented as per Equation (9), with the well-known measures SSIM as per Equation (1) and FSIM as per Equation (2). These three methods were implemented simultaneously on 1100 images from two datasets; all images of AT&T database and 700 images of FEI database to compare their performance. The distance between the first and second maxima of the similarity curve (peaks) is used for all recognition methods. A greater distance means more confidence in the facial recognition decision. Almost for all cases, the proposed FSM keeps larger difference between the test image and other individuals; better confidence in the recognition process is obtained. Figure 3 shows the poses of the fourth person in the AT&T database, used for testing; Figure 4 shows the poses of the eighth person, also used for testing. Figure 5 shows the poses of the fifth person in FEI database and Figure 6 shows the poses of the fifteenth person in FEI database also used for testing. The reference pose, used as the test image, is indicated. A pose with no significant angle is chosen for the purposes of testing and comparison, although eye-glasses are considered in the first test (see Figure 3), which increases the difficulty of face recognition.

In Figure 7, Figure 8, Figure 9 and Figure 10, the proposed FSM gives better performance in terms of recognition confidence. In spite of the fact that the other measures SSIM and FSIM correctly decide the proper person with maximum similarity, they give low confidence in their decision because there are many cases of distrust (big similarities with wrong persons) in their decisions (similarities); this is a big challenge when we employ these measures in security recognition tasks. FSM gives more confidence to decide the proper person from a database.

Figure 11 shows the performance of similarity measures using person No. 15 in FEI database. Pose 8 is the Reference Image, while a different pose (pose 10) is used for testing for all database images (including the target person). FSIM fails, while confidence of SSIM, and FSM is 0.0364, 0.12 respectively.

Figure 12, Figure 13, Figure 14 and Figure 15 we simulated the confidence measure as per Equation (11) to show the efficiency of the proposed measure (FSM) in giving the highest confidence versus the well-known SSIM and FSIM.

In Figure 16, Figure 17, Figure 18 and Figure 19, the proposed measure FSM produces near-one (maximal) similarity for similar images under Gaussian noise, while giving near-zero similarity when the images are dissimilar. The other measures SSIM and FSIM gave non-trivial amounts of similarity when the two images are quite different, which indicates a shortcoming in these measures.

Figure 7 and Figure 8 show the results of the similarity test on person No. 4 and person No. 8 in AT&T database. The similarity test between the reference image and other images in database, where for the 10 poses for each individual the maximum similarity between the rest of the poses is considered.

Figure 9 and Figure 10 show the results of the similarity test on person No. 5 and person No. 15 in FEI database. The similarity test between the reference image and other images in database, where for the 14 poses for each individual the maximum similarity between the rest of the poses is considered.

The performance of the proposed measure was also tested when the image was corrupted with Gaussian noise. Peak signal-to-noise ratio (PSNR) was utilized in this case, as discussed above for Equation (12); this was then compared with the structural similarity measure (SSIM) and feature similarity measure (FSIM). The results show the effectiveness of FSM in similarity and face recognition. Figure 16 and Figure 17 show the performance of FSM for similar images under Gaussian noise, while Figure 18 and Figure 19 show the performance of FSM for dissimilar images under Gaussian noise. Similar images from AT&T database corrupted with Gaussian noise were tested; these are shown in Figure 16a. The performance of FSM (represented by Equation (9)) as compared to that of SSIM and FSIM is shown in Figure 16b.

Similar images from FEI database corrupted with Gaussian noise were tested; these are shown in Figure 17a. The performance of FSM (represented by Equation (9)) as compared to that of SSIM and FSIM is shown in Figure 17b.

The results of comparing another face image are shown in Figure 18a. Another face image was used from AT&T database as the dissimilar image. Figure 18b shows the performance of FSM (represented by Equation (9)) as compared to SSIM and FSIM for conditions of Gaussian noise.

In [24] it is shown that higher-order correlations can lead to better performance. It is the intention of the authors to extend this work in the near future towards a higher-order correlative measure, analogous to that in Equation (9).

The results of comparing another face image are shown in Figure 19a. Another face image was used from FEI database as the dissimilar image. Figure 19b shows the performance of FSM [represented by Equation (9)] as compared to SSIM and FSIM under Gaussian noise.

5. Conclusions

An efficient similarity measure known as the feature-based structural measure (FSM) is proposed here, based on a rational functional and combining the well-known algorithms of the structural similarity measure (SSIM) and feature similarity measure (FSIM) with Canny edge-detected versions of two images. This measure enhances the best features of both SSIM and FSIM in addition to the distinctive structural feature provided by Canny’s approach. It is shown here that FSM outperforms the conventional SSIM and FSIM in its ability to detect the similarity (that is, high similarity results) among similar faces, even under significantly noisy conditions; it also avoids the detection of similarity in the case of dissimilar faces, which is a major shortcoming of the existing FSIM and SSIM approaches. A measure for confidence in face recognition has also been proposed as a performance measure for face recognition methods. In facial recognition tasks, FSM gives higher recognition confidence than existing measures. In addition to confidence, the proposed measure (FSM) gives a reliable similarity between any two images even under noise, in other words, FSM produces maximal similarity when the images are similar, while giving near-zero similarity when the images are dissimilar. These properties gave the proposed measure high ability to recognize face images under noisy conditions, different facial expressions and pose variations. Such properties are highly needed in security applications while checking the identity of a specific face image in a big database. In this work, global analysis of facial images has been used, in which the complete facial region is taken as input data and treated simultaneously. Local face analysis has been shown to play an important role in improving face recognition performance. The authors intend to extend their previous work on local analysis to improve the performance of the above measure. In addition, the Authors suggested a call for 3D image similarity, a new topic that they will handle soon.