Contact Pressure and Strain Energy Density of Hyperelastic U-shaped Monolithic Seals under Axial and Radial Compressions in an Insulating Joint: A Numerical Study

Abstract

In insulation joints, elastomeric U-shaped monolithic seals (UMSs) are replacing O-ring systems because of their enhanced sealing capabilities for the oil and gas industries. UMSs are compressed axially during assembly and radially when pressurized in operation. The reliability of UMSs due to the displacement imposed during assembly and the internal pressure in operation is influenced by the axial compression ratio, thickness ratio (TR), and geometric complexity. In this study, the hyperelastic behavior of elastomeric UMSs under axial and radial compressions is investigated using axisymmetric finite-element analysis. Twelve examples of UMSs with three geometric restraints (open grooves on both sides (type 1), an open groove on one side only (type 2), and no groove (type 3)) and four thickness ratios (TR = 0.25, 0.50, 1.00, and 1.50) are evaluated. To analyze nonlinear elastomeric materials, neo-Hookean constitutive equations are applied and the UMSs are considered as being a nearly incompressible hyperelastic material with a Poisson’s ratio of 0.499. The failure and detachment risks of UMSs are analyzed in terms of the equivalent stress, gap distance, contact pressure, and strain energy density. It is advantageous that the smaller the TR, the smaller the stress distribution. However, the generation of broader detachment regions is observed. Type 1 symmetrically shows the lowest stress distribution and the smallest detachment region, whereas type 3 symmetrically shows the highest values. Type 3 (TR = 0.25) shows the broadest detachment region in the arc-length range from −15.7 to 15.7 mm, whereas the largest gap of 0.7 mm is observed in type 2 (TR = 0.5). For all types, the detachment region disappears completely at TR = 1.0 or higher, which implies that full sealing is occurring. The average contact pressure increases exponentially during axial compression (in assembly) and linearly during radial compression (in operation). The largest contact pressure of 31.5 MPa is observed in type 3 (TR = 1.5), while the lowest is observed in type 1 (TR = 0.25). As for the strain energy density, type 3 at TR = 0.25 shows the largest increase in the strain energy density with 1.75 MJ/m³, while type 1 shows the most stable values of all cases. In conclusion, the lowest risk of failure of a nonlinear hyperelastic UMS was investigated numerically with minor equivalent stress and detachment region with higher contact pressure, which can be taken into account to ensure the reliability of the UMS.

1. Introduction

An unexpected failure of the sealing system in an insulating joint can create serious problems in oil and gas pipelines. Insulating joints are critical components installed in underground natural-gas and oil pipelines. Installed at appropriate intervals between the pipes, insulation joints can reduce the amount of current flowing in the pipelines and maintain the electrical potential difference between pipe sections, thereby preventing pipe corrosion due to electrical or chemical reactions and increasing the service life of pipelines. Furthermore, they can provide electrical protection from the risk of explosion by static electricity or lightning.

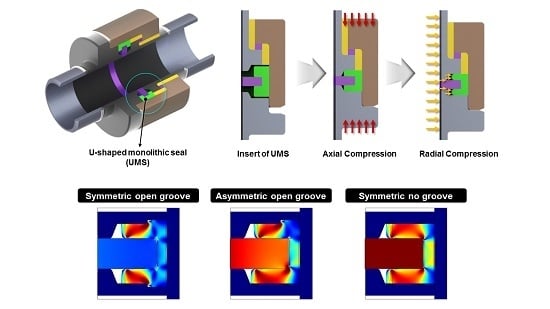
Elastomeric O-ring seals are widely used in various environments and surface conditions because they can provide sealing in many static or dynamic applications at industrial sites. In particular, O-ring sealing systems have traditionally been used in insulating joints. Figure 1 shows a three-dimensional (3D) schematic, with a 1/4 cross-sectional cut, of an insulating joint based on an O-ring sealing system. To structurally separate the external pipes that are connected at either end, insulating spacers (laminate thermoset or high-density epoxy resin and glass-fiber shape-composite material) and insulating fillers (epoxy resin or cold curling resin), which consist of nonmetal materials, are installed inside the pipelines. Elastomeric O-ring seals (Viton rubber, fluorine rubber, or nitrile butadiene rubber) are mounted to prevent leaks of gas or oil between the metal and insulation components.

To prevent undesired failures of a sealing system, a number of studies have been conducted on elastomeric O-ring sealing systems using finite-element analysis (FEA). These have been focused on predicting the behavioral characteristics of O-ring seals in diverse and complex compression and pressure environments [1]. Wu et al. [2] suggested an analytical stress-distribution model to describe the stress distribution of O-ring seals by adapting two-stress complex functions. The sealing performance of O-ring seals was described by the analytic stress-distribution functions under various squeeze rates and internal pressures. Chen et al. [3] introduced end-face deformation of the combined contact model of the flexible ring and O-ring based on numerical simulations. In the combined seals, fractional compression of the O-ring and the elasticity modulus of the flexible ring had the largest effect on the end-face deformation. Yamabe et al. [4] exposed a rubber O-ring to cyclic high-pressure hydrogen gas to investigate the fracture behavior. The crack damage due to degradation of the mechanical properties of the O-ring was characterized in terms of the hydrogen pressure, using a developed durability tester. To summarize the previous studies, the sealing capability of O-rings depends on:

• the magnitude of stress acting on the O-ring;
• the contact stress between the O-ring and the wall;
• the contact area (or length) for sealing between the O-ring and the wall.

O-ring seals used in oil and gas pipelines are exposed to extreme environments such as large changes in temperature, pressure, and conveyed fluid [5]. Furthermore, depending on the geometry of O-ring seals, they are exposed to highly complex operating conditions as they are compressed and constrained. In such situations, it has been reported that leakage can start when the pressure acting on an O-ring is greater than the contact stress or when there is a gap in the contact length [6]. In this regard, even though O-ring sealing systems have been used extensively in industry, they have the following shortcomings:

• Their resistance to high-pressure environments is limited because they have low contact stress because of the small cross-sectional area of the O-rings.
• They are susceptible to damage such as explosive decompression, swell-ups, and tear-off because they cannot effectively withstand when subjected to pressure cycles and fast pressure changes because of the geometrical limitation of the O-rings.
• They cannot maintain proper mechanical sealing if the insulating joints undergo deformations (e.g., bending, elongation, compression, or torsion) from external loads because of the short contact length of the O-rings.

To resolve the disadvantages of O-rings, some different geometries have been proposed by researchers. Cui et al. [5] applied nonlinear theory to investigate the performance of Y-ring seals under the influence of hydraulic pressure. Based on the failure criterion (i.e., von Mises stress), the location showing the maximum contact stress and the largest deformation was suggested, which could cause aggravated wear. Bernard et al. [6] investigated the contact behavior of an X-ring seal under a uniform squeeze rate and internal pressure. Both contact and internal stresses were analyzed using the hybrid photoelastic experimental method, in which the sealing performance was investigated based on the maximum shear failure criterion. Zhang et al. [7] performed FEA to obtain distribution curves of sealing contact pressure of bud-shaped composite sealing rings in a diverse pressure environment. The analytic 3D pressure distributions were compared experimentally using a pressure-sensitive film. In spite of their improved sealing performance compared to O-rings, these methods still have limitations over a broad range of operating conditions and surface finishes because of the geometric constraints.

Another solution has recently been introduced to improve the disadvantages of O-ring sealing systems, namely the U-shape monolithic seal (UMS) or double seal. The UMS shows a high contact stress, with a substantially longer contact length and a larger cross-sectional area compared to conventional O-ring systems. Accordingly, it has the potential for widespread use, irrespective of the size and pressure ranges of pipelines. The structural advantages of the UMS are that it can maintain sealing even if subjected to structural deformations such as bending, elongation, compression, or torsion. Although the application scope of UMSs has been increasing, their exact behavior in the manufacturing process and different pressure environments is not yet fully understood for the following reasons. Firstly, compared to conventional O-ring sealing systems, because of a more complex geometry and highly restrained deformation conditions, it is difficult to predict analytically the nonlinear hyperelastic behavior of a UMS. In the case of hyperelastic materials, the dramatic change between softness and stiffness under various loading conditions because of the Mullins effect makes analysis difficult. Secondly, the bulk moduli of UMSs are very large compared to their shear moduli. As a result, they show incompressible behavior, thus causing a sharp increase in stress compared to the strain in a compression environment. Thirdly, they exhibit different behaviors depending on whether they are in a uniaxial, biaxial, or planar axial deformation state [8,9,10,11]. Many researchers have proposed various mathematical constitutive models to predict the nonlinear response of hyperelastic materials under various deformation conditions [12,13,14,15,16]. Thus, it is necessary to predict the behavior of nonlinear hyperelastic UMS by a finite-element method (FEM) in the design stage, which can economically and effectively realize the integrity of the UMS.

The aim of the present study was to analyze the hyperelastic behavior of a UMS numerically for various compression and pressure conditions, from assembly to use, in insulating joints. To overcome the difficulty of analyzing the nonlinearity of the UMS, a nonlinear constitutive equation was applied and a two-dimensional (2D) axisymmetric model was introduced to the analysis. Under different thickness ratios of the UMS and various geometric constraints of the housing in which the UMS were installed, the contact stress, von Mises stress, contact length, and strain energy density were analyzed in axial and radial compression environments. Because the nonlinear behavior of the elastomeric UMS could be taken into account in this study, methods to optimize the UMS at the design stage could be suggested by taking minor equivalent stresses with higher contact stress into account.

2. Materials and Methods

2.1. Hyperelastic Sealing Material

In this study, the production of a UMS using FKM, one type of rubber class designated in American Society for Testing and Materials (ASTM) D1418, as a hyperelastic material was considered. FKM is a sealing material that is widely used in the oil and gas industries [17]. It consists of 80% or more of fluoroelastomer, which is a synthetic rubber with very high thermal and chemical stability. Unlike Hooke’s law, which is used for general linear elastic behavior, a hyperelastic material shows nonlinear behavior in its stress–strain relationship.

Therefore, the stress–strain relationship of a hyperelastic material is defined using the strain energy density function, W. By differentiating the strain energy density function with respect to strain, a corresponding stress component can be obtained. The strain energy density function can be expressed in various ways: statistics-based, invariant-based, or stretch-based mechanics. Various hyperelastic material models are introduced in the literature [18]. In this study, the invariant-based hyperelastic material model based on continuum mechanics was applied. The general form of an isotropic hyperelastic material model can be expressed as follows [18,19]:

$$W={{\displaystyle \sum }}_{i, j=0}^{\infty }{C}_{ij}{\left(I_1-3\right)}^i{\left(I_2-3\right)}^j,$$

(1)

where $I_1$ and $I_2$ are the first and second invariants of the stretch tensor, respectively, and $C_{ij}$ is the material constant. Although hyperelastic materials are theoretically incompressible, they actually show a slightly compressible behavior in reality. To implement this behavior into the analysis, the strain energy density was assumed to be composed of two different strain energy densities [18,20,21,22]:

$$W=W_{distortion}+W_{dilatation},$$

(2)

where $W_{distortion}$ is the distortional (or shear) strain energy density, representing the constant volume in shape, and $W_{dilatation}$ is the dilatational (or hydrostatic) strain energy density, indicating the change in volume. It is noted that the distortional energy density, $W_{distortion}$, is related to the tangential component of the stress vectors, showing a linear correlation with the first invariant $I_1$. The volumetric dilatation of isotropic materials can be affected only by the normal component of the stress vectors. Thus, the volumetric strain energy density, $W_{dialation}$, is related to the compressibility.

Nonlinear elastomeric materials are generally known to have very high bulk moduli compared to shear moduli. This implies that their volume changes very little, even if the material is elongated or shrunk in the event of shear deformation. In other words, the material shows almost-incompressible behavior under volumetric compression. If an elastomeric material is assumed theoretically to be completely incompressible (bulk modulus $k=\infty$), with complex shape or load conditions, it can be difficult to obtain calculated results because of element locking when predicting the material behavior through numerical analysis [17,23]. However, this ideal condition is not found in practice, and even if the material is theoretically incompressible, it shows slightly compressible behavior. Therefore, the compressibility of the UMS was defined as nearly incompressible, and the Poisson’s ratio was set at 0.499.

The nonlinear elastomeric behavior of FKM was described using the neo-Hookean model, which is one of the simplest hyperelastic models. For numerical analysis, in the case of the neo-Hookean constitutive equations, the Poisson’s ratio of 0.499 can be applied to describe the nearly incompressible behavior of an elastomeric material [1,17]. In addition, this model shows very good conformity with experimental values up to approximately 40% strain under uniaxial tension [1,17]. Modifying Equation (2) using the neo-Hookean model, the strain energy density can be expressed as follows [20]:

$$W=\frac{1}{2}G\left(I_1-3\right)+\frac{1}{2}\lambda {\left[\ln (J_{el})\right]}^2-\mu \ln (J_{el}),$$

(3)

where G is the shear modulus, $I_1$ denotes the first strain invariant of the elastic right Cauchy–Green deformation tensor $I_1\left(\overline{C_{el}}\right)$, and $\lambda$ and $\mu$ are the first and second Lamé parameters, respectively. $J_{el}$ is the volume change ratio; note that volume change due to thermal effects was not included. Considering the material to be nearly incompressible, the strain energy density function can be written using the isochoric invariant $I_1\left(\overline{C_{el}}\right)$ as follows [20]:

$$W=\frac{1}{2}G\left(\overline{I_1}-3\right)+ \frac{1}{2}\kappa {\left(J_{el}-1\right)}^2,$$

(4)

where $G$ is the shear modulus of the material and $\kappa$ is the bulk modulus. The material was assumed to be isotropic. A bulk modulus of $k=10$ GPa was applied for the elastomeric material [17,24].

2.2. Axisymmetric Model

Figure 2a shows a 3D schematic, with a 1/4 cross-sectional cut, of an insulating joint mounted with a UMS. Considering the cylindrical geometry of the UMS, the insulating joint was configured as a 2D axisymmetric model. The center of the UMS was constrained by a rigid insulating spacer, while the outside surface was surrounded by the left and right pipe pups and the retainer. For the models, a second-order Lagrangian element was applied to discretize the geometry.

For the model analyzed in this study, as shown in Figure 2c, three geometric housing restraints in which the UMS could be installed were considered: open grooves on both sides (type 1), an open groove on one side only (type 2), and no groove (type 3). Type 1 represents a symmetric open groove (SOP), type 2 an asymmetric open groove (ASOP), and type 3 a symmetric non-groove (SNO). In addition, values of the UMS thickness ratio (TR) of 0.25, 0.50, 1.00, and 1.50 were considered to examine the behavior of the UMS according to the thickness difference for each type. In this study, the TR is defined as follows:

$$\mathrm{TR}=\frac{t_{body}}{t_{leg}},$$

(5)

where $t_{leg}$ denotes the thickness of the UMS leg, which was fixed to 15 mm. $t_{body}$ represents the thickness of the UMS body; values of 3.75, 7.50, 15.00, and 22.50 mm were applied to realize TR = 0.25, 0.50, 1.00, and 1.50, respectively. The other geometric dimensions were applied with identical conditions to all 12 cases.

The axial compression of a UMS during assembly and its subsequent radial compression by internal pressure were implemented numerically in this study. Figure 3a shows an initially inserted UMS in the insulating joints prior to assembly. Figure 3b indicates the axially compressed UMS by axial displacement during assembly. The axial compression of the UMS was conducted until the UMS leg was compressed from 0% to 40% in thickness in intervals of 10%. During assembly, the UMS was compressed symmetrically by the left and right displaced pipe pups while the retainer ring remained stationary. The insulating spacer in the middle of the UMS was allowed with radial deformation. After assembly, the insulating joint was under radial compression by the internal pressure during operation, as shown in Figure 3c. The internal pressure was applied gradually from 0 to 10 MPa in intervals of 2.5 MPa. The results were analyzed in terms of the stress distribution, contact stress, gap distance, and strain energy density after each step.

2.3. Numerical Analysis Procedure

The bulk modulus of the UMS was considered to be 10 GPa with a Poisson’s ratio of 0.499. Subsequently, its Young’s modulus and Lamé’s parameters were derived. For the pipe pups and the retainer ring, made from ASTM A596-F65, Young’s modulus and Poisson’s ratio were 201 GPa and 0.3, respectively. The insulating spacer, ASTM D709-G10, was chosen with Young’s modulus of 17.2 GPa and Poisson’s ratio of 0.36. All the materials were assumed to be homogeneous and isotropic.

The analysis was performed in two stationary steps. Firstly, axial compressive displacement was applied to examine the nonlinear hyperelastic behavior of the UMS under axial compression during assembly. The constrained displacement condition was applied, and the UMS was compressed gradually at 10%, 20%, 30%, and 40% of the thickness of the UMS leg, $t_{leg}$. As a result, the pipe pups were displaced by 1.5, 3.0, 4.5, and 6.0 mm, respectively. Secondly, internal pressure was applied to the already-compressed UMS to examine the nonlinear hyperelastic behavior of the UMS under radial compression during operation. The pressure was increased gradually to 2.5, 5.0, 7.5, and 10 MPa, respectively. To achieve more rigorous and accurate solutions, an adaptive meshing technique was applied.

Numerical techniques to solve nearly incompressible hyperelastic finite-element models are known to be quite complicated because the Poisson’s ratio ν is close to 0.500. Thus, in the present analysis, a parametric continuation solving technique was applied to improve the convergence of the results during axial and radial compressions due to the imposed displacement during assembly and internal pressure in operation, respectively. Contact conditions were applied to the inner surface between the UMS and insulating spacer, the outer surface between the UMS and one pipe pup, the outer surface between the UMS and the other pipe pup, and the outer surface between the UMS and retainer ring.

The friction between the UMS and other parts, including the pipe pups, retainer ring, and insulating spacer, was applied as contact boundary conditions. Because of the deformable-to-rigid contact conditions between the UMS and other components, it was important yet difficult to analyze the forces transferred across the contact area. We consider both normal and shear stresses transmitted across the contact surfaces. An isotropic spring foundation with spring constant $k_{tot}$ was applied to stabilize the unconstrained contacts, which were gradually eliminated during auxiliary pressure sweeps.

To achieve smooth and precise results, quadrilateral and second-order Lagrangian mesh elements were used to discretize the axisymmetric geometry. A mesh optimization procedure was conducted until the smallest change in the errors became less than 0.1% as the results converged. The minimum and average element qualities to define the mesh distribution were maintained over 0.200 and 0.700, respectively. The results of the FEA are presented in terms of equivalent stress, contact pressure, gap distance, and strain energy density. The correlations among the results are also analyzed.

3. Results and Discussion

3.1. Deformation and Equivalent Stress under Axial Compression

Based on an axisymmetric FEA analysis, the sealing behavior of the UMS during assembly and the loading conditions are investigated. During assembly, the UMS housed in its surrounding parts was subjected to axial compression by the displacement of the pipe pups. Figure 4 shows the von Mises equivalent stress distributions with the deformed shape of the UMS due to the applied axial displacement up to 8 mm from the left and right pipe pups, which corresponds to a compression ratio of 40%. The deformation scale was set to 1:1 for a true description of the shape.

Because of its near incompressibility, the UMS was deformed by an amount that was equal to the amount of compressed volume by the imposed axial displacement during assembly, and a gradual filling of the space that was empty before compression could be confirmed in general. However, the deformation of the UMS showed different trends according to type and TR. In type 1, the open grooves on both sides, which were empty before compression, were filled first and then the empty space in the leg was subsequently filled. In type 3, which had no open groove, the empty space of the leg was filled the most and it showed the largest deformation among three types. In type 2, the leg with an open groove and the leg with no open groove showed trends similar to the deformations of types 1 and 3, respectively, resulting in asymmetrical deformations. Within the same type, a greater deformation was generated as the TR and the UMS volume increased. The greatest deformation was observed at TR = 1.50.

Together with the deformation of the UMS, the change in the von Mises equivalent stress of the UMS due to axial compression during assembly was examined. In general, the larger the UMS deformation, the greater the distribution of von Mises stress. Type 1 showed the lowest stress distribution, whereas type 3 showed the highest stress distribution. Within the same type, the deformation and stress distributions were symmetrical when the geometric restraints were symmetrical under the same TR conditions, as was the case for types 1 and 3. However, asymmetric deformation and stress distribution occurred in the asymmetric geometric restraint of type 2.

In the case in which the stress distribution acted on the UMS leg region, the same stress concentration was observed at the end where the inner surface of the UMS met the insulating spacer (see circles a and b in Figure 4), regardless of the type. In type 1 with open grooves on both sides, stress concentration was also observed at the corner where the outer surface of the UMS met the open groove (see circles c and d in Figure 4). In type 3 with no open groove, a stress concentration was observed in the inner corner where the inner surface of the UMS met the insulating spacer (see circles e and f in Figure 4). In type 2, the characteristics of types 1 and 3 were observed asymmetrically in each leg. Regardless of the type, as the TR increased, the stress distribution acting on the UMS leg and body regions gradually increased. The greater the TR in axial compression, the greater the compressive force in the UMS. This was because the increased compressive force could not contribute to the volume compression of the nearly incompressible UMS, and most of the imposed forces affected the distortion of the UMS.

As the von Mises’ equivalent stress in the UMS gradually increased, the stress was transmitted to the insulating spacer that was in contact with the inner surface of the UMS, causing an increased stress in the insulating spacer. This increase in stress was large enough to cause deformation of the insulating spacer (TR = 1.50 for type 2, and TR = 1.00 and 1.50 for type 3). This phenomenon occurred because the stiffness of the insulating spacer was the lowest among the surrounding parts of the UMS.

3.2. Contact Pressure and Gap Distance under Axial Compression

Contact pressure is one of the most important variables for distinguishing the sealing capacity of a sealant. The distribution of the contact pressure along the outer area of a UMS was investigated. As shown in Figure 5, the contact-pressure distributions along the interface between the outer area of the UMS and the surrounding area were compared using line profile plots.

In general, the contact pressure tended to increase as the TR increased. Figure 5a,c show symmetrical changes in contact pressure around the arc length at 0 mm, whereas Figure 5b shows asymmetric changes in contact pressure. Type 1 showed a narrow and sharp increase in contact pressure because of the geometrical effect of the open grooves (Figure 5a). In particular, the contact pressure increased to its highest value of 43.8 MPa at TR = 0.50. Type 3, with no open groove, showed a wide and slow increase in contact pressure at both ends of the UMS, with its highest value of 47.1 MPa at TR = 1.50 (Figure 5b). Type 2 showed the characteristics of both types 1 and 3. The leg with an open groove showed a sudden increase in contact pressure, with a maximum value of 43.5 MPa at TR = 0.25, whereas the leg with no groove showed a gradual increase, with its highest value of 32.5 MPa at TR = 1.50.

Using the stress–strain curve suggested in the literature [25], the approximate stress of the 40%-deformed FKM material was experimentally reported to be about 1.5–2.0 MPa at constant volume assumption. Referring to the suggested equations in another literature [1], it was reported that when elastomeric seals were compressed by 40%, the contact pressure of the axially and radially restrained grooves would exponentially increase by about 20–25 times greater than those of the unrestrained geometry. Thus, taking these references together, one can estimate that contact pressure obtained in this study was likely to be about between 30.0 and 50.0 MPa for validity, which corresponded to the results shown in Figure 5. In addition, as shown in the literature, the exponential behavior of elastomeric materials under compressive condition was consistent with our findings.

In Figure 5, particular intervals showing 0 MPa of contact pressure exist in the arc-length range from −22.5 to 22.5 mm, which corresponds to the UMS body area. This implies that there was no contact pressure because the outer surface of the UMS was detached from the surrounding surface of the retainer. To examine the detachment characteristics in more detail, further analysis was conducted on the gap-distance profile, as shown in Figure 6.

In the case of type 1, as shown in Figure 6a, a symmetric detachment region occurred in the arc-length section from −10.8 to 10.8 mm at TR = 0.25, with a maximum gap of 0.12 mm. As the TR ratio increased to 0.5, the detachment region reduced from −6.2 to 6.2 mm, with a decreased gap of 0.03 mm. In the case of type 2, as shown in Figure 6b, the gap was the largest of the three types. Because of the asymmetric geometry of type 2, the detachment region was distributed asymmetrically. The detachment region and the gap were broad and large in the direction in which there was no open groove. On the other hand, they were narrow and small in the direction where there was an open groove. The broadest detachment region was from −16.2 to 10.1 mm at TR = 0.25, with the largest gap of 0.7 mm at an arc length of 7.3 mm. At TR = 0.5, the detachment region decreased slightly from −15.8 to 8.2 mm, with a reduced gap of 0.46 mm. In the case of type 3, as shown in Figure 6c, the detachment region was the broadest of the three types. At TR = 0.25, the symmetrical detachment region was the broadest from −15.7 to 15.7 mm, with a maximum gap of 0.6 mm at the arc length of 7.3 mm. The detachment region and gap decreased gradually at TR = 0.5.

Type 1 showed the best contact with the retainer ring at TR = 0.25, and the detachment was small and narrow. However, types 2 and 3 showed a significant detachment region. As the TR increased, the detachment region tended to decrease. At TR = 0.50, the detachment of type 1 disappeared almost completely, but the detachment regions of types 2 and 3 were still observed broadly. In particular, the detachment region of type 2 was unstable because of its asymmetrical geometry. For all types 1, 2, and 3, the detachment disappeared completely at TR = 1.0 or higher, which implied that full sealing was occurring. It appeared that unstable contact at the retainer was observed at TR = 0.25 as deformed wrinkles that were generated during axial compression because of the thinner UMS and its lower stiffness. This phenomenon caused a large deformation in the UMS with no open groove or asymmetric grooves during compression.

3.3. Deformation and Equivalent Stress under Radial Compression

Figure 7 shows deformations and equivalent stress distributions when an internal pressure of 10 MPa was applied to a UMS that had been compressed axially by 40% during assembly. Among the 12 cases in total, the UMS deformation and stress distribution at TR = 0.5 are plotted in Figure 7 as representative examples. Compared to Figure 4, after an internal pressure was applied to the axially compressed UMS, almost no deformation was observed, but the stress distribution was increased. This change of stress distribution was the lowest in type 1 and the largest in type 3. In particular, type 3 showed that the von Mises stress increased significantly in the UMS body region. Furthermore, the stress was transmitted to the insulating spacer with the smallest stiffness among the surrounding surfaces and caused changes in the deformation and stress.

In Figure 6, types 2 and 3 show large detachments in the UMS body region at TR = 0.25 and 0.50 during the 40% axial compression. However, in Figure 7, TR = 0.5 shows stable contact with almost no gap distance after radial compression, regardless of the type. The radial compression caused by internal pressure could enhance the sealing capacity of the UMS by reducing the gap distance. Furthermore, as the UMS was pressurized radially, the empty space in the open groove was filled to almost no gap. In the radial compression environment by internal pressure, types 1 and 3 maintained symmetric deformation and equivalent stress distributions, whereas type 2 showed asymmetric distributions.

3.4. Average Contact Pressure from Axial to Radial Compression

In Figure 8, the change in the average contact pressure is presented as a function of both axial compression, due to imposed displacement, and radial compression due to internal pressure. The contact-pressure changes are plotted and analyzed for compression ratios of 10%, 20%, 30%, and 40% during assembly and internal pressures of 2.5, 5.0, 7.5, and 10 MPa during operation. Overall, the average contact pressure increased exponentially as the axial compression increased up to 40% during assembly. By contrast, it increased linearly as the radial compression increased up to 10 MPa during operation.

As shown in Figure 8, type 3 showed the largest contact pressure at all TRs, whereas type 1 showed the lowest contact pressure. In the case of type 1, the contact pressure did not change rapidly under axial compression and internal radial pressure, even when the TR increased. At an internal pressure of 10 MPa, type 1 showed contact pressures of 15.5 and 19.0 MPa at TR = 0.25 and 1.50, respectively. However, in the case of type 3, the contact pressure increased sharply with increase of TR. The maximum contact pressure at TR = 1.50 was observed as 31.5 MPa, about 1.5 times greater compared to type 1. This observed difference between types 1 and 3 could be caused by the effect of the open groove.

3.5. Average Strain Energy Density from Axial to Radial Compression

Similar to Figure 8, Figure 9 shows the average strain energy density as a function of the axial compression and the radial compression. The strain energy density represents the energy stored in an object per unit volume. When external forces are applied to an object, the energy given to the object from the outside is stored as potential energy inside the object. Since the strain energy density is not evenly distributed in an object, the mean value per unit volume was used for analysis in this study.

In general, the average strain energy density increased exponentially with increasing axial compression, and then linearly with increasing radial compression. However, the strain energy density showed a different behavior compared to the contact pressure during radial compression. As shown in Figure 9, types 1 and 3 showed the largest difference in the strain energy density at TR = 0.5, unlike the contact pressure in Figure 8, and the difference between the two values tended to decrease gradually as TR increased. Of all cases, type 3 at TR = 0.25 showed the largest increase in strain energy density. For example, at an internal pressure of 10 MPa, the strain energy density of type 3 at TR = 0.25 is 1.75 MJ/m³ in Figure 9a. During radial compression, the strain energy density of type 3 tended to decrease gradually as TR increased to 1.00 and 1.50. In contrast, in the case of type 1, the maximum values were in the range of 0.9–1.0 MJ/m³ at TR = 0.25–1.00, showing no large changes in strain energy density during radial compression.

As mentioned above, the strain energy density can be divided into dilatational and distortional strain energies. The distortional strain energy density is related to the von Mises’ failure criterion. In other words, a ductile material could fail if the distortional strain energy density exceeds a critical value, which, in the present case, can vary according to the design criteria, such as the safety factor, yield stress, or ultimate tensile strength. Here, under the four TR conditions, type 1 shows the lowest values of strain energy density for all cases, which implies the lowest risk of material failure.

In this study, critical features such as equivalent stress, gap distance, and contact pressure were determined during both assembly and internal pressurization. It was confirmed that axial compression during the assembly process plays an important role in an exponential increase of critical values related to the reliable sealing capacity of the UMS system. Radial compression during operation caused linear changes in the above values. The factors required for the sealing system to maintain its features are no failure and no detachment. These could be predicted through the equivalent stress distribution, gap distance, contact pressure, and strain energy density. Therefore, the major conditions for determining the stability of a UMS system can be suggested as follows:

• the smallest stress distribution;
• the narrowest and smallest detachment region at low TR;
• the most stable values of contact pressure and strain energy density for changes in TR, and
• no deformation in the insulating spacer even at high TR.

Considering these conditions in general, type 1 with its symmetric open grooves showed the best results. However, type 1 is limited by the rapid concentration of stress on the open groove. To solve this problem, the change in geometry near the open groove should be applied more smoothly through chamfering, etc. In other words, the stress peaks of an elastomeric UMS that is to be subjected to mechanical loads could be reduced by adapting the design of the component accordingly.

4. Conclusions

The mechanical behavior of a nonlinear hyperelastic UMS during axial and radial compressions was analyzed using 12 different axisymmetric numerical analysis models. The axial compression during assembly was confirmed to be the most important variable in determining the sealing capability and stability of the UMS. The risks of the UMS failing or detaching were analyzed by changing the characteristics of the equivalent stress, gap distance, contact pressure, and strain energy density acting on the UMS during axial and radial compressions. It was advantageous that the smaller the TR, the smaller the stress distribution, but the occurrence of a detachment region was a disadvantage. A TR value of 1.0 or higher should be applied because the detachment region disappears in that case. Type 1 with open grooves showed the lowest stress distribution and the smallest detachment region. Furthermore, symmetric open grooves showed more advantageous results in terms of stress distribution and detachment than did asymmetric open grooves. For the contact pressure, type 3 with no open groove showed the highest value. However, one disadvantage of type 3 was that the stress distribution increased excessively, even causing a deformation in the insulating spacer. As for the strain energy density, type 1 with open grooves showed the most stable values of all cases. In conclusion, based on the analysis results of this study, type 1 with open grooves showed the lowest equivalent stress distribution, the smallest detachment region, and the most stable contact pressure and strain energy density, which implies the lowest risk of failure for the UMS system. The results of this study may be an important input for designing elastomeric UMS-based insulating joints, and could improve the reliability of the sealing system.