Effect of Polishing-Induced Subsurface Impurity Defects on Laser Damage Resistance of Fused Silica Optics and Their Removal with HF Acid Etching
Abstract
:1. Introduction
2. Theory and Methods
2.1. Modeling of Impurity-Induced Temperature and Thermal Distributions
2.2. Sample Preparation, SSD Removal, and Etching Process Characterization
2.3. Laser Damage Test
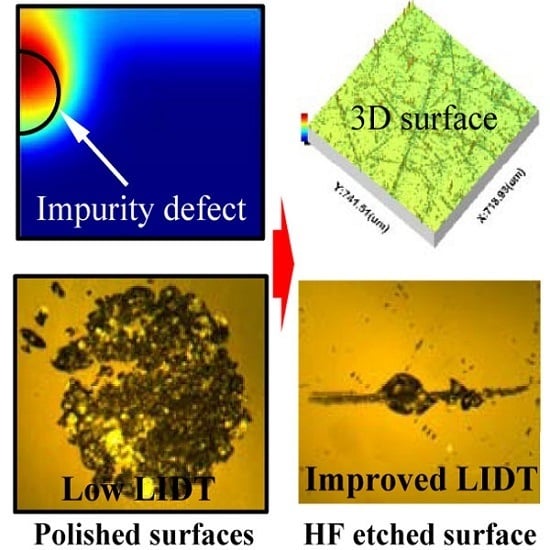
3. Results and Discussion
3.1. Temperature Distribution Caused by the Subsurface Impurity Defects
3.1.1. Comparison of Temperature Distributions with and without Impurity Defects
3.1.2. Effect of Impurity Defect Parameters on Temperature Distribution
3.2. Thermal Stress Distribution Caused by the Subsurface Impurity Defects
3.2.1. Comparison of Thermal Stress Distributions with and without Impurity Defect
3.2.2. Effect of Impurity Defect Parameters on Its Induced Thermal Stress
3.3. Removal of Subsurface Impurity Defects by HF Acid Etching
3.3.1. Etching Rate of Fused Silica
3.3.2. Surface Quality and Impurity Content of Fused Silica Etched by HF Acid
3.3.3. Laser Damage Resistance of Etched Fused Silica Surface
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stolz, C.J. The National Ignition Facility: The path to a carbon-free energy future. Philos. Trans. R. Soc. A 2012, 370, 4115–4129. [Google Scholar] [CrossRef] [PubMed]
- Hurricane, O.A.; Callahan, D.A.; Casey, D.T.; Celliers, P.M.; Cerjan, C.; Dewald, E.L.; Dittrich, T.R.; Döppner, T.; Hinkel, D.E.; Berzak Hopkins, L.F.; et al. Fuel gain exceeding unity in an inertially confined fusion implosion. Nature 2014, 506, 343–348. [Google Scholar] [CrossRef] [PubMed]
- Casner, A.; Caillaud, T.; Darbon, S.; Duval, A.; Thfouin, I.; Jadaud, J.P.; LeBreton, J.P.; Reverdin, C.; Rosse, B.; Rosch, R.; et al. LMJ/PETAL laser facility: Overview and opportunities for laboratory astrophysics. High Energy Density Phys. 2015, 17, 2–11. [Google Scholar] [CrossRef]
- Dunne, M. A high-power laser fusion facility for Europe. Nat. Phys. 2006, 2, 2–5. [Google Scholar] [CrossRef]
- Zheng, W.; Wei, X.; Zhu, Q.; Jing, F.; Hu, D.; Su, J.; Zheng, K.; Yuan, X.; Zhou, H.; Dai, W.; et al. Laser performance of the SG-III laser facility. High Power Laser Sci. Eng. 2016, 4, e21. [Google Scholar] [CrossRef]
- Campbell, J.H.; Hawley-Fedder, R.A.; Stolz, C.J.; Menapace, J.A.; Borden, M.R.; Whitman, P.K.; Yu, J.; Runkel, M.; Riley, M.O.; Feit, M.D.; et al. NIF optical materials and fabrication technologies: An overview. Proc. SPIE 2004, 5341, 84–101. [Google Scholar]
- Baisden, P.A.; Atherton, L.J.; Hawley, R.A.; Land, T.A.; Menapace, J.A.; Miller, P.E.; Runkel, M.J.; Spaeth, M.L.; Stolz, C.J.; Suratwala, T.I.; et al. Large optics for the National Ignition Facility. Fusion Sci. Technol. 2016, 69, 295–351. [Google Scholar] [CrossRef]
- Lamaignère, L.; Bercegol, H.; Bouchut, P.; During, A.; Néauport, J.; Piombini, H.; Razé, G. Enhanced optical damage resistance of fused silica surfaces using UV laser conditioning and CO2 laser treatment. Proc. SPIE 2004, 5448, 952–960. [Google Scholar]
- Raman, R.N.; Matthews, M.J.; Adams, J.J.; Demos, S.G. Monitoring annealing via CO2 laser heating of defect populations on fused silica surfaces using photoluminescence microscopy. Opt. Express 2010, 18, 15207–15215. [Google Scholar] [CrossRef] [PubMed]
- Raman, R.N.; Negres, R.A.; Matthews, M.J.; Carr, C.W. Effect of thermal anneal on growth behavior of laser-induced damage sites on the exit surface of fused silica. Opt. Mater. Express 2013, 3, 765–776. [Google Scholar] [CrossRef]
- Smith, A.V.; Do, B.T. Picosecond-nanosecond bulk damage of fused silica at 1064 nm. Proc. SPIE 2008, 7132, 71321E. [Google Scholar]
- Stäblein, J.; Pöhl, K.; Weisleder, A.; Gönna, G.; Töpfer, T.; Hein, J.; Siebold, M. Optical properties of CaF2 and Yb3+: CaF2 for laser applications. Proc. SPIE 2011, 8080, 808002. [Google Scholar]
- Azumi, M.; Nakahata, E. Study of relation between crystal structure and laser damage of Calcium Fluoride. Proc. SPIE 2010, 7842, 78421U. [Google Scholar]
- Singh, N.B.; Suhre, D.R.; Balakrishna, V.; Marable, M.; Meyer, R. Far-infrared conversion materials: Gallium Selenide for far-infrared conversion application. Prog. Cryst. Growth Charact. Mater. 1998, 37, 47–102. [Google Scholar] [CrossRef]
- DeYoreo, J.J.; Burnham, A.K.; Whitman, P.K. Developing KH2PO4 and KD2PO4 crystals for the world’s most powerful laser. Int. Mater. Rev. 2002, 47, 113–152. [Google Scholar] [CrossRef]
- Negres, R.A.; Zaitseva, N.P.; DeMange, P.; Demos, S.G. Expedited laser damage profiling of KDxH2−xPO4 with respect to crystal growth parameters. Opt. Lett. 2006, 31, 3110–3112. [Google Scholar] [CrossRef] [PubMed]
- Neauport, J.; Lamaignere, L.; Bercegol, H.; Pilon, F.; Birolleau, J.C. Polishing-induced contamination of fused silica optics and laser induced damage density at 351 nm. Opt. Express 2005, 13, 10163–10171. [Google Scholar] [CrossRef] [PubMed]
- Papernov, S.; Schmid, A.W. Laser-induced surface damage of optical materials: Absorption sources, initiation, growth, and mitigation. Proc. SPIE 2008, 7132, 71321J. [Google Scholar]
- Wang, J.; Li, Y.; Han, J.; Xu, Q.; Guo, Y. Evaluating subsurface damage in optical glasses. J. Eur. Opt. Soc. Rapid Publ. 2011, 6, 11001. [Google Scholar]
- Camp, D.W.; Kozlowski, M.R.; Sheehan, L.M.; Nichols, M.; Dovik, M.; Raether, R.; Thomas, I. Subsurface damage and polishing compound affect the 355-nm laser damage threshold of fused silica surfaces. Proc. SPIE 1998, 3244, 356–364. [Google Scholar]
- Feit, M.D.; Rubenchik, A.M. Influence of subsurface cracks on laser induced surface damage. Proc. SPIE 2004, 5273, 264–272. [Google Scholar]
- Neauport, J.; Cormont, P.; Legros, P.; Ambard, C.; Destribats, J. Imaging subsurface damage of grinded fused silica optics by confocal fluorescence microscopy. Opt. Express 2009, 17, 3543–3554. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Huang, J.; Wang, F.; Zhou, X.; Jiang, X.; Dong, W.; Zheng, W. Photoluminescence defects on subsurface layer of fused silica and its effects on laser damage performance. Proc. SPIE 2015, 9255, 92553V. [Google Scholar]
- Hu, G.; Zhao, Y.; Liu, X.; Li, D.; Xiao, Q.; Yi, K.; Shao, J. Combining wet etching and real-time damage event imaging to reveal the most dangerous laser damage initiator in fused silica. Opt. Lett. 2013, 38, 2632–2635. [Google Scholar] [CrossRef] [PubMed]
- Neauport, J.; Cormont, P.; Lamaignère, L.; Ambard, C.; Pilon, F.; Bercegol, H. Concerning the impact of polishing induced contamination of fused silica optics on the laser-induced damage density at 351 nm. Opt. Commun. 2008, 281, 3802–3805. [Google Scholar] [CrossRef]
- Suratwala, T.I.; Miller, P.E.; Bude, J.D.; Steele, W.A.; Shen, N.; Monticelli, M.V.; Feit, M.D.; Laurence, T.A.; Norton, M.A.; Carr, C.W.; et al. HF-based etching processes for improving laser damage resistance of fused silica optical surfaces. J. Am. Ceram. Soc. 2011, 94, 416–428. [Google Scholar] [CrossRef]
- Ye, H.; Li, Y.; Yuan, Z.; Wang, J.; Yang, W.; Xu, Q. Laser induced damage characteristics of fused silica optics treated by wet chemical processes. Appl. Surf. Sci. 2015, 357, 498–505. [Google Scholar] [CrossRef]
- Ye, H.; Li, Y.; Zhang, Q.; Wang, W.; Yuan, Z.; Wang, J.; Xu, Q. Post-processing of fused silica and its effects on damage resistance to nanosecond pulsed UV lasers. Appl. Opt. 2016, 55, 3017–3025. [Google Scholar] [CrossRef] [PubMed]
- Stevens-Kalceff, M.A.; Wong, J. Distribution of defects induced in fused silica by ultraviolet laser pulses before and after treatment with a CO2 laser. J. Appl. Phys. 2005, 97, 113519. [Google Scholar] [CrossRef]
- Hrubesh, L.W.; Norton, M.A.; Molander, W.A.; Donohue, E.E.; Maricle, S.M.; Penetrante, B.M.; Brusasco, R.M.; Grundler, W.; Butler, J.A.; Carr, J.W.; et al. Methods for mitigating surface damage growth on NIF final optics. Proc. SPIE 2002, 4679, 23–33. [Google Scholar]
- Menapace, J.A.; Davis, P.J.; Steele, W.A.; Wong, L.L.; Suratwala, T.I.; Miller, P.E. MRF applications: Measurement of process-dependent subsurface damage in optical materials using the MRF wedge technique. Proc. SPIE 2006, 5991, 599103. [Google Scholar]
- Cormont, P.; Gallais, L.; Lamaignère, L.; Donval, T.; Rullier, J.L. Effect of CO2 laser annealing on residual stress and on laser damage resistance for fused silica optics. Proc. SPIE 2010, 7842, 78422C. [Google Scholar]
- Jiang, X.; Liu, Y.; Rao, H.; Fu, S. Improve the laser damage resistance of fused silica by wet surface cleaning and optimized HF etch process. Proc. SPIE 2013, 8786, 87860Q. [Google Scholar]
- Gao, X.; Feng, G.; Han, J.; Zhai, L. Investigation of laser-induced damage by various initiators on the subsurface of fused silica. Opt. Express 2012, 20, 22095–22101. [Google Scholar] [CrossRef] [PubMed]
- Moncayo, M.A.; Santhanakrishnan, S.; Vora, H.D.; Dahotre, N.B. Computational modeling and experimental based parametric study of multi-track laser processing on alumina. Opt. Laser Technol. 2013, 48, 570–579. [Google Scholar] [CrossRef]
- Wang, X.; Shen, Z.H.; Lu, J.; Ni, X.W. Laser-induced damage threshold of silicon in millisecond, nanosecond, and picosecond regimes. J. Appl. Phys. 2010, 108, 033103. [Google Scholar]
- Samant, A.N.; Dahotre, N.B. Laser machining of structural ceramics—A review. J. Eur. Ceram. Soc. 2009, 29, 969–993. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill Book Company: New York, NY, USA, 1970; pp. 1248–1297. 1297. [Google Scholar]
- Lide, D.R. Handbook of Chemistry and Physics, 84th ed.; CRC Press: Boca Raton, FL, USA, 2003; pp. 27–80. [Google Scholar]
- Martienssen, W.; Warlimont, H. Handbook of Condensed Matter and Materials Data, 1st ed.; Springer: New York, NY, USA, 2005; pp. 161–407, 523–559. [Google Scholar]
- Walker, P.; Tarn, W.H. Handbook of Metal Etchants, 1st ed.; CRC Press: Boca Raton, FL, USA, 1991; pp. 76–106, 719–738. [Google Scholar]
- Sato, K.; Yugami, H.; Hashida, T. Effect of rare-earth oxides on fracture properties of ceria ceramics. J. Mater. Sci. 2004, 39, 5765–5770. [Google Scholar] [CrossRef]
- Miller, P.E.; Suratwala, T.I.; Wong, L.L.; Feit, M.D.; Menapace, J.A.; Davisand, P.J.; Steele, R.A. The Distribution of Subsurface Damage in Fused Silica. Proc. SPIE 2005, 5991, 599101. [Google Scholar]
- Cheng, J.; Chen, M.; Liao, W.; Wang, H.; Xiao, Y.; Li, M. Fabrication of spherical mitigation pit on KH2PO4 crystal by micro-milling and modeling of its induced light intensification. Opt. Express 2013, 21, 16799–16813. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Zhao, Y.; Li, D.; Xiao, Q.; Shao, J.; Fan, Z. Studies of laser damage morphology reveal subsurface feature in fused silica. Surf. Interface Anal. 2010, 42, 1465–1468. [Google Scholar] [CrossRef]














| Property | Nomenclature | Value (Units) |
|---|---|---|
| Molar mass | M | 60.06 (g/mol) |
| Crystal system | – | Amorphous |
| Density | ρ | 2.21 (g/cm3) |
| Melting point | Tm | 1900 (°C) |
| Thermo-optical coefficient | ε | 1 × 10−5 |
| Coefficient of linear expansion | αt | 5.5 × 10−7 °C−1 |
| Specific heat capacity | c | 0.728 J/(g·°C) |
| Heat conductivity coefficient | k | 1.35 W/(m·°C) |
| Relative dielectric constant | εr | 2.25 |
| Young modulus | E | 7.36 × 1010 (Pa) |
| Shear modulus | G | 3.14 × 1010 (Pa) |
| Compressive strength | P | 800~1000 (MPa) |
| Poisson’s ratio | ν | 0.17 |
| Defect Species | Density (g/cm3) | Specific Heat Capacity (J/(g·°C)) | Heat Conductivity (W/(cm·°C)) | Coefficient of Linear Expansion (×10−6 K−1) | Young Modulus (GPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| Fe | 7.0 | 0.45 | 0.565 | 11.8 | 152.0 | 0.30 |
| Al | 2.7 | 0.88 | 2.38 | 23.0 | 70.0 | 0.33 |
| CeO2 | 7.13 | 0.465 | 0.045 | 13.2 | 174 | 0.32 |
| Pulse Width τp/ns | Wavelength λ/nm | Repetition Rate ν/Hz | Beam Diameter D/μm | Incident Angle θi/deg | Laser Modal | Divergence Angle θd/mrad |
|---|---|---|---|---|---|---|
| 10 | 355 | 1 | 390 | 0 | TEM00 | ≤2.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Wang, J.; Hou, J.; Wang, H.; Zhang, L. Effect of Polishing-Induced Subsurface Impurity Defects on Laser Damage Resistance of Fused Silica Optics and Their Removal with HF Acid Etching. Appl. Sci. 2017, 7, 838. https://doi.org/10.3390/app7080838
Cheng J, Wang J, Hou J, Wang H, Zhang L. Effect of Polishing-Induced Subsurface Impurity Defects on Laser Damage Resistance of Fused Silica Optics and Their Removal with HF Acid Etching. Applied Sciences. 2017; 7(8):838. https://doi.org/10.3390/app7080838
Chicago/Turabian StyleCheng, Jian, Jinghe Wang, Jing Hou, Hongxiang Wang, and Lei Zhang. 2017. "Effect of Polishing-Induced Subsurface Impurity Defects on Laser Damage Resistance of Fused Silica Optics and Their Removal with HF Acid Etching" Applied Sciences 7, no. 8: 838. https://doi.org/10.3390/app7080838
APA StyleCheng, J., Wang, J., Hou, J., Wang, H., & Zhang, L. (2017). Effect of Polishing-Induced Subsurface Impurity Defects on Laser Damage Resistance of Fused Silica Optics and Their Removal with HF Acid Etching. Applied Sciences, 7(8), 838. https://doi.org/10.3390/app7080838