Forced Response Prediction of Turbine Blades with Flexible Dampers: The Impact of Engineering Modelling Choices
Abstract
:1. Introduction
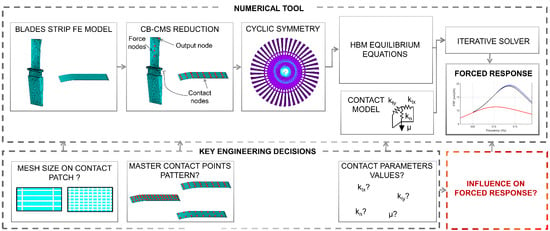
- The strip damper is modelled using finite elements given its high flexibility. Does the mesh discretization, especially around the contact area, significantly affect results?
- A subset of nodes is selected on the strip damper contact area and contact elements are applied to take into account the presence of friction. A uniform distribution of contact elements seems to be the most logical choice, but does the selected pattern (and number of contact elements) affect the position of the resonant frequencies?
- Each contact element requires calibration parameters (e.g., contact stiffness). Under which conditions do these elements most significantly affect results?
2. Numerical Model
- M, C, and K are the mass, damping stiffness matrices of the system respectively. They are obtained by combining the mass, damping and stiffness matrices of both strip and blades. Usually these matrices are extracted from the FE models of strip and blades after a Craig Bampton-Component Mode Synthesis (CB-CMS) reduction;
- is the vector of the DOFs of strip and blades. Due to the CB-CMS reduction, this vector includes both modal DOFs and the physical DOFs which are the displacements of the master nodes retained in the reduction.
- is the vector of external forces acting on the system, i.e., the sum of the external excitation vector , acting on the blade airfoil, and the centrifugal force vector , pushing the strip against the blade platform as shown in Figure 1.
- is the vector of friction nonlinear forces generated between the blade-strip coupled nodes by their relative displacements. Equation (1) is nonlinear due to the presence of that depends on the relative displacement between strip and blades.
- is the fundamental frequency of the excitation force.
- is the number of harmonics that approximate the functions. More the harmonics, better the approximation, but larger the computational time.
- The subscript n refers to the harmonic Fourier coefficient.
- ℜ indicates the real part of forces and displacements.
- The centrifugal forces , acting on the strip nodes, are static forces and therefore they appear only in the zero-order harmonic .
- The external excitations are approximated from the first harmonic onwards as , for .
- is the dynamic stiffness matrix of the system, corresponding to the harmonic. The 0th order represents the static balance equation, where only the centrifugal forces are considered.
- The vectors , and represent the Fourier coefficients of the harmonic.
2.1. Contact Model
2.2. Numerical Calculation
3. Influence of Key Parameters on the Response
- (1)
- The mesh size in the FE model of the contact areas.
- (2)
- The number of master contact nodes retained in the CB-CMS reduction.
- (3)
- The contact parameters values in the contact model (contact stiffness values as described above).
3.1. Definition of the Nominal Parameter Values and of the Benchmark Case
3.2. FE Model: Influence of Mesh Size in the Contact Area
3.3. Craig-Bampton Reduction: Influence of the Retained Contact Nodes
- If a sufficiently high contact nodes density is adopted (i.e., 4.5 node columns per cm and 7 node rows per cm respectively) the predicted frequency reaches an asymptotic value.
- If the number of node rows decreases below its threshold value, the frequency starts increasing.
- If the number of node columns decreases below its threshold value, the frequency starts decreasing.
3.3.1. Density of Nodes Incremented Along the Strip Long-Edge Direction X
- Does the method (or pattern) the designer uses to refine its contact node selection affect results?
- Why does the frequency decrease if the contact nodes density decreases?
3.3.2. Density of Nodes Incremented Along the Strip Short-Edge Direction Y
- as more rows of nodes are retained, the local contact stiffness values at each node are reduced (see Section 2.1);
- as a result, the rows of springs connected to the high mobility region will progressively offer a weaker constraint;
- conversely, the additional rows created far from the high mobility region do not significantly modify the stiffness of the system as the nodes they are connected to are not very mobile.
3.3.3. On the Cross-Influence between Retained Nodes Number and FE Model Mesh Refinement
3.4. On the Cross-Influence between Retained Nodes Number and Mode Shape under Investigation
3.5. Contact Model: Influence of Contact Parameters
- EO = 0 means that the blades vibrate with the same phase, that is In-Phase (IP).
- EO = 22 (that is the number of the blades 44 divided by two) means that the blades vibrate with opposite phase, that is Out-of-Phase (OOP).
3.6. On the Cross-Influence between Retained Nodes Number and the Contact Stiffness Values
4. Engineering Choices: Guidelines for the Designer
- There are no particular requirements for the blade and strip FE models. “Standard” accuracy levels (typical of industrial FE models, i.e., mesh grid size on contact patch ≈ 1 mm) are quite sufficient. The mesh size does not have a significant influence on the results in terms of dynamic response. This low sensitivity is easily explained, since the additional compliance offered by a very fine mesh is still orders of magnitude higher than expected values of stiffness at the contact. This is especially true in the case of flexible dampers, as the centrifugal force is limited and, as a result, expected contact stiffness values are moderate [38]. The authors advise designers to adopt, as a good practice, a regular mesh both on the blade and on the strip contact patches. This choice will ensure an easy selection of the contact nodes to be retained in the CB-CMS condensation procedure.
- If the mode of interest is a bending mode where the platform of the blade is moving during vibration, the number and location of contact master nodes retained in the CB reduction has critical effects on the numerical prediction. Ensuring a fine discretization of the contact patch is paramount to mimicking the real contact conditions (conforming surfaces and uniform centrifugal pressure application). The asymptotic behavior evidenced in Figure 6b suggests that a convergence study in the linear regime can easily identify the number of contact nodes which will ensure a trustworthy representation of the contact patch at the minimum computational cost. In the present case, the application of 4.5 node columns per cm (in the X strip longest edge direction) and 7 node rows per cm (in the Y strip shortest edge direction) ensured predicted frequency values which did not change even if the contact node density increased further.
- Assigning each contact node an equal fraction of the global contact stiffness is a standard practice, typically adopted for rigid dampers. This investigation shows that this uniform division does not ensure an equal equivalent stiffness (i.e., equal stick resonance frequency) if the number of contact nodes varies. This is due to the fact that the contact patch is characterized by a nonuniform kinematics (caused by the damper flexibility). As a result, a portion of the contact patch (in the present case aligned along the strip longest edge), here termed high mobility region, will display a higher relative blade-strip displacement. The “local” value of the contact springs of the nodes belonging to the high mobility region will strongly influence the response prediction, while the values assigned to nodes located elsewhere will have negligible effect. Locating the shape and position of the high mobility region becomes relevant if the designer is forced to reduce the number of contact nodes (e.g., in the nonlinear calculation) to limit the required computational capabilities. Having knowledge of the shape and position of the high mobility region will enable the designer to reduce the number of contact points in such a way as to provide a conservative estimate of the frequency shift, rather than an overestimation.
- The contact stiffness values need to be determined through a direct experimental investigation. They could be derived from an ad-hoc campaign on a tribology experimental test rig or by tuning contact stiffness values to obtain experimental natural frequency in stick condition for different EO excitations. If the second option was to be preferred, the low sensitivity of the response to variations of values during IP vibration and the low sensitivity to variations in case of OOP vibration evidenced in Section 3.5 could be exploited. This set of observations, involving experiments at different EO excitations, could help identify a unique set of contact parameters and thus overcome the multiplicity of solutions identified in Section 3.6. This second option has another important advantage: it automatically takes into account the flexibility of the mesh at the contact (albeit in this paper negligible, with respect to other parameters). In this way, the contact stiffness values and will be defined as the additional stiffness contribution (e.g., due to local asperities) that the standard FE mesh is unable to model.
5. Conclusions
- introduction of the FE model of the strip damper (rigid/solid dampers are modeled using a rigid body assumption);
- contact parameters determined for lower values of contact pressure are used (strip dampers, given their limited mass generate a moderate centrifugal force).
- Mesh size, provided it meets a minimum quality standard, does not critically influence the response.
- The flexibility of the strip generates complex kinematics at the contact. In detail, portions of the contact patch display higher relative displacements. As a result, only a high density of contact points will ensure an adequate representation of the contact conditions. The minimum density which ensures an adequate representation of the contact patch can be found through a convergence study in the low excitation (i.e., linear regime).
- Contact stiffness values can strongly influence the response, depending on the relative displacement at the contact (i.e., produced by different EO excitation). In detail, the influence will be at its maximum if the contact spring is parallel to the blade-strip relative displacement, while contact springs whose direction is orthogonal to the relative blade-strip relative displacement will have a negligible effect on the predicted response.
- Multiple combinations of contact parameters can lead to the same predicted response (i.e., multiple solutions to the contact parameter problem).
Author Contributions
Conflicts of Interest
Abbreviations
| CB-CMS | Craig Bampton-Component Mode Synthesis |
| DOF(s) | Degree(s) Of Freedom |
| EO | Engine Order |
| FE | Finite Elements |
| FRF | Frequency Response Function |
| MHBM | Multi-Harmonic Balance Method |
| Mesh Multiplying Factor | |
| Stiffness Multiplying Factor |
References
- Griffin, J.H. Friction Damping of Resonant Stresses in Gas Turbine Airfoils. J. Eng. Power 1980, 102, 329–333. [Google Scholar] [CrossRef]
- Aeromechanics Design of Turbine Blades (ADturB). Result in Brief: High Cycle Fatigue under High Profile Study; Techreport, Project ID: BRPR950124; European Union: City of Brussels, Belgium, 2000.
- Szwedowicz, J. Bladed disks: Non linear dynamics. In Structural Design of Aircraft Engines: Key Objectives and Techniques; Seinturier, E., Paniagua, G., Eds.; von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 2008. [Google Scholar]
- Petrov, E.P. Explicit Finite Element Models of Friction Dampers in Forced Response Analysis of Bladed Disks. J. Eng. Gas Turbines Power 2008, 130, 022502. [Google Scholar] [CrossRef]
- Yang, B.D.; Chen, J.J.; Menq, C.H. Prediction of resonant response of shrouded blades with three-dimensional shroud constraint. J. Eng. Gas Turbines Power 1999, 121, 523–529. [Google Scholar] [CrossRef]
- Shi, Y.; Hong, J.; Shan, Y.; Zhu, Z. Forced response analysis of shrouded blades by an alternating frequency/time domain method. In Proceedings of the ASME Turbo Expo: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006. [Google Scholar] [CrossRef]
- Szwedowicz, J.; Visser, R.; Sextro, W.; Masserey, P.A. On Nonlinear Forced Vibration of Shrouded Turbine Blades. J. Turbomach. 2007, 130, 011002. [Google Scholar] [CrossRef]
- Gu, W.; Xu, Z.; Liu, Y. A method to predict the nonlinear vibratory response of bladed disc system with shrouded dampers. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 226, 1620–1632. [Google Scholar] [CrossRef]
- Berruti, T.; Maschio, V. Experimental Investigation on the Forced Response of a Dummy Counter-Rotating Turbine Stage With Friction Damping. J. Eng. Gas Turbines Power 2012, 134, 1–8. [Google Scholar] [CrossRef]
- Yanq, B.D.; Menq, C.H. Characterization of contact kinematics and application to the design of wedge dampers in turbomachinery application: Part2—Prediction of forced response and experimental verification. J. Eng. Gas Turbines Power 1998, 120, 418–423. [Google Scholar] [CrossRef]
- Panning, L.; Sextro, W.; Popp, K. Optimization of interblade friction damper design. In Proceedings of the ASME Turbo Expo 2000: Power for Land, Sea, and Air, Munich, Germany, 8–11 May 2000. [Google Scholar]
- Panning, L.; Sextro, W.; Popp, K. Spatial dynamics of tuned and mistuned bladed disks with cylindrical and wedge-shaped friction dampers. J. Rotat. Mach. 2003, 9, 219–228. [Google Scholar] [CrossRef]
- Petrov, E.P.; Ewins, D.J. Advanced modeling of underplatform friction dampers for analysis of bladed disk vibration. J. Turbomach. 2007, 129, 143–150. [Google Scholar] [CrossRef]
- Berruti, T.; Firrone, C.M.; Pizzolante, M.; Gola, M.M. Fatigue damage prevention on turbine blades: Study of underplatform damper shape. Key Eng. Mater. 2007, 347, 159–164. [Google Scholar] [CrossRef]
- Sever, I.A.; Petrov, E.P.; Ewins, D.J. Experimental and Numerical Investigation of Rotating Bladed Disk Forced Response Using Underplatform Friction Dampers. J. Eng. Gas Turbines Power 2008, 130, 042503. [Google Scholar] [CrossRef]
- Cigeroglu, E.; An, N.; Menq, C.H. Forced response prediction of constrained and unconstrained structures coupled through friction contacts. J. Eng. Gas Turbines Power 2008, 131, 1–11. [Google Scholar]
- Afzal, M.; Lopez Arteaga, I.; Kari, L. Investigation of damping potential of strip damper on a real turbine blade. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, South Korea, 13–17 June 2016. [Google Scholar]
- Sanliturk, K.Y.; Ewins, D.J.; Stanbridge, A.B. Underplatform dampers for turbine blades: Theoretical modeling, analysis and comparison with experimental data. J. Eng. Gas Turbines Power 2001, 123, 919–929. [Google Scholar] [CrossRef]
- Panning, L.; Popp, K.; Sextro, W.; Gotting, F.; Kayser, A.; Wolter, I. Asymmetrical Underplatform Dampers in Gas Turbine Bladings: Theory and Application. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004; pp. 269–280. [Google Scholar]
- Berruti, T.; Gola, M.M.; Zucca, S. Underplatform Damper Performance with Turbine Blades. In Proceedings of the NATO AVT-121 Symposium on Evaluation, Control and Prevention of High Cycle Fatigue, Granada, Spain, 3–7 October 2005. [Google Scholar]
- Zucca, S.; Borrajo, J.; Gola, M.M. Forced Response of Bladed Disks in Cyclic Symmetry with Underplatform Dampers. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea and Air, Barcelona, Spain, 8–11 May 2006. [Google Scholar]
- Koh, K.H.; Griffin, J.H. Dynamic Behavior of Spherical Friction Dampers and its Implication to Damper Contact Stifness. J. Eng. Gas Turbines Power 2007, 129, 511–521. [Google Scholar] [CrossRef]
- Firrone, C.M.; Zucca, S.; Gola, M.M. The effect of underplatform dampers on the forced response of bladed disks by a coupled static/dynamic harmonic balance method. J. Non-Linear Mech. 2011, 46, 363–375. [Google Scholar] [CrossRef]
- Berruti, T.; Firrone, C.M.; Gola, M.M. A Test Rig for Noncontact Traveling Wave Excitation of a Bladed Disk with Underplatform Dampers. J. Eng. Gas Turbines Power 2011, 133, 1–7. [Google Scholar] [CrossRef]
- Gastaldi, C.; Berruti, T.; Gola, M.M. The relevance of damper pre-optimization and its effectiveness on the forced response of blades. In Proceedings of the ASME Turbo Expo 2017: Power for Land, Sea and Air, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Cardona, A.; Coune, T.; Lerusse, A. A multi-harmonic method for nonlinear vibration analysis. J. Numer. Methods Eng. 1998, 217, 1593–1608. [Google Scholar]
- Sanliturk, K.Y.; Ewins, D.J. Modelling two-dimensional friction contact and its application using harmonic balance method. J. Sound Vib. 1996, 193, 511–523. [Google Scholar] [CrossRef]
- Siewert, C.; Panning, L.; Wallaschek, J.; Richter, C. Multiharmonic forced response analysis of a turbine blading coupled by nonlinear contact forces. J. Eng. Gas Turbines Power 2010, 132, 1–9. [Google Scholar] [CrossRef]
- Craig, R.R.; Bampton, M.C.C. Coupling of substructures for dynamic analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar]
- Petrov, E.P.; Ewins, D.J. Analytical Formulation of Friction Interface Elements for Analysis on Nonlinear Multi-Harmonic Vibrations of Bladed Disks. J. Turbomach. 2003, 125, 364–371. [Google Scholar] [CrossRef]
- Borrajo, J.M.; Zucca, S.; Gola, M.M. Analytical formulation of the Jacobian matrix for non-linear calculation of the forced response of turbine blade assemblies with wedge friction dampers. J. Non-Linear Mech. 2006, 41, 1118–1127. [Google Scholar] [CrossRef]
- Gastaldi, C.; Berruti, T.M. A method to solve the efficiency accuracy trade-off of multi-harmonic balance calculation of structures with friction contacts. J. Non-Linear Mech. 2017, 129, 25–40. [Google Scholar] [CrossRef]
- Schwingshackl, C.W.; Petrov, E.P.; Ewins, D.J. Effects of contact interface parameters on vibration of turbine bladed disks with underplatform dampers. J. Eng. Gas Turbines Power 2012, 134, 032507. [Google Scholar] [CrossRef]
- Gastaldi, C.; Gola, M.M. A random sampling stregy for tuning contact parameters of underplatform dampers. In Proceedings of the ASME Turbo Expo 2015: Power for Land, Sea and Air, Montreal, QC, Canada, 15–19 June 2015. [Google Scholar]
- Zucca, S.; Firrone, C.M.; Gola, M. Modeling underplatform dampers for turbine blades: A refined approach in the frequency domain. J. Vib. Control 2012, 19, 1087–1102. [Google Scholar] [CrossRef]
- Firrone, C.M.; Zucca, S. Modeling Friction Contacts in Structural Dynamics and its Application to Turbine Bladed Disks. Numer. Anal. Theory Appl. 2011, 14, 301–334. [Google Scholar]
- Yang, B.D.; Menq, C.H. Characterization of 3D contact kinematics and prediction of resonant response of structures having 3D frictional constraint. J. Sound Vib. 1998, 217, 909–925. [Google Scholar] [CrossRef]
- Gastaldi, C. Vibration Control and Mitigation in Turbomachinery. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2017. [Google Scholar]
- Gastaldi, C.; Gola, M. Pre-optimization of asymmetrical underplatform dampers. J. Eng. Gas Turbines Power 2016, 139, 012504. [Google Scholar] [CrossRef]
- Cameron, T.; Griffin, J. An alternating frequency/time domain method for calculating the steady-state response of nonlinear dynamic system. J. Appl. Mech. 1989, 56, 149–154. [Google Scholar] [CrossRef]
- Lavella, M. Contact properties and wear behaviour of nickel based superalloy ren 80. Metals 2016, 6, 159. [Google Scholar] [CrossRef]
- Botto, D.; Gastadi, C.; Gola, M.M.; Umer, M. An Experimental Investigation of the Dynamics of a Blade with Two Under-Platform Dampers. ASME. J. Eng. Gas Turbines Power 2017, 140, 032504-9. [Google Scholar] [CrossRef]















| Mesh Size | Number of Master Contact Nodes | Contact Parameter Values | |
|---|---|---|---|
| Nominal value | Rectangular grid , [2.5 × 1] mm elements | 715 nodes per contact patch | = 1000 N/μm k = 233 N/μm |
| Explored variation | MMF = 1, [2.5 × 1] mm elements = 0.5, [1.25 × 1] mm elements = 0.25, [0.63 × 1] mm elements | 2 to 715 nodes per contact patch | 0.5 for for |
| Patterns | Number of Node Columns (Corresponding Node Density [nodes/cm]) | |||||
|---|---|---|---|---|---|---|
| A | 3 (0.3) | 5 (0.5) | 9 (0.9) | 17 (1.7) | 33 (3.3) | 65 (6.5) |
| B | 4 (0.4) | 7 (0.7) | 13 (1.3) | 25 (2.5) | 49 (4.9) | - |
| C | 6 (0.6) | 11 (1.1) | 21 (2.1) | 41 (4.1) | - | - |
| D | 8 (0.8) | 15 (1.5) | 29 (2.9) | 57 (5.7) | - | - |
| E | 10 (1.0) | 19 (1.9) | 37 (3.7) | 73 (7.3) | - | - |
| Key parameters | Guidelines |
|---|---|
| Mesh size | Regular mesh on the blade and strip contact surfaces, grid size approximately 1 mm. |
| Master contact nodes density | 4.5 nodes/cm along the contact long edge, 7 nodes/cm along the contact short edge. A convergence study in linear regime (springs between contact nodes), see Figure 6b, is suggested to ensure an accurate choice if different modes (e.g., torsional) are investigated. |
| Contact stiffness values | To be determined experimentally. In the present case = 1000 N/μm and = 233 N/μm were assumed from experiments performed on rigid dampers having the same geometry, material and contact pressure as the strip object of this investigation. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gastaldi, C.; Fantetti, A.; Berruti, T.M. Forced Response Prediction of Turbine Blades with Flexible Dampers: The Impact of Engineering Modelling Choices. Appl. Sci. 2018, 8, 34. https://doi.org/10.3390/app8010034
Gastaldi C, Fantetti A, Berruti TM. Forced Response Prediction of Turbine Blades with Flexible Dampers: The Impact of Engineering Modelling Choices. Applied Sciences. 2018; 8(1):34. https://doi.org/10.3390/app8010034
Chicago/Turabian StyleGastaldi, Chiara, Alfredo Fantetti, and Teresa M. Berruti. 2018. "Forced Response Prediction of Turbine Blades with Flexible Dampers: The Impact of Engineering Modelling Choices" Applied Sciences 8, no. 1: 34. https://doi.org/10.3390/app8010034
APA StyleGastaldi, C., Fantetti, A., & Berruti, T. M. (2018). Forced Response Prediction of Turbine Blades with Flexible Dampers: The Impact of Engineering Modelling Choices. Applied Sciences, 8(1), 34. https://doi.org/10.3390/app8010034