Improving Roadside Unit Deployment in Vehicular Networks by Exploiting Genetic Algorithms
Abstract
:1. Introduction
2. Related Work
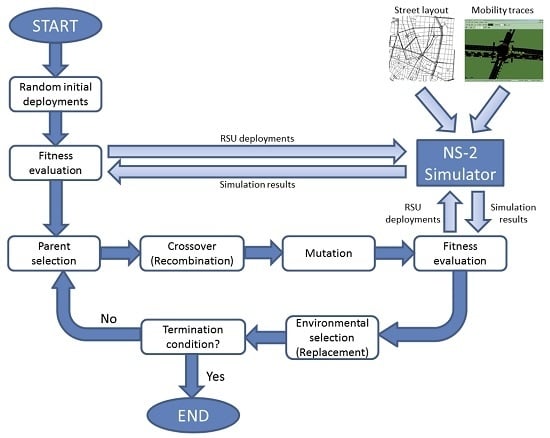
3. GARSUD: Automatic RSU Deployment
3.1. Representation of Individuals
3.2. Parent Selection
3.3. Crossover or Re-Combination
3.4. Mutation
3.5. Replacement
3.6. Fitness Function
4. Simulation Environment
5. Simulation Results
5.1. Performance of the Genetic Algorithm Used by GARSUD
5.2. Performance Comparison between GARSUD and Other Existing Approaches
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marquez-Barja, J.M.; Ahmadi, H.; Tornell, S.M.; Calafate, C.T.; Cano, J.C.; Manzoni, P.; DaSilva, L.A. Breaking the Vehicular Wireless Communications Barriers: Vertical Handover Techniques for Heterogeneous Networks. IEEE Trans. Veh. Technol. 2015, 64, 5878–5890. [Google Scholar] [CrossRef]
- Marquez-Barja, J.; Calafate, C.T.; Cano, J.C.; Manzoni, P. Performance trade-offs of a IEEE 802.21-based vertical handover decision algorithm under different network conditions. In Proceedings of the 10th IEEE International Symposium on Network Computing and Applications (NCA11), Cambridge, MA, USA, 25–27 August 2011; pp. 294–297. [Google Scholar]
- Tao, J.; Zhu, L.; Wang, X.; He, J.; Liu, Y. RSU deployment scheme with power control for highway message propagation in VANETs. In Proceedings of the IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 169–174. [Google Scholar]
- Barrachina, J.; Garrido, P.; Fogue, M.; Martinez, F.; Cano, J.; Calafate, C.; Manzoni, P. Road Side Unit Deployment: A Density-Based Approach. IEEE Intell. Transp. Syst. Mag. 2013, 5, 30–39. [Google Scholar] [CrossRef]
- Król, D.; Lasota, T.; Trawinski, B.; Trawinski, K. Investigation of evolutionary optimization methods of TSK fuzzy model for real estate appraisal. Int. J. Hybrid Intell. Syst. 2008, 5, 111–128. [Google Scholar] [CrossRef]
- Dzeng, R.J.; Lee, H.Y. Optimizing the development schedule of resort projects by integrating simulation and genetic algorithm. Int. J. Proj. Manag. 2007, 25, 506–516. [Google Scholar] [CrossRef]
- Morano, P.; Tajani, F.; Locurcio, M. GIS application and econometric analysis for the verification of the financial feasibility of roof-top wind turbines in the city of Bari (Italy). Renew. Sustain. Energy Rev. 2017, 70, 999–1010. [Google Scholar]
- Makkawi, A.; Daher, R.; Rizk, R. RSUs placement using cumulative weight based method for urban and rural roads. In Proceedings of the 7th International Workshop on Reliable Networks Design and Modeling (RNDM), Munich, Germany, 5–7 October 2015; pp. 307–313. [Google Scholar]
- Liu, Y.; Ma, J.; Niu, J.; Zhang, Y.; Wang, W. Roadside units deployment for content downloading in vehicular networks. In Proceedings of the IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 6365–6370. [Google Scholar]
- Cumbal, R.; Palacios, H.; Hincapie, R. Optimum deployment of RSU for efficient communications multi-hop from vehicle to infrastructure on VANET. In Proceedings of the IEEE Colombian Conference on Communications and Computing (COLCOM), Cartagena, Colombia, 27–29 April 2016; pp. 1–6. [Google Scholar]
- Trullols, O.; Fiore, M.; Casetti, C.; Chiasserini, C.; Ordinas, J.B. Planning roadside infrastructure for information dissemination in intelligent transportation systems. Comput. Commun. 2010, 33, 432–442. [Google Scholar] [CrossRef]
- Cavalcante, E.S.; Aquino, A.L.; Pappa, G.L.; Loureiro, A.A. Roadside Unit Deployment for Information Dissemination in a VANET: An Evolutionary Approach. In Proceedings of the 14th Annual Conference Companion on Genetic and Evolutionary Computation, GECCO ’12, Philadelphia, PA, USA, 7–11 July 2012; ACM: New York, NY, USA, 2012; pp. 27–34. [Google Scholar]
- Kim, D.; Velasco, Y.; Wang, W.; Uma, R.; Hussain, R.; Lee, S. A New Comprehensive RSU Installation Strategy for Cost-Efficient VANET Deployment. IEEE Trans. Veh. Technol. 2017, 66, 4200–4211. [Google Scholar] [CrossRef]
- Jo, Y.; Jeong, J. RPA: Road-Side Units Placement Algorithm for Multihop Data Delivery in Vehicular Networks. In Proceedings of the 30th International Conference on Advanced Information Networking and Applications Workshops (WAINA), Crans-Montana, Switzerland, 23–25 March 2016; pp. 262–266. [Google Scholar]
- Song, Y.; Lin, B.; Tian, Y.; Ding, N.; He, R.; Zhao, T. Heterogeneous Roadside Unit Placement in Eco-Sustainable Communication Networks for Intelligent Transportation. In Proceedings of the Ninth International Conference on Frontier of Computer Science and Technology, Dalian, China, 26–28 August 2015; pp. 214–219. [Google Scholar]
- Zhang, B.; Zhu, G.; Xu, S.; Zhang, N. Energy-efficient roadside units deployment in Vehicular Ad hoc Networks. In Proceedings of the 6th International Conference on Wireless, Mobile and Multi-Media (ICWMMN 2015), Beijing, China, 20–23 November 2015; pp. 6–10. [Google Scholar]
- Liang, Y.; Liu, H.; Rajan, D. Optimal Placement and Configuration of Roadside Units in Vehicular Networks. In Proceedings of the 2012 IEEE 75th Vehicular Technology Conference (VTC Spring), Yokohama, Japan, 6–9 May 2012; pp. 1–6. [Google Scholar]
- Wang, Y.; Zheng, J.; Mitton, N. Delivery Delay Analysis for Roadside Unit Deployment in Vehicular Ad Hoc Networks With Intermittent Connectivity. IEEE Trans. Veh. Technol. 2016, 65, 8591–8602. [Google Scholar] [CrossRef]
- Filippini, I.; Malandrino, F.; Dán, G.; Cesana, M.; Casetti, C.; Marsh, I. Non-cooperative RSU deployment in vehicular networks. In Proceedings of the 2012 9th Annual Conference on Wireless On-demand Network Systems and Services (WONS), Courmayeur, Italy, 9–11 January 2012; pp. 79–82. [Google Scholar]
- Massobrio, R.; Bertinat, S.; Nesmachnow, S.; Toutouh, J.; Alba, E. Smart placement of RSU for vehicular networks using multiobjective evolutionary algorithms. In Proceedings of the Latin America Congress on Computational Intelligence (LA-CCI), Curitiba, Brazil, 13–16 October 2015; pp. 1–6. [Google Scholar]
- Kibilda, J.; Galkin, B.; DaSilva, L.A. Modelling Multi-Operator Base Station Deployment Patterns in Cellular Networks. IEEE Trans. Mob. Comput. 2016, 15, 3087–3099. [Google Scholar] [CrossRef]
- Eiben, A.; Smith, J. Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Reeves, C.R.; Rowe, J.E. Genetic Algorithms: Principles and Perspectives: A Guide to GA Theory; Kluwer Academic Publishers: Norwell, MA, USA, 2002. [Google Scholar]
- Miller, B.L.; Goldberg, D.E. Genetic Algorithms, Tournament Selection, and the Effects of Noise. Complex Syst. 1995, 9, 193–212. [Google Scholar]
- Liao, Y.H.; Sun, C.T. An Educational Genetic Algorithms Learning Tool. IEEE Trans. Educ. 2001, 44. [Google Scholar] [CrossRef]
- Wakunda, J.; Zell, A. A new selection scheme for steady-state evolution strategies. In Proceedings of the Genetic and Evolutionary Computation Conference (GECCO), Las Vegas, NV, USA, 8–12 July 2000; pp. 794–801. [Google Scholar]
- Krajzewicz, D.; Erdmann, J.; Behrisch, M.; Bieker, L. Recent Development and Applications of SUMO—Simulation of Urban MObility. Int. J. Adv. Syst. Meas. 2012, 5, 128–138. [Google Scholar]
- Krajzewicz, D.; Hertkorn, G.; Rossel, C.; Wagner, P. SUMO (Simulation of Urban MObility)—An open-source traffic simulation. In Proceedings of the 4th Middle East Symposium on Simulation and Modelling (MESM 2002), Sharjah, UAE, 28–30 October 2002; pp. 183–187. [Google Scholar]
- Martinez, F.J.; Cano, J.C.; Calafate, C.T.; Manzoni, P. A Performance Evaluation of Warning Message Dissemination in 802.11p based VANETs. In Proceedings of the IEEE Local Computer Networks Conference (LCN), Zurich, Switzerland, 20–23 October 2009; pp. 221–224. [Google Scholar]
- Fall, K.; Varadhan, K. ns Notes and Documents. The VINT Project. UC Berkeley, LBL, USC/ISI, and Xerox PARC. 2000. Available online: http://www.isi.edu/nsnam/ns/ns-documentation.html (accessed on 1 January 2018).
- IEEE 802.11 Working Group. IEEE Standard for Information Technology—Telecommunications and Information Exchange between Systems—Local and Metropolitan Area Networks—Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 6: Wireless Access in Vehicular Environments; IEEE Standards Association: Piscataway, NJ, USA, 2010. [Google Scholar]
- Martinez, F.J.; Fogue, M.; Toh, C.; Cano, J.C.; Calafate, C.T.; Manzoni, P. Computer Simulations of VANETs Using Realistic City Topologies. Wirel. Pers. Commun. 2013, 69, 639–663. [Google Scholar] [CrossRef]
- European Telecommunications Standards Institute. Intelligent Transport Systems (ITS); Communications Architecture. ETSI EN 302 665. 2010. Available online: http://www.etsi.org/deliver/etsi_en/302600_302699/302665/01.01.01_60/en_302665v010101p.pdf (accessed on 1 January 2018).
- Fogue, M.; Garrido, P.; Martinez, F.J.; Cano, J.C.; Calafate, C.T.; Manzoni, P. A Realistic Simulation Framework for Vehicular Networks. In Proceedings of the 5th International ICST Conference on Simulation Tools and Techniques (SIMUTools), Desenzano del Garda, Italy, 19–23 March 2012; pp. 37–46. [Google Scholar]












| Representation | Integer strings [1..#Roadside Units] |
| Re-combination | 1-point crossover |
| Re-combination probability | 95% |
| Mutation probability | 1 gene/individual (avg.) |
| Parent selection | Tournament k = 2 |
| Survival selection | Steady-state |
| Generational Gap | 50% |
| Population size | 8 |
| Initialization | Random |
| Termination condition | 80 generations |
| Number of executions | 5 |
| Parameter | Value |
|---|---|
| mobility generator | Citymob for Roadmaps (C4R) [34] |
| number of vehicles | 100, 200, 300, 400 |
| simulated area | 2000 m × 2000 m |
| simulated layouts | Madrid and Valencia |
| mobility models | Downtown model [29] and Krauss [28] |
| maximum acceleration of vehicles | 1.4 m/s |
| maximum deceleration of vehicles | 2.0 m/s |
| driver reaction time () | 1 s |
| number of warning mode vehicles | 3 |
| message size | 512 bytes |
| message rate | 1 per second |
| Physical and Medium Access Control layers (PHY/MAC ) | IEEE 802.11p |
| maximum transmission range | 400 m |
| warning message priority | Access Category 3 (AC3) |
| normal message priority | Access Category 1 (AC1) |
| Number of Vehicles | Vehicle | Geographic | D-RSU | GARSUD |
|---|---|---|---|---|
| 100 | #1 | 0.834 s | 36.210 s | 0.833 s |
| #2 | - | 0.204 s | 0.839 s | |
| #3 | 0.829 s | - | 0.839 s | |
| 200 | #1 | - | - | 0.205 s |
| #2 | 13.837 s | 0.840 s | 0.838 s | |
| #3 | - | 0.221 s | 0.226 s | |
| 300 | #1 | - | - | 0.252 s |
| #2 | 1.237 s | 0.845 s | 0.850 s | |
| #3 | - | 0.860 s | 0.851 s | |
| 400 | #1 | 0.287 s | 0.227 s | 0.238 s |
| #2 | 0.722 s | 0.848 s | 0.838 s | |
| #3 | - | 0.911 s | 0.912 s |
| Number of Vehicles | Vehicle | Geographic | D-RSU | GARSUD |
|---|---|---|---|---|
| 100 | #1 | 2.861 s | 0.825 s | 0.826 s |
| #2 | 0.204 s | 0.833 s | 0.849 s | |
| #3 | 10.898 s | 0.829 s | 0.852 s | |
| 200 | #1 | - | 0.203 s | 0.231 s |
| #2 | 0.837 s | 0.876 s | 0.203 s | |
| #3 | 0.211 s | 24.221 s | 0.241 s | |
| 300 | #1 | - | 18.825 s | 0.906 s |
| #2 | 0.872 s | 10.206 s | 0.902 s | |
| #3 | 0.858 s | 6.869 s | 0.859 s | |
| 400 | #1 | 0.225 s | 2.239 s | 0.223 s |
| #2 | 0.843 s | 0.866 s | 0.841 s | |
| #3 | 0.905 s | 0.214 s | 0.831 s |
| Number of Vehicles | Vehicle | Geographic | D-RSU | GARSUD |
|---|---|---|---|---|
| 100 | #1 | 6.664 s | 15.993 s | 4.335 s |
| #2 | 11.340 s | 0.650 s | 3.653 s | |
| #3 | 6.863 s | 3.983 s | 0.839 s | |
| 200 | #1 | 13.978 s | 20.988 s | 8.313 s |
| #2 | 6.320 s | 0.868 s | 2.672 s | |
| #3 | 0.650 s | 0.658 s | 0.648 s | |
| 300 | #1 | 0.648 s | 0.652 s | 0.651 s |
| #2 | 0.643 s | 0.648 s | 0.647 s | |
| #3 | 0.652 s | 0.648 s | 0.649 s | |
| 400 | #1 | 0.650 s | 0.649 s | 0.647 s |
| #2 | 0.704 s | 0.652 s | 0.650 s | |
| #3 | 0.903 s | 0.912 s | 0.655 s |
| Number of Vehicles | Vehicle | Geographic | D-RSU | GARSUD |
|---|---|---|---|---|
| 100 | #1 | 15.984 s | 5.320 s | 3.979 s |
| #2 | 0.647 s | 0.524 s | 0.993 s | |
| #3 | 6.989 s | 7.987 s | 3.647 s | |
| 200 | #1 | 7.314 s | 11.651 s | 3.324 s |
| #2 | 15.688 s | 6.328 s | 0.993 s | |
| #3 | 0.653 s | 0.652 s | 0.654 s | |
| 300 | #1 | 0.650 s | 0.654 s | 0.656 s |
| #2 | 0.645 s | 0.646 s | 0.642 s | |
| #3 | 0.649 s | 0.654 s | 0.647 s | |
| 400 | #1 | 0.655 s | 0.649 s | 0.650 s |
| #2 | 0.647 s | 0.650 s | 0.656 s | |
| #3 | 0.655 s | 0.645 s | 0.654 s |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fogue, M.; Sanguesa, J.A.; Martinez, F.J.; Marquez-Barja, J.M. Improving Roadside Unit Deployment in Vehicular Networks by Exploiting Genetic Algorithms. Appl. Sci. 2018, 8, 86. https://doi.org/10.3390/app8010086
Fogue M, Sanguesa JA, Martinez FJ, Marquez-Barja JM. Improving Roadside Unit Deployment in Vehicular Networks by Exploiting Genetic Algorithms. Applied Sciences. 2018; 8(1):86. https://doi.org/10.3390/app8010086
Chicago/Turabian StyleFogue, Manuel, Julio A. Sanguesa, Francisco J. Martinez, and Johann M. Marquez-Barja. 2018. "Improving Roadside Unit Deployment in Vehicular Networks by Exploiting Genetic Algorithms" Applied Sciences 8, no. 1: 86. https://doi.org/10.3390/app8010086
APA StyleFogue, M., Sanguesa, J. A., Martinez, F. J., & Marquez-Barja, J. M. (2018). Improving Roadside Unit Deployment in Vehicular Networks by Exploiting Genetic Algorithms. Applied Sciences, 8(1), 86. https://doi.org/10.3390/app8010086