1. Introduction
The most common causes of sudden death are cardiovascular diseases, which are among the leading causes of death worldwide. One of the cardiovascular diseases with the highest mortality is Ventricular Fibrillation (
), which is a cardiac arrhythmia condition produced by a disorganized electrical activity in the ventricles. During
, the ventricles contract with an absence of an effective beat causing a pumping failure which could lead to a sudden death if the patient is not adequately treated within a few minutes. Defibrillation is the only definitive treatment for
. It consists of applying a high voltage electric shock on the patient’s chest, facilitating the restart of a normal electrical cardiac activity [
1,
2,
3]. However, the success of defibrillation is inversely proportional to the interval of time lapsed from the beginning of the episode to the application of the discharge.
There are many difficulties in diagnosing
: On the one hand, the intrinsic characteristics of the
signal (lack of organization, irregularity, etc.) and, on the other hand, the great similarity between VF and other cardiac pathologies such as ventricular tachycardia (
) [
4], especially in early stages of
. The differentiation between
and
is quite complex: The wrongful diagnosis of
for a patient that really suffers of
can cause serious complications at the time of applying the therapy corresponding to
(high voltage electrical discharge), as it may cause
to the patient. On the contrary, if
is incorrectly interpreted as
or any other cardiac rhythm, the result can also be dangerous for the patient’s life since the treatment would imply receiving less voltage than the appropriate level. Thus, an effective detection method for distinguishing
from
is critical in clinical research.
The electrocardiogram (ECG) is a non-invasive, low-cost examination tool that has been used as the basic method of diagnosing cardiac conduction disorders by studying the heart rate and morphology of different waves that constitute the cardiac cycle. ECG analysis is a good source of information from which different types of heart disease can be detected. Due to the fact that the ECG signal is a non-stationary random signal, the time domain analysis does not prove to be sufficiently sensitive to the distortions of the ECG waveforms. However, these methods do not always show all the information that can be extracted from the ECG signals [
5,
6], thus losing information on the frequency domain which shows additional information on the signal.
Diagnosis in the frequency domain [
7] uses methods such as the Fourier transform. Therefore, the analysis in the frequency domain allows to determine the frequencies of the signal. On the other hand, the temporary-type information of the signal is lost, which is a very limited method and is not useful for the analysis of non-stationary signals. Several studies have used mathematical models that combine temporal and spectral information in the same representation. This technique of Time-Frequency Representation (
) is very important in the treatment of non-stationary signals such as the ECG signal, as it distributes the energy of the signal in a two-dimensional time-frequency space [
8,
9]. In addition, multiple factors might alter the acquisition and recording of the ECG signal: The influence of the environment, 50–60 Hz mains interference, variations of the base line of low-frequency interference in the range of 0 Hz to 0.5 Hz [
10,
11]. On the other hand, there are disturbances of physiological origin such as those of electromyography (EMG). ECG noise reduction has been one of the main fields of research in the last decades since an adequate noise reduction allows a good pre-processing of the signal, extracting the maximum amount of information possible and eliminating ECG signal contamination from other sources.
Usually, after the initial processing of the signal, several algorithms are applied to obtain characteristics, features, or parameters which are supposed to offer a difference in value depending on the pathology. Typically, these parameters can be redundant or remove relevant information, being necessary to apply different techniques to select the most adequate. After optimisation, selected parameters are intended to serve as input to a classifier responsible for separating classes (associated to a pathology or type of rhythm, in this case), i.e. identified signal types.
In order to improve the performance of individual classifiers, the combination of classifiers (multiclassifiers) can improve the performance in separating classes. It is based on constructing a global classifier built from a set of classifiers that can provide interesting information on the representation of data compared to the results achieved using individual classifiers. There are many examples in the literature that have used the combination of classifiers focused towards the field of bioinformatics and biomedical research, geophysical analysis and remote sensing, among others. Out of the most frequently used multi classifiers, Random Forests [
12], Bagging [
8], Boosting [
13], or Random Subspaces are the most commonly employed multiclassifiers. In the case of Random Subspaces, different subsets of attributes are used to train each individual classifier. The Bagging type variety comes from using different subsets of instances to train each individual classifier. Random Forests is a substantial modification of bagging that uses Random Trees as individual classifiers. The Boosting type iteratively trains the individual classifiers, therefore, it modifies the weights of the instances that will use the next individual classifier. There are other methods such as cascading [
14], Stacking [
15], and Grading [
16].
Other examples using a combination of classifiers for ECG signal analysis can be found in the literature as a multiple classifier system [
17], a genetic ensembles of classifiers [
18], or a classification approach that uses majority voting optimized by the taguchi method [
19]. In some cases, a majority voting [
20,
21], or a combined stacking technique [
22]. Other combinations are also applied, e.g., an application of the decision tree to integrate the results of a set of individual neural classifiers (MLP, TSK, and the SVM) working in parallel [
23] or a majority voter determining the P-wave absence over seven beats [
24].
This work proposes a new strategy for the detection of whose steps are the initial processing of the signal and obtaining its time-frequency representation () with its equivalent image (). The or (both cases will be analysed) is directly entered into an individual classifier or combined, without calculating parameters or extracting features since time-frequency representation contains both temporal and spectral information from the ECG signal, allowing the classifier to have enough information for the detection of different types of cardiac pathologies in real time. Since the ECG is a temporal signal, it is not common to find works converting the temporal signal into an image and further analyse the image, some works used some geometrical features from the ECG in combination with other features entering the classification stage. Other works also extract features from a time-frequency or discrete wavelet transform, but they do not use it as an image.
In order to reach the objectives sought, the present work is structured as follows:
Section 2 describes the materials and methods, followed by
Section 3 which details the initial processing applied to the ECG signal.
Section 4 shows the extraction of information.
Section 5 presents the individual and combined classification algorithms.
Section 6 shows the standard statistical indexes, and finally,
Section 7 shows obtained results for individual and combined classifiers, and
Section 8 and
Section 9 give a comparison of results with other authors and conclusions, respectively.
7. Results
In total, 28,507 windows were generated for all obtained from the corresponding : 5309 corresponded to the class , 1987 to , 15,160 to , and 6051 to . For each class, 67% of the data were used for training, and the rest for testing. This approach is repeated by making a 5-fold cross validation: Individual and combined classifier algorithms are assessed by taking the average of these 5 iterations. A 5-fold validation was chosen amongst different z-fold possibilities after some trials, with 5-fold cross validation obtaining the lowest generalization error, thus minimizing the structural risk of classifiers. For 5-fold cross validation, each class was divided into five datasets, equal in size; four dataset were used for training and one for testing. After five iterations, all datasets served for training and testing, obtaining a more balanced result.
Different analyses were done, the first test is based on different types of individual classification algorithms, the second uses combined classification algorithms.
7.1. Results for Individual Classifiers
In this first test, individual classifiers are used. The results are obtained using four different classification algorithms:
,
,
, and
[
8,
31]. After several trials, the parameters for the classifiers were the following:
: With regularization parameter . In this case, the value is very small to account for high values in regression coefficients.
: Two hidden layers, 20 neurons in each hidden layer. Two layers allow better classification in case of a high number of inputs, as in this case. In case of a single layer, a higher number of neurons should be used.
: 600 decision trees. This was an experimental value. A higher number of trees did not produce better results.
: Euclidean distance showed a good performance, together with K = 1.
Table 1 and
Table 2 summarize the results achieved by making comparisons between the values of sensitivity, specificity, accuracy, and precision. When analyzing the values shown in the tables, it is observed that the
classifier obtained the best result, with a sensitivity of 94.97 ± 0.70%, a global specificity of 99.27 ± 0.05%, accuracy of 98.47 ± 0.01%, and an overall precision of 97.09 ± 0.14% achieved for
. For
, a sensitivity of 93.47 ± 0.19%, specificity of 99.39 ± 0.15%, accuracy 98.97 ± 0.08%, and an overall precision of 92.11 ± 0.7% was obtained.
For a complete analysis, the confusion matrices for the classes and the used algorithms were calculated (
Table 3 and
Table 4). These tables show that the main conflicts exist in pairs:
and
,
and
. Actually, since the number of segments is lower for
and
compared to normal and Others, the proportion of confusion mainly resides in
and
S, which was expected according to other algorithm results and clinical practice.
Comparing the results offered by the different algorithms, there is an important variation in the results for the sensitivities of and depending on the algorithm. For instance, if the sensitivity level for is high, the sensitivity for decreases. It can be observed that the classifier achieves the best performance for the proposed methodology due to the adequate detection and discrimination capacity of when compared against the rest of classes. However, it has a high execution time because the algorithm requires many iterations to calculate the closest distances. For the algorithm, the classes are separated by means of a surface that maximizes the margin among them, with the least number of training errors, having a computational cost much lower than that obtained with . The algorithm has less time of execution because it is based on probabilities. The Bagging creates its individual classifiers by training a system of classification on different bootstrap samples of the training set, thus retrieving a higher run time than the rest of the classifiers (except for ).
7.2. Comparative Study for the Method of Combined Classifiers
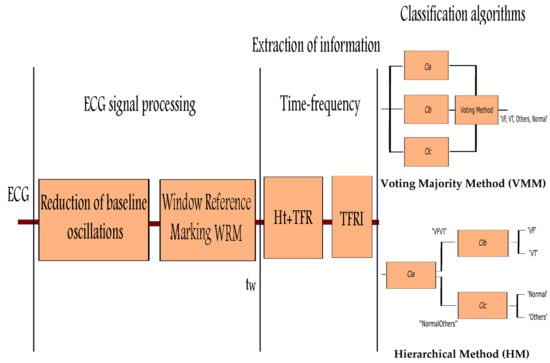
In this section, the results obtained by the combination methods are described: Voting Majority Method (VMM) and Hierarchical Method (HM) described above. In the classification tests performed, we show how the combination of classification algorithms behaves in relation to the results obtained in the previous test using individual classifiers. For proper comparison, the same data used for individual classifiers, and the same classifier parameters were used in these analyses.
In the first analysis, the Voting Majority Method (VMM) is applied using different combinations of three individual classification algorithms in parallel, the results obtained are shown in
Table 5,
Table 6,
Table 7 and
Table 8. When analyzing the results from the tables, it can be seen, in both cases, that the detection of
has significantly improved when compared with individual classifiers. However, the detection of
has decreased when compared with what those obtained by the
algorithm, which was the best individual classifier. It is concluded that the combination of classifiers do not exceed the results obtained in case of
.
In the second analysis, the Hierarchical Method (HM) is applied to three individual algorithms (
,
,
) getting the
multiclassifier where
and
are in parallel and both cascaded after
(
Figure 5). The obtained results are shown in
Table 9 and
Table 10 with confusion matrices in
Table 11,
Table 12 and
Table 13.
Since was the best individual algorithm in the detection and discrimination between and , it was chosen as . The , , algorithms are taken as for the discrimination between the classes and and the and algorithms are used as for and discrimination. Analyzing the results, it can be concluded that the combinational algorithms have a similar or better behavior than the individual in the detection of in very large datasets and high dimensionality, with a reduced execution time.
With all the results obtained, the use of combined algorithms can be recommended as the best method of classification. In addition, results obtained using the combination using HM showed better classification ratio when compared to those obtained using the algorithms individually, and other multi classifiers.
The HM obtained a good behavior in the discrimination between the classes , , , and , with a sensitivity of 95.58 ± 0.4%, a global specificity of 99.31 ± 0.08%, an accuracy of 98.6 ± 0.04%, and an overall precision of 98.25 ± 0.29% for . For , a sensitivity of 94.02 ± 0.58%, a specificity of 99.31 ± 0.08%, an accuracy of 99.14 ± 0.43%, and a precision of 98.59 ± 0.09% was obtained.
It is interesting to note that the classifier obtained a good behavior in the discrimination between the classes and , and the classifier had a good behavior in the discrimination between the classes and with a fast execution time in comparison with the individual algorithm.
Table 14 shows the average execution time of all the classification algorithms analyzed in this work. The execution time corresponds to the elapsed time between the input of a
window from the ECG signal to the generation of a classification result of the algorithm. Concerning individual classifiers, it can be appreciated that
and
have a lower computational cost than other individual algoithms, with a run time of
s and
s, respectively. For
and
,
s and
s was attained, respectively. In case of the VMM combination methods, they are the slowest among HM and individual, ranging from
ms to
ms. This is normal since all three classifiers (
,
,
) must be computed, increasing the total computation time. Actually, any VMM combination method required more computation time than the slowest individual algorithm (
). In case of HM classification methods, we obtained different computation time depending on the executed classifier (
or
) depending on the results given by the first classifier (
). For this reason we obtained a minimum and maximum computation time, ranging from
ms to
ms. Thus HM combined methods provide a high classification, together with a reduced computation time, showing their feasibility for real-time classification systems.
8. Discussion
Table 15 and
Figure 6 show the AUC values and ROC curves, respectively,
Figure 6a for
and
Figure 6b for
in case of the analyzed individual algorithms.
Table 16 and
Figure 7 show the AUC values and ROC curves, respectively, for
(
Figure 6a) and
(
Figure 6b) classification results for the VMM combination of classifiers.
Table 17 and
Figure 8 show the AUC values and ROC curves, respectively, for
(
Figure 6a) and
(
Figure 6b) classification results for the HM combination of classifiers. As shown, ROC curves are more adjusted in case of combined classifiers, especially in case of the VMM method.
Additionally, the structural risk of the classifier is important in order to determine the training robustness. A risk test is proposed by the A-test where multiple z-fold cross-validation are performed in order to assess how classification error evolves. In this case, we have also tested 9-fold cross validation for comparison purposes with 5-fold.
Figure 9 shows that very similar results are obtained for the same classifier. Specially in case of HM combined classifers, z-5 provides a slightly higher classification ratio. In any case, differences between z-5 and z-9 in the same classifier do not exceed 1% in classification value.
Since correct detection and classification of
and
is of pivotal importance for an automatic external defibrillation and patient monitoring, they should be able to distinguish
and
accurately. If
was misinterpreted as
, a high-energy defibrillation would be delivered, which could damage the heart. If
is misinterpreted as
, the low-energy cardioversion may not return the heart to its normal sinus rhythm, which could be fatal [
34]. However, clear distinction between ventricular arrhythmia rhythms and normal or other arrhythmias is required, preventing the patient to be unnecessarily exposed to an electrical cardioversion.
As previous results show, the proposed methods obtain a high accuracy, not only in and separation but also in and . This fact leads to further separate the class into other sub-classes where different heart pathologies could also be detected: Premature Ventricular Complex (PVC) in bigeminy or trigeminy, hypertrophy, idioventricular Rhythms, asystoles, etc. Thus, using a new classifier level, all rhythms detected as could enter into a new classification process in order to discern among other cardiac pathologies.
Table 18 compares results with different studies in the bibliography to check to what extent the obtained data support our hypothesis. Although different works are roughly comparable, we set two different groups for better comparison: those works aiming to distinguish between
and
, and those works classifying multiple rhythms.
For the first group, Xie et al. [
39] used approximate entropy to distinguish between
and
with performance ratios of Sens = 91.84% to
, Spe = 90.2%, Acc = 91.0%, using similar signal sources than our work. In addition, they also proposed a modified version using fuzzy similarity-based approximate entropy that, in turn, got high performance ratios (Sens = 97.98% to
, Spe = 97.03%, Acc = 97.5%). Although we obtained higher values, to make a fair comparison between both analysis, it has to be taken into account that Xie used representative and clean episodes of
and
as input data, in front of our work that used a multiclass scheme, classifying four types of rhythms and considering complete patient’s registers as the input signal. The same happens for other studies distinguishing between
and
rhythms; Kaur and Singh [
40] used approximate entropy with Empirical Mode Decomposition (EMD) and a more reduced dataset than Xie, having good performance values (Sens = 90.47 to
, Spe = 91.66%, Acc = 91.2%). Later, Xia et al. [
38] also used, in the same line, Lempel-Ziv Complexity and EMD in the same conditions that Xie did before, using a representative number of clean episodes of each pathology, and they also got high performance ratios (Sens = 98.15% to
, Spe = 96.01%, Acc = 97.1%). The same occurred to Li et al. [
37] using SVM where Sens = 96.20% to
, Spe = 96.20%, and Acc = 96.3%, for a 2 s window, was obtained; in this case, a sensitive different set of source signals was used. Other works provides good performance ratios distinguishing between
and
when applied to compressed ECG signals [
41]. In all cases, our performance results are slightly or sensitive better.
As a second group of comparable works we can find those aiming to distinguish normal sinus (N) apart from
or
. Within this group, Tan et al. [
42] obtained good accuracy ratios (Acc(
) = 90.9%, Acc(
) = 84.0%, Acc(N) = 100%) using a type-2 fuzzy logic-based classifier for a three class multiclass classification (
,
and
). Tan also described the results of using a SOM neural network with poor VT accuracy. Later, Phong et al. [
43] followed the same line implementing another multiclass classifier using a type-2 TSK fuzzy system, with the same three classes than Tan used; in this case, with better accuracy ratios (Acc(
) = 93.3%, Acc(
) = 92.0%, Acc(N) = 100%). They also tried a a type-2 Mandami fuzzy system with lower values.
Other works analyse a binary distinction between
and non-
rhythms. Verma et al. [
44] used 17 features: Morphological, spectral, and complexity. Here, the random forest classifier has been used for discrimination between
category and non-
category, with Acc = 94.79%, Sens = 95.04%, Spe = 94.78%. In [
45], they used 13 parameters accounting for temporal (morphological), spectral, and complexity features of the ECG signal, using an SVM to distinguish between
and non-
categories with Sens = 95%, Spe = 99%. In another attempt [
46], different heart rhythms were detected and classified into the
and non-
types using six features, four are derived from image-based phase plot analysis, one is derived in the frequency domain, and the last reflects the nonlinear characteristics of a data segment, values of (Acc = 95.3%, Sens = 94.5%, Spe = 94.2%) and (Acc = 90.4%, Sens = 91.6%, Spe = 89.3%) using binary decision tree (BDT) and the SVM, respectively. The algorithm proposed by Tripathy et al. [
47], using digital Taylor-Fourier transform (DTFT) features of ECG signals and least square support vector machine (LS-SVM) with linear and radial basis function (RBF) kernels for detection of
and non-
arrhythmia episodes, obtained performance values of Acc = 83.75%, Sens = 85.20%, Spe = 82.46%.
Other authors have classified the ECG signal segments into
and non-
. These results are not directly comparable with those in the previous table since they provide a binary output. However, we include them since they are interesting to see how simpler two-class classification still provides similar results to those obtained in this work. Zhou et al. [
48] classified the ECG signal segments into the normal sinus rhytnm (NSR) or arrhythmic shockable classes
. The classification is based on Time-Delay Transform (TDT) of the signals and a neural network with Weight Fuzzy Membership Functions (NEWFM). They obtained Acc = 89.5%, Sens = 73.6%, and Spe = 93.5%. Xu et al. [
49] detected
using boosted classification and regression tree (Boosted-CART) obtaining Acc = 98.29%, Sens = 97.32%, and Spe = 98.95%. Other studies that have also used the class
[
1] have evaluated both time domain (e.g., energy, permutation entropy) and frequency domain (e.g., renyi entropy) features. The classification is done by using a Random Forest (RF) classifier aiming to identify shockable and non-shockable ventricular arrhythmia with CUDB and MITDB databases with results of Acc = 97.23%, Sens = 96.54%, Spe = 97.97% [
50]. Thirteen time-frequency and statistical features were extracted and applied to the C4.5 classifier [
51], resulting in Acc = 97.02%, Sens = 90.97%, Spe = 97.86% for
detection (including ventricular flutter). In Kimmo et al. [
52], gaussian processes were used to detect
,
, and
episodes (all three considered in the same class) extracting 15 metrics obtaining Acc = 91%, Sens = 89%, Spe = 88%.
9. Conclusions
As mentioned above, one of the main causes of sudden death is caused by the VF arrhythmia [
3,
53]. The rapid and correct detection of
and
is of fundamental importance both for the use of an automatic external defibrillator and for monitoring the patient. In order to obtain a reliable algorithm to discriminate between the different arrhythmias, an attempt was made to perform this detection task using the lowest computational load. The methodology uses the ECG to monitor biomedical signals that have different morphological and spectral characteristics.
We propose the analysis of the ECG signal for the real-time detection of the onset of ventricular fibrillation using a time-frequency method [
7,
54]. Reduction of network interference and other noises, which correspond to high frequency noises in these signals was carried out. After performing the steps above, the data matrix of each
is converted to an image (
) corresponding to the different cardiac pathologies of the processed ECG signal, allowing to obtain an appropriate representation capable of providing useful information about the problem to be solved and allowing practical applications to the diagnosis in real time. The novelty of this work lies in the fact of using a reference mark
to establish an analysis window
, obtaining a time-frequency representation and its associated image (
and
matrices, respectively) which are used as input to a combined classification algorithm without calculation of additional parameters for the classifier. This fact avoids the extraction of characteristics and thus, the loss of relevant information to discriminate between the different classes. Additionaly, we propose the use of combined specialized classifiers to improve classification. An analysis of several combination methodologies, and a comparative study between the individual performance of the
,
,
, and
algorithms was done. All of these individual and combined classifier algorithms were trained with the cross-validation method and evaluated based on sensitivity, specificity, accuracy, precision, and execution time.
Using the strategy, we concluded that, using z-5 cross validation, the individual classifier achieves good results retrieving a sensitivity of 94.97 ± 0.70%, a specificity of 99.27 ± 0.05%, an accuracy of 98.47 ± 0.01%, and a precision of 97.09 ± 0.14% for . In case of , a sensitivity of 93.47 ± 0.19%, specificity of 99.39 ± 0.15%, accuracy of 98.97 ± 0.08%, and precision of 92.11 ± 0.7%, with a running time s. Using the strategy with combined classifiers in hierarchical form (HM) achieved a sensitivity of 95.58 ± 0.40%, specificity of 99.31 ± 0.08%, 98.6 ± 0.04% accuracy, and a precision of 98.25 ± 0.29% for , with a sensitivity of 94.02 ± 0.58%, specificity of 99.31 ± 0.08%, accuracy of 99.14 ± 0.43%, and a precision of 98.59 ± 0.09% for , with execution time between s and s.
Different classifier robustness and classification analysis are performed to validate results: Sensibility, specificty, accuracy, precision, confusioin matrices, ROC, AUC, and A-test. All these analyses show that the used methodology is adequate and congruent results are obtained.
Taking into consideration the performed study, we have concluded that the use of combined classifiers is the best way to integrate the information since they provide stronger and efficient estimates than a single classifier. The proposed methodology provides useful information for the detection of in real time with a low computational time, discriminating from the rest of the cardiac pathologies satisfactorily. This fact significantly improves the possibilities of correct diagnosis of the patient when presenting an episode with any of these arrhythmias.