Seismic Analysis of Steel Solid Web Girder-RC Tubular Column Hybrid Structure
Abstract
:1. Introduction
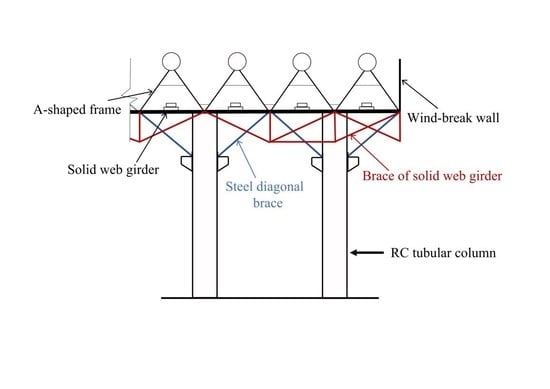
2. Case Study
3. Numerical Approaches and Validation
3.1. Simulation of RC Tubular Columns
3.2. Simulation of Steel Components
3.3. Validation of the Modelling Approaches
3.4. Numerical Model of the Steel Solid Web Girder-RC Tubular Column Hybrid Structure
4. Numerical Results and Discussion
4.1. Dynamic Characteristics
4.2. Nonlinear Dynamic Time-History Analysis
4.3. Lateral Deformation Performance
4.4. Lateral Stiffness Deterioration and Damage Analysis
5. Conclusions
- (1)
- This paper proposes the modelling approaches for this kind of supporting structural system. The comparison between the FE numerical results and test results of a model structure indicated that the proposed FE modeling approaches are reasonable to simulate the seismic behavior of this kind of steel-concrete hybrid structure.
- (2)
- Due to the small torsional stiffness and the nonuniform distribution characteristics of stiffness and mass in vertical direction, the first vibration mode of steel solid web girder-RC tubular column hybrid structure was torsion. The calculation results of the first torsion to translation period ratio of this hybrid structure showed that it was greater than the upper limit value recommended by the China seismic design code. This indicated that the torsion effect can not be ignored in the design for this kind of hybrid structure. In addition, the shear-weight ratio of this hybrid structure under the frequent earthquake was 0.059, which was greater than the lower limit value recommended by the China technical specification for concrete structures of tall building.
- (3)
- The numerical results of lateral deformation performance showed that it was shear mode for this hybrid structure. The maximum drift ratios on the top of column under the frequent and basic earthquakes were 0.06 and 0.15, respectively. They were less than the upper limit value recommended by the China technical code for the design of civil structure of fossil-fired power plant. In addition, the numerical results showed that the damage mainly occurred on the RC tubular columns, while the steel components of this hybrid structure did not yield under the earthquakes. This coincided with the expected design results considering the normal use of the industrial units directly supported by the steel solid web girder platform and A-shaped frames. Moreover, under the very rare earthquake, the residual lateral stiffness ratio and the maximum tensile damage index of this hybrid structure was 39% and 0.90. This indicated that the structure was severely damaged but did not collapse. Overall, the numerical investigations showed that the seismic performance of steel solid web girder-RC tubular column hybrid structure could satisfy the design requirements in the strong earthquake region.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dall’Asta, A.; Leoni, G.; Morelli, F.; Salvatore, W.; Zona, A. An innovative seismic-resistant steel frame with reinforced concrete infill walls. Eng. Struct. 2017, 141, 144–158. [Google Scholar] [CrossRef]
- Dall’Asta, A.; Leoni, G.; Zona, A.; Hoffmeister, B.; Bigelow, H.; Degée, H.; Braham, C.; Bogdan, T.; Salvatore, W.; Morelli, F.; et al. Innovative Hybrid and Composite Steel-Concrete Structural Solutions for Building in Seismic Area; Final Report EUR 26932 EN; European Commission: Brussels, Belgium, 2015. [Google Scholar]
- Hajjar, J.F. Composite steel and concrete structural systems for seismic engineering. J. Constr. Steel Res. 2002, 58, 703–723. [Google Scholar] [CrossRef]
- Deierlein, G.G.; Noguchi, H. Overview of US-Japan research on the seismic design of composite reinforced concrete and steel moment frame structures. J. Struct. Eng. 2004, 130, 361–367. [Google Scholar] [CrossRef]
- Sivandi-Pour, A.; Gerami, M.; Kheyroddin, A. Uniform damping ratio for non-classically damped hybrid steel concrete structures. Int. J. Civ. Eng. 2016, 14, 1–11. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Tran, V.T.; Hjiaj, M. Hybrid RC-steel members under bending and shear: Experimental investigation and design model. J. Constr. Steel Res. 2017, 138, 837–850. [Google Scholar] [CrossRef]
- Keo, P.; Lepourry, C.; Somja, H.; Palas, F. Behavior of a new shear connector for U-shaped steel-concrete hybrid beams. J. Constr. Steel Res. 2018, 145, 153–166. [Google Scholar] [CrossRef]
- Bai, Y.T.; Bai, G.L. Pseudo-dynamic and quasi-static testing of an irregular steel concrete composite frame with wing walls. Int. J. Struct. Stab. Dyn. 2016, 16, 1450095. [Google Scholar] [CrossRef]
- Wang, B.; Bai, G.L.; Dai, H.J.; Zhu, J.N.; Li, H.X. Research on mechanical properties of abnormal SRC joints with short-limb shear walls. Eng. Mech. 2014, 31, 68–75. (In Chinese) [Google Scholar]
- Wang, B.; Bai, G.L.; Liu, L.; Dai, H.J. Elastic-plastic seismic response and anti-seismic lines of SRC frame-bent hybrid structure. J. Vib. Shock 2014, 33, 46–52. (In Chinese) [Google Scholar]
- Bai, G.L.; Zhu, L.H.; Zhao, C.L.; Li, H.X. Model test on behavior of direct air cooled condenser support plat form under service load and earthquake action. J. Build. Struct. 2008, 10, 42–49. (In Chinese) [Google Scholar]
- Yao, Z.L.; Bai, G.L.; Dang, F.N.; Li, H.X. Study on seismic behavior of a steel truss-reinforced concrete column structure. J. Build. Struct. 2011, 32, 30–36. (In Chinese) [Google Scholar]
- Dai, H.J. Study on Seismic Performance Experiment and Methods of the Steel Space Truss-Umbrella Brace Air-Cooled Condenser Structure System. Ph.D. Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2013. (In Chinese). [Google Scholar]
- Wang, B.; Dai, H.J.; Wu, T.; Bai, G.L.; Bai, Y.T. Experimental investigation on seismic behavior of steel truss-RC column hybrid structure with steel diagonal braces. Appl. Sci. 2018, 8, 131. [Google Scholar] [CrossRef]
- Wang, B.; Wu, T.; Dai, H.J.; Bai, G.L. Numerical Study on the Seismic Performance of a Steel–Concrete Hybrid Supporting Structure in Thermal Power Plants. Appl. Sci. 2018, 8, 294. [Google Scholar] [CrossRef]
- Liu, L. Optimization and Selection of Large-Capacity Unit for Air-Cooling Island Structure; Research Report; Jiangsu Shuangliang Eco-Energy Group: Wuxi, China, 2012. (In Chinese) [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Seismic Design of Buildings (GB 50011-2010); China Architecture and Building Press: Beijing, China, 2016. (In Chinese)
- General Administration of Quality Supervision. Inspection and Quarantine of the People’s Republic of China; Standardization Administration of the People’s Republic of China; Seismic Ground Motion Parameters Zonation Map of China (GB 18306-2015); China Zhijian Publishing House; China Standards Press: Beijing, China, 2015. (In Chinese)
- Nascimbene, R. Numerical model of a reinforced concrete building: Earthquake analysis and experimental validation. Period. Polytech. Civ. Eng. 2015, 59, 521–530. [Google Scholar] [CrossRef]
- Nascimbene, R. Towards non-standard numerical modeling of thin-shell structures: Geometrically linear formulation. Int. J. Comput. Methods Eng. Sci. Mech. 2014, 15, 126–141. [Google Scholar] [CrossRef]
- Brunesi, E.; Nascimbene, R. Extreme response of reinforced concrete buildings through fiber force-based finite element analysis. Eng. Struct. 2014, 69, 206–215. [Google Scholar] [CrossRef]
- Nascimbene, R. An arbitrary cross section, locking free shear-flexible curved beam finite element. Int. J. Comput. Methods Eng. Sci. Mech. 2013, 14, 90–103. [Google Scholar] [CrossRef]
- Abaqus Documentation and User Manua, version 6.10; Dassault Systemes: Vélizy-Villacoublay, France, 2010.
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of Concrete Structures (GB50010-2010); China Architecture and Building Press: Beijing, China, 2011. (In Chinese)
- Sidoroff, F. Description of Anisotropic Damage Application to Elasticity; IUTAM Colloquium on Physical Nonlinearities in Structural Analysis; Springer: Berlin, Germany, 1981; pp. 237–244. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical Specification for Concrete Structures of Tall Building (IGJ3-2010); China Architecture and Building Press: Beijing, China, 2010. (In Chinese)
- National Energy Administration of the People’s Republic of China. Technical Code for the Design of Civil Structure of Fossil-Fired Power Plant (DL 5022-2012); China Plan Press: Beijing, China, 2012. (In Chinese)
- Longo, A.; Montuori, R.; Piluso, V. Moment frames—Concentrically braced frames dual systems: Analysis of different design criteria. Struct. Infrastruct. Eng. 2016, 12, 122–141. [Google Scholar] [CrossRef]
- Montuori, R.; Muscati, R. Smart and simple design of seismic resistant reinforced concrete frame. Compos. Part B 2017, 115, 360–368. [Google Scholar] [CrossRef]
- Montuori, R.; Sagarese, V. The use of steel rbs to increase ductility of wooden beams. Eng. Struct. 2018, 169, 154–161. [Google Scholar] [CrossRef]













| Component | Material | Strength Grade | Location | Cross Section (mm) | |
|---|---|---|---|---|---|
| Tubular column | Concrete | C40 | External diameter | 4000 | |
| Wall thickness | 400 | ||||
| Steel rebar | HRB400 | Longitudinal rebar | Φ25 | ||
| HPB300 | Circular stirrup | Φ10 | |||
| Steel solid web girder platform | Steel | Q345 | Solid web girder | Main direction | H1300 × 450 × 16 × 22 |
| Secondary direction | H1300 × 450 × 16 × 22 | ||||
| Brace of solid web girder | TUB250 × 250 × 12 | ||||
| Steel diagonal brace | Diagonal brace | TUB450 × 450 × 20 | |||
| A-shaped frame | Horizontal beam | HM390 × 300 | |||
| Diagonal column | HW250 × 250 | ||||
| Mode | Natural Period (s) | Mode Shapes | Participating Mass Coefficient | ||
|---|---|---|---|---|---|
| X Direction | Y Direction | RZ Direction | |||
| 1 | 1.291 | Torsion | 0.001 | 0.000 | 0.976 |
| 2 | 1.251 | Y-direction translation | 0.987 | 0.000 | 0.001 |
| 3 | 1.239 | X-direction translation | 0.000 (0.988) | 0.986 (0.986) | 0.977 (0.977) |
| Hazard Level (PGA) | Frequent Earthquake (0.07 g) | Basic Earthquake (0.20 g) | Rare Earthquake (0.40 g) | Very Rare Earthquake (0.62 g) | ||||
|---|---|---|---|---|---|---|---|---|
| Positive (+) | Negative (−) | Positive (+) | Negative (−) | Positive (+) | Negative (−) | Positive (+) | Negative (−) | |
| Maximum base shear force (kN) | 18,361 | 15,741 | 29,612 | 32,927 | 43,055 | 41,666 | 60,826 | 61,718 |
| Shear-weight ratio | 0.059 | 0.050 | 0.094 | 0.105 | 0.137 | 0.133 | 0.194 | 0.197 |
| Hazard Level (PGA) | Maximum Lateral Displacement (mm) | Maximum Drift Ratio (%) | ||
|---|---|---|---|---|
| Top of A-Shaped Frame | Top of Column | Top of A-Shaped Frame | Top of Column | |
| Frequent earthquake (0.07 g) | 36.04 | 31.16 | 0.06 | 0.06 |
| Basic earthquake (0.20 g) | 83.71 | 73.26 | 0.14 | 0.15 |
| Rare earthquake (0.40 g) | 149.25 | 143.65 | 0.24 | 0.29 |
| Very rare earthquake (0.62 g) | 263.45 | 259.02 | 0.43 | 0.52 |
| Hazard Level (PGA) | A-Shaped Frame | Solid Web Girder | Brace of Solid Web Girder | Steel Diagonal Brace |
|---|---|---|---|---|
| Frequent earthquake (0.07 g) | 72 | 98 | 88 | 115 |
| Basic earthquake (0.20 g) | 112 | 156 | 117 | 173 |
| Rare earthquake (0.40 g) | 167 | 211 | 144 | 243 |
| Very rare earthquake (0.62 g) | 207 | 253 | 167 | 276 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, H.; Wang, B. Seismic Analysis of Steel Solid Web Girder-RC Tubular Column Hybrid Structure. Appl. Sci. 2018, 8, 2095. https://doi.org/10.3390/app8112095
Dai H, Wang B. Seismic Analysis of Steel Solid Web Girder-RC Tubular Column Hybrid Structure. Applied Sciences. 2018; 8(11):2095. https://doi.org/10.3390/app8112095
Chicago/Turabian StyleDai, Huijuan, and Bo Wang. 2018. "Seismic Analysis of Steel Solid Web Girder-RC Tubular Column Hybrid Structure" Applied Sciences 8, no. 11: 2095. https://doi.org/10.3390/app8112095
APA StyleDai, H., & Wang, B. (2018). Seismic Analysis of Steel Solid Web Girder-RC Tubular Column Hybrid Structure. Applied Sciences, 8(11), 2095. https://doi.org/10.3390/app8112095