Novel Boundary Edge Detection for Accurate 3D Surface Profilometry Using Digital Image Correlation
Abstract
:1. Introduction
2. Methodology of the Random-Speckle Optical Detection and Processing Algorithm
2.1. Principle of Digital Imaging Correlation (DIC)
2.2. Normalized Cross-Correlation (NCC) for Edge Detection
| Algorithm 1 | |
| Input: Standard-height template database T and measured speckle image R. | |
| Output: 3D profiles of objects | |
| 1 | Implement normalized cross-correlation digital image correlation (NCC DIC) to generate point clouds. |
| 2 | Segment point clouds into individual measured objects. |
| 3 | Calculate the mean and standard deviation of the correlation coefficient of the measured point and use the mean as the threshold in the following search. |
| 4 | Estimate the edge boundary of each measured point using the geometry relationship of the point with its eight neighboring points. |
| 5 | Edge point search: |
| 5.1 | Define the next inspection point according to the relationship of the point with its neighbors. |
| 5.2 | Define the subset of inspection points according to the relationships of the points with their neighbors. |
| 5.3 | Perform NCC between the subset of inspection points and the corresponding standard-height templates. |
| 5.4 | Update the edge as an inspection point if its NCC result is larger than the current one. |
| 6 | Stop the edge point search when there is no more inspection points. |
2.3. Initial Edge Point
2.4. Search Strategy for Accurate Edge Points
2.5. Criterion for Edge Detection
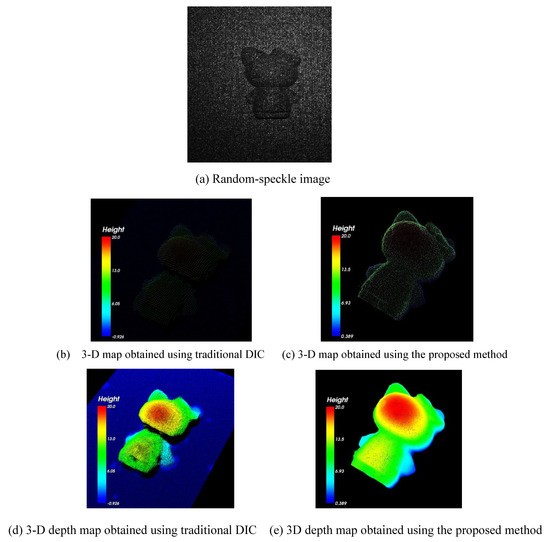
3. Experimental Results and Accuracy Analyses
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Andersen, M.R.; Jensen, T.; Lisouski, P.; Mortensen, A.K.; Hansen, M.K.; Gregersen, T.; Ahrendt, P. Kinect Depth Sensor Evaluation for Computer Vision Applications; Technical Report; Aarhus University: Aarhus, Denmark, 2012. [Google Scholar]
- McNeil, S.R.; Sutton, M.A.; Miao, Z.; Ma, J. Measurement of surface profile using digital image correlation. Exp. Mech. 1997, 37, 13–20. [Google Scholar] [CrossRef]
- Sjödahl, M.; Synnergren, P. Measurement of shape by using projected random patterns and temporal digital speckle photography. Appl. Opt. 1999, 38, 1990–1997. [Google Scholar] [CrossRef] [PubMed]
- Lecompte, D.; Smits, A.; Bossuyt, S. Quality assessment of speckle patterns for digital image correlation. Opt. Lasers Eng. 2006, 44, 1132–1145. [Google Scholar] [CrossRef] [Green Version]
- Schreier, H.W.; Sutton, M.A. Systematic errors in digital image correlation due to under matched subset shape functions. Exp. Mech. 2002, 42, 303–310. [Google Scholar] [CrossRef]
- Pan, B.; Lu, Z.; Xie, H. Mean intensity gradient: An effective global parameter for quality assessment of the speckle patterns used in digital image correlation. Opt. Lasers Eng. 2010, 48, 469–477. [Google Scholar] [CrossRef]
- Pan, B.; Xie, H.; Wang, Z.; Qian, K.; Wang, Z. Study on subset size selection in digital image correlation for speckle patterns. Opt. Express. 2008, 16, 7037–7048. [Google Scholar] [CrossRef]
- Crammond, G.; Boyd, S.W.; Dulieu-Barton, J.M. Speckle pattern quality assessment for digital image correlation. Opt. Lasers Eng. 2013, 51, 1368–1378. [Google Scholar] [CrossRef]
- García, J.; Zalevsky, Z. Three-dimensional mapping and range measurement by means of projected speckle patterns. Appl. Opt. 2008, 47, 3032–3040. [Google Scholar] [CrossRef] [PubMed]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Stoilov, G.; Kavardzhikov, V.; Pashkouleva, D. A comparative study of random patterns for digital image correlation. J. Theor. Appl. Mech. Pol. 2012, 42, 55–66. [Google Scholar] [CrossRef]
- Poissant, J.; Barthelat, F. A novel “subset splitting” procedure for digital image correlation on discontinuous displacement fields. Exp Mech. 2010, 50, 353–364. [Google Scholar] [CrossRef]
- Dai, H.; Su, X. Shape measurement by digital speckle temporal sequence correlation with digital light projector. Opt. Eng. 2001, 40, 793–800. [Google Scholar] [CrossRef]
- Wang, G.; Yin, X.; Pei, X.; Shi, C. Depth estimation for speckle projection system using progressive reliable points growing matching. Appl. Opt. 2013, 52, 516–524. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Wang, G.; Shi, C.; Liao, Q. Efficient active depth sensing by laser speckle projection system. Opt. Eng. 2014, 53, 013105. [Google Scholar] [CrossRef] [Green Version]
- Le, M.-T.; Chen, L.-C.; Lin, C.-J. Reconstruction of accurate 3-D surfaces with sharp edges using digital structured light projection and multi-dimensional image fusion. Opt. Lasers Eng. 2017, 96, 17–34. [Google Scholar] [CrossRef]
- Chen, L.-C.; Liang, C.-W.; Tseng, H.-Y.; Lin, S.-T. Accurate 3-D surface profilometry using novel boundary edge detection on digital image correlation. Appl. Mech. Mater. 2017, 870, 295–302. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.J.; Schreier, H.W. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications; Springer: New York, NY, USA, 2009. [Google Scholar]
- Chen, L.-C.; Nguyen, T.-H.; Lin, S.-T. Viewpoint-independent 3-D object segmentation for randomly stacked objects using optical object detection. Meas. Sci. Technol. 2015, 26, 105202. [Google Scholar] [CrossRef]


















| Method | CMM (A) | Traditional DIC (B) | Developed Approach | ||||
|---|---|---|---|---|---|---|---|
| Case | Mean Diameter or Width (mm) | Mean Diameter/Width (mm) | Mean Diameter or Width (mm) (C) | Standard Deviation (µm) | Measurement Error (%) (D) | Measurement Improvement (%) (E) | |
| Circular plate (diameter) | 45.473 | 41.513 | 45.253 | 267 | 0.4% | 1800% | |
| Gauge block (width) | 29.98 | 22.97 | 29.662 | 315 | 1.06% | 2204% | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.-C.; Liang, C.-W. Novel Boundary Edge Detection for Accurate 3D Surface Profilometry Using Digital Image Correlation. Appl. Sci. 2018, 8, 2541. https://doi.org/10.3390/app8122541
Chen L-C, Liang C-W. Novel Boundary Edge Detection for Accurate 3D Surface Profilometry Using Digital Image Correlation. Applied Sciences. 2018; 8(12):2541. https://doi.org/10.3390/app8122541
Chicago/Turabian StyleChen, Liang-Chia, and Ching-Wen Liang. 2018. "Novel Boundary Edge Detection for Accurate 3D Surface Profilometry Using Digital Image Correlation" Applied Sciences 8, no. 12: 2541. https://doi.org/10.3390/app8122541
APA StyleChen, L. -C., & Liang, C. -W. (2018). Novel Boundary Edge Detection for Accurate 3D Surface Profilometry Using Digital Image Correlation. Applied Sciences, 8(12), 2541. https://doi.org/10.3390/app8122541