This section presents background on the underlying theory, mathematical constructs, definitions, algorithms, and the framework.
Definition 1 covers the theory of LT unit, which works as a main coordinator assisting and regulating all the sub-units of eMLEE engine such as eFES. It inherently is based on parallel processing at a low level. While the classifier is in the learning process, LT object (in parallel) performs the measurements, records it, updates it as needed, and then feeds the learning process back. During classifier learning, LT object (governed by LT algorithm, outside of scope of this paper, but will be available as an API) creates a logical table (with rows and columns) where it adds or removes the entry of each feature as a weighted function, while constantly measuring the outcome of the classifier learning.
Definition 2 covers the creation of the feature set from raw input via random process, as shown above. As discussed earlier, it uses 3D modeling using x, y, and z coordinates. Each feature is quantized based on the scoring of these coordinates (x being representative of overfit, y being underfit and z being an optimum fit).
Definition 3 covers the core functions of this unit to quantify the scoring of the features, based on their redundancy and irrelevancy. It does this in a unique manner. It should be noted that not every irrelevant feature with high score will be removed by the algorithm. That is the beauty of it. To increase the generalization of such model with a diverse dataset that it has not seen during test (i.e., prediction), features are quantified, and either kept, removed, or put on the waiting list for re-processing of addition or removal evaluation. The benefit of this approach is that it will not do injustice to any feature without giving a second chance later in the learning process. This is because features, once aggregated with a new feature or previously unknown feature, can dramatically improve scores to participate in the learning process. However, the deep work of “unknown feature extraction” is kept for future work, as discussed in the future works section.
Definition 4 utilizes definition 1 to 3 and introduces a global and local gain functions to evaluate the optimum feature-set. Therefore, the predictor features, accepted features, and rejected features can be scored and processed.
Definition 5 finally covers the weight function to observe the 3D weighted approach for each feature that passes through all the layers, before each feature is finally added to the list of the final participating features.
The rest of the section is dedicated to the theoretical foundation of mathematical constructs and underlying algorithms.
3.1. Theory
eFES model manifests itself into specialized optimization goals of the features in the datasets. The most crucial step of all is the Extended Feature Engineering (EFE) that we refer when we build upon existing EF techniques. These five definitions help build the technical mechanics of the proposed model of eFES unit.
Definition 1. Let there be a Logical Table (LT) module that regulates the ML process during eFES constructions. Let LT have 3D coordinates as x, y, and z to track, parallelize, and update the x ← overfit(0:1), y ← underfit(0:1), z ← optimumfit(−1:+1). Let there be two functions, Feature Adder as +𝔽, and Feature Remover as −𝔽, based on linearity of the classifier for each feature under test for which the RoOpF (Rule. 1) is valid. Let Lt. RoOpF > 0.5 to be considered of acceptable predictive value.
eFES LT module builds very important functions at initial layers for adding a good fit feature and removing a bad fit feature from the set of features available to it, especially when algorithm blend is being engineered. Clearly, not all features will have an optimum predictive value and thus identifying them will count towards optimization. The feature adder function is built as:
The feature remover function is built as:
Very similar to
k-means clustering [
12] concept, that is highly used in unsupervised learning, LT implements feature weights mechanism (FWM) so it can report a feature with high relevancy score and non-redundant in a quantized form. Thus, we define:
Illustration in
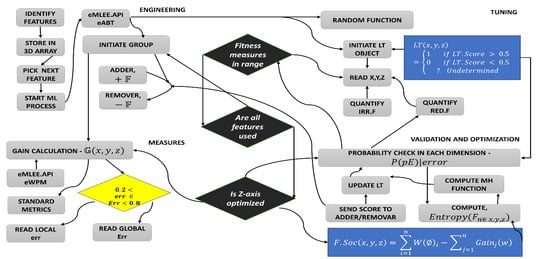
Figure 4 shows the concept of LT modular elements in 3D space as discussed earlier.
Figure 5 shows the variance of the LT.
Figure 6 shows that it is based on binary weighted classification scheme to identify the algorithm for blending and then assign a binary weight accordingly in LT logical blocks. The diamond shape shows the err distribution that is observed and recorded by LT module as new algorithm is added or existing is removed. The complete mathematical model for eFES LT is beyond the scope of this paper. We finally provide the eFES LT functions as:
where
err = local error (LE),
Err = global error (GE).
f (
x,
y,
z) is the main feature set in ‘F’ for 3D.
RULE 1If (LTObject.ScoFunc (A (i) > 0.5) Then
Assign “1”
Else Assign “0”
PROCEDURE 1
Execute LT.ScoreMetrics (Un.F, Ov.F)
Compute LT.Quantify (*LT)
Execute LT.Bias (Bias.F, *)
*_Shows the pointer to the LT object.
Definition 2. Fn = {F1, F2, F3, … …, Fn} indicates all the features appears in the dataset, where each feature Fi ∈ Fn|fw ≥ 0. fw indicates the weighted feature value in the set. Let Fran (x,y,z) indicates the randomized feature set.
We estimate the cost function based on randomized functions. Las Vegas and Monte Carlo algorithms are popular randomized algorithms. The key feature of the Las Vegas algorithm is that it will eventually have to make the right solution. The process involved is stochastic (i.e., not deterministic) and thus guarantee the outcome. In case of selecting a function, this means the algorithm must produce the smallest subset of optimized functions based on some criteria, such as the accuracy of the classification. Las Vegas Filter (LVS) is widely used to achieve this step. Here we set a criterion in which we expect each feature at random gets a random maximum predictive value in each run. ∅ shows the maximum inconsistency allowed per experiment.
Figure 5 shows the cost function variation in LT object for each coordinate.
PROCEDURE 2Scorebest ← Import all attributes as ‘n’
Costbest ← n
For j ← 1 to Iterationmax Do
Cost ← Generate random number between 0 and Costbest
Score ← Randomly select item from Cost feature
If LT.InConsistance (Scorebest, Training Set) ≤ ∅ Then
Scorebest ← Score
Costbest ← C
Return (Scorebest)
Definition 3.
Let lt.IrrF and lt.RedF be two functions to store the irrelevancy and redundancy score of each feature for a given dataset.
Let us define a Continuous Random Vector CRV ∈ QN, and Discrete Random Variable DRV ∈ H = {h1,h2,h3,……..,hn}. The density function of the random vector based on cumulative probability is P(CRV) = PH(hi)p CRV|DRV, PH(hi) being a priori probability of class.
As we observe that the higher error limit (e) (err, green line, round symbol) and lower error limit (E), (Err, blue line, square symbol) bound the feature correlation in this process. Our aim is to spread the distribution in z-dimension for optimum fitting as features are added. The red line (diamond symbol) that separates the binary distribution of Redundant Feature (Red.F) and Irrelevant Features (Irr.F) based on error bounds. The green and red lines define the upper and lower limit of the error, in which all features correlate. Here, we build a mutual information (MI) function [
14] so we can quantify the relevance of a feature upon other in the random set and this information is used to build the construct for
Irr.F, since once our classifier learns, it will mature the
Irr.F learning module as defined in the Algorithm 1.
We expect
MI ← 0, for features to be statistically independent, so we build the construct in which the MI will be linearly related to the entropies of the features under test for
Irr.F and
Red.F, thus:
We use the following construct to develop the relation of ‘
Irr.F’ and ‘
Red.F’ to show the irrelevancy factor and Redundant factor based on binary correlation and conflict mechanism as illustrated in above table.
Definition 4.
Globally in 3-D space, there exist three types of features types (variables), as predictor features:, and accepted features to beand rejected features to be, in which, global gain for all experimental occurrence of data samples. ‘’ being the global gain (GG). ‘’ being the local gain (LG). Let PV be the predictive value. Accepted features are , strongly relevant to the sample data set , if there exist at-least one x and z or y and z plane with score , AND a single feature is strongly relevant to the objective Function ‘ObF’ in distribution ‘d’ if there exist at-least a pair of example in data set {, such that d ( and d (. Let correspond to the acceptable maximum 3-axis function for possible optimum values of x, y, and z respectively.
We need to build an ideal classifier that learns from data during training and estimate the predictive accuracy, so it generalizes well on the testing data. We can use probabilistic theory of Bayesian [
31] to develop a construct similar to direct table lookup. We assume a random variable to be ‘
rV’ that will appear with many values in set of
We will use prior probability
. Thus, we represent a class or set of classes as
and the greatest
, for given pattern of evidence (
pE) that classifier learns on
valid for all .
Therefore, we can write the conditional equation where
P (
pE) is considered with regard to probability of (
pE) is
valid for all . Finally, we can write the probability of the error for the above given pattern, as
P (
pE)
|error, assuming the cost function for all correct classification is 0, and for all incorrect is 1, then as stated earlier, the Bayesian classification will put the instance in the class labelling the highest posterior probability as
. Therefore, the construct can thus be determined as
. Let us construct the matrix function of all features, accepted and rejected features, based on GG and LG, as
Table 1 shows the various ranges for Minimum, Maximum and Middle points of the all three functions as discussed earlier.
Using Naïve Bayes multicategory equality as:
where
, and Fisher score algorithm [
3] can be used in FS to measure the relevance of each feature based on Laplacian score, such that
.
shows the no. of data samples in test class shown subscript ‘l’. Generally, we know that based on specific affinity matrix, .
To group the features based on relevancy score, we must ensure that each group member of the features exhibit low variance, medium stability and their score is based on optimum-fitness, thus each member follows
. This also ensure that we address the high dimensionality issue, as when feature appears in high dimension, they tend to change their value for training mode, thus, we determine the information gain using entropy function as:
V1 indicates the number of various value of the target features in set of
F. and
is the probability of the type of value of t in a complete subset of the feature tested. Similarly, we can calculate the entropy for each feature in
x,
y,
z dimension as:
Consequently, gain function in probability of entropy in 3D is determined as:
We develop a ratio of gain for each feature in z-dimension as this ensure the maximum fitness of the feature set for the given predictive modeling in the given dataset for which ML algorithm needs to be trained. Thus,
gR indicates the ratio between:
Figure 7 shows the displacement of the local gain and global gain functions based on probability distributions. As discussed earlier, LG and GG functions are developed to regulate the accuracy and thus validity of the classifier is measured initially based on accuracy metric.
Table 2 shows the probability of local and global error limits based on probability function (
Figure 7) in terms of local (g) and global gain function (G).
RULE 2If (g (err) < 0.2) Then
Flag ‘O.F’
Elseif (g (err) > 0.8) Flag ‘U.F’
If we assume the fact of
, such that
d (
and
d (
, where ‘
I’ is the global input of testing data. We also confirm the relevance of the feature in the set using objective Function construct in distribution ‘
d’, thus:
Then, Using Equations (14)–(17), we can finally get
Figure 8 Illustration of Feature Engineering and Feature Group as constructed in the mathematical model and governed by the Algorithms 1 and 2, defined later. Metrics API is available from eMLEE package. The white, yellow, and red orbital shapes indicate the local gain progression through 3D space. The little 3D shapes (
x,
y, and
z) in the accepted feature space in grouping indicates several (theoretically unlimited) instances of the optimized values as the quantization progresses.
Definition 5.
Feature selection is governed by satisfying the scoring function (score) in 3D space (x: Over-Fitness, y: Under-Fitness, z: Optimum-Fitness) for which evaluation criterion needs to be maximized, such that. There exist a weighted,function that quantifies the score for each feature, based on response from eMLEE engine with function, such that each feature in, has associated score for.
Two or more features may have the same predictive value and will be considered redundant. The non-linear relationship exists between two or more features (variables) that affects the stability and linearity of the learning process. If the incremental accuracy is improved, then non-linearity of a variable is ignored. As the number of the features are added or removed in the given set, the OF, UF, and B changes. Thus, we need to quantify their convergence, relevance, and covariance distribution across the space in 3D. We implement weighted function for each metric using LVQ technique [
1], in which, we measure each metric over several experimental runs for enhanced feature set, as reported back from the function explained in Theorems 1 and 2, such that we optimize the z-dimension for optimum fitness and reduce
x and
y dimension for over-fitness and under-fitness. Let us define:
where the piecewise effective decision border is
, In addition, the unit normal vector, (
) for border
is valid for all cases in space. Let us define the probability distribution of data on
Here, we can use the Parzen method [
32], to restore the nonparametric density estimation method, to estimate the
.
where
shows the Euclidean distance function.
Figure 9 shows the Euclidean distance function based on binary weights for
function.
Table 3 lists the quick comparison of the values of two functions as developed to observe the minimum and maximum bounds.
We used the Las Vegas Algorithm approach that helps to get correct solution at the end. We used it to validate the correctness of our gain function. This algorithm guarantees correct outcome if the solution is returned or created. It uses the probability approximate functions to implement runnable time-based instances. For our feature selection problem, we will have a set of features that will guarantee the optimum minimum set of features for acceptable classification accuracy. We use linear regression to compute the value of features to detect the non-linearity relationship between features, we thus implement a function,
. Where a, and b are two test features and values can be determined by using linear regression techniques, so
. Where,
,
,
. These equations also minimize the squared error. To compute weighted function, we use feature ranking technique [
12]. In this method, we will score each feature, based on quality measure such as information gain. Eventually, the large feature set will be reduced to a small feature set that is usable. The Feature Selection can be enhanced in several ways such as pre-processing, calculating information gain, error estimation, redundant feature or terms removal, and determining outlier’s quantification, etc. The information gain can be determined as:
‘
M’ shows the number of classes and ‘
P’ is the probability. ‘
W’ is the term that it contains as a feature.
is the conditional probability. In practice, the gain is normalized using Entropy, such as
Here we apply conventional variance-mean techniques. We can assume,
. The algorithm will ensure that ‘EC
’ stays in optimum bounds. Linear combination of Shannon information terms [
7] and conditional mutual information maximization (
CMIM) [
3] for
builds the functions as
By using Equations (23)–(27), we get
3.2. eFES Algorithms
The following algorithms aim: (i) to compute functions as raw feature extraction, related features identification, redundancy, and irrelevancy to prepare the layer for feature pre-processing; (ii) to compute and quantify the selection and grouping factor for the acceptance as model incorporates them; and (iii) to compute the optimization function of the model, based on weights and scoring functions. objeMLEE is the API call for accessing public functions
Following are the pre-requisites for the algorithms.
Initialization: Set the algorithm libraries, create subset of the dataset for random testing and then correlating (overlapping) tests.
Create: LTObject for
Create: ObjeMLEE (h)/*create an object reference of eMLEE API */
Set: ObjeMLEE.PublicFunctions (h.eABT,h.eFES,h.eWPM,h.eCVS)/* Handles for all four constructs*/
Global Input: ,
Dataset Selection: These algorithms require the dataset to be formatted and labelled with supervised learning in mind. These algorithms have been tested for miscellaneous datasets selected from different domains as listed in the
appendix. Some preliminary clean-up may be needed depending upon the sources and raw format of the data. For our model building, we developed a Microsoft SQL Server-based data warehouse. However raw data files such as TXT and CSV are valid input files.
Overall Goal (Big Picture): The foremost goal of these two algorithms is to govern the mathematical model built-in eFES unit. These algorithms are essential to work in a chronological mode, as the output of Algorithm 1 is required for Algorithm 2. The core idea that algorithms utilize is to quantify each feature either in original, revealed or an aggregated state. Based on such scoring, which is very dynamic and parallelized while classifier learning is being governed by these algorithms, the feature is removed, added, or put on the waiting list, for the second round of screening. This is the beauty of it. For example, Feature-X may be scored low in the first round and because Feature-Y is now added, that impacts the scoring of the Feature-X, and thus Feature-X is upgraded by scoring function and included accordingly. Finally, algorithms accomplish the optimum grouping of the features from the dataset. This scheme maximizes the relevance, reduces the redundancy, improves the fitness, accuracy, and generalization of the model for improved predictive modeling in any datasets.
Algorithm 1 aims to compute the low-level function as F.Prep (x, y, z), based on final Equations (26) and (27) as developed in the model earlier. It uses the conditions of Irrelevant feature and Redundant feature functions and run the logic if the values are below 50% as a check criterion. This algorithm splits the training data based on popular approach as cross validation. However, it must be noted in line 6, that we use our model API for improving the value of k in the process, that we call enhanced cross validation. LT object regulates it and optimizes the value of k based on the classifier performance in the real time. It then follows the error rule (80%, 20%) and keeps track of each corresponding feature, as they are added or removed. Finally, it gets to the start using the gain function in 3D space for each fitting factor since our model is based on 3D scoring of each feature in the space where point is moved in x, y, and z values in space (logical tracking during classifier learning).
Algorithm 2 aims to use the output of algorithm 1 in conjunction with computing many other crucial functions to compute a final function of feature grouping function (FGF). It uses the weighted function to analyze each participating feature including the ones that were rejected. It also utilizes the LT object and its internal functions using the API. This algorithm slices the data into various non-overlapping segments. It uses one segment at a time, then randomly mixed them for more slices to improve the classifier generalization ability during the training phase. It uses
as a LT object from the library of eMLEE and records the coordinates for each feature. This way, entry is made in LT class, corresponding to the gain function as shown in lines 6 to 19. From line 29 to 35, it also uses probability distribution function, as explained earlier. It computes two crucial functions of
and
. For this global gain (GG) function, each distribution of local gain
g (
x,
y,
z) must be considered as features come in for each test. All the low probability-based readings are discarded for active computation but kept in waiting list in the LT object for the second run. This way, algorithm does justice to each feature and give it a second chance before finally discarding it. The rest of the features that qualify in first or second run, are then added to the FGF.
Example 1. In one of the experiments (such as Figure 13) on dataset with features including ‘RELIGION’, we discovered something very interesting and intuitive. The data was based on survey from students, as listed in the appendix. We then formatted some of the sets from different regions and ran our Good Fit Student (GFS) and Good Fit job Candidate (GFjC) algorithms (as we briefly discuss in future works). GFS and GFjC are based on eMLEE model and utilize eFES. We noticed as a pleasant surprise that in some cases, it rejected the RELIGION feature for GFS prediction and this made sense as normally religion will not influence success in the studies of the student, but then we discovered that it gave some acceptable scoring to the same feature, because it was coming from a different GEOGRAPHICAL region of the world. It made sense as well, because religion’s influence on the individual may be diverse depending on his or her background. We noticed that it successfully correlated with Correlation Factor (CF) > 0.83 on other features in the set and considered the associated feature to be given high score due to being appeared with the other features of the collateral importance (i.e., Geographical information). CF is one of the crucial factors in GFS and GFjC algorithms. GFS and GFjC are out of the scope of this paper.
| Algorithm 1. Feature Preparation Function—F.Prep (x, y, z) |
![Applsci 08 00646 i001]() |
Another example was encountered where this feature played significant role in the job industry where a candidate’s progress can be impacted based on their religious background. Another example is of GENDER feature/attribute that we discuss in
Section 6.1. This also explains our motivation towards creating FGF (Algorithm 2).
FGF function determines the right number and type of the features from a given data set during classifier learning and reports accordingly if satisfactory accuracy and generalization have not been reached. eFES unit, as explained in the model earlier, uses 3D array to store the scoring via LT object in the inner layer of the model. Therefore, eFES algorithms can tell the model if more features are needed to finally train the classifier for acceptable prediction in the real-world test.
Some other examples are data from healthcare, where a health condition (a feature) may become of high relevance if a certain disease is being predicted. For example, to predict the likelihood of cancer in a patient, DIABETES can have higher predictive score, because an imbalanced sugar can feed the cancerous cells. During learning, the classifier function starts identification of the features and then start adding or removing them based on effectiveness of the cost and time. Compared to other approaches where such proactive quantification is not done the eFES scheme dominates.
| Algorithm 2. Feature Grouping Function (FGF) |
![Applsci 08 00646 i002]() |
Figure 10 simulations demonstrate the global gain and local gain functions coherences with respect to Loss and Cost functions.
Figure 10a shows that gain function is unstable when eFES randomly created the feature set.
Figure 10b shows that gain functions stabilize when eFES uses weighted function, as derived in the model.