Forecasting of Energy Consumption in China Based on Ensemble Empirical Mode Decomposition and Least Squares Support Vector Machine Optimized by Improved Shuffled Frog Leaping Algorithm
Abstract
:1. Introduction
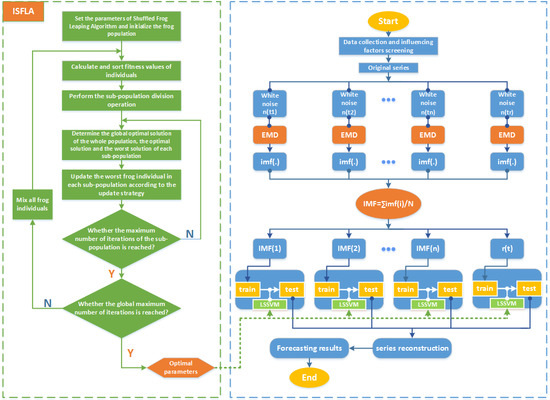
2. The Forecasting Model
2.1. Ensemble Empirical Mode Decomposition
2.1.1. Empirical Mode Decomposition (EMD)
- (1)
- The maximum difference between the number of extremes and the number of zero points is one;
- (2)
- The upper envelope and the lower envelope should be symmetrical.
- (1)
- Determine all maxima and minima of signal ;
- (2)
- According to the maximum and minimum of signal, construct the upper envelope and lower envelope of using three spline interpolation method;
- (3)
- Find the local average of the signal, ;
- (4)
- Calculate the difference between and , ;
- (5)
- Determine whether satisfies the conditions of IMF, and if the conditions are satisfied, the first IMF component can be obtained; otherwise, repeat the above steps until the signal meets the IMF conditions.
- (6)
- Define , and determine whether needs to be decomposed. If so, repeat the above steps by replacing with , otherwise end the decomposition.
2.1.2. Ensemble Empirical Mode Decomposition (EEMD)
- (1)
- Add random Gaussian white noise sequence to the signalwhere is the amplitude factor of added white noise; is the white noise sequence.
- (2)
- Decompose the signal into a group of intrinsic mode functions using Empirical Mode Decomposition with white noise;
- (3)
- Add a different white noise sequence each time, and then, repeat the steps of (1) and (2);
- (4)
- Calculate the mean value of decomposed IMFs, and take the average value of each IMF obtained by decomposition as the final result.where is the integration number using EMD; is the th IMF in the th decomposition.
2.2. Least Squares Support Vector Machine (LSSVM)
2.3. Improved Shuffled Frog Leaping Algorithm
2.3.1. Shuffled Frog Leaping Algorithm (SFLA)
- (1)
- Arranging the first frog in the first sub-population, the second frog in the second sub-population, the th frog in the th sub-population, and the th frog in the th sub-population, until all the frogs have been arranged into their sub-populations.
- (2)
- For each sub-population, fitness values of individuals are calculated. The frog with the best fitness is set as ; The frog with the worst fitness is set as ; The frogs with optimal fitness in the whole population is set as .
- (3)
- During each evolution of the sub-population, local search of is carried out to update the sub-population. The update strategy is as follows:where is a random value distributing between [0, 1]; is the largest step of frog.
- (4)
- If the fitness value of updated frog is better than that of the original frog , replace with . Otherwise, replace with . If the new solution obtained is still worse than the original frog , take a randomly generated new position to replace the original frog . Continue to repeat the above process until local search ends.
- (5)
- Re-divide the population and start local search again. Repeat the above steps until the algorithm meets the end condition.
2.3.2. Improved Shuffled Frog Leaping Algorithm (ISFLA)
2.4. Least Squares Support Vector Machine Optimized by Improved Shuffled Frog Leaping Algorithm
- (1)
- Set the Shuffled Frog Leaping Algorithm parameters and initialize the frog population;
- (2)
- Calculate the frog individuals’ fitness values and sort them;
- (3)
- Divide sub-populations and determine the global optimal solution of the whole population, the optimal solution and the worst solution of each sub-population;
- (4)
- Search and update the worst local frog individuals in each sub-population until the local search ends;
- (5)
- Mix the updated subgroups;
- (6)
- Determine whether the maximum iterative number is reached. If so, stop optimization and output the optimal solution. Otherwise, turn to Step (2);
- (7)
- Assign the optimized parameters to Least Squares Support Vector Machine for constructing the forecasting model.
2.5. The Forecasting Model Based on Ensemble Empirical Mode Decomposition and Least Squares Support Vector Machine Optimized by Improved Shuffled Frog Leaping Algorithm (EEMD-ISFLA-LSSVM)
3. Empirical Analysis
3.1. Influencing Factors Screening for Model Input
3.2. Forecasting of Energy Consumption in China Based on EEMD-ISFLA-LSSVM Model
3.3. Model Comparison and Error Analysis
3.4. Forecasting of Energy Consumption in China Based on the EEMD-ISFLA-LSSVM Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hsu, C.C.; Chen, C.Y. Applications of improved grey prediction model for power demand forecasting. Energy Convers. Manag. 2003, 44, 2241–2249. [Google Scholar] [CrossRef]
- Lin, C.S.; Liou, F.M.; Huang, C.P. Grey forecasting model for CO2 emissions: A Taiwan study. Adv. Mater. Res. 2011, 88, 3816–3820. [Google Scholar] [CrossRef]
- Lee, Y.S.; Tong, L.I. Forecasting energy consumption using a grey model improved by incorporating genetic programming. Energy Convers. Manag. 2011, 52, 147–152. [Google Scholar] [CrossRef]
- Acaroglu, O.; Ozdemir, L.; Asbury, B. A fuzzy logic model to predict specific energy requirement for TBM performance prediction. Tunn. Undergr. Space Technol. 2008, 23, 600–608. [Google Scholar] [CrossRef]
- Gokulachandran, J.; Mohandas, K. Application of Regression and Fuzzy Logic Method for Prediction of Tool Life. Proc. Eng. 2012, 38, 3900–3912. [Google Scholar] [CrossRef]
- Chen, S.X.; Gooi, H.B.; Wang, M.Q. Solar radiation forecast based on fuzzy logic and neural networks. Renew. Energy 2013, 60, 195–201. [Google Scholar] [CrossRef]
- Ismail, Z.; Yahaya, A.; Shabri, A. Forecasting Gold Prices Using Multiple Linear Regression Method. Am. J. Appl. Sci. 2009, 6, 1509–1514. [Google Scholar] [CrossRef]
- Sehgal, V.; Tiwari, M.K.; Chatterjee, C. Wavelet Bootstrap Multiple Linear Regression Based Hybrid Modeling for Daily River Discharge Forecasting. Water Resour. Manag. 2014, 28, 2793–2811. [Google Scholar] [CrossRef]
- Mu, H.; Dong, X.; Wang, W.; Ning, Y.; Zhou, W. Improved Gray Forecast Models for China’s Energy Consumption and CO, Emission. J. Desert Res. 2002, 22, 142–149. [Google Scholar]
- Lau, H.C.W.; Cheng, E.N.M.; Lee, C.K.M.; Ho, C.T.S. A fuzzy logic approach to forecast energy consumption change in a manufacturing system. Expert Syst. Appl. 2008, 34, 1813–1824. [Google Scholar] [CrossRef]
- Aranda, A.; Ferreira, G.; Mainar-Toledo, M.D.; Scarpellini, S.; Sastresa, E.L. Multiple regression models to predict the annual energy consumption in the Spanish banking sector. Energy Build. 2012, 49, 380–387. [Google Scholar] [CrossRef]
- Yang, J.F.; Cheng, H.Z. Application of SVM to power system short-term load forecast. Electr. Power Autom. Equip. 2004, 24, 30–32. [Google Scholar]
- Zhou, J.G.; Zhang, X.G. Projections about Chinese CO2 emissions based on rough sets and gray support vector machine. China Environ. Sci. 2013, 33, 2157–2163. [Google Scholar]
- Shi, X.; Huang, Q.; Chang, J.; Wang, Y.; Lei, J.; Zhao, J. Optimal parameters of the SVM for temperature prediction. Proc. Int. Assoc. Hydrol. Sci. 2015, 368, 162–167. [Google Scholar] [CrossRef]
- Hong, W.C. Electric load forecasting by support vector model. Appl. Math. Model. 2009, 33, 2444–2454. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Zheng, Y.H.; Li, L.X.; Zhou, L.D.; Sheng, X.K. Short-Term Wind Power Forecasting Based on Least-Square Support Vector Machine (LSSVM). Appl. Mech. Mater. 2013, 448, 1825–1828. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Malvoni, M.; Congedo, P.M. Comparison of strategies for multi-step ahead photovoltaic power forecasting models based on hybrid group method of data handling networks and least square support vector machine. Energy 2016, 107, 360–373. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, S.; Zhao, H. Energy-Related CO2 Emissions Forecasting Using an Improved LSSVM Model Optimized by Whale Optimization Algorithm. Energies 2017, 10, 874. [Google Scholar] [CrossRef]
- Sun, W.; He, Y.; Chang, H. Forecasting Fossil Fuel Energy Consumption for Power Generation Using QHSA-Based LSSVM Model. Energies 2015, 8, 939–959. [Google Scholar] [CrossRef]
- Ahmad, A.S.B.; Hassan, M.Y.B.; Majid, M.S.B. Application of hybrid GMDH and Least Square Support Vector Machine in energy consumption forecasting. In Proceedings of the IEEE International Conference on Power and Energy, Kota Kinabalu, Malaysia, 2–5 December 2012. [Google Scholar]
- Gutjahr, W.J. ACO algorithms with guaranteed convergence to the optimal solution. Inform. Process. Lett. 2002, 82, 145–153. [Google Scholar] [CrossRef]
- Liu, H.Y.; Jiang, Z.J. Research on Failure Prediction Technology Based on Time Series Analysis and ACO-LSSVM. Comput. Mod. 2013, 1, 219–222. [Google Scholar] [CrossRef]
- Ying, E. Network Safety Evaluation of Universities Based on Ant Colony Optimization Algorithm and Least Squares Support Vector Machine. J. Converg. Inf. Technol. 2012, 7, 419–427. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. A modified Artificial Bee Colony algorithm for real-parameter optimization. Inf. Sci. 2012, 192, 120–142. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.M.; Coelho, L.d.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Xu, D.Y.; Ding, S. Research on improved GWO-optimized SVM-based short-term load prediction for cloud computing. Comput. Eng. Appl. 2017, 53, 68–73. [Google Scholar]
- Long, W.; Liang, X.-M.; Long, Z.-Q.; Li, Z.-H. Parameters selection for LSSVM based on modified ant colony optimization in short-term load forecasting. J. Cent. South Univ. 2011, 42, 3408–3414. [Google Scholar]
- Yusof, Y.; Kamaruddin, S.S.; Husni, H.; Ku-Mahamud, K.R.; Mustaffa, Z. Forecasting Model Based on LSSVM and ABC for Natural Resource Commodity. Int. J. Comput. Theory Eng. 2013, 5, 906–909. [Google Scholar] [CrossRef]
- Mustaffa, Z.; Sulaiman, M.H.; Kahar, M.N.M. Training LSSVM with GWO for price forecasting. In Proceedings of the International Conference on Informatics, Electronics & Vision, Fukuoka, Japan, 15–18 June 2015. [Google Scholar]
- Pan, Q.K.; Wang, L.; Gao, L.; Li, J. An effective shuffled frog-leaping algorithm for lot-streaming flow shop scheduling problem. Int. J. Adv. Manuf. Technol. 2011, 52, 699–713. [Google Scholar] [CrossRef]
- Eusuff, M.; Lansey, K.; Pasha, F. Shuffled frog-leaping algorithm: A memetic meta-heuristic for discrete optimization. Eng. Optim. 2006, 38, 129–154. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, Q.; Jia, M. Improved shuffled frog leaping algorithm-based BP neural network and its application in bearing early fault diagnosis. Neural Comput. Appl. 2016, 27, 375–385. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, M.; Yu, Q.; Zhang, H. Comparing the application of EMD and EEMD on time-frequency analysis of seimic signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar] [CrossRef]
- Jiang, X.; Zhang, L.; Chen, X. Short-term forecasting of high-speed rail demand: A hybrid approach combining ensemble empirical mode decomposition and gray support vector machine with real-world applications in China. Transp. Res. C Emerg. Technol. 2014, 44, 110–127. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, W.; Zeng, J. A new short-term load forecasting method of power system based on EEMD and SS-PSO. Neural Comput. Appl. 2014, 24, 973–983. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E.; Chen, X. The Multi-Dimensional Ensemble Empirical Mode Decomposition Method. Adv. Adapt. Data Anal. 2009, 1, 339–372. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]














| Influencing Factor | Grey Relational Degree |
|---|---|
| population | 0.7781 |
| GDP | 0.8088 |
| industrial structure | 0.7624 |
| energy consumption structure | 0.7545 |
| energy intensity | 0.6568 |
| carbon emissions intensity | 0.6530 |
| total imports and exports | 0.8181 |
| Year | Actual Value (104 tce) | Forecasting Value (104 tce) | RE (%) |
|---|---|---|---|
| 1990 | 98,703 | 102,498 | 3.85 |
| 1991 | 103,783 | 101,262 | 2.43 |
| 1992 | 109,170 | 110,988 | 1.67 |
| 1993 | 115,993 | 115,923 | 0.06 |
| 1994 | 122,737 | 126,733 | 3.26 |
| 1995 | 131,176 | 134,031 | 2.18 |
| 1996 | 135,192 | 137,139 | 1.44 |
| 1997 | 135,909 | 130,536 | 3.95 |
| 1998 | 136,184 | 134,441 | 1.28 |
| 1999 | 140,569 | 140,805 | 0.17 |
| 2000 | 146,964 | 153,695 | 4.58 |
| 2001 | 155,547 | 162,075 | 4.20 |
| 2002 | 169,577 | 171,559 | 1.17 |
| 2003 | 197,083 | 195,744 | 0.68 |
| 2004 | 230,281 | 230,056 | 0.10 |
| 2005 | 261,369 | 260,912 | 0.17 |
| 2006 | 286,467 | 282,653 | 1.33 |
| 2007 | 311,442 | 308,834 | 0.84 |
| 2008 | 320,611 | 322,859 | 0.70 |
| 2009 | 336,126 | 334,721 | 0.42 |
| 2010 | 360,648 | 356,996 | 1.01 |
| 2011 | 387,043 | 383,739 | 0.85 |
| 2012 | 402,138 | 403,889 | 0.44 |
| 2013 | 416,913 | 415,380 | 0.37 |
| 2014 | 425,806 | 428,055 | 0.53 |
| 2015 | 429,905 | 432,790 | 0.67 |
| 2016 | 436,000 | 429,665 | 1.45 |
| Model | MAPE (%) | RMSE (107 tce) | MAE (107 tce) |
|---|---|---|---|
| EEMD-ISFLA-LSSVM | 1.47 | 3.27 | 2.72 |
| ISFLA-LSSVM | 3.16 | 8.46 | 7.04 |
| SFLA-LSSVM | 4.42 | 10.08 | 8.28 |
| LSSVM | 6.66 | 18.62 | 15.45 |
| BP | 7.68 | 19.68 | 15.94 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, S.; Niu, D.; Li, Y. Forecasting of Energy Consumption in China Based on Ensemble Empirical Mode Decomposition and Least Squares Support Vector Machine Optimized by Improved Shuffled Frog Leaping Algorithm. Appl. Sci. 2018, 8, 678. https://doi.org/10.3390/app8050678
Dai S, Niu D, Li Y. Forecasting of Energy Consumption in China Based on Ensemble Empirical Mode Decomposition and Least Squares Support Vector Machine Optimized by Improved Shuffled Frog Leaping Algorithm. Applied Sciences. 2018; 8(5):678. https://doi.org/10.3390/app8050678
Chicago/Turabian StyleDai, Shuyu, Dongxiao Niu, and Yan Li. 2018. "Forecasting of Energy Consumption in China Based on Ensemble Empirical Mode Decomposition and Least Squares Support Vector Machine Optimized by Improved Shuffled Frog Leaping Algorithm" Applied Sciences 8, no. 5: 678. https://doi.org/10.3390/app8050678
APA StyleDai, S., Niu, D., & Li, Y. (2018). Forecasting of Energy Consumption in China Based on Ensemble Empirical Mode Decomposition and Least Squares Support Vector Machine Optimized by Improved Shuffled Frog Leaping Algorithm. Applied Sciences, 8(5), 678. https://doi.org/10.3390/app8050678