Fault Detection in a Multistage Gearbox Based on a Hybrid Demodulation Method Using Modulation Intensity Distribution and Variational Mode Decomposition
Abstract
:1. Introduction
2. Theory of VMD
2.1. A Brief Introduction of the VMD Algorithm
2.2. Reduced Frequency Aliasing Effect
3. The Proposed Hybrid Demodulation Technique
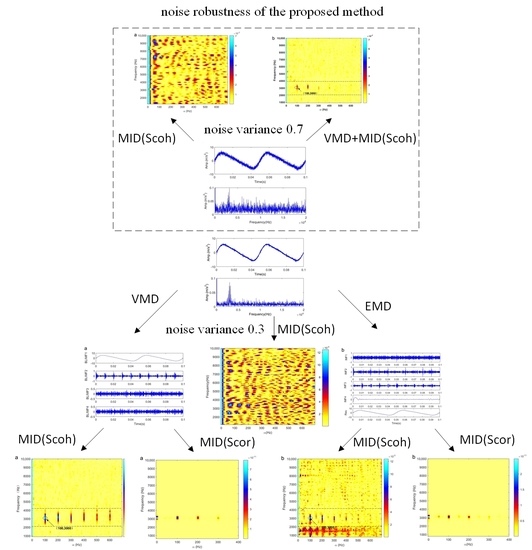
3.1. Modulation Intensity Distribution
3.2. A Hybrid Demodulation Technique via MID and VMD
4. Identification of a Tooth Defect Using the Proposed Technique
4.1. The Test Rig
4.2. Tooth Root Crack
4.3. Chipped Tooth
4.4. Tooth Surface Abrasion
4.5. Broken Tooth
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zhang, D.; Yu, D. Multi-fault diagnosis of gearbox based on resonance-based signal sparse decomposition and comb filter. Measurement 2017, 103, 361–369. [Google Scholar] [CrossRef]
- Li, Z.; Yan, X.; Yuan, C.; Peng, Z.; Li, L. Virtual prototype and experimental research on gear multi-fault diagnosis using wavelet-autoregressive model and principal component analysis method. Mech. Syst. Signal Process. 2011, 25, 2589–2607. [Google Scholar] [CrossRef]
- Jing, L.; Zhao, M.; Li, P.; Xu, X. A convolutional neural network based feature learning and fault diagnosis method for the condition monitoring of gearbox. Measurement 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Chen, J.; Patton, R.J. Robust Model-Based Fault Diagnosis for Dynamic Systems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Ding, S.X. Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms, and Tools; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Dalpiaz, G.; Rubini, R.; D’Elia, G.; Cocconcelli, M.; Chaari, F.; Zimroz, R.; Bartelmus, W.; Haddar, M. Advances in Condition Monitoring of Machinery in Non–Stationary Operations; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Feng, Z.; Zhang, D.; Zuo, M.J. Planetary gearbox fault diagnosis via joint amplitude and frequency demodulation analysis based on variational mode decomposition. Appl. Sci. 2017, 7, 775. [Google Scholar] [CrossRef]
- Nacib, L.; Saad, S.; Sakhara, S. A comparative study of various methods of gear faults diagnosis. J. Fail. Anal. Prev. 2014, 14, 645–656. [Google Scholar] [CrossRef]
- Fan, X.; Zuo, M.J. Gearbox fault detection using Hilbert and wavelet packet transform. Mech. Syst. Signal Process. 2006, 20, 966–982. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Zi, Y. Enhancement of signal denoising and multiple fault signatures detecting in rotating machinery using dual-tree complex wavelet transform. Mech. Syst. Signal Process. 2010, 24, 119–137. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R.; Xiang, J.; Zheng, W. Research on variational mode decomposition and its application in detecting rub impact fault of the rotor system. Mech. Syst. Signal Process. 2015, 60, 243–251. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R. Filter bank property of variational mode decomposition and its applications. Signal Process. 2016, 120, 509–521. [Google Scholar] [CrossRef]
- Mohanty, S.; Gupta, K.K.; Raju, K.S. Hurst based vibro-acoustic feature extraction of bearing using EMD and VMD. Measurement 2018, 117, 200–220. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; He, S.; Jiang, Z. Bearing fault diagnosis based on variational mode decomposition and total variation denoising. Meas. Sci. Technol. 2016, 27. [Google Scholar] [CrossRef]
- Urbanek, J.; Antoni, J.; Barszcz, T. Detection of signal component modulations using modulation intensity distribution. Mech. Syst. Signal Process. 2012, 28, 399–413. [Google Scholar] [CrossRef]
- Tian, X.; Gu, J.X.; Rehab, I.; Abdalla, G.M.; Gu, F.; Ball, A.D. A robust detector for rolling element bearing condition monitoring based on the modulation signal bispectrum and its performance evaluation against the Kurtogram. Mech. Syst. Signal Process. 2017, 100, 167–187. [Google Scholar] [CrossRef]
- Zhang, R.; Gu, X.; Gu, F.; Wang, T.; Ball, A.D. Gear Wear Process Monitoring Using a Sideband Estimator Based on Modulation Signal Bispectrum. Appl. Sci. 2017, 7, 274. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B. Simulating gear and bearing interactions in the presence of faults: Part I. The combined gear bearing dynamic model and the simulation of localised bearing faults. Mech. Syst. Signal Process. 2008, 22, 1924–1951. [Google Scholar] [CrossRef]
- Antoni, J. Cyclostationarity by examples. Mech. Syst. Signal Process. 2009, 23, 987–1036. [Google Scholar] [CrossRef]
- Staszewski, W.J.; Worden, K.; Tomlinson, G.R. Time–frequency analysis in gearbox fault detection using the Wigner–Ville distribution and pattern recognition. Mech. Syst. Signal Process. 1997, 11, 673–692. [Google Scholar] [CrossRef]
- Antoni, J. Cyclic spectral analysis of rolling-element bearing signals: Facts and fictions. J. Sound Vib. 2007, 304, 497–529. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J.; Chobsaard, S. The relationship between spectral correlation and envelope analysis in the diagnostics of bearing faults and other cyclostationary machine signals. Mech. Syst. Signal Process. 2001, 15, 945–962. [Google Scholar] [CrossRef]
- Liu, H.; Song, B.; Qin, H.; Qiu, Z. An adaptive-ADMM algorithm with support and signal value detection for compressed sensing. IEEE Signal Process. Lett. 2013, 20, 315–318. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E.; Chen, X. The multi-dimensional ensemble empirical mode decomposition method. Adv. Adapt. Data Anal. 2009, 1, 339–372. [Google Scholar] [CrossRef]
- Urbanek, J.; Barszcz, T.; Antoni, J. Integrated modulation intensity distribution as a practical tool for condition monitoring. Appl. Acoust. 2014, 77, 184–194. [Google Scholar] [CrossRef]
- Gardner, W. Measurement of spectral correlation. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 1111–1123. [Google Scholar] [CrossRef]
- Xiang, J.; Zhong, Y.; Gao, H. Rolling element bearing fault detection using PPCA and spectral kurtosis. Measurement 2015, 75, 180–191. [Google Scholar] [CrossRef]
- Urbanek, J.; Barszcz, T.; Sawalhi, N.; Randall, R. Comparison of amplitude-based and phase-based methods for speed tracking in application to wind turbines. Metrol. Meas. Syst. 2011, 18, 295–304. [Google Scholar] [CrossRef]
- Bartelmus, W.; Zimroz, R. A new feature for monitoring the condition of gearboxes in non-stationary operating conditions. Mech. Syst. Signal Process. 2009, 23, 1528–1534. [Google Scholar] [CrossRef]


























© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Wang, Y.; Yang, J.; Zhang, S. Fault Detection in a Multistage Gearbox Based on a Hybrid Demodulation Method Using Modulation Intensity Distribution and Variational Mode Decomposition. Appl. Sci. 2018, 8, 696. https://doi.org/10.3390/app8050696
Hu C, Wang Y, Yang J, Zhang S. Fault Detection in a Multistage Gearbox Based on a Hybrid Demodulation Method Using Modulation Intensity Distribution and Variational Mode Decomposition. Applied Sciences. 2018; 8(5):696. https://doi.org/10.3390/app8050696
Chicago/Turabian StyleHu, Chaofan, Yanxue Wang, Jianwei Yang, and Suofeng Zhang. 2018. "Fault Detection in a Multistage Gearbox Based on a Hybrid Demodulation Method Using Modulation Intensity Distribution and Variational Mode Decomposition" Applied Sciences 8, no. 5: 696. https://doi.org/10.3390/app8050696
APA StyleHu, C., Wang, Y., Yang, J., & Zhang, S. (2018). Fault Detection in a Multistage Gearbox Based on a Hybrid Demodulation Method Using Modulation Intensity Distribution and Variational Mode Decomposition. Applied Sciences, 8(5), 696. https://doi.org/10.3390/app8050696