Study on Path Planning Method for Imitating the Lane-Changing Operation of Excellent Drivers
Abstract
:1. Introduction
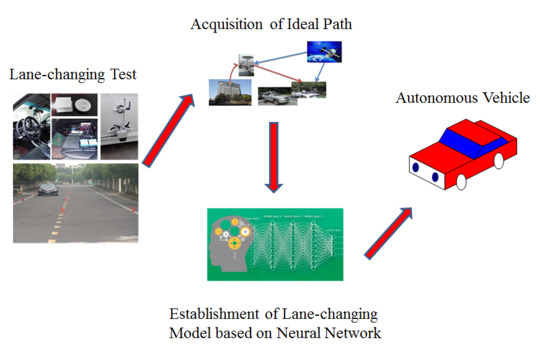
2. Acquisition of Ideal Path
2.1. Lane-Changing Test
2.2. Data Processing
3. Fitting of the Test Path
4. Path Planning Method Based on Excellent Driver Lane-Changing Model
4.1. GA-BP Neural Networks
4.2. Excellent Driver Lane-Changing Model
5. Simulation and Analysis
5.1. Obstacle Avoidance Simulation
5.2. Free Lane-Changing Simulation
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Rasekhipour, Y.; Khajepour, A.; Chen, S.K. A Potential Field-Based Model Predictive Path-Planning Controller for Autonomous Road Vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1255–1267. [Google Scholar] [CrossRef]
- Korayem, M.H.; Nekoo, S.R. The SDRE control of mobile base cooperative manipulators: Collision free path planning and moving obstacle avoidance. Robot. Auton. Syst. 2016, 86, 86–105. [Google Scholar] [CrossRef]
- Gao, Y.Q.; Gray, A.; Tseng, H.E. A tube-based robust nonlinear predictive control approach to semiautonomous ground vehicles. Veh. Syst. Dyn. 2014, 52, 802–823. [Google Scholar] [CrossRef]
- Gao, Y.Q.; Lin, T.; Borrelli, F. Predictive Control of Autonomous Ground Vehicles With Obstacle Avoidance on Slippery Roads. In Proceedings of the ASME 2010 Dynamic Systems and Control Conference, Cambridge, MA, USA, 12–15 September 2010; pp. 265–272. [Google Scholar]
- Donatelli, M.; Giannelli, C.; Mugnaini, D. Curvature continuous path planning and path finding based on PH splines with tension. Comput. Aided Des. 2017, 88, 14–30. [Google Scholar] [CrossRef]
- Giannelli, C.; Mugnaini, D.; Sestini, A. Path planning with obstacle avoidance by G1 PH quintic splines. Comput. Aided Des. 2016, 76, 47–60. [Google Scholar] [CrossRef]
- Choi, J.W.; Curry, R.E.; Elkaim, G.H. Curvature-continuous trajectory generation with corridor constraint for autonomous ground vehicles. In Proceedings of the 49th IEEE Conference on Decision and Control, Hilton Atlanta Hotel, Atlanta, GA, USA, 15–17 December 2010; pp. 7166–7171. [Google Scholar]
- Meyer, G.; Beiker, S. Road Vehicle Automation 2; Springer International Publishing: Cham, Switzerland, 2015; ISBN 978-3-319-19077-8. [Google Scholar]
- Elbanhawi, M.; Simic, M.; Jazar, R. Improved maneuvering of autonomous passenger vehicles: Simulations and field results. J. Vib. Control 2017, 23, 1954–1983. [Google Scholar] [CrossRef]
- Diels, C.; Bos, J.E. Self-driving carsickness. Appl. Ergon. 2016, 53, 374–382. [Google Scholar] [CrossRef] [PubMed]
- Cao, P.; Hu, Y.; Miwa, T. An optimal mandatory lane change decision model for autonomous vehicles in urban arterials. J. Intell. Transp. Syst. 2017, 21, 271–284. [Google Scholar] [CrossRef]
- Butakov, V.A.; Ioannou, P. Personalized driver/vehicle lane change models for ADAS. IEEE Trans. Veh. Technol. 2015, 64, 4422–4431. [Google Scholar] [CrossRef]
- Nilsson, J.; Brännström, M.; Coelingh, E. Lane change maneuvers for automated vehicles. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1087–1096. [Google Scholar] [CrossRef]
- Nilsson, J.; Brannstrom, M.; Coelingh, E. Longitudinal and lateral control for automated lane change maneuvers. In Proceedings of the American Control Conference, Palmer House Hilton, Chicago, IL, USA, 1–3 July 2015; pp. 1399–1404. [Google Scholar]
- Dubins, L.E. On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Lamiraux, F.; Lammond, J.P. Smooth motion planning for car-like vehicles. IEEE Trans. Robot. Autom. 2001, 17, 498–501. [Google Scholar] [CrossRef]
- Choi, Y.G.; Lim, K.I.; Kim, J.H. Lane change and path planning of autonomous vehicles using GIS. In Proceedings of the 12th International Conference on Ubiquitous Robots and Ambient Intelligence, KINTEX, Goyang, Korea, 28–30 October 2015; pp. 163–166. [Google Scholar]
- Ren, D.B.; Zhang, J.Y.; Zhang, J.M. Trajectory planning and yaw rate tracking control for lane changing of intelligent vehicle on curved road. Sci. China Technol. Sc. 2011, 54, 630–642. [Google Scholar] [CrossRef]
- Wang, C.; Zheng, C.Q. Lane change trajectory planning and simulation for intelligent vehicle. Adv. Mater. Res. 2013, 671, 2843–2846. [Google Scholar] [CrossRef]
- Yang, T.; Asanjan, A.A.; Faridzad, M. An enhanced artificial neural network with a shuffled complex evolutionary global optimization with principal component analysis. Inf. Sci. 2017, 418, 302–316. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Yin, F.; Zhang, Y.M. Drawing and recognizing Chinese characters with recurrent neural network. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 99, 849–862. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Saon, G.; Soltau, H.; Nahamoo, D. Speaker adaptation of neural network acoustic models using i-vectors. In Proceedings of the IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU), Olomouc, Czech Republic, 8–13 December 2013; pp. 55–59. [Google Scholar]
- Li, J.C.; Zhao, D.L.; Ge, B.F. A link prediction method for heterogeneous networks based on BP neural network. Physics A 2017, 495, 1–17. [Google Scholar] [CrossRef]
- Sharifian, A.; Ghadi, M.J.; Ghavidel, S. A new method based on Type-2 fuzzy neural network for accurate wind power forecasting under uncertain data. Renew. Energy 2018, 120, 220–230. [Google Scholar] [CrossRef]
- Xue, H.; Bai, Y.; Hu, H. Influenza activity surveillance based on multiple regression model and artificial neural network. IEEE Access. 2018, 6, 563–575. [Google Scholar] [CrossRef]
- Al-Qutami, T.A.; Ibrahim, R.; Ismail, I. Virtual multiphase flow metering using diverse neural network ensemble and adaptive simulated annealing. Expert Syst. Appl. 2018, 93, 72–85. [Google Scholar] [CrossRef]
- Yu, F.; Xu, X.Z. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network. Appl. Energy 2014, 134, 102–113. [Google Scholar] [CrossRef]
- Wang, S.X.; Zhang, N.; Wu, L. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Bin, W.; Zhu, X.; Shen, J. Analysis of driver emergency steering lane changing behavior based on naturalistic driving data. J. Tongji Univ. 2017, 45, 554–561. [Google Scholar]




















| Driver Number | Gender | Age | Driving Age (Years) |
|---|---|---|---|
| Driver 1 | Female | 55 | 33 |
| Driver 2 | Male | 28 | 10 |
| Driver 3 | Male | 53 | 31 |
| Driver 4 | Male | 46 | 22 |
| Driver 5 | Male | 53 | 21 |
| Classification | Information |
|---|---|
| Number of drivers | 5 |
| Velocity (km/h) | 30, 35, 40, 45, 50 |
| Distance from obstacle (m) | 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 100 (no obstacle) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, G.; Wu, Z.; Jiang, H.; Sun, L.; Duan, C. Study on Path Planning Method for Imitating the Lane-Changing Operation of Excellent Drivers. Appl. Sci. 2018, 8, 814. https://doi.org/10.3390/app8050814
Geng G, Wu Z, Jiang H, Sun L, Duan C. Study on Path Planning Method for Imitating the Lane-Changing Operation of Excellent Drivers. Applied Sciences. 2018; 8(5):814. https://doi.org/10.3390/app8050814
Chicago/Turabian StyleGeng, Guoqing, Zhen Wu, Haobin Jiang, Liqin Sun, and Chen Duan. 2018. "Study on Path Planning Method for Imitating the Lane-Changing Operation of Excellent Drivers" Applied Sciences 8, no. 5: 814. https://doi.org/10.3390/app8050814
APA StyleGeng, G., Wu, Z., Jiang, H., Sun, L., & Duan, C. (2018). Study on Path Planning Method for Imitating the Lane-Changing Operation of Excellent Drivers. Applied Sciences, 8(5), 814. https://doi.org/10.3390/app8050814