Next Article in Journal
Estimation of the Longitudinal Elasticity Modulus of Braided Synthetic Fiber Rope Utilizing Classical Laminate Theory with the Unit N/tex
Next Article in Special Issue
An Experimental Study on Dynamic Mechanical Properties of Fiber-Reinforced Concrete under Different Strain Rates
Previous Article in Journal
Modeling Properties with Artificial Neural Networks and Multilinear Least-Squares Regression: Advantages and Drawbacks of the Two Methods
Previous Article in Special Issue
Analysis and Modelling of Shrinkage and Creep of Reactive Powder Concrete
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 8
Issue 7
10.3390/app8071095
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Can We Truly Predict the Compressive Strength of Concrete without Knowing the Properties of Aggregates?

by
Jorge De Brito
1,*,
Rawaz Kurda
1 and
Pedro Raposeiro da Silva
2
1
Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais, 1049-001 Lisbon, Portugal
2
Instituto Superior de Engenharia de Lisboa, R. Conselheiro Emídio Navarro, 1950-062 Lisbon, Portugal
*
Author to whom correspondence should be addressed.
Appl. Sci. 2018, 8(7), 1095; https://doi.org/10.3390/app8071095
Submission received: 29 May 2018 / Revised: 13 June 2018 / Accepted: 29 June 2018 / Published: 5 July 2018
(This article belongs to the Special Issue New Trends in Recycled Aggregate Concrete)
Browse Figures
Versions Notes

Abstract

:
This paper is focused on the influence of the geological nature and quality of the aggregates on the compressive strength of concrete and explains why it is important not to ignore the characteristics of aggregates in the estimation of the strength of concrete, even for virgin aggregates. For this purpose, three original (Abrams, American Concrete Institute Manual of concrete practice and Slater) and two modified (Bolomey and Feret) models were used to calculate the strength of concrete by considering results of various publications. The results show that the models do not properly predict the strength of concrete when the characteristics of aggregates are neglected. The scatter between the calculated and experimental compressive strength of concrete, even when made with natural aggregates (NAs) only, was significant. For the same mix composition (with similar cement paste quality), there was a significant difference between the results when NAs of various geological nature (e.g., limestone, basalt, granite, sandstone) were used in concrete. The same was true when different qualities (namely in terms of density, water absorption and Los Angles abrasion) of aggregates were used. The scatters significantly decreased when the mixes were classified based on the geological nature of the aggregates. The same occurred when the mixes were classified based on their quality. For both modified models, the calculated strength of mixes made with basalt was higher than that of the mixes containing other types of the aggregates, followed by mixes containing limestone, quartz and granite. In terms of the quality of the aggregates, the calculated strength of concrete increased (was overestimated) as the quality of the aggregates decreased. The influence of the aggregates on the compressive strength of concrete became much more discernible when recycled aggregates were used mainly due to their more heterogeneous characteristics.

Graphical Abstract

1. Introduction

1.1. General Facts on Compressive Strength Estimation

Concrete is one of the most consumed materials in the construction industry. Apart from durability, consumers normally demand a target strength. The target strength can be achieved in different ways, e.g., by increasing the cement content, incorporating a specific amount of supplementary cementitious materials (SCM), and decreasing the water content or introducing a superplasticizer (SP). For that purpose, researchers have proposed several formulas to calculate the strength of concrete [1,2].
Researchers normally focus on the quality of the cement paste to calculate the strength of concrete. However, the strength of concrete not only depends on the strength of the hydrated product and the porosity of the cement paste [3] but also on the properties of the aggregates [4]. Further details regarding the mentioned factors are provided in the following paragraphs.
The strength of the hydrated product in the cement paste depends on the chemical and physical properties of cement [5,6]. The porosity of concrete depends on the air content that is mainly affected by the maximum size of the aggregates, and the particle size distribution in the used materials, mixing procedure, workability, placing, and compaction [4].
The properties of the aggregates directly or indirectly affect the strength of concrete. The influence of the aggregates’ properties can be clearly seen in high strength concrete, because failure occurs through the aggregates. For that purpose, a previous study [7] attempted to classify aggregates into four classes (A, B, C, and D) based on their physical properties, mainly by considering their density and water absorption (WA), and mechanical properties (Los Angeles (LA) abrasion) from the results of 116 studies (Table 1). The authors believe the strength of concrete produced with class A (high quality of aggregates) should be higher than that of those with B class, followed by classes C and D.
In our study, the strength of concrete made with ordinary Portland cement (OPC) and natural aggregates (NA) was calculated using different formulas (Section 1.2) and compared with the actual (experimental) strength. Then, the strength of the NA concrete was classified based on the quality of the aggregates. The first objective of this procedure was to show the importance of the quality of the aggregates rather than their procurement source (e.g., recycled aggregates (RA) versus NA) and confirm the relationship between the strength of concrete and the properties of the aggregates, regardless of the type of virgin aggregates used.
Regarding the indirect effects of the aggregates, studies have concluded that the quality of the hydration products affects the bond between the aggregates and cement paste (Interfacial Transition Zone—ITZ) [8]. Therefore, some of the recent investigations (Section 1.2) have considered the cement content and strength class of cement to calculate the strength of concrete. However, other studies [9] that updated the Bolomey formula [10] realized that, for the same quality of cement paste, the compressive strength of concrete made with rolled natural aggregates (NA) differs from that of concrete made with crushed NA, when both come from the same natural sources. This is because the shape of aggregates also affects the ITZ [11].
In fact, for concrete made with crushed aggregates, the effective water/cement ratio (main contributor to the quality of the cement paste and of the ITZ) should be increased in order to obtain the same workability as concrete made with rolled aggregates [12]. However, all the formulas proposed until then to calculate the strength of concrete failed to consider one of the most effective factors that affects the bond between aggregates and cement paste (ITZ), which is the texture of aggregates. The texture of the aggregates depends on the geological nature of the aggregates (e.g., limestone, basalt, sandstone, granite). For example, basalt can be considered to be a high-quality aggregate due to its high density and high mechanical strength, but its bond with the cement paste may be not strong enough due to its very smooth texture which is relatively similar to that of glass [11]. Thus, the calculated strength may be overestimated. In terms of chemical reactivity, the study of Kong and Du [11] showed that the amount of OH− that is absorbed by the aggregates and that releases Si4+ at the same time depends on the geological nature of the aggregates, and this process significantly affects the pore structure of the hydration product and the ITZ as a result.
Therefore, this study attempted to show the effect of the geological nature of the aggregates on the ultimate strength of concrete and how the scatter between the estimated and the actual strength of concrete decreases if the results take the geological nature of the virgin aggregates into account.
Generally, the geological nature of aggregates affects the ultimate strength of concrete in different ways. When the strength of aggregates is lower than that of the cement paste, the quality of the aggregates controls the ultimate strength, because failure occurs though the aggregates. However, when the strength of the aggregates is higher than that of the cement paste, failure may not only occur in the cement paste itself but also in the ITZ between the aggregates and the cement paste [13]. In fact, the quality of the aggregates needs to be considered a main factor in the estimation of the compressive strength for low and high strength concrete mixes. It is well known that failure normally occurs in the ITZ between the aggregates and the cement paste because the effective water to cement ratio (w/c) of the cement paste around the aggregate particles is higher than that of the other parts of the cement paste [14]. This phenomenon relates to the capillary absorption between cement paste and aggregates which is affected by the WA and density of the aggregates.
Since the effect of SP, binder content and its characteristics, the w/c and aggregate content and the parameters described in [15,16] on concrete have already been studied, this study focuses on the effects of the quality and geological nature of NA on the compressive strength of concrete when all the mentioned parameters are constant, mainly by considering two modified models shown in the next sub-section. Thus, in terms of the aggregates, it is advisable to focus on the two mentioned parameters rather than only on the source of the aggregates, e.g., NA versus RA. To that purpose, this study considered the results of 84 publications for concrete made with virgin aggregates and 41 other publications (Section 2) for concrete made with RA.

1.2. Background of the Compressive Strength Estimation Models

Feret [1] is considered one of the pioneers in devising a formula to calculate the strength of concrete based on the volume of aggregates to the cement ratio and the void index. He was followed by Abrams [2] who calculated the strength of concrete by taking into account the w/c ratio. A study of Hicks [17] simplified Slater’s formula [18] and reported that the strength of concrete linearly changes with the w/c ratio. Similarly to Slater’s formula, ACI 2000-I [19] calculated the strength of concrete by considering the effect of the w/c ratio.
Powers and Brownyard [3] concluded that the porosity of the cement paste affects the strength of concrete. Thus, they developed the Feret’s formula by considering another factor, namely, the “gel (volume of hydration products) to space (capillary porosity)” ratio. Then, Karni [20] added another factor (degree of hydration) to the Powers and Brownyard’s formula. Regarding the porosity of the cement paste, Popovics [21] introduced the influence of air content into Bolomey’s formula. Thirteen years afterwards, the same researcher [22] worked on Abrams’s formula and added the effects of cement’s hardening rate and the air content. Since the compressive strength of concrete with the same w/c may vary with its cement content, Popovics [23] then added another factor (cement content) to Abrams’s formula. However, the number of concrete samples considered to calibrate these factors and the new model were not significant compared to the previous model. Furthermore, de Larrard [13] updated Feret’s formula by considering the maximum paste thickness, the maximum size of the aggregates, the aggregates’ packing density, the content of pozzolanic binders and a few types of aggregates. However, de Larrard did not consider the properties of cement, and the number of concrete samples used to calculate the factors was not significant. A recent study [15] proposed an innovative way to calculate the strength of concrete mixes using the M5P model tree algorithm by taking into account the results of nine publications. However, the cement class (e.g., CEM I 35.5 or 42.5) and quality of the aggregates were not considered as main factors in the model.
According to the parameters considered in each of the models suggested by the above researchers, two common facts can be seen. First, some of the formulas calculate the strength of concrete by only taking into account the w/c ratio. However, it is well known that the strength of two concrete mixes with the same w/c may not be equal when their cement contents are different [23]. Therefore, the volume of aggregates to cement ratio and void index (water and air), which depend on the maximum size of the aggregates and the water content, should be considered. Secondly, most formulas fail to consider the strength class of cement. For example, the strength of concrete mixes made with the same cement content is not similar when different cement classes (e.g., CEM I 32.5 or 42.5) are used [24].
The majority of current formulas follow those of Feret [1] and Abrams [2]. In the past decades, a few researchers have attempted to update the mentioned formulas, but their results are still not reliable, since they only considered a few case studies (concrete samples) to calibrate the correction factors. However, Sika-comp recently released a new software (SIKA-mix design) to design concrete mixes by using Faury’s [25] method and calculate the strength of concrete by updating Feret’s [1] formula. Thus, the new Feret-based formula depends on the ratio of the volume of aggregates to cement, the void index, the strength class of cement (cement class), and the maximum size of aggregates. In addition, a study [9] proposed a modification of Bolomey’s [10] formula by taking into account the w/c ratio, the strength class of cement and the aggregates’ production method (e.g., crushed or natural). Thus, the two updated formulas (Feret and Bolomey) were used as the main models to analyse the results.

2. Methodology

Three original models (Abrams, Slater and ACI) (Table 2) and two modified models (Bolomey and Feret) (Table 2 and Table 3) were used to estimate the compressive strength at 28 days of concrete made with ordinary Portland cement (OPC) and NA. The mentioned formulas were applied to 206 concrete mixes (206 concrete mixes × minimum 3 samples = 618 concrete samples) made with 100% NA sourced from 84 studies (Table 4). After that, the results were classified based on the aggregates’ classes (Table 1) proposed by Silva et al. [7]. Then, the geological nature of the aggregates (e.g., limestone, basalt, granite, sandstone) was considered to analyse the results.
Additionally, for each analysis (by considering the aggregates’ quality or geological nature), different studies (Table 4) were considered based on the supplementary information given in the publication. For example, the studies that did not provide the geological nature of the aggregates (Table 4—5th row) were still considered in the analysis of the effect of the quality of the aggregates on the compressive strength of concrete when their WAs and densities were provided. In the first stage of this analysis, all the concrete mixes used were made with NA and OPC (without any SCM). In the second stage, some examples (Table 4) containing 100% coarse RA were studied.
It is well known that the shapes and sizes of the concrete samples (e.g., cube or cylinder) affect the results. Therefore, this study took into account these two factors, and the experimental results (non-standard cylinder sizes) were converted to be equivalent to those of a cylinder with a 150 mm diameter × 300 mm length (fcm, cube 100 mm → fcm, cube 150 mm → fcm, cylinder 150 × 300 ← fcm, cylinder 100 × 200) in order to compare them with the calculated strength. Thus, according to the state-of-the-art method described in FIB Bulletin 42 [118], the “fcm, cube 150 mm to fcm, cube 100 mm” ratio is equal to 0.97. Similar results can be seen in other studies [119,120]. After that, fcm, cube 150 mm was converted to fcm, cylinder 150 × 300, according to EN 1992-1-1:2004 (E). Regarding fcm, cylinder 100 × 200, the majority of the researchers agree that, up to 33 MPa, the difference between fcm, cylinder 150 × 300 and fcm, cylinder 100 × 200 is insignificant. The average difference between them is 2%, according to previous studies [121,122,123]. For higher strength values (over 33 MPa), the average “fcm, cylinder 150 × 300 to fcm, cylinder 100 × 200” ratio is 0.90 (Table 5).
As mentioned above, in this study, the strength of concrete made with OPC and NA was calculated using different formulas (Table 2) and compared with the actual (experimental) strength. Then, the strength of the NA concrete was classified based on the quality of the aggregates. The first objective of this procedure was to show the importance of the quality of the aggregates rather than their procurement source (e.g., recycled aggregates (RA) versus NA) and to confirm the relationship between the strength of concrete and the properties of the aggregates, regardless of the type of virgin aggregates used.

3. Results

Cement has been used as a construction material for many centuries. However, modern cement has been produced only in the last century. Due to the substantial changes made in cement production during the last decades, the quality of cement has significantly improved [128,129]. Therefore, the results of this study focus on the investigations published in the last two decades. Figure 1 shows the relationship between compressive strength and the w/c of concrete mixes made with only NA and OPC. The results show that, for a 95% confidence interval, there is a large amount of scatter between w/c and the compressive strength of concrete. This result was expected due to the quality of cement paste and aggregates. The effect of the quality of the cement paste on concrete strength has been extensively studied for decades, and several formulas have been suggested to relate these two properties. However, the effect of the quality of the aggregates on concrete strength had not previously been sufficiently studied. For this reason, this study focused on the effects of the physical and geological nature of the aggregates in the following sections.

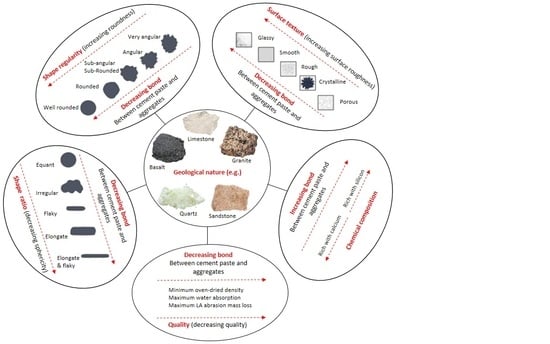
3.1. Effect of the Geological Nature of Natural Aggregates on the Compressive Strength of Concrete

As mentioned in the literature review, the strength of concrete may be affected by different factors, including the quality of the cement paste. Therefore, the original models (Abrams, Slater, and ACI) calculated the strength of concrete based on the w/c (Figure 2). The results showed that the estimated strength of concrete based on the quality of the cement paste is not accurate, and the relationship between the actual and calculated strength in all of the original models was poor (R2 was −0.31, −0.14 and 0.15 in the Abrams, Slater, and ACI models, respectively) when only w/c was considered to be an influencing factor. This is because the compressive strength of concretes with the same w/c may vary with cement content [23] and cement class [24], which respectively influence the aggregate: cement volume ratio and void index and the quality of the hydration product. The other reason is that the original formulas ignore the quality (e.g., geological nature) of the aggregates. Thus, the relationship between the calculated and actual strength of concrete mixes improved when the original formulas also considered the geological nature of the aggregates (R2 was −0.23, 0.03, −0.58, −0.05, 0.52 and 0.46 with Abram’s model, and 0.27, 0.20, −0.57, 0.20, 0.85 and 0 with Slater’s model, and 0.25, 0.40, −0.03, 0.23, 0.81, 0.84 with the ACI model when the aggregates were classified as basalt, granite, limestone, NA (geological nature not given), quartz, and sandstone, respectively. The negative R2 is due to the fact that the linear trendline was set to intercept the origin of the axes [130,131]). This behaviour is further discussed in the next paragraphs. Furthermore, for the 95% confidence intervals (red dashed lines in each graph), there is a big scatter between w/c and compressive strength of concrete, and the lower and upper k (fcm, calculated/fcm, experimental) values in all original models were 0.67 ± 0.02 and 1.67 ± 0.01, respectively.
As mentioned previously, the calculated strength based only on the w/c independently of the cement content and its properties, is not reliable. Therefore, this study essentially focused on the modified models (Bolomey and Feret) rather than the original models (Abrams, Slater, and ACI).
Figure 3a,b show the relationship between the experimental and calculated compressive strength obtained according to the Bolomey and Feret models, respectively. Relative to the original models (R2 was up 0.15) that only considered the w/c as a main factor, the relationship between the calculated and actual compressive strength significantly improved (R2 ≈ 0.50), as seen in Figure 3a. This is due to the additional factors considered in Bolomey’s model, namely the strength class of cement and the way that aggregates are produced (Table 2). However, this model neglected the effect of the cement content (volume of aggregates to cement ratio) which significantly affects the results due to its influence on the strength of concrete (for the same w/c, the strength may vary with the cement content [23]). As shown in Figure 3b, by using Feret’s model, the relationship between the calculated and experimental strength of concrete significantly improved (R2 ≈ 0.60) relative to the original models. This is because of the factors considered in the model, namely, the cement strength and content. However, this model neglected the aggregates’ production methods.
Even though the relationship between the actual and calculated strength improved by using the modified models (Bolomey and Feret), there was still a big scatter between the mixes (Figure 3). For example, for a 95% confidence interval, the k value (fcm, calculated/fcm, experimental) varied between 1.20–0.60 and 1.63–0.83 when the strength was calculated based on the Bolomey and Feret models, respectively. This may be related to the fact that both models neglected the properties of the aggregates as a factor to calculate the strength. To validate this assumption, the mixes were classified according to the geological nature of their aggregates, and the k value was found for each of them according to a 95% confidence interval (Figure 4). As a consequence, the relationship between calculated and actual strengths considerably improved in most cases. For example, the R2 of concrete mixes made with basalt, granite, limestone, and quartz was about 0.60, 0.80, 0.40, and 0.80 when Bolomey’s model was used to calculate the strength, and 0.40, 0.90, 0.60, 0.90 for Feret’s model, respectively. Additionally, for both the Bolomey (Figure 4a) and Feret models (Figure 4b), the difference between upper (k1) and lower (k2) boundaries (k value = fcm, calculated/fcm, experimental) for a 95% confidence interval of the concrete mixes significantly decreased when the classification was based on the geological nature of the aggregates, except for concrete with limestone aggregates. This is because limestone has a large scatter of characteristics (Table 4), and it is classified in various generic categories, e.g., carboniferous, dolomitic, and calcareous, or it may be a composite (e.g., limestone–quartzitic, limestone–siliceous).
In order to simplify the results, the average of the k1 and k2 values (as seen in Figure 4) was considered to make Figure 5. According to both models, all other parameters being the same, the calculated/actual strength ratio of concrete mixes made with basalt was higher than that of mixes containing other types of the aggregates, followed by mixes containing limestone, quartz, and granite. This ranking, which was repeated for both models, is further explained in the following paragraphs. Furthermore, apart from the above factors, the shape ratio and shape regularity of the aggregates may also affect the strength of concrete. For example, less water content (one of the main contributors to the quality of the cement paste and ITZ) is required to obtain the target slump with rolled aggregates compared to that with angular aggregates [12]. However, the bond between angular aggregates and cement paste is stronger than that in the mixes made with rolled aggregates. However, the bond also depends on the surface texture of the aggregates.
Ingham et al. [132] studied the shape, form, and texture of various geological natures of aggregates using about 270 cases. Based on their explanations and the classification of Silva et al. [7] (Section 1), Figure 6 was drawn to show all of the factors that may affect the influence of the aggregate on the quality of concrete. The shape ratio and shape regularity of the aggregates also affects the quality of concrete, but they can be controlled by sieving the aggregates. However, the surface texture of the aggregates and their quality and chemical composition may not be easily controlled. Therefore, it is important to identify the geological nature of the aggregates, because it determines the texture [132] and chemical composition [11], and in most cases, the physical characteristics, shape ratio, and regularity.
Notwithstanding a significant standard deviation that may be affected by the selected database, in both models, the calculated/actual strength ratio of concrete containing basalt was generally higher than that of the other aggregates (Figure 5). This is because, generally, basalt has an aphanitic texture or, in some cases, can be considered to be glassy [133]. As a consequence, the bond between basalt aggregates and cement paste will be weaker and failure may occur at ITZ. In other words, the models that calculate strength based on the quality of cement paste (without considering the geological nature of the aggregates) may fail, and relative to mixes containing other aggregates, the strength is overestimated. Furthermore, the chemical composition of the aggregates (rich with silicon or calcium), which influences the way they absorb other elements from the cement paste (and vice-versa), may also affect the interfacial hydrates around the aggregates. For example, limestone is rich in calcium, and therefore, there is more ettringite and calcium–hydroxide in the ITZ, while for basalt, which is rich in silicon, further calcium silicate hydrates are generated in that zone [11].
Unlike basalt aggregates, granites generally have a phaneritic texture [133]. This explains the trends shown in Figure 5, where the calculated/actual strength ratio of concrete containing granite is lower than that of the mixes made with other aggregates. The rougher surface of the granite increases the bond between cement paste and aggregates. Although both basalt and granite have similar chemical compositions (rich in silicon content) because of their surface texture, the ultimate strength of concrete with each aggregate and the same cement paste is different. Furthermore, the surface texture of the aggregates, as well as their chemical composition, shape ratio and regularity, and quality (e.g., WA and density) also affect the ultimate strength of concrete, as discussed in the following sections.

3.2. Effect of the Quality of Natural Aggregates on the Compressive Strength of Concrete

Concrete mixes were classified based on the aggregates’ quality, namely their WA, density, and LA abrasion (Table 1), according to the study by Silva et al. [7]. As for the geological nature (Section 3.1), the results show that the relationship between the calculated and actual strength of concrete (without taking into account the aggregates’ classes, the R2 values for the linear trends were 0.50 and 0.60 for the Bolomey and Feret formulas, respectively) improved when the mixes were classified based on their quality (classes A, B, C, and D). Thus, the R2 values for the linear trends were 0.72 and 0.62 for the Bolomey model and 0.60 and 0.74 for the Feret model when the mix’s aggregates were from classes AI and AII (specified in Table 1), respectively (Figure 7). This shows that the quality of the aggregates may significantly affect the ultimate strength of concrete. Therefore, it is important to identify the quality of the aggregates simultaneously with the other factors shown in Figure 6. According to both models, the scatter between the results (the k values of the all mixes were 0.6–1.30 and 0.80–1.50 when the strength was calculated according to the Bolomey and Feret models, respectively) decreases when the mixes are classified in terms of the quality of their aggregates (Figure 7).
In order to simplify the results, the average of the k1 and k2 values (as seen in Figure 7) was considered to make Figure 8. According to both models, all other parameters being the same, the calculated/actual strength ratio of concrete increases as the quality of the aggregates (high WA and LA abrasion, and low density “Table 1”) decreases. In low-strength concrete, failure normally happens at the ITZ. Apart from the factors discussed in Section 3.1, namely, the shape ratio and regularity, and the surface texture and chemical composition of the aggregates, this can be related to the fact that the w/c of the cement paste around the aggregates is higher than in other parts of the cement paste [14]. The quality of the aggregates, namely their WA and density, which both affect the capillary absorption between the aggregates and the cement paste, is a determinant of the ITZ bond strength. For high strength concrete, failure may not happen in the cement paste (the mechanical properties of the aggregates control concrete’s ultimate strength). Therefore, again, the quality of the aggregates, namely their LA abrasion, controls the ultimate strength of concrete. Additionally, relative to the Feret model, the calculated strength using Bolomey’s model is either close to the line of equality or below it. This may be related to the aggregates’ production method (rolled or crushed) considered in the formula, which helps to prevent overestimation of the compressive strength of the aggregates. This result also proves the importance of considering the properties of aggregates to calculate the strength of concrete.
In order to further show the importance of considering the quality of aggregates, the strength of concrete mixes made with various aggregates qualities (A, B, C, and D, as in Table 1) was drawn (Figure 9).
The results calculated with Bolomey’s model came from 84 studies [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109] of concrete mixes made with 100% coarse NA and 41 other studies [34,35,36,42,46,47,48,50,52,53,54,57,66,67,70,71,76,77,78,81,85,87,90,93,94,95,100,102,103,104,105,107,110,111,112,113,114,115] of concrete made with 100% coarse RA. The k values show that, for a 95% confidence interval, the scatter between the mixes made with NA (mostly classed as A in Table 1) was slightly smaller than that of the mixes made with RA (generally classed as B–D) (Figure 9a). This big scatter of the NA mixes allows one important conclusion—it is conceptually established that the quality of RA affects the strength of concrete, and the same is true for NA, but on a smaller scale, because the differences in quality are also smaller. In other words, the quality of the NA needs to be considered to understand the performance of concrete made with them (Figure 9a). Figure 9b was drawn based on the upper and lower boundaries of Figure 9b. This figure confirms the abovementioned facts demonstrated for concrete mixes made with NA only—as the quality of the aggregates (regardless of the source, i.e., NA or RA) decreases (A to D), the calculated/actual strength ratio increases, i.e., existing formulas overestimate the compressive strength the most for lower quality aggregates.

4. Conclusions

This study allows a better understanding of the compressive strength of concrete made with aggregates of various geological natures (e.g., limestone, basalt, granite, and quartz) and qualities (WA, density, and LA abrasion). The following conclusions can be drawn from this study.
The original (Abrams, Slater, and ACI) and modified (Bolomey and Feret) models cannot accurately estimate the compressive strength of concrete when the characteristics of aggregates are neglected. In other words, the estimated strength of concrete based on the quality of cement paste only is not accurate, and the relationship between the actual and calculated strength for all the original models is poor when only w/c (with and without considering the volume of aggregates to the cement content) is considered as an influencing factor.
The scatter between the calculated and experimental compressive strength of concrete, even if made with 100% NA, is significant. In other words, for the same mix composition (similar cement paste quality), there are significant differences between the results when various geological natures of NA (e.g., limestone, basalt, granite, sandstone) are used in concrete. The same is true when various qualities (WA, density, and LA abrasion) of aggregates are used.
The modified models (Bolomey and Feret) work better than the original models (Abrams, Slater, and ACI) because they consider the strength class of cement as one of the factors. However, Bolomey’s model does not consider the ratio of the volume of aggregates to cement paste, and Feret’s model does not consider how the aggregates are obtained (e.g., rolled or crushed) as influencing factors.
In most cases, the scatter between concrete mixes measured by the difference between the upper (k1) and lower (k2) boundaries (k = fcm, calculated/fcm, experimental) for a 95% confidence interval significantly decreased when they were split based on the geological nature of the aggregates used. The same occurred when the mixes were split based on the quality of their aggregates.
According to both modified models (Bolomey and Ferret), the calculated/actual strength ratio of the concrete mixes made with basalt is higher than that of the mixes with aggregates of other geological natures—in descending order, limestone, quartz, and granite. In terms of the physical characteristics of the aggregates, the calculated/actual strength ratio of concrete increases as the quality (high WA, low density, and LA abrasion) of the aggregates decreases.
In order to further show the importance of considering the physical characteristics of aggregates, the strength of a few examples of concrete made with aggregates of various qualities (A, B, C, and D, according to Table 1), namely incorporating 100% coarse RA or NA, was calculated using Bolomey’s model. For a 95% confidence interval, the scatter between the mixes made of NA (mostly classed as A) was slightly smaller than that of the mixes made with RA (generally classed as B–D), but still significant. This means that to estimate the compressive strength of concrete made with either NA or RA, the influence of the geological nature and physical quality cannot be ignored, and this should be included both in the standard formulas and in the codes.

Author Contributions

J.d.B. and R.K. conceived and designed the experiments; R.K. analyzed the data; P.R.d.S. contributed reagents/materials/analysis tools; J.d.B. and R.K. wrote the paper.

Acknowledgments

The authors appreciate the support of CERIS unit from IST-University of Lisbon and the Foundation for Science and Technology of Portugal.

Conflicts of Interest

The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.

References

  1. Feret, R. On the compactness of hydraulic mortars (in French–Sur la compacité des mortiers hydrauliques). Ann. Ponts Chaussées Sér. 1892, 7, 5–164. [Google Scholar]
  2. Abrams, L.D. Properties of Concrete, 3rd ed.; Pitman Publishing Ltd.: London, UK, 1919. [Google Scholar]
  3. Powers, T.; Brownyard, T. Studies of the Physical Properties of Hardened Portland Cement Paste; American Concrete Institute (ACI): Farmington Hills, MI, USA, 1946; Volume 18, pp. 669–712. [Google Scholar]
  4. Silva, R. Use of Recycled Aggregates from Construction and Demolition Wastes in the Production of Structural Concrete. Ph.D. Thesis, Universidade de Lisboa, Instituto Superior Técnico, Lisbon, Portugal, 2015. [Google Scholar]
  5. Mechling, J.; Lecomte, A.; Diliberto, C. Relation between cement composition and compressive strength of pure pastes. Cem. Concr. Compos. 2009, 31, 255–262. [Google Scholar] [CrossRef]
  6. Maruyama, I.; Igarashi, G. Cement reaction and resultant physical properties of cement paste. J. Adv. Concr. Technol. 2014, 12, 200–213. [Google Scholar] [CrossRef]
  7. Silva, R.V.; de Brito, J.; Dhir, R.K. Properties and composition of recycled aggregates from construction and demolition waste suitable for concrete production. Constr. Build. Mater. 2014, 65, 201–217. [Google Scholar] [CrossRef]
  8. Struble, L.; Skalny, J.; Mindess, S. A review of the cement-aggregate bond. Cem. Concr. Res. 1980, 10, 277–286. [Google Scholar] [CrossRef]
  9. Brandt, M. Optimization Methods for Material Design of Cement-Based Composites; CRC Press: Boca Raton, FL, USA, 2014; 328p. [Google Scholar]
  10. Bolomey, J. Granulation et prevision de la resistance probable des betons. Travoux 1935, 19, 228–232. [Google Scholar]
  11. Lijuan, K.; Yuanbo, D. Interfacial interaction of aggregate-cement paste in concrete. J. Wuhan Univ. Technol.-Mater. Sci. Ed. 2015, 30, 117–121. [Google Scholar] [CrossRef]
  12. Kurda, R.; de Brito, J.; Silvestre, J.D. Influence of recycled aggregates and high contents of fly ash on concrete fresh properties. Cem. Concr. Compos. 2017, 84, 198–213. [Google Scholar] [CrossRef]
  13. De Larrard, F. Concrete Mixture Proportioning: A Scientific Approach; CRC Press: London, UK, 1999; p. 448. [Google Scholar]
  14. Ollivier, J.P.; Maso, J.C.; Bourdette, B. Interfacial transition zone in concrete. Adv. Cem. Based Mater. 1995, 2, 30–38. [Google Scholar] [CrossRef]
  15. Behnood, A.; Behnood, V.; Gharehveran, M.M.; Alyamac, K.E. Prediction of the compressive strength of normal and high-performance concretes using M5P model tree algorithm. Constr. Build. Mater. 2017, 142, 199–207. [Google Scholar] [CrossRef]
  16. Chidiac, S.E.; Moutassem, F.; Mahmoodzadeh, F. Compressive strength model for concrete. Mag. Concr. Res. 2013, 65, 557–572. [Google Scholar] [CrossRef] [Green Version]
  17. Hicks, T. Civil Engineering Formulas, 2nd ed.; McGraw-Hill Education-Europe: New York, NY, USA, 2009; 416p. [Google Scholar]
  18. Slater, W.A. Relation of 7-day to 28-day compressive strength of mortar and concrete. J. Proc. 1926, 22, 437–449. [Google Scholar]
  19. ACI 2000-I. ACI Manual of Concrete Practice 2000, Part 1: Materials and General Properties of Concrete; American Concrete Institute (ACI): Farmington Hills, MI, USA, 2000. [Google Scholar]
  20. Karni, J. Prediction of compressive strength of concrete. Mater. Struct. 1974, 7, 197–200. [Google Scholar] [CrossRef]
  21. Popovics, S. New formulas for the prediction of the effect of porosity on concrete strength. ACI Mater. J. 1985, 82, 136–146. [Google Scholar]
  22. Popovics, S. History of a mathematical model for strength development of Portland cement concrete. ACI Mater. J. 1998, 95, 593–600. [Google Scholar]
  23. Popovics, S.; Ujhelyi, J. Contribution to the concrete strength versus water-cement ratio relationship. J. Mater. Civ. Eng. 2008, 20, 459–463. [Google Scholar] [CrossRef]
  24. Adewole, K.; Olutoge, F.; Habib, H. Effect of Nigerian Portland limestone cement grades on concrete compressive strength. Int. J. Civ. Environ. Struct. Constr. Archit. Eng. 2014, 8, 1199–1202. [Google Scholar]
  25. Faury, J. Le Béton; Dunod: Paris, France, 1958. (In French) [Google Scholar]
  26. Ajdukiewicz, A.B.; Kliszczewicz, A.T. Comparative tests of beams and columns made of recycled aggregate concrete and natural aggregate concrete. J. Adv. Concr. Technol. 2007, 5, 259–273. [Google Scholar] [CrossRef]
  27. Al-Swaidani, A.; Baddoura, M.; Aliyan, S.; Choeb, W. Assesment of alkali resistance of basalt used as concrete aggregates. SSP-J. Civ. Eng. 2015, 10, 17–27. [Google Scholar] [CrossRef]
  28. Bairagi, N.K.; Ravande, K.; Pareek, V.K. Behaviour of concrete with different proportions of natural and recycled aggregates. Resour. Conserv. Recyc. 1993, 9, 109–126. [Google Scholar] [CrossRef]
  29. Collins, F.; Sanjayan, J.G. Strength and shrinkage properties of alkali-activated slag concrete containing porous coarse aggregate. Cem. Concr. Res. 1999, 29, 607–610. [Google Scholar] [CrossRef]
  30. Dilbas, H.; Şimşek, M.; Çakır, Ö. An investigation on mechanical and physical properties of recycled aggregate concrete (RAC) with and without silica fume. Constr. Build. Mater. 2014, 61, 50–59. [Google Scholar] [CrossRef]
  31. Kishore, I.; Mounika, L.; Prasad, C.; Krishna, B. Experimental study on the use of basalt aggregate in concrete mixes. SSRG Int. J. Civ. Eng. 2015, 2, 39–42. [Google Scholar]
  32. Mittal, A.; Kaisare, M.; Shetti, R. Experimental study on use of fly ash in concrete. Use of SCC in a pump house at TAPP 3 & 4, Tarapur. Indian Concr. J. 2004, 78, 30–34. [Google Scholar]
  33. Özturan, T.; Çeçen, C. Effect of coarse aggregate type on mechanical properties of concretes with different strengths. Cem. Concr. Res. 1997, 27, 165–170. [Google Scholar] [CrossRef]
  34. Paine, K.; Collery, D.; Dhir, R. Strength and deformation characteristics of concrete containing coarse recycled and manufactured aggregates. In Proceedings of the 11th International Conference on Non-Conventional Materials and Technologies (NOCMAT 2009), Bath, UK, 6–9 September 2009; p. 9. [Google Scholar]
  35. Rahal, K. Mechanical properties of concrete with recycled coarse aggregate. Build. Environ. 2007, 42, 407–415. [Google Scholar] [CrossRef]
  36. Akbarnezhad, A.; Ong, K.C.G.; Zhang, M.H.; Tam, C.T.; Foo, T.W.J. Microwave-assisted beneficiation of recycled concrete aggregates. Constr. Build. Mater. 2011, 25, 3469–3479. [Google Scholar] [CrossRef]
  37. Barra, M.; Vázquez, E. Properties of concretes with recycled aggregates: Influence of properties of the aggregates and their interpretation. In Proceedings of the International Symposium on Sustainable Construction: Use of Recycled Concrete Aggregate, London, UK, 11–12 November 1998; pp. 19–30. [Google Scholar]
  38. Berndt, M.L. Properties of sustainable concrete containing fly ash, slag and recycled concrete aggregate. Constr. Build. Mater. 2009, 23, 2606–2613. [Google Scholar] [CrossRef]
  39. Bordelon, A.; Cervantes, V.; Roesler, J.R. Fracture properties of concrete containing recycled concrete aggregates. Mag. Concr. Res. 2009, 61, 665–670. [Google Scholar] [CrossRef]
  40. Bravo, M.; de Brito, J.; Pontes, J.; Evangelista, L. Performance of concrete made with recycled aggregates from Portuguese CDW recycling plants. Key Eng. Mater. 2015, 634, 193–205. [Google Scholar] [CrossRef]
  41. Butler, L.; West, J.S.; Tighe, S.L. The effect of recycled concrete aggregate properties on the bond strength between RCA concrete and steel reinforcement. Cem. Concr. Res. 2011, 41, 1037–1049. [Google Scholar] [CrossRef]
  42. Buyle-Bodin, F.; Hadjieva-Zaharieva, R. Influence of industrially produced recycled aggregates on flow properties of concrete. Mater. Struct. 2002, 35, 504–509. [Google Scholar] [CrossRef]
  43. Carro-López, D.; González-Fonteboa, B.; de Brito, J.; Martínez-Abella, F.; González-Taboada, I.; Silva, P. Study of the rheology of self-compacting concrete with fine recycled concrete aggregates. Constr. Build. Mater. 2015, 96, 491–501. [Google Scholar] [CrossRef]
  44. Cartuxo, F.; de Brito, J.; Evangelista, L.; Jiménez, J.R.; Ledesma, E.F. Rheological behaviour of concrete made with fine recycled concrete aggregates—Influence of the superplasticizer. Constr. Build. Mater. 2015, 89, 36–47. [Google Scholar] [CrossRef]
  45. Casuccio, M.; Torrijos, M.C.; Giaccio, G.; Zerbino, R. Failure mechanism of recycled aggregate concrete. Constr. Build. Mater. 2008, 22, 1500–1506. [Google Scholar] [CrossRef]
  46. Correia, J.; de Brito, J.; Pereira, A. Effects on concrete durability of using recycled ceramic aggregates. Mater. Struct. 2006, 39, 169–177. [Google Scholar] [CrossRef]
  47. Dapena, E.; Alaejos, P.; Lobet, A.; Pérez, D. Effect of recycled sand content on characteristics of mortars and concretes. J. Mater. Civ. Eng. 2011, 23, 414–422. [Google Scholar] [CrossRef]
  48. Debieb, F.; Kenai, S. The use of coarse and fine crushed bricks as aggregate in concrete. Constr. Build. Mater. 2008, 22, 886–893. [Google Scholar] [CrossRef]
  49. Abd Elhakam, A.; Mohamed, A.E.; Awad, E. Influence of self-healing, mixing method and adding silica fume on mechanical properties of recycled aggregates concrete. Constr. Build. Mater. 2012, 35, 421–427. [Google Scholar] [CrossRef]
  50. Etxeberria, M.; Vázquez, E.; Marí, A.; Barra, M. Influence of amount of recycled coarse aggregates and production process on properties of recycled aggregate concrete. Cem. Concr. Res. 2007, 37, 735–742. [Google Scholar] [CrossRef]
  51. Evangelista, L.; de Brito, J. Mechanical behaviour of concrete made with fine recycled concrete aggregates. Cem. Concr. Compos. 2007, 29, 397–401. [Google Scholar] [CrossRef]
  52. García-González, J.; Barroqueiro, T.; Evangelista, L.; de Brito, J.; de Belie, N.; Pozo, J.M.; Juan-Valdés, A. Fracture energy of coarse recycled aggregate concrete using the wedge splitting test method: Influence of water-reducing admixtures. Mater. Struct. 2017, 50, 120. [Google Scholar] [CrossRef]
  53. Gómez-Soberón, J.M.V. Porosity of recycled concrete with substitution of recycled concrete aggregate: An experimental study. Cem. Concr. Res. 2002, 32, 1301–1311. [Google Scholar] [CrossRef]
  54. Gonçalves, A.; Esteves, A.; Vieira, M. Influence of recycled concrete aggregates on concrete durability. In Proceedings of the International RILEM Conference on the Use of Recycled Materials in Buildings and Structures, Barcelona, Spain, 8–11 November 2004; pp. 554–562. [Google Scholar]
  55. Gonzalez-Corominas, A.; Etxeberria, M. Properties of high performance concrete made with recycled fine ceramic and coarse mixed aggregates. Constr. Build. Mater. 2014, 68, 618–626. [Google Scholar] [CrossRef]
  56. Knights, J. Relative performance of high quality concretes containing recycled aggregates and their use in construction. In Proceedings of the International Symposium on Sustainable Construction: Use of Recycled Concrete Aggregate, London, UK, 11–12 November 1998; pp. 275–286. [Google Scholar]
  57. Kou, S.C.; Poon, C.S.; Chan, D. Influence of fly ash as cement replacement on the properties of recycled aggregate concrete. J. Mater. Civ. Eng. 2007, 19, 709–717. [Google Scholar] [CrossRef]
  58. Kumar, P.; Dhinakaran, G. Effect of admixed recycled aggregate concrete on properties of fresh and hardened concrete. J. Mater. Civ. Eng. 2012, 24, 494–498. [Google Scholar] [CrossRef]
  59. Kurda, R. Sustainable Development of Cement-Based Materials: Application to Recycled Aggregates Concrete. Ph.D. Thesis, Universidade de Lisboa, Instituto Superior Técnico, Lisbon, Portugal, 2017. [Google Scholar]
  60. Kwan, W.H.; Ramli, M.; Kam, K.J.; Sulieman, M.Z. Influence of the amount of recycled coarse aggregate in concrete design and durability properties. Constr. Build. Mater. 2012, 26, 565–573. [Google Scholar] [CrossRef]
  61. Lotfy, A.; Al-Fayez, M. Performance evaluation of structural concrete using controlled quality coarse and fine recycled concrete aggregate. Cem. Concr. Compos. 2015, 61, 36–43. [Google Scholar] [CrossRef]
  62. Lima, C.; Caggiano, A.; Faella, C.; Martinelli, E.; Pepe, M.; Realfonzo, R. Physical properties and mechanical behaviour of concrete made with recycled aggregates and fly ash. Constr. Build. Mater. 2013, 47, 547–559. [Google Scholar] [CrossRef]
  63. Muhammad, M.; Abdullah, W.; Abdul-Kadir, M. Post-fire mechanical properties of concrete made with recycled tire rubber as fine aggregate replacement. Sulaimani J. Eng. Sci. 2017, 4, 74–85. [Google Scholar] [CrossRef]
  64. Pedro, D.; de Brito, J.; Evangelista, L. Influence of the crushing process of recycled aggregates on concrete properties. Key Eng. Mater. 2015, 634, 151–162. [Google Scholar] [CrossRef]
  65. Pepe, M. A Conceptual Model for Designing Recycled Aggregate Concrete for Structural Applications. Ph.D. Thesis, University of Salerno, Fisciano, Italy, 2015. [Google Scholar]
  66. Poon, C.; Kou, S. Effects of fly ash on mechanical properties of 10-year-old concrete prepared with recycled concrete aggregates. In Proceedings of the 2nd International Conference on Waste Engineering Management (ICWEM 2010), Shanghai, China, 13–15 October 2010; pp. 46–59. [Google Scholar]
  67. Poon, C.; Shui, Z.; Lam, L. Effect of microstructure of ITZ on compressive strength of concrete prepared with recycled aggregates. Constr. Build. Mater. 2004, 18, 461–468. [Google Scholar] [CrossRef]
  68. Poon, C.S.; Shui, Z.H.; Lam, L.; Fok, H.; Kou, S.C. Influence of moisture states of natural and recycled aggregates on the slump and compressive strength of concrete. Cem. Concr. Res. 2004, 34, 31–36. [Google Scholar] [CrossRef]
  69. Ravindrarajah, R.; Loo, Y.H.; Tam, C.T. Recycled concrete as fine and coarse aggregates in concrete. Mag. Concr. Res. 1987, 39, 214–220. [Google Scholar] [CrossRef]
  70. Razaqpur, A.G.; Fathifazl, G.; Isgor, B.; Abbas, A.; Fournier, B.; Foo, S. How to produce high quality concrete mixes with recycled concrete aggregate. In Proceedings of the 2nd International Conference on Waste Engineering Management (ICWEM 2010), Shanghai, China, 13–15 October 2010; pp. 11–35. [Google Scholar]
  71. Ridzuan, A.; Ibrahim, A.; Ismail, A.; Diah, A. Durability performance of recycled aggregate concrete. In Proceedings of the International Conference on Global construction: Ultimate Concrete Opportunities: Achieving Sustainability in Construction, London, UK, 5–6 July 2005; pp. 193–202. [Google Scholar]
  72. Safiuddin, M.; Alengaram, U.; Salam, M.; Jumaat, M.; Jaafar, F.; Saad, H. Properties of high-workability concrete with recycled concrete aggregate. Mater. Res. 2011, 14, 248–255. [Google Scholar] [CrossRef] [Green Version]
  73. Sarhat, S. An experimental investigation on the viability of using fine concrete recycled aggregate in concrete production. In Proceedings of the International Conference on Sustainable Construction Materials and Technologies, Coventry, UK, 1–13 June 2007; pp. 53–57. [Google Scholar]
  74. Soares, D.; de Brito, J.; Ferreira, J.; Pacheco, J. Use of coarse recycled aggregates from precast concrete rejects: Mechanical and durability performance. Constr. Build. Mater. 2014, 71, 263–272. [Google Scholar] [CrossRef]
  75. Surya, M.; Rao, V.; Parameswaran, L. Mechanical, durability, and time-dependent properties of recycled aggregate concrete with fly ash. ACI Mater. J. 2015, 112, 653–662. [Google Scholar] [CrossRef]
  76. Thomas, C.; Setién, J.; Polanco, J.A.; Alaejos, P.; de Juan, M.S. Durability of recycled aggregate concrete. Constr. Build. Mater. 2013, 40, 1054–1065. [Google Scholar] [CrossRef]
  77. Yang, K.; Chung, H.; Ashour, A. Influence of type and replacement level of recycled aggregates on concrete properties. ACI Mater. J. 2008, 105, 289–296. [Google Scholar]
  78. Yang, J.; Du, Q.; Bao, Y. Concrete with recycled concrete aggregate and crushed clay bricks. Constr. Build. Mater. 2011, 25, 1935–1945. [Google Scholar] [CrossRef]
  79. Wang, Z.; Wang, L.; Cui, Z.; Zhou, M. Effect of recycled coarse aggregate on concrete compressive strength. Trans. Tianjin Univ. 2011, 17, 229–234. [Google Scholar] [CrossRef]
  80. Kurad, R.; Silvestre, J.D.; de Brito, J.; Ahmed, H. Effect of incorporation of high volume of recycled concrete aggregates and fly ash on the strength and global warming potential of concrete. J. Clean. Prod. 2017, 166, 485–502. [Google Scholar] [CrossRef]
  81. Kenai, S.; Debieb, F.; Azzouz, L. Mechanical properties and durability of concrete made with coarse and fine recycled aggregates. In Proceedings of the International Symposium on Sustainable Concrete Construction, Dundee, Scotland, UK, 9–11 September 2002; pp. 383–392. [Google Scholar]
  82. Akça, K.R.; Çakır, Ö.; İpek, M. Properties of polypropylene fiber reinforced concrete using recycled aggregates. Constr. Build. Mater. 2015, 98, 620–630. [Google Scholar] [CrossRef]
  83. González, B.; Martínez, F. Shear strength of concrete with recycled aggregates. In Proceedings of the International RILEM Conference on the Use of Recycled Materials in Buildings and Structures, Barcelona, Spain, 8–11 November 2004; pp. 619–628. [Google Scholar]
  84. Medina, C.; de Rojas, M.I.S.; Frías, M. Properties of recycled ceramic aggregate concretes: Water resistance. Cem. Concr. Compos. 2013, 40, 21–29. [Google Scholar] [CrossRef] [Green Version]
  85. Park, S. Recycled Concrete Construction Rubble as Aggregate for New Concrete; Study Report No 86; BRANZ: Wellington, New Zealand, 1999; p. 20. [Google Scholar]
  86. Nagataki, S.; Gokce, A.; Saeki, T.; Hisada, M. Assessment of recycling process induced damage sensitivity of recycled concrete aggregates. Cem. Concr. Res. 2004, 34, 965–971. [Google Scholar] [CrossRef]
  87. Teranishi, K.; Dosho, Y.; Narikawa, M.; Kikuchi, M. Application of recycled aggregate concrete for structural concrete: Part 3-Production of recycled aggregate by real-scale plant and quality of recycled aggregate concrete. In Proceedings of the International Symposium on Sustainable Construction: Use of Recycled Concrete Aggregate, London, UK, 11–12 November 1998; pp. 143–156. [Google Scholar]
  88. Beltrán, M.G.; Barbudo, A.; Agrela, F.; Galvín, A.P.; Jiménez, J.R. Effect of cement addition on the properties of recycled concretes to reach control concretes strengths. J. Clean. Prod. 2014, 79, 124–133. [Google Scholar] [CrossRef]
  89. Chen, H.J.; Yen, T.; Chen, K.H. The use of building rubbles in concrete and mortar. J. Chin. Inst. Eng. 2003, 26, 227–236. [Google Scholar] [CrossRef]
  90. Choi, W.-C.; Yun, H.-D. Compressive behavior of reinforced concrete columns with recycled aggregate under uniaxial loading. Eng. Struct. 2012, 41, 285–293. [Google Scholar] [CrossRef]
  91. Corinaldesi, V.; Moriconi, G. Recycling of concrete in precast concrete production. In Proceedings of the Sustainable Construction Materials and Technologies, London, UK, 11–13 June 2007; pp. 69–75. [Google Scholar]
  92. Corinaldesi, V.; Moriconi, G. Concrete and mortar performance by using recycled aggregates. In Proceedings of the International Conference on Sustainable Waste Management and Recycling: Construction Demolition Waste, London, UK, 14–15 September 2004; pp. 157–164. [Google Scholar]
  93. Dhir, R.K.; Paine, K.A. Performance Related Approach to the Use of Recycled Aggregates; Waste and Resources Action Programme (WRAP) Aggregates Research Programme: Banbury, Oxon, UK, 2007; p. 77. [Google Scholar]
  94. Dhir, R.K.; MLimbachiya, C.; Leelawat, T. Suitability of recycled concrete aggregate for use in bs 5328 designated mixes. Proc. Inst. Civ. Eng.-Struct. Build. 1999, 134, 257–274. [Google Scholar] [CrossRef]
  95. Dhir, R.K.; Paine, K.A.; O’Leary, S. Use of recycled concrete aggregate in concrete pavement construction: A case study. In Proceedings of the International Symposium on Sustainable Waste Management, Dundee, Scotland, UK, 9–11 September 2003; pp. 373–382. [Google Scholar]
  96. Dolara, E.; Di Niro, G.; Cairns, R. Recycled aggregate concrete prestressed beams. In Proceedings of the International Symposium on Sustainable Construction: Use of Recycled Concrete Aggregate, London, UK, 11–12 November 1998; pp. 255–261. [Google Scholar]
  97. Domingo-Cabo, A.; Lázaro, C.; López-Gayarre, F.; Serrano-López, M.A.; Serna, P.; Castaño-Tabares, J.O. Creep and shrinkage of recycled aggregate concrete. Constr. Build. Mater. 2009, 23, 2545–2553. [Google Scholar] [CrossRef]
  98. Dosho, Y. Development of a sustainable concrete waste recycling system—Application of recycled aggregate concrete produced by aggregate replacing method. J. Adv. Concr. Technol. 2007, 5, 27–42. [Google Scholar] [CrossRef]
  99. Fan, C.-C.; Huang, R.; Hwang, H.; Chao, S.-J. Properties of concrete incorporating fine recycled aggregates from crushed concrete wastes. Constr. Build. Mater. 2016, 112, 708–715. [Google Scholar] [CrossRef]
  100. Juan, M.S.; Gutiérrez, P.A. Influence of recycled aggregate quality on concrete properties. In Proceedings of the International RILEM Conference on the Use of Recycled Materials in Buildings and Structures, Barcelona, Spain, 8–11 November 2004; pp. 545–553. [Google Scholar]
  101. Khatib, J.M. Properties of concrete incorporating fine recycled aggregate. Cem. Concr. Res. 2005, 35, 763–769. [Google Scholar] [CrossRef]
  102. Kim, S.-W.; Yun, H.-D. Influence of recycled coarse aggregates on the bond behavior of deformed bars in concrete. Eng. Struct. 2013, 48, 133–143. [Google Scholar] [CrossRef]
  103. Kim, K.; Shin, M.; Cha, S. Combined effects of recycled aggregate and fly ash towards concrete sustainability. Constr. Build. Mater. 2013, 48, 499–507. [Google Scholar] [CrossRef]
  104. Koulouris, A.; Limbachiya, M.C.; Fried, A.N.; Roberts, J.J. Use of recycled aggregate in concrete application: Case studies. In Proceedings of the International Conference on Sustainable Waste Management and Recycling: Challenges and Opportunities, London, UK, 14–15 September 2004; pp. 245–257. [Google Scholar]
  105. Limbachiya, M.; Meddah, M.S.; Ouchagour, Y. Use of recycled concrete aggregate in fly-ash concrete. Constr. Build. Mater. 2012, 27, 439–449. [Google Scholar] [CrossRef]
  106. Otsuki, N.; Miyazato, S.-I.; Yodsudjai, W. Influence of recycled aggregate on interfacial transition zone, strength, chloride penetration and carbonation of concrete. J. Mater. Civ. Eng. 2003, 15, 443–451. [Google Scholar] [CrossRef]
  107. Rao, M.; Bhattacharyya, S.; Barai, S. Influence of recycled aggregate on mechanical properties of concrete. In Proceedings of the 5th Civil Engineering Conference in the Asian Region and Australasian Structural Engineering Conference, Sydney, Australia, 8–12 August 2010; pp. 749–754. [Google Scholar]
  108. Waleed, N.; Canisius, T. Engineering Properties of Concrete Containing Recycled Aggregates; Waste and Resources Action Programme: Banbury, UK, 2007; p. 104. [Google Scholar]
  109. Zhou, C.; Chen, Z. Mechanical properties of recycled concrete made with different types of coarse aggregate. Constr. Build. Mater. 2017, 134, 497–506. [Google Scholar] [CrossRef]
  110. Corinaldesi, V.; Moriconi, G. Influence of mineral additions on the performance of 100% recycled aggregate concrete. Constr. Build. Mater. 2009, 23, 2869–2876. [Google Scholar] [CrossRef]
  111. Padmini, A.K.; Ramamurthy, K.; Mathews, M.S. Influence of parent concrete on the properties of recycled aggregate concrete. Constr. Build. Mater. 2009, 23, 829–836. [Google Scholar] [CrossRef]
  112. Yanagi, K.; Kasai, Y.; Kaga, S.; Abe, M. Experimental study on the applicability of recycled aggregate concrete to cast-in-place concrete pile. In Sustainable Construction: Use of Recycled Concrete Aggregate; Thomas Telford: London, UK, 2015; pp. 359–370. [Google Scholar]
  113. Kou, S.; Poon, C. Properties of self-compacting concrete prepared with coarse and fine recycled concrete aggregates. Cem. Concr. Compos. 2009, 31, 622–627. [Google Scholar] [CrossRef]
  114. Lin, Y.-H.; Tyan, Y.-Y.; Chang, T.-P.; Chang, C.-Y. An assessment of optimal mixture for concrete made with recycled concrete aggregates. Cem. Concr. Res. 2004, 34, 1373–1380. [Google Scholar] [CrossRef]
  115. Pedro, D.; de Brito, J.; Evangelista, L. Mechanical characterization of high performance concrete prepared with recycled aggregates and silica fume from the precast industry. J. Clean. Prod. 2017, 164, 939–949. [Google Scholar] [CrossRef]
  116. Kurda, R.; Silvestre, J.D.; de Brito, J.; Ahmed, H. Optimizing recycled concrete containing high volume of fly ash in terms of the embodied energy and chloride ion resistance. J. Clean. Prod. 2018. [Google Scholar] [CrossRef]
  117. Kurda, R.; de Brito, J.; Silvestre, J.D. Indirect evaluation of the compressive strength of recycled aggregate concrete with high fly ash ratios. Mag. Concr. Res. 2018, 70, 204–216. [Google Scholar] [CrossRef]
  118. FIB Bullten 42. Constitutive Modelling of High Strength/High Performance Concrete; International Federation for Structural Concrete (FIB): Lausanne, Switzerland, 2008. [Google Scholar]
  119. Gul, M. Effect of cube size on the compressive strength of concrete. Int. J. Eng. Dev. Res. 2016, 4, 956–959. [Google Scholar]
  120. Neville, A.M. Properties of Concrete, 4th ed.; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
  121. Felekoğlu, B.; Türkel, S. Effects of specimen type and dimensions on compressive strength of concrete. GU J. Sci. 2005, 18, 639–645. [Google Scholar]
  122. Gonnerman, H. Effect of size and shape of test specimen on compressive strength of concrete. Proc. ASTM 1925, 25, 237–250. [Google Scholar]
  123. Nasser, K.; Al-Manaseer, A. It’s time for a change from 6_12 to 3_6 inch cylinders. ACI Mater. J. 1987, 84, 6–213. [Google Scholar]
  124. Malhotra, V. Are 4 × 8 Inch concrete cylinders as good as 6 × 12 Inch cylinder for quality control concrete? ACI J. 1976, 73, 33–36. [Google Scholar]
  125. Forstie, D.; Schnormeier, R. Development and Use of 4 × 8 in. Concrete Cylinders in Arizona. Concr. Int. 1981, 3, 41–45. [Google Scholar]
  126. Carrasquillo, R.; Nilson, A.; State, F. Propeties of high strength concrete subject to short-term loads. ACI J. 1981, 78, 42–45. [Google Scholar]
  127. Lessard, M.; Aitcin, P. Testing of High Performance Concrete, High Performance Concrete; E & FN Spon: London, UK, 1992; pp. 196–213. [Google Scholar]
  128. Halstead, P.E. The early history of Portland cement. Trans. Newcom. Soc. 1961, 34, 37–54. [Google Scholar] [CrossRef]
  129. Lea, F.; Mason, T. Cement; Encyclopædia Britannica, Inc.: Chicago, IL, USA, 2015. [Google Scholar]
  130. Bruhl, R. Understanding Statistical Analysis and Modeling; SAGE Publications: Thousand Oaks, CA, USA, 2017; p. 440. ISBN 9781506317373. [Google Scholar]
  131. Dahlquist, G.; Bjorck, A. Numerical Methods in Scientific Computing: Volume 1; SIAM: Philadelphia, PA, USA, 2008; p. 717. ISBN 9780898717785. [Google Scholar]
  132. Ingham, J.P. 4-Aggregates. In Geomaterials under the Microscope; Academic Press: Boston, MA, USA, 2013; pp. 61–74. [Google Scholar]
  133. Gill, R. Igneous Rocks and Processes: A Practical Guide; Wiley-Blackwell: Hoboken, NJ, USA, 2010; p. 438. [Google Scholar]
Applsci 08 01095 g001 550
Figure 1. Relationship between the compressive strength “fcm, cylinder 150 mm x 300 mm length” and w/c ratio of concrete.
Figure 1. Relationship between the compressive strength “fcm, cylinder 150 mm x 300 mm length” and w/c ratio of concrete.
Applsci 08 01095 g001
Applsci 08 01095 g002 550
Figure 2. Relationship between the actual and calculated compressive strength of concrete mixes made with NA sourced from different geological natures. The strength values were calculated according to the (a) Abrams, (b) Slater and (c) ACI formulas. k = (fcm, calculated/fcm, experimental).
Figure 2. Relationship between the actual and calculated compressive strength of concrete mixes made with NA sourced from different geological natures. The strength values were calculated according to the (a) Abrams, (b) Slater and (c) ACI formulas. k = (fcm, calculated/fcm, experimental).
Applsci 08 01095 g002
Applsci 08 01095 g003 550
Figure 3. Relationship between the actual and calculated compressive strength of concrete mixes made with NA sourced from different geological natures. The strength values were calculated according to the (a) Bolomey and (b) Feret formulas. k = (fcm, calculated/fcm, experimental).
Figure 3. Relationship between the actual and calculated compressive strength of concrete mixes made with NA sourced from different geological natures. The strength values were calculated according to the (a) Bolomey and (b) Feret formulas. k = (fcm, calculated/fcm, experimental).
Applsci 08 01095 g003
Applsci 08 01095 g004 550
Figure 4. Relationship between the actual and calculated compressive strength of concrete mixes made with NA sourced from different geological natures. k1 and k2 are the upper and lower boundaries for a 95% confidence interval, respectively, according to the (a) Bolomey and (b) Feret models.
Figure 4. Relationship between the actual and calculated compressive strength of concrete mixes made with NA sourced from different geological natures. k1 and k2 are the upper and lower boundaries for a 95% confidence interval, respectively, according to the (a) Bolomey and (b) Feret models.
Applsci 08 01095 g004
Applsci 08 01095 g005 550
Figure 5. Relationship between the actual and calculated compressive strength of concrete mixes made with NA sourced from different geological natures. The average k value is the average of k1 and k2 from Figure 4, according to the (a) Bolomey and (b) Feret models. The standard deviation for the k values was ≈0.20 in both models.
Figure 5. Relationship between the actual and calculated compressive strength of concrete mixes made with NA sourced from different geological natures. The average k value is the average of k1 and k2 from Figure 4, according to the (a) Bolomey and (b) Feret models. The standard deviation for the k values was ≈0.20 in both models.
Applsci 08 01095 g005
Applsci 08 01095 g006 550
Figure 6. Factors that affect the influence of aggregates on concrete quality.
Figure 6. Factors that affect the influence of aggregates on concrete quality.
Applsci 08 01095 g006
Applsci 08 01095 g007 550
Figure 7. Relationship between the actual and calculated compressive strength of the concrete mixes made with NA, classified in terms of their quality. The physical quality of A-I aggregates is better than that of A-II aggregates, followed by B-I aggregates. k1 and k2 are the upper and lower boundaries for the 95% confidence intervals, respectively, according to the (a) Bolomey and (b) Feret models.
Figure 7. Relationship between the actual and calculated compressive strength of the concrete mixes made with NA, classified in terms of their quality. The physical quality of A-I aggregates is better than that of A-II aggregates, followed by B-I aggregates. k1 and k2 are the upper and lower boundaries for the 95% confidence intervals, respectively, according to the (a) Bolomey and (b) Feret models.
Applsci 08 01095 g007
Applsci 08 01095 g008 550
Figure 8. Relationship between the actual and calculated compressive strength of concrete mixes made with NA, classified in terms of their quality. The physical quality of the A-I aggregates is better than that of A-II, then followed by B-I. The average k value is the average of k1 and k2 from Figure 7, according to the (a) Bolomey and (b) Feret models. The standard deviation for the k values was ≈0.25 in both models.
Figure 8. Relationship between the actual and calculated compressive strength of concrete mixes made with NA, classified in terms of their quality. The physical quality of the A-I aggregates is better than that of A-II, then followed by B-I. The average k value is the average of k1 and k2 from Figure 7, according to the (a) Bolomey and (b) Feret models. The standard deviation for the k values was ≈0.25 in both models.
Applsci 08 01095 g008
Applsci 08 01095 g009 550
Figure 9. Relationship between the actual and calculated compressive strength of concrete mixes made with 100% NA and RA classified in terms of their quality. The strength was calculated according to Bolomey’s model. The physical quality of A aggregates is better than B, followed by C and D. (a) k values for NA and RA concrete mixes, (b) k1 and k2 are the upper and lower boundaries for the 95% confidence intervals, and (c) the average k value is the average of k1 and k2 from Figure 9b. The standard deviation for the k values was ≈0.51 in (c).
Figure 9. Relationship between the actual and calculated compressive strength of concrete mixes made with 100% NA and RA classified in terms of their quality. The strength was calculated according to Bolomey’s model. The physical quality of A aggregates is better than B, followed by C and D. (a) k values for NA and RA concrete mixes, (b) k1 and k2 are the upper and lower boundaries for the 95% confidence intervals, and (c) the average k value is the average of k1 and k2 from Figure 9b. The standard deviation for the k values was ≈0.51 in (c).
Applsci 08 01095 g009
Table
Table 1. Physical boundaries for each proposed class of aggregates [7].
Table 1. Physical boundaries for each proposed class of aggregates [7].
Aggregate ClassABCD
IIIIIIIIIIIIIIIIII
Minimum oven-dried density (kg/m3)260025002400230022002100200019001800No limit
Maximum water absorption (%)1.52.53.556.58.510.51315
Maximum LA abrasion mass loss (%)40 45 50
Table
Table 2. Formulas to calculate the compressive strength of concrete.
Table 2. Formulas to calculate the compressive strength of concrete.
ModelFormula a,bNotes/Limitations
Abram f cm = A B w / c The constants A and B are 96 MPa and 7, respectively. The w/c ratio should be between 0.3 and 1.2
Slater f cm = 0.007   · ( 2700   · C w − 760 ) This formula can be used only for mixes without SP
American Concrete Institute Manual of Concrete Practice (ACI2000-I) f cm = 117.07   · e − 2.572 · w / c The w/c ratio and cement content of the concrete mixes are limited to 0.41–0.82 and 300–360 kg/m3, respectively. The equation was adapted from the results of the table given in the specification with R2 = 0.996
Bolomey f cm = A 1   · ( 1 w / c − 0.5 ) if w/c > 0.4
f cm = A 2   · ( 1 w / c + 0.5 ) if w/c ≤ 0.4		The constants (A1 and A2) depend on the way aggregates are produced and on the strength class of cement (Table 3)
Feret f cm = k   · ( v v + I ) 2 The constant, k, depends on the strength class of cement. It is 265–290 and 315–350 for cement class CEM I 32.5 and 42.5, respectively; v is the absolute volume of cement paste and I is the volume index (air and water contents)
ac and w are the cement and water contents, respectively. In other words, w/c is the water to cement ratio; b fcm is the average compressive strength of the concrete in cylinders (150 mm diameter × 300 mm length) at 28 days (MPa).
Table
Table 3. Constants in Bolomey’s formula.
Table 3. Constants in Bolomey’s formula.
Aggregatew/cConstants aStrength Class of Cement (MPa)
2535404552.555
Natural (rolled)>0.40A113.7317.6519.6120.5922.067522.56
Natural (rolled)≤0.40A29.3211.712.7514.2214.587514.71
Natural (crushed)>0.40A115.219.6121.5723.5425.0125.5
Natural (crushed)≤0.40A210.313.2414.2215.6916.792517.16
a The constant between the presented strength class was determined by interpolation and the average value of the rolled and crushed aggregates was considered if information on the way the aggregates were produced was not provided.
Table
Table 4. Statistical data from the selected studies.
Table 4. Statistical data from the selected studies.
References aAggregatesCementMix CompositionStrength
Geological
Nature		Physical
Properties		Oven-Dried Particle Density (kg/m3)WA-24h (%)PropertiesMax. Aggregate Size (mm)Los Angeles (LA) Abrasion (%)Cement Type/StrengthCement Content (kg/m3)w/cWater Content (L/m3)fcm, cyl 150 × 300 (MPa)
[26,27,28,29,30,31,32,33,34,35]BasaltAI2716–29150.68–1.60Crushed14–2017–24CEM I 42.5–52.5300–5000.24–0.70108–21020–62
[26,27,31,33,34,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80]LimestoneAI-BI2277–27390.20–5.00Crushed/
rounded		10–3210–42CEM I 32.5–52.5210–6770.28–0.86126–26610–69
[26,81,82,83,84]QuartzAI2624–27800.17–1.5Crushed/
rounded		16–3224–36CEM I 42.5300–5000.36–0.61148–21422–59
[85,86,87]SandstoneAI2625–26600.50–0.94Crushed19–20-CEM I 42.5250–4630.40–0.60153–18523–56
[34,50,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109]Natural gravel (N.G.) bAI-AII2511–27190.05–2.5Crushed/
rounded		15–2520–30CEM I 42.5214–6350.32–0.84148–25915–52
a The following studies [34,35,36,42,46,47,48,50,52,53,54,57,66,67,70,71,76,77,78,81,85,87,90,93,94,95,100,102,103,104,105,107,110,111,112,113,114,115,116,117] were considered to study the effects of quality of aggregates on the compressive strength of concrete made with 100% coarse recycled aggregates (RA); b N.G.—the geological nature of the natural aggregates (NA) is not given.
Table
Table 5. The “fcm, cylinder 150 × 300 to fcm, cylinder 100 × 200” ratio in different studies.
Table 5. The “fcm, cylinder 150 × 300 to fcm, cylinder 100 × 200” ratio in different studies.
Studiesfcm, cylinder 150 × 300 to fcm, cylinder 100 × 200 RatioStrength [MPa]
Malhotra [124]0.84~46
Forstie and Schnormeier [125]0.87~48
Carrasquillo et al. [126]0.9348–80
Lessaed and Aitcin [127]0.9535–122
Average over 33 MPa0.90

Share and Cite

MDPI and ACS Style

De Brito, J.; Kurda, R.; Raposeiro da Silva, P. Can We Truly Predict the Compressive Strength of Concrete without Knowing the Properties of Aggregates? Appl. Sci. 2018, 8, 1095. https://doi.org/10.3390/app8071095

AMA Style

De Brito J, Kurda R, Raposeiro da Silva P. Can We Truly Predict the Compressive Strength of Concrete without Knowing the Properties of Aggregates? Applied Sciences. 2018; 8(7):1095. https://doi.org/10.3390/app8071095

Chicago/Turabian Style

De Brito, Jorge, Rawaz Kurda, and Pedro Raposeiro da Silva. 2018. "Can We Truly Predict the Compressive Strength of Concrete without Knowing the Properties of Aggregates?" Applied Sciences 8, no. 7: 1095. https://doi.org/10.3390/app8071095

APA Style

De Brito, J., Kurda, R., & Raposeiro da Silva, P. (2018). Can We Truly Predict the Compressive Strength of Concrete without Knowing the Properties of Aggregates? Applied Sciences, 8(7), 1095. https://doi.org/10.3390/app8071095

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop