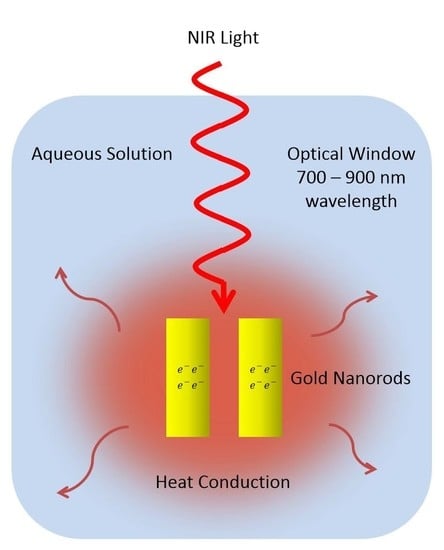
The Effect of Gold Nanorods Clustering on Near-Infrared Radiation Absorption
Abstract
:Featured Application
Abstract
1. Introduction
2. Methods
2.1. Optical Experiment
2.2. Thermal Experiment
2.3. Numerical Methods
3. Results and Discussion
3.1. Experimental Results
3.2. Numerical Predictions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alves, A.F.; Mendo, S.G.; Ferreira, L.P.; Mendonça, M.H.; Ferreira, P.; Godinho, M.; Cruz, M.M.; Carvalho, M.D. Gelatine-assisted synthesis of magnetite nanoparticles for magnetic hyperthermia. J. Nanopart. Res. 2016, 18, 1–13. [Google Scholar] [CrossRef]
- Austin, L.A.; Mackey, M.A.; Dreaden, E.C.; El-Sayed, M.A. The optical, photothermal, and facile surface chemical properties of gold and silver nanoparticles in biodiagnostics, therapy, and drug delivery. Arch. Toxicol. 2014, 88, 1391–1417. [Google Scholar] [CrossRef] [PubMed]
- Bayazitoglu, Y.; Kheradmand, S.; Tullius, T.K. An overview of nanoparticle assisted laser therapy. Int. J. Heat Mass Transf. 2013, 67, 469–486. [Google Scholar] [CrossRef]
- Huang, X.; El-Sayed, M.A. Plasmonic photo-thermal therapy (pptt). Alex. J. Med. 2011, 47, 1–9. [Google Scholar] [CrossRef]
- Huang, X.; Jain, P.K.; El-Sayed, I.H.; El-Sayed, M.A. Plasmonic photothermal therapy (pptt) using gold nanoparticles. Lasers Med. Sci. 2008, 23, 217–228. [Google Scholar] [CrossRef] [PubMed]
- Melancon, M.P.; Lu, W.; Yang, Z.; Zhang, R.; Cheng, Z.; Elliot, A.M.; Stafford, J.; Olson, T.; Zhang, J.Z.; Li, C. In vitro and in vivo targeting of hollow gold nanoshells directed at epidermal growth factor receptor for photothermal ablation therapy. Mol. Cancer Ther. 2008, 7, 1730–1739. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Neal, D.P.; Hirsch, L.R.; Halas, N.J.; Payne, J.D.; West, J.L. Photo-thermal tumor ablation in mice using near infrared-absorbing nanoparticles. Cancer Lett. 2004, 209, 171–176. [Google Scholar] [CrossRef] [PubMed]
- Thovhogi, N.; Sibuyi, N.; Meyer, M.; Onani, M.; Madiehe, A. Targeted delivery using peptide-functionalised gold nanoparticles to white adipose tissues of obese rats. J. Nanopart. Res. 2015, 17, 112–120. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.; Wang, Y.; Liu, Z.; Fu, L.; Hu, L. Enhancement of radiation effect and increase of apoptosis in lung cancer cells by thio-glucose-bound gold nanoparticles at megavoltage radiation energies. J. Nanopart. Res. 2013, 15, 1642–1654. [Google Scholar] [CrossRef]
- Huang, X.; El-Sayed, I.H.; Qian, W.; El-Sayed, M.A. Cancer cell imaging and photothermal therapy in the near-infrared region by using gold nanorods. J. Am. Chem. Soc. 2006, 128, 2115–2120. [Google Scholar] [CrossRef] [PubMed]
- Knight, D.A.; Nita, R.; Moore, M.; Zabetakis, D.; Khandelwal, M.; Martin, B.D.; Fontana, J.; Goldberg, E.; Funk, A.R.; Chang, E.L. Surface plasmon resonance promotion of homogeneous catalysis using a gold nanoparticle platform. J. Nanopart. Res. 2014, 16, 2400–2412. [Google Scholar] [CrossRef]
- Mackey, M.A.; Ali, M.R.; Austin, L.A.; Near, R.D.; El-Sayed, M.A. The most effective gold nanorod size for plasmonic photothermal therapy: Theory and in vitro experiments. J. Phys. Chem. B 2014, 118, 1319–1326. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Dong, B.; Chen, B.; Jiang, Z.; Song, H. Selective photothermal therapy for breast cancer with targeting peptide modified gold nanorods. Dalton Trans. 2012, 41, 11134–11144. [Google Scholar] [CrossRef] [PubMed]
- Dombrovsky, L.A.; Timchenko, V.; Jackson, M. Indirect heating strategy for laser induced hyperthermia: An advanced thermal model. Int. J. Heat Mass Transf. 2012, 55, 4688–4700. [Google Scholar] [CrossRef]
- Dombrovsky, L.A.; Timchenko, V.; Pathak, C.; Piazena, H.; Müller, W.; Jackson, M. Radiative heating of superficial human tissues with the use of water-filtered infrared—A radiation: A computational modeling. Int. J. Heat Mass Transf. 2015, 85, 311–320. [Google Scholar] [CrossRef]
- Bashkatov, A.; Genina, E.; Kochubey, V.; Tuchin, V. Optical properties of human skin, subcutaneous and mucous tissues in the wavelength range from 400 to 2000 nm. J. Phys. D Appl. Phys. 2005, 38, 2543–2555. [Google Scholar] [CrossRef]
- Jacques, S.L. Corrigendum: Optical properties of biological tissues: A review. Phys. Med. Biol. 2013, 58, 5007–5008. [Google Scholar] [CrossRef]
- Maksimova, I.L.; Akchurin, G.G.; Khlebtsov, B.N.; Terentyuk, G.S.; Akchurin, G.G.; Ermolaev, I.A.; Skaptsov, A.A.; Soboleva, E.P.; Khlebtsov, N.G.; Tuchin, V.V. Near-infrared laser photothermal therapy of cancer by using gold nanoparticles: Computer simulations and experiment. Med. Laser Appl. 2007, 22, 199–206. [Google Scholar] [CrossRef]
- Lee, S.E.; Sasaki, D.Y.; Perroud, T.D.; Yoo, D.; Patel, K.D.; Lee, L.P. Biologically functional cationic phospholipid−gold nanoplasmonic carriers of RNA. J. Am. Chem. Soc. 2009, 131, 14066–14074. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; El-Sayed, M.A. Gold nanoparticles: Optical properties and implementations in cancer diagnosis and photothermal therapy. J. Adv. Res. 2010, 1, 13–28. [Google Scholar] [CrossRef]
- Huang, X.; Jain, P.K.; El-Sayed, I.H.; El-Sayed, M.A. Gold nanoparticles: Interesting optical properties and recent applications in cancer diagnostics and therapy. Nanomedicine 2007, 2, 681–693. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Neretina, S.; El-Sayed, M.A. Gold nanorods: From synthesis and properties to biological and biomedical applications. Adv. Mater. 2009, 21, 4880–4910. [Google Scholar] [CrossRef] [PubMed]
- Loo, C.; Lowery, A.; Halas, N.; West, J.; Drezek, R. Immunotargeted nanoshells for integrated cancer imaging and therapy. Nano Lett. 2005, 5, 709–711. [Google Scholar] [CrossRef] [PubMed]
- Jain, P.K.; Eustis, S.; El-Sayed, M.A. Plasmon coupling in nanorod assemblies: Optical absorption, discrete dipole approximation simulation, and exciton-coupling model. J. Phys. Chem. B 2006, 110, 18243–18253. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Gao, T.; Hong, H.; Sun, J. Applications of gold nanoparticles in cancer nanotechnology. Nanotechnol. Sci. Appl. 2008, 2008, 17–32. [Google Scholar] [CrossRef]
- Caswell, K.; Wilson, J.N.; Bunz, U.H.; Murphy, C.J. Preferential end-to-end assembly of gold nanorods by biotin-streptavidin connectors. J. Am. Chem. Soc. 2003, 125, 13914–13915. [Google Scholar] [CrossRef] [PubMed]
- Nikoobakht, B.; Wang, Z.; El-Sayed, M. Self-assembly of gold nanorods. J. Phys. Chem. B 2000, 104, 8635–8640. [Google Scholar] [CrossRef]
- Sun, Z.; Ni, W.; Yang, Z.; Kou, X.; Li, L.; Wang, J. Ph-controlled reversible assembly and disassembly of gold nanorods. Small 2008, 4, 1287–1292. [Google Scholar] [CrossRef] [PubMed]
- Jain, P.K.; El-Sayed, M.A. Surface plasmon coupling and its universal size scaling in metal nanostructures of complex geometry: Elongated particle pairs and nanosphere trimers. J. Phys. Chem. C 2008, 112, 4954–4960. [Google Scholar] [CrossRef]
- Kaneti, Y.V.; Chen, C.; Liu, M.; Wang, X.; Yang, J.L.; Taylor, R.A.; Jiang, X.; Yu, A. Carbon-coated gold nanorods: A facile route to biocompatible materials for photothermal applications. ACS Appl. Mater. Interfaces 2015, 7, 25658–25668. [Google Scholar] [CrossRef] [PubMed]
- Soni, S.; Tyagi, H.; Taylor, R.A.; Kumar, A. Role of optical coefficients and healthy tissue-sparing characteristics in gold nanorod-assisted thermal therapy. Int. J. Hyperth. 2013, 29, 87–97. [Google Scholar] [CrossRef] [PubMed]
- Soni, S.; Tyagi, H.; Taylor, R.A.; Kumar, A. Investigation on nanoparticle distribution for thermal ablation of a tumour subjected to nanoparticle assisted thermal therapy. J. Therm. Biol. 2014, 43, 70–80. [Google Scholar] [CrossRef] [PubMed]
- Soni, S.; Tyagi, H.; Taylor, R.A.; Kumar, A. The influence of tumour blood perfusion variability on thermal damage during nanoparticle-assisted thermal therapy. Int. J. Hyperth. 2015, 31, 615–625. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R.A.; Wong, J.K.; Baek, S.; Hewakuruppu, Y.; Jiang, X.; Chen, C.; Gunawan, A. Nanoparticle-assisted heating utilizing a low-cost white light source. J. Nanotechnol. Eng. Med. 2013, 4, 040903. [Google Scholar] [CrossRef]
- Gu, X.; Timchenko, V.; Yeoh, G.H.; Dombrovsky, L.A.; Taylor, R.A. Heat Generation in Gold Nanorods Solutions Due to Absorption of Near-Infrared Radiation; ICHMT Digital Library Online; Begel House: Napoli, Italy, 2017. [Google Scholar]
- Lee, S.E.; Liu, G.L.; Kim, F.; Lee, L.P. Remote optical switch for localized and selective control of gene interference. Nano Lett. 2009, 9, 562–570. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wang, Z.; Chen, X.; Xu, H.; Liu, J. Chitosan-capped gold nanoparticles for selective and colorimetric sensing of heparin. J. Nanopart. Res. 2013, 15, 1930–1939. [Google Scholar] [CrossRef] [PubMed]
- Pamies, R.; Cifre, J.G.H.; Espín, V.F.; Collado-González, M.; Baños, F.G.D.; de la Torre, J.G. Aggregation behavior of gold nanoparticles in saline aqueous media. J. Nanopart. Res. 2014, 16, 2376. [Google Scholar] [CrossRef]
- Umar, A.; Choi, S.-M. Aggregation behavior of oppositely charged gold nanorods in aqueous solution. J. Phys. Chem. C 2013, 117, 11738–11743. [Google Scholar] [CrossRef]
- Sambles, J. Polarized Light in Optics and Spectroscopy. J. Mod. Opt. 1991, 38, 1204–1205. [Google Scholar] [CrossRef]
- Zhang, M.; Kim, H.S.; Jin, T.; Moon, W.K. Near-infrared photothermal therapy using egfr-targeted gold nanoparticles increases autophagic cell death in breast cancer. J. Photochem. Photobiol. B Biol. 2017, 170, 58–64. [Google Scholar] [CrossRef] [PubMed]
- DeVoe, H. Optical properties of molecular aggregates. I. Classical model of electronic absorption and refraction. J. Chem. Phys. 1964, 41, 393–400. [Google Scholar] [CrossRef]
- Draine, B.T.; Flatau, P.J. User guide for the discrete dipole approximation code ddscat 7.3. arXiv, 2013; arXiv:1305.6497. [Google Scholar]
- Draine, B.T.; Flatau, P.J. Discrete-dipole approximation for scattering calculations. JOSA A 1994, 11, 1491–1499. [Google Scholar] [CrossRef]
- Lee, K.-S.; El-Sayed, M.A. Dependence of the enhanced optical scattering efficiency relative to that of absorption for gold metal nanorods on aspect ratio, size, end-cap shape, and medium refractive index. J. Phys. Chem. B 2005, 109, 20331–20338. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Juste, J.; Pastoriza-Santos, I.; Liz-Marzán, L.M.; Mulvaney, P. Gold nanorods: Synthesis, characterization and applications. Coord. Chem. Rev. 2005, 249, 1870–1901. [Google Scholar] [CrossRef]
- Vartia, O.S.; Ylä-Oijala, P.; Markkanen, J.; Puupponen, S.; Seppälä, A.; Sihvola, A.; Ala-Nissila, T. On the applicability of discrete dipole approximation for plasmonic particles. J. Quant. Spectrosc. Radiat. Transf. 2016, 169, 23–35. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Weinheim, Germany, 2008. [Google Scholar]
- Dombrovsky, L.A. Radiation Heat Transfer in Disperse Systems; Begell House: New York, NY, USA, 1996. [Google Scholar]
- Dombrovsky, L.A.; Baillis, D. Thermal Radiation in Disperse Systems: An Engineering Approach; Begell House: New York, NY, USA, 2010. [Google Scholar]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Multiple Scattering of Light by Particles: Radiative Transfer and Coherent Backscattering; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Van de Hulst, H.C. Light Scattering by Small Particles; Wiley: New York, NY, USA, 1957. [Google Scholar]
- McPeak, K.M.; Jayanti, S.V.; Kress, S.J.; Meyer, S.; Iotti, S.; Rossinelli, A.; Norris, D.J. Plasmonic films can easily be better: Rules and recipes. ACS Photonics 2015, 2, 326–333. [Google Scholar] [CrossRef] [PubMed]
- Vollmer, M.; Kreibig, U. Optical Properties of Metal Clusters; Springer: Berlin/Heidelberg, Germany, 1995; Volume 25, pp. 13–201. [Google Scholar]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl. Opt. 1985, 24, 4493–4499. [Google Scholar] [CrossRef] [PubMed]
- Novo, C.; Gomez, D.; Perez-Juste, J.; Zhang, Z.; Petrova, H.; Reismann, M.; Mulvaney, P.; Hartland, G.V. Contributions from radiation damping and surface scattering to the linewidth of the longitudinal plasmon band of gold nanorods: A single particle study. PCCP 2006, 8, 3540–3546. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Gao, B.-C.; Wiscombe, W.J.; Mishchenko, M.I.; Platnick, S.E.; Huang, H.-L.; Baum, B.A.; Hu, Y.X.; Winker, D.M.; Tsay, S.-C. Inherent and apparent scattering properties of coated or uncoated spheres embedded in an absorbing host medium. Appl. Opt. 2002, 41, 2740–2759. [Google Scholar] [CrossRef] [PubMed]
- Hinterwirth, H.; Wiedmer, S.K.; Moilanen, M.; Lehner, A.; Allmaier, G.; Waitz, T.; Lindner, W.; Lämmerhofer, M. Comparative method evaluation for size and size-distribution analysis of gold nanoparticles. J. Sep. Sci. 2013, 36, 2952–2961. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, E. Assemblies of Gold Nanoparticles at Liquid-Liquid Interfaces: From Liquid Optics to Electrocatalysis; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Devaty, R.; Sievers, A. Possibility of observing quantum size effects in the electromagnetic absorption spectrum of small metal particles. Phys. Rev. B 1985, 32, 1951–1954. [Google Scholar] [CrossRef]
- Perenboom, J.A.A.J.; Wyder, P.; Meier, F. Electronic properties of small metallic particles. Phys. Rep. 1981, 78, 173–292. [Google Scholar] [CrossRef] [Green Version]
- Pissuwan, D.; Valenzuela, S.M.; Miller, C.M.; Killingsworth, M.C.; Cortie, M.B. Destruction and control of toxoplasmagondii tachyzoites using gold nanosphere/antibody conjugates. Small 2009, 5, 1030–1034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jain, P.K.; Lee, K.S.; El-Sayed, I.H.; El-Sayed, M.A. Calculated absorption and scattering properties of gold nanoparticles of different size, shape, and composition: Applications in biological imaging and biomedicine. J. Phys. Chem. B 2006, 110, 7238–7248. [Google Scholar] [CrossRef] [PubMed]
- Yurkin, M.A.; Hoekstra, A.G. The discrete dipole approximation: An overview and recent developments. J. Quant. Spectrosc. Radiat. Transf. 2007, 106, 558–589. [Google Scholar] [CrossRef] [Green Version]
- Hewakuruppu, Y.L.; Dombrovsky, L.A.; Chen, C.; Timchenko, V.; Jiang, X.; Baek, S.; Taylor, R.A. Plasmonic “pump–probe” method to study semi-transparent nanofluids. Appl. Opt. 2013, 52, 6041–6050. [Google Scholar] [CrossRef] [PubMed]











| Sample | Concentration (GNRs/mL) | Volume Fraction |
|---|---|---|
| A | 0 | 0 |
| B | ||
| C | ||
| D | ||
| E | ||
| F |
| Sample | Absorbance | Temperature Increase (K) | Error of Temperature Measurements (K) |
|---|---|---|---|
| D | 0.61 | 0.2 | +0.015 |
| E | 0.80 | 0.4 | −0.014 |
| F | 0.96 | 0.5 | −0.013 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, X.; Timchenko, V.; Heng Yeoh, G.; Dombrovsky, L.; Taylor, R. The Effect of Gold Nanorods Clustering on Near-Infrared Radiation Absorption. Appl. Sci. 2018, 8, 1132. https://doi.org/10.3390/app8071132
Gu X, Timchenko V, Heng Yeoh G, Dombrovsky L, Taylor R. The Effect of Gold Nanorods Clustering on Near-Infrared Radiation Absorption. Applied Sciences. 2018; 8(7):1132. https://doi.org/10.3390/app8071132
Chicago/Turabian StyleGu, Xi, Victoria Timchenko, Guan Heng Yeoh, Leonid Dombrovsky, and Robert Taylor. 2018. "The Effect of Gold Nanorods Clustering on Near-Infrared Radiation Absorption" Applied Sciences 8, no. 7: 1132. https://doi.org/10.3390/app8071132
APA StyleGu, X., Timchenko, V., Heng Yeoh, G., Dombrovsky, L., & Taylor, R. (2018). The Effect of Gold Nanorods Clustering on Near-Infrared Radiation Absorption. Applied Sciences, 8(7), 1132. https://doi.org/10.3390/app8071132