Bond Fatigue of TRC with Epoxy Impregnated Carbon Textiles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Samples
2.3. Test Setup
2.4. Load Regime and Experimental Program
3. Results
3.1. Reference Tests
3.2. Cyclic Stress–Strain Behavior
3.3. Development of Deformation
3.3.1. General Remarks
3.3.2. Dependence on Load Level
3.3.3. Dependence on Anchorage Length
3.4. Development of Stiffness
3.4.1. General Remarks
3.4.2. Dependence on Load Level
3.4.3. Dependence on Anchorage Length
3.5. S-N Diagram
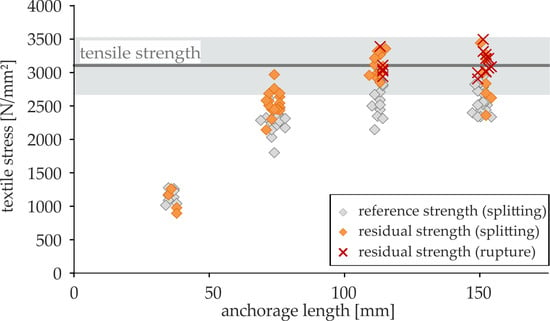
3.6. Residual Strength
4. Summary, Conclusions, and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Materials
| Longitudinal | Transversal | ||
|---|---|---|---|
| Fiber strand distance | [mm] | 38 | 38 |
| Cross-section of the strand | [mm2] | 3.62 | 3.62 |
| Average tensile strength | [N/mm2] | 3200 | 3300 |
| Modulus of elasticity | [N/mm2] | >220000 | >205000 |
| Ingredients | Quantity [kg/m3] |
|---|---|
| Binder | 621 |
| Quartz fine sand | 250 |
| Sand 0/2 | 530 |
| Granite grit 2/5 | 837 |
| Super-plasticizer | 16 |
| Water | 145 |
Appendix B. Results








| Anchorage Length | Load Level σmin/σmax [%] | Number of Cycles to Failure | Residual Strength [N/mm2] | Anchorage Length | Load Level σmin/σmax [%] | Number of Cycles to Failure | Residual Strength [N/mm2] |
|---|---|---|---|---|---|---|---|
| 1a | 30/90 | 532 | - | 2a | 30/90 | 2009000 * | 2296 |
| 13801 | - | 2009000 * | 2567 | ||||
| 2009000 * | 1169 | 2009000 * | 2677 | ||||
| 30/95 | 39 | - | 2009000 * | 2629 | |||
| 42 | - | 30/95 | 2009000 * | 2447 | |||
| 50/70 | 2009000 * | 976 | 2009000 * | 2753 | |||
| 2009000 | 895 | 2009000 * | 2961 | ||||
| 50/85 | 5865 | - | 50/70 | 2009000 * | 2501 | ||
| 2009000 * | 1259 | 2009000 * | 2536 | ||||
| 50/90 | 2 | - | 2009000 * | 2478 | |||
| 28112 | - | 2009000 * | 2429 | ||||
| 34323 | - | 50/85 | 5308 | - | |||
| 3a | 30/90 | 41078 | - | 2009000 * | 2683 | ||
| 57733 | - | 2009000 * | 2449 | ||||
| 2009000 * | 2965 | 2009000 * | 2447 | ||||
| 2009000 * | 3379 | 50/90 | 2009000 * | 2137 | |||
| 30/95 | 378 | 2009000 * | 2443 | ||||
| 2009000 * | 3083 | 2009000 * | 2576 | ||||
| 2009000 * | 3326 | 4a | 30/90 | 2009000 * | 2897 | ||
| 2009000 * | 2844 | 2009000 * | 3000 | ||||
| 50/70 | 2009000 * | 3015 | 2009000 * | 3433 | |||
| 2009000 * | 2930 | 2009000 * | 3306 | ||||
| 2009000 * | 3101 | 30/95 | 328198 | - | |||
| 2009000 * | 2944 | 2009000 * | 3262 | ||||
| 50/85 | 2009000 * | 3107 | 2009000 * | 3201 | |||
| 2009000 * | 3039 | 2009000 * | 2990 | ||||
| 2009000 * | 2964 | 50/70 | 2009000 * | 2353 | |||
| 2009000 * | 3257 | 2009000 * | 2828 | ||||
| 50/90 | 2009000 * | 3311 | 2009000 * | 2683 | |||
| 2009000 * | 2949 | 2009000 * | 3197 | ||||
| 2009000 * | 3206 | 50/85 | 2009000 * | 3057 | |||
| 2009000 * | 3348 | 2009000 * | 3007 | ||||
| 2009000 * | 2615 | ||||||
| 2009000 * | 3261 | ||||||
| 50/90 | 2009000 * | 2994 | |||||
| 2009000 * | 3204 | ||||||
| 2009000 * | 3077 | ||||||
| 2009000 * | 3485 |
References
- Scheerer, S.; Chudoba, R.; Garibaldi, M.P.; Curbach, M. Shells made of Textile Reinforced Concrete—Applications in Germany. J. Int. Assoc. Shell Spat. Struct. JIASS 2017, 58, 79–93. [Google Scholar] [CrossRef]
- Curbach, M.; Graf, W.; Jesse, D.; Sickert, J.-U.; Weiland, S. Segmentbrücke aus textilbewehrtem Beton—Konstruktion, Fertigung, numerische Berechnung. Beton-und Stahlbetonbau 2007, 102, 342–352. [Google Scholar] [CrossRef]
- Michler, H. Segmentbrücke aus textilbewehrtem Beton—Rottachsteg Kempten im Allgäu. Beton-und Stahlbetonbau 2013, 108, 325–334. [Google Scholar] [CrossRef]
- Kulas, C.; Goralski, K. Die weltweit längste Textilbetonbrücke—Technische Details und Praxiserfahrungen. Beton-und Stahlbetonbau 2014, 109, 812–817. [Google Scholar] [CrossRef]
- Rempel, S.; Hegger, J.; Kulas, C. A pedestrian bridge made of textile reinforced concrete. In Proceedings of the 16th European Bridge Conference, Endinburgh, UK, 23–25 June 2015. [Google Scholar]
- Helbig, T.; Rempel, S.; Unterer, K.; Kulas, C.; Hegger, J. Fuß- und Radwegbrücke aus Carbonbeton in Albstadt-Ebingen—Die weltweit erste ausschließlich carbonfaserbewehrte Betonbrücke. Beton-und Stahlbetonbau 2016, 111, 676–685. [Google Scholar] [CrossRef]
- Rempel, S.; Kulas, C.; Will, N.; Bielak, J. Extremely Light and Slender Precast Pedestrian-Bridge Made Out of Textile-Reinforced Concrete (TRC). In Proceedings of the fib Symposium, Maastricht, The Netherlands, 12–14 June 2017. [Google Scholar] [CrossRef]
- Rempel, S. Erste Straßenbrücke aus Carbonbeton. In Proceedings of the 9th Carbon- und Textilbetontage, Dresden, Germany, 26–27 September 2017. [Google Scholar]
- Bielak, J.; Bergmann, S.; Hegger, J. Querkrafttragfähigkeit von Carbonbeton-Plattenbrücken mit C-förmiger Querkraftbewehrung—Theoretische und experimentelle Untersuchungen für zwei Straßenbrücken in Gaggenau. Beton-und Stahlbetonbau 2019, 114. [Google Scholar] [CrossRef]
- Homepage of the Project Carbon Concrete Composite. Available online: www.bauen-neu-denken.de (accessed on 21 March 2019).
- Jesse, F. Ermüdet Textilbeton? Verhalten unter nicht-ruhender Beanspruchung. In Proceedings of the 4th Anwendertagung Textilbeton, Dresden, Germany, 27–28 September 2012. [Google Scholar]
- Feix, J.; Hansl, M. Pilotanwendungen von Textilbeton für Verstärkungen im Brückenbau. In Proceedings of the 25th Dresdner Brückenbausymposium, Dresden, Germany, 9–10 March 2015; Curbach, M., Ed.; pp. 99–110. [Google Scholar]
- Schütze, E.; Lorenz, E.; Curbach, M. Static and Dynamic Fatigue Strength of Textile Reinforced Concrete. In Proceedings of the IABSE Conference, Nara, Japan, 13–15 May 2015; IABSE, Ed.; pp. 332–333. [Google Scholar]
- Holz, K.; Schütze, E.; Garibaldi, P.; Curbach, M. Determination of Material Properties of TRC under Cyclic Loads. ACI Spec. Publ. SP-ACI 549-01 2018, 324, 1–16. [Google Scholar]
- De Munck, M.; Tysmans, T.; Wastiels, J.; Kapsalis, P.; Vervloet, J.; El Kadi, M.; Remy, O. Fatigue Behaviour of Textile Reinforced Cementitious Composites and Their Application in Sandwich Elements. Appl. Sci. 2019, 9, 1293. [Google Scholar] [CrossRef]
- Wagner, J.; Holz, K.; Curbach, M. Zyklische Verbundversuche mit Carbonbeton. Beton-und Stahlbetonbau 2018, 113, 525–534. [Google Scholar] [CrossRef]
- Wagner, J.; Curbach, M. Tensile load bearing and Bond Behaviour of Carbon Reinforced Concrete under cyclic Loading. In Proceedings of the fib Congress, Melbourne, Australia, 7–11 October 2018; Foster, S., Gilbert, R., Mendis, P., Al-Mahaidi, R., Millar, D., Eds.; [Google Scholar]
- Solidian GmbH. Technical Data Sheet Solidian GRID Q95/95-CCE-38. 2017. Available online: https://www.solidian.com/fileadmin/user_upload/pdf/TDS/solidian_GRID_Q95.95-CCE-38.pdf (accessed on 14 May 2019).
- Schneider, K.; Butler, M.; Mechtcherine, V. Carbon Concrete Composites C3—Nachhaltige Bindemittel und Betone für die Zukunft. Beton-und Stahlbetonbau 2017, 112, 784–794. [Google Scholar] [CrossRef]
- DIN EN 196-1. Prüfverfahren für Zement–Teil 1: Bestimmung der Festigkeit; Deutsche Fassung EN 196-1:2016; Beuth: Berlin, Germany, November 2016. [Google Scholar]
- Bielak, J.; Scholzen, A.; Chudoba, R.; Schütze, E.; Schmidt, J.; Reichel, S. Prüfempfehlung zur Verwendung in C3—Beidseitiger Textilauszugversuche/Double Sided Textile Pull-Out (DPO). In Ergebnisbericht Vorhaben B3—Konstruktionsgrundsätze, Sicherheits-und Bemessungskonzepte sowie standardisierte Prüfmethoden für Carbonbeton; Research Report; TU Dresden: Dresden, Germany, 2016. [Google Scholar]
- Bielak, J.; Li, Y.; Hegger, J.; Chudoba, R. Numerical and Experimental Characterization of Anchorage Length for Textile Reinforced Concrete. In RILEM Bookseries 15, Proceedings of Strain-Hardening Cement-Based Composites (SHCC4), Dresden, Germany, 18–20 September 2017; Mechtcherine, V., Slowik, V., Kabele, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 409–417. [Google Scholar]
- Schütze, E.; Bielak, J.; Scheerer, S.; Hegger, J.; Curbach, M. Einaxialer Zugversuch für Carbonbeton mit textiler Bewehrung/Uniaxial tensile test for carbon reinforced concrete with textile reinforcement. Beton-und Stahlbetonbau 2018, 113, 33–47. [Google Scholar] [CrossRef]
- Klausen, D. Festigkeit und Schädigung von Beton bei häufig wiederholter Beanspruchung. Ph.D. Dissertation, TU Darmstadt, Darmstadt, Germany, 1978. [Google Scholar]
- Balázs, G.L. Deformation based fatigue failure criterion. In, Localized Damage III—Computer-Aided Assessment and Control; Aliabadi, M.H., Carbinteri, A., Kaliszky, S., Cart-Wright, D.J., Eds.; Computational Mechanics Publications: Southampton, UK, 1994; pp. 631–638. [Google Scholar]
- Holmen, J.O. Fatigue of Concrete by Constant and Variable Amplitude Loading. Ph.D. Dissertation, University of Trondheim, Norwegian Institute of Technology, Division of Concrete Structures, Trondheim, Norway, 1979. [Google Scholar]
- Oneschkow, N. Analyse des Ermüdungsverhaltens von Beton anhand der Dehnungsentwicklung, 2nd ed.; Berichte aus dem Institut für Baustoffe, Heft 13; Institut für Baustoffe, Leibniz Universität Hannover: Hannover, Germany, 2016. [Google Scholar]
- Schütze, E.; Curbach, M. Zur experimentellen Charakterisierung des Verbundverhaltens von Carbonbeton mit Spalten als maßgeblichem Versagensmechanismus. Bauingenieur 2019, 94, 133–141. [Google Scholar]
- Lorenz, E. Endverankerung und Übergreifung textiler Bewehrungen in Betonmatrices. Ph.D. Dissertation, TU Dresden, Dresden, Germany, 2014. [Google Scholar]
















| Anchorage Length | Number of Tested (Evaluated *) Specimens at Load Level σmin/σmax [%] | ||||
|---|---|---|---|---|---|
| 30/90 | 30/95 | 50/70 | 50/85 | 50/90 | |
| 1a | 4 (3) | 4 (2) | 4 (2) | 4 (2) | 4 (3) |
| 2a | 4 | 4 (3) | 4 | 4 | 4 (3) |
| 3a | 4 | 4 | 4 | 4 | 4 |
| 4a | 4 | 4 | 4 | 4 | 4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wagner, J.; Curbach, M. Bond Fatigue of TRC with Epoxy Impregnated Carbon Textiles. Appl. Sci. 2019, 9, 1980. https://doi.org/10.3390/app9101980
Wagner J, Curbach M. Bond Fatigue of TRC with Epoxy Impregnated Carbon Textiles. Applied Sciences. 2019; 9(10):1980. https://doi.org/10.3390/app9101980
Chicago/Turabian StyleWagner, Juliane, and Manfred Curbach. 2019. "Bond Fatigue of TRC with Epoxy Impregnated Carbon Textiles" Applied Sciences 9, no. 10: 1980. https://doi.org/10.3390/app9101980
APA StyleWagner, J., & Curbach, M. (2019). Bond Fatigue of TRC with Epoxy Impregnated Carbon Textiles. Applied Sciences, 9(10), 1980. https://doi.org/10.3390/app9101980