Enhancing the Viscoelastic Performance of Carbon Fiber Composites by Incorporating CNTs and ZnO Nanofillers
Abstract
:1. Introduction
2. Synthesis
2.1. Nanofillers Deposition
2.2. Composites Preparation
3. DMA Analysis and Thermal Activation Energy Calculation
4. Results and Discussion
4.1. Temperature Sweep
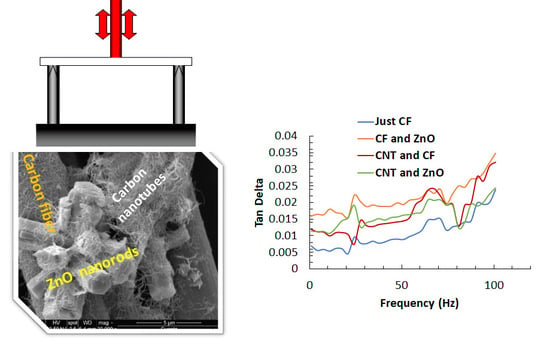
4.2. Frequency Sweep
4.3. Effect of Frequency on Glass Transition Temperature
4.4. Calculation of Thermal Activation Energy (ΔH)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Siochi, E.J.; Harrison, J.S. Structural nanocomposites for aerospace applications. MRS Bull. 2015, 40, 829–835. [Google Scholar] [CrossRef] [Green Version]
- Fitzer, E. Technical Status and Future Prospects of Carbon Fibres and their Application in Composites with Polymer Matrix (CFRPs); Springe: Berlin, Germany, 1985; pp. 3–45. [Google Scholar]
- Raja, S.; Prathap, G.; Sinha, P.K. Active vibration control of composite sandwich beams with piezoelectric extension-bending and shear actuators. Smart Mater. Struct. 2002, 11, 63–71. [Google Scholar] [CrossRef]
- Gibson, R.F.; Chen, Y.; Zhao, H. Improvement of Vibration Damping Capacity and Fracture Toughness in Composite Laminates by the Use of Polymeric Interleaves. J. Eng. Mater. Technol. 2001, 123, 309–314. [Google Scholar] [CrossRef]
- Kuttner, C.; Hanisch, A.; Schmalz, H.; Eder, M.; Schlaad, H.; Burgert, I.; Fery, A. Influence of the Polymeric Interphase Design on the Interfacial Properties of (Fiber-Reinforced) Composites. ACS Appl. Mater. Interfaces 2013, 5, 2469–2478. [Google Scholar] [CrossRef] [PubMed]
- Hudnut, S.W.; Chung, D.D.L. Use of submicron diameter carbon filaments for reinforcement between continuous carbon fiber layers in a polymer-matrix composite. Carbon 1995, 33, 1627–1631. [Google Scholar] [CrossRef]
- Dutra, R.C.L.; Soares, B.G.; Campos, E.A.; Silva, J.L.G. Hybrid composites based on polypropylene and carbon fiber and epoxy matrix. Polymer 2000, 41, 3841–3849. [Google Scholar] [CrossRef]
- Gan, Y.X. Effect of Interface Structure on Mechanical Properties of Advanced Composite Materials. Int. J. Mol. Sci. 2009, 10, 5115–5134. [Google Scholar] [CrossRef] [PubMed]
- Saito, R.; Dresselhaus, G.; Dresselhaus, M.S. Physical Properties of Carbon Nanotubes; Imperial College Press: London, UK, 1998. [Google Scholar]
- Thostenson, E.T.; Ren, Z.; Chou, T.-W. Advances in the science and technology of carbon nanotubes and their composites: A review. Compos. Sci. Technol. 2001, 61, 1899–1912. [Google Scholar] [CrossRef]
- Terrones, M. Science and Technology of the Twenty-First Century: Synthesis, Properties, and Applications of Carbon Nanotubes. Ann. Rev. Mater. Res. 2003, 33, 419–501. [Google Scholar] [CrossRef]
- Sinnott, S.B.; Andrews, R. Carbon Nanotubes: Synthesis, Properties, and Applications. Crit. Rev. Solid State Mater. Sci. 2001, 26, 145–249. [Google Scholar] [CrossRef]
- Thanh, Q.N.; Jeong, H.; Kim, J.; Kevek, J.W.; Ahn, Y.H.; Lee, S.; Minot, E.D.; Park, J.Y. Transfer-Printing of As-Fabricated Carbon Nanotube Devices onto Various Substrates. Adv. Mater. 2012, 24, 4499–4504. [Google Scholar] [CrossRef] [PubMed]
- Baughman, R.H.; Zakhidov, A.A.; de Heer, W.A. Carbon Nanotubes—The Route Toward Applications. Science 2002, 297, 787–792. [Google Scholar] [CrossRef] [PubMed]
- Siddiqui, N.A.; Li, E.L.; Sham, M.L.; Tang, B.Z.; Gao, S.L.; Mäder, E.; Kim, J.K. Tensile strength of glass fibres with carbon nanotube–epoxy nanocomposite coating: Effects of CNT morphology and dispersion state. Compos. Part A Appl. Sci. Manuf. 2010, 41, 539–548. [Google Scholar] [CrossRef]
- Tehrani, M.; Safdari, M.; Al-Haik, M.S. Nanocharacterization of creep behavior of multiwall carbon nanotubes/epoxy nanocomposite. Int. J. Plast. 2011, 27, 887–901. [Google Scholar] [CrossRef]
- Soliman, E.; Al-Haik, M.; Taha, M.R. On and off-axis tension behavior of fiber reinforced polymer composites incorporating multi-walled carbon nanotubes. J. Compos. Mater. 2012, 46, 1661–1675. [Google Scholar] [CrossRef]
- Tehrani, M.; Boroujeni, A.Y.; Hartman, T.B.; Haugh, T.P.; Case, S.W.; Al-Haik, M.S. Mechanical characterization and impact damage assessment of a woven carbon fiber reinforced carbon nanotube–epoxy composite. Compos. Sci. Technol. 2013, 75, 42–48. [Google Scholar] [CrossRef]
- Abdelal, N.R.; Al-Saleh, M.H.; Irshidat, M.R. Utilizing Vacuum Bagging Process to Prepare Carbon Fiber/CNT-Modified-epoxy Composites with Improved Mechanical Properties. Polym.-Plast. Technol. Eng. 2018, 57, 175–184. [Google Scholar] [CrossRef]
- Johannesson, T.; Sjöblom, P.; Seldén, R. The detailed structure of delamination fracture surfaces in graphite/epoxy laminates. J. Mater. Sci. 1984, 19, 1171–1177. [Google Scholar] [CrossRef]
- Van Hooijdonk, E.; Bittencourt, C.; Snyders, R.; Colomer, J.F. Functionalization of vertically aligned carbon nanotubes. Beilstein J. Nanotechnol. 2013, 4, 129–152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suhr, J.; Koratkar, N.; Keblinski, P.; Ajayan, P. Viscoelasticity in carbon nanotube composites. Nat. Mater. 2005, 4, 134–137. [Google Scholar] [CrossRef]
- Koratkar, N. Multifunctional structural reinforcement featuring carbon nanotube films. Compos. Sci. Technol. 2003, 63, 1525–1531. [Google Scholar] [CrossRef]
- Zhou, X.; Shin, E.; Wang, K.W.; Bakis, C.E. Interfacial damping characteristics of carbon nanotube-based composites. Compos. Sci. Technol. 2004, 64, 2425–2437. [Google Scholar] [CrossRef]
- Fu, Y.Q.; Luo, J.K.; Du, X.Y.; Flewitt, A.J.; Li, Y.; Markx, G.H.; Walton, A.J.; Milne, W.I. Recent developments on ZnO films for acoustic wave based bio-sensing and microfluidic applications: A review. Sens. Actuators B Chem. 2010, 143, 606–619. [Google Scholar] [CrossRef]
- Li, L.; Yang, H.; Yu, J.; Chen, Y.; Ma, J.; Zhang, J.; Song, Y.; Gao, F. Controllable growth of ZnO nanowires with different aspect ratios and microstructures and their photoluminescence and photosensitive properties. J. Cryst. Growth 2009, 311, 4199–4206. [Google Scholar] [CrossRef]
- Wang, Z.L. Zinc oxide nanostructures: Growth, properties and applications. J. Phys. Condens. Matter 2004, 16, R829–R858. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Y.; Kong, J.; Jia, H.; Wang, Z. Synthesis of ZnO nanosheets via electrodeposition method and their optical properties, growth mechanism. Opt. Mater. 2015, 46, 179–185. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, H.; Zhao, B.; Bao, X. Size control of ZnO nanoparticles via thermal decomposition of zinc acetate coated on organic additives. J. Cryst. Growth 2004, 263, 447–453. [Google Scholar] [CrossRef]
- Khan, M.F.; Ansari, A.H.; Hameedullah, M.; Ahmad, E.; Husain, F.M.; Zia, Q.; Baig, U.; Zaheer, M.R.; Alam, M.M.; Khan, A.M.; et al. Sol-gel synthesis of thorn-like ZnO nanoparticles endorsing mechanical stirring effect and their antimicrobial activities: Potential role as nano-antibiotics. Sci. Rep. 2016, 6, 27689. [Google Scholar] [CrossRef]
- Chang, P.C.; Fan, Z.; Wang, D.; Tseng, W.Y.; Chiou, W.A.; Hong, J.; Lu, J.G. ZnO Nanowires Synthesized by Vapor Trapping CVD Method. Chem. Mater. 2004, 16, 5133–5137. [Google Scholar] [CrossRef]
- Lyu, S.C.; Zhang, Y.; Ruh, H.; Lee, H.J.; Shim, H.W.; Suh, E.K.; Lee, C.J. Low temperature growth and photoluminescence of well-aligned zinc oxide nanowires. Chem. Phys. Lett. 2002, 363, 134–138. [Google Scholar] [CrossRef]
- Wu, J.J.; Liu, S.C. Low-Temperature Growth of Well-Aligned ZnO Nanorods by Chemical Vapor Deposition. Adv. Mater. 2002, 14, 215–218. [Google Scholar] [CrossRef]
- Akgun, M.C.; Kalay, Y.E.; Unalan, H.E. Hydrothermal zinc oxide nanowire growth using zinc acetate dihydrate salt. J. Mater. Res. 2012, 27, 1445–1451. [Google Scholar] [CrossRef]
- Lin, Y.; Ehlert, G.; Sodano, H.A. Increased Interface Strength in Carbon Fiber Composites through a ZnO Nanowire Interphase. Adv. Funct. Mater. 2009, 19, 2654–2660. [Google Scholar] [CrossRef]
- Demes, T.; Ternon, C.; Riassetto, D.; Stambouli, V.; Langlet, M. Comprehensive study of hydrothermally grown ZnO nanowires. J. Mater. Sci. 2016, 51, 10652–10661. [Google Scholar] [CrossRef]
- Ghosh, S.; Gomathi, A.; Rao, C.N.R. Stable Dispersions of Metal Oxide Nanowires and Nanoparticles in Water, Dimethylformamide and Toluene. J. Nanosci. Nanotechnol. 2009, 9, 5214–5222. [Google Scholar] [CrossRef] [PubMed]
- Hung, C.H.; Whang, W.T. A novel low-temperature growth and characterization of single crystal ZnO nanorods. Mater. Chem. Phys. 2003, 82, 705–710. [Google Scholar] [CrossRef]
- Tak, Y.; Yong, K.J. Controlled growth of well-aligned ZnO nanorod array using a novel solution method. J. Phys. Chem. B 2005, 109, 19263–19269. [Google Scholar] [CrossRef] [PubMed]
- Strano, V.; Urso, R.G.; Scuderi, M.; Iwu, K.O.; Simone, F.; Ciliberto, E.; Spinella, C.; Mirabella, S. Double Role of HMTA in ZnO Nanorods Grown by Chemical Bath Deposition. J. Phys. Chem. C 2014, 118, 28189–28195. [Google Scholar] [CrossRef]
- Alipour Skandani, A.; Masghouni, N.; Case, S.W.; Leo, D.J.; Al-Haik, M. Enhanced vibration damping of carbon fibers-ZnO nanorods hybrid composites. Appl. Phys. Lett. 2012, 101, 73111. [Google Scholar] [CrossRef] [Green Version]
- Goertzen, W.K.; Kessler, M.R. Dynamic mechanical analysis of carbon/epoxy composites for structural pipeline repair. Compos. Part B Eng. 2007, 38, 1–9. [Google Scholar] [CrossRef]
- Li, G.; Lee-Sullivan, P.; Thring, R.W. Determination of activation energy for glass transition of an epoxy adhesive using dynamic mechanical analysis. J. Therm. Anal. Calorim. 2000, 60, 377–390. [Google Scholar] [CrossRef]
- Flynn, J.H. Temperature dependence of the rate of reaction in thermal analysis;The Arrhenius equation in condensed phase kinetics. J. Therm. Anal. 1990, 36, 1579–1593. [Google Scholar] [CrossRef]
- Gray, V.; Whittaker, M. A Discussion of Non-Constant Creep Activation Energy. J. Mater. Sci. Eng. 2017, 6, 372. [Google Scholar]
- Weertman, J. Theory of Steady-State Creep Based on Dislocation Climb. J. Appl. Phys. 1955, 26, 1213–1217. [Google Scholar] [CrossRef]
- Ayyagari, S.; Al-Haik, M.; Rollin, V. Mechanical and Electrical Characterization of Carbon Fiber/Bucky Paper/Zinc Oxide Hybrid Composites. J. Carbon Res. 2018, 4, 6. [Google Scholar] [CrossRef]
- Al-Haik, M.S.; Hussaini, M.Y.; Garmestani, H. Prediction of nonlinear viscoelastic behavior of polymeric composites using an artificial neural network. Int. J. Plast. 2006, 22, 1367–1392. [Google Scholar] [CrossRef]
- Al-Haik, M.S.; Garmestani, H.; Savran, A. Explicit and implicit viscoplastic models for polymeric composite. Int. J. Plast. 2004, 20, 1875–1907. [Google Scholar] [CrossRef]
- Garmestani, H.; Al-Haik, M.S.; Dahmen, K.; Tannenbaum, R.; Li, D.; Sablin, S.S.; Hussaini, M.Y. Polymer-Mediated Alignment of Carbon Nanotubes under High Magnetic Fields. Adv. Mater. 2003, 15, 1918–1921. [Google Scholar] [CrossRef]
- ASTM Dynamic Mechanical Properties: Determination and Report of Procedures. In Standard Practice for Plastics; ASTM International: West Conshohocken, PA, USA, 2011.
- Pramanik, C.; Gissinger, J.R.; Kumar, S.; Heinz, H. Carbon Nanotube Dispersion in Solvents and Polymer Solutions: Mechanisms, Assembly, and Preferences. ACS Nano 2017, 11, 12805–12816. [Google Scholar] [CrossRef]
- Chartoff, R.P.; Menczel, J.D.; Dillman, S.H. Dynamic Mechanical Analysis. In Thermal Analysis of Polymers: Fundamentals and Applications; Menczel, J.D., Prime, R.B., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Allaoui, A.; Bounia, N.E. How carbon nanotubes affect the cure kinetics and glass transition temperature of their epoxy composites? A review. eXPRESS Polym. Lett. 2009, 3, 588–594. [Google Scholar] [CrossRef]








| Configuration | Loss Modulus Peak (Tg) in °C | Tan Delta Peak (Tg) in °C | Difference % |
|---|---|---|---|
| Just CF | 73.37 | 77.2 | 5 |
| CF and ZnO | 73.28 | 79.33 | 7.6 |
| CNT and CF | 71.5 | 76.88 | 7.0 |
| CNT and ZnO | 72.77 | 82.06 | 11.3 |
| Configuration | Change in Tan Delta (Peak Values, %) | Change in Loss Modulus (Peak Values, %) | Change in Storage Modulus (at 60 °C, %) |
|---|---|---|---|
| CF and ZnO | 10.04 | −18.26 | −25.95 |
| CNT and CF | −9.82 | −25 | −26.44 |
| CNT and ZnO | 10.98 | 15.53 | 25.51 |
| Configuration | Change in Tan Delta (at 61 Hz, %) | Change in Loss Modulus (at 61 Hz, %) | Change in Storage Modulus (at 61 Hz, %) |
|---|---|---|---|
| CF and ZnO | 84.88 | 54.15 | −16.62 |
| CNT and CF | 77.98 | 68.68 | −5.22 |
| CNT and ZnO | 47.69 | 32.45 | −10.32 |
| Configuration | ΔH from tanδ Peaks (kJ/mol) | ΔH from Loss Modulus Peaks (kJ/mol) |
|---|---|---|
| Just CF | 0.85 | 0.83 |
| CF and ZnO | 0.86 | 0.80 |
| CF and CNTs | 0.96 | 0.88 |
| CNTs and ZnO | 0.87 | 0.84 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayyagari, S.; Al-Haik, M. Enhancing the Viscoelastic Performance of Carbon Fiber Composites by Incorporating CNTs and ZnO Nanofillers. Appl. Sci. 2019, 9, 2281. https://doi.org/10.3390/app9112281
Ayyagari S, Al-Haik M. Enhancing the Viscoelastic Performance of Carbon Fiber Composites by Incorporating CNTs and ZnO Nanofillers. Applied Sciences. 2019; 9(11):2281. https://doi.org/10.3390/app9112281
Chicago/Turabian StyleAyyagari, Suma, and Marwan Al-Haik. 2019. "Enhancing the Viscoelastic Performance of Carbon Fiber Composites by Incorporating CNTs and ZnO Nanofillers" Applied Sciences 9, no. 11: 2281. https://doi.org/10.3390/app9112281
APA StyleAyyagari, S., & Al-Haik, M. (2019). Enhancing the Viscoelastic Performance of Carbon Fiber Composites by Incorporating CNTs and ZnO Nanofillers. Applied Sciences, 9(11), 2281. https://doi.org/10.3390/app9112281