A Self-Consistent Quantum Field Theory for Random Lasing
Abstract
:1. Introduction
2. Quantum-Field Theory for Photonic Transport
2.1. Nonlinear Response
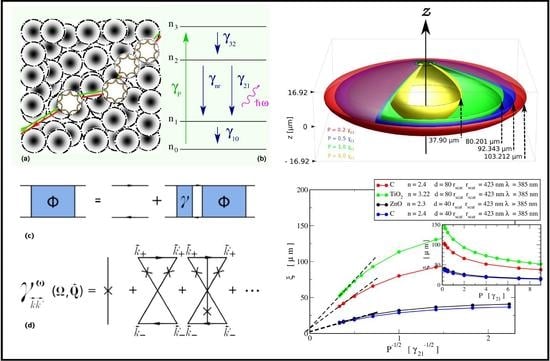
2.2. Bethe-Salpeter Equation for Photonic Transport in Samples of Disordered Active Mie Resonators
2.3. Coupling to the Four Level Laser Rate Equations for Quantum Cascades
3. Results and Discussion
3.1. The Coherence Volume of D = 3 Dimensional Random Lasers
3.2. Scattering mean-free Path and Diffusion Coefficient at the Random Laser Threshold
3.3. Material-Dependency of the Mie Characteristics in Multiple Scattering Random Lasers
3.4. Power Law Behavior of the Correlation Length Scale in Stationary State
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cao, H.; Zhao, Y.G.; Ho, S.T.; Seelig, E.W.; Wang, Q.H.; Chang, R.P.H. Random laser action in semiconductor powder. Phys. Rev. Lett. 1999, 82, 2278–2281. [Google Scholar] [CrossRef]
- Cao, H. Lasing in random media. Waves Random Media 2003, 13, R1–R39. [Google Scholar] [CrossRef]
- Dice, G.D.; Mujumdar, S.; Elezzabi, A.Y. Plasmonically enhanced diffusive and subdiffusive metal nanoparticle-dye random laser. Appl. Phys. Lett. 2005, 86, 131105. [Google Scholar] [CrossRef]
- Wiersma, D. The physics and applications of random lasers. Nat. Phys. 2008, 4, 359–367. [Google Scholar] [CrossRef]
- Noginov, M.A.; Zhu, G.; Belgrave, A.M.; Bakker, R.; Shalaev, V.M.; Narimanov, E.E.; Stout, S.; Herz, E.; Suteewong, T.; Wiesner, U. Demonstration of a spaser-based nanolaser. Nature 2009, 460, 1110–1112. [Google Scholar] [CrossRef] [PubMed]
- Polson, R.C.; Vardeny, Z.V. Spatially mapping random lasing cavities. Opt. Lett. 2010, 35, 2801. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, A.K.; Mujumdar, S. Random Lasing over Gap States from a Quasi-One-Dimensional Amplifying Periodic-on-Average Random Superlattice. Phys. Rev. Lett. 2013, 111, 233903. [Google Scholar] [CrossRef]
- Uppu, R.; Mujumdar, S. Exponentially Tempered Lévy Sums in Random Lasers. Phys. Rev. Lett. 2015, 114, 183903. [Google Scholar] [CrossRef]
- Niyuki, R.; Fujiwara, H.; Nakamura, T.; Ishikawa, Y.; Koshizaki, N.; Tsuji, T.; Sasaki, K. Double threshold behavior in a resonance-controlled ZnO random laser. APL Photonics 2014, 2, 036101. [Google Scholar] [CrossRef]
- Shi, X.; Liao, Y.-M.; Lin, H.-Y.; Tsao, P.-W.; Wu, M.-J.; Lin, S.-Y.; Hu, H.-H.; Wang, Z.; Lin, T.-Y.; Lai, Y.-C.; et al. Dissolvable and Recyclable Random Lasers. ACS Nano 2017, 11, 7600–7607. [Google Scholar] [CrossRef]
- Safdas, A.; Wang, Y.; Krauss, T.F. Random lasing in uniform perovskite thin films. Opt. Express 2018, 26, A75–A80. [Google Scholar] [CrossRef] [PubMed]
- Lau, S.-P.; Yang, H.; Yu, S.F.; Yuen, C.; Leong, E.S.P.; Li, H.; Hng, H.H. Flexible Ultraviolet Random Lasers Based on Nanoparticles. Small 2005, 1, 956–959. [Google Scholar] [CrossRef] [PubMed]
- Vasileva, E.L.; Li, Y.U.; Sychugov, I.; Mensied, M.; Berglund, L.; Popov, S. Lasing from organic dye molecules embedded in transparent wood. Adv. Opt. Mater. 2017, 5, 1700057. [Google Scholar] [CrossRef]
- Oivurova, M.A.K.; Vasileva, E.L.; Li, Y.U.; Berglund, L.; Popov, S. Complete spatial coherence characterization of quasi-random laser emission from dye doped transparent wood. Opt. Express 2018, 26, 13476. [Google Scholar]
- Hackenbroich, G.; Viviescas, C.; Haake, F. Field quantization for chaotic resonators with overlapping modes. Phys. Rev. Lett. 2002, 89, 083902. [Google Scholar] [CrossRef] [PubMed]
- Mujumdar, S.; Ricci, M.; Torre, R.; Wiersma, D.S. Amplified Extended Modes in Random Lasers. Phys. Rev. Lett. 2004, 93, 053903. [Google Scholar] [CrossRef]
- Hackenbroich, G. Statistical theory of multimode random lasers. J. Phys. A Math. Gen. 2005, 38, 10537. [Google Scholar] [CrossRef]
- Mujumdar, D.; Türck, V.; Torre, R.; Wiersma, D.S. Chaotic behavior of a random laser with static disorder. Phys. Rev. A 2007, 76, 033807. [Google Scholar] [CrossRef] [Green Version]
- Lepri, S. Fluctuations in a Diffusive Medium with Gain. Phys. Rev. Lett. 2013, 110, 230603. [Google Scholar] [CrossRef] [Green Version]
- Höfner, W.; Wünsche, H.-J.; Henneberger, F. A random laser as a dynamical network. New J. Phys. 2014, 16, 033002. [Google Scholar] [CrossRef] [Green Version]
- Lepri, S.; Trono, C.; Giacomelli, G. Complex Active Optical Networks as a New Laser Concept. Phys. Rev. Lett. 2017, 118, 12390. [Google Scholar] [CrossRef]
- Gaio, M.; Saxena, D.; Bertolotti, J.; Pisignano, D.; Camposeo, A.; Sapienza, R. A nanophotonic laser on a graph. Nat. Commun. 2019, 10, 226. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Soukoulis, C.M. Time Dependent Theory for Random Laser. Phys. Rev. Lett. 2002, 85, 70–73. [Google Scholar] [CrossRef] [PubMed]
- Soukoulis, C.M.; Jiang, X.; Xu, J.Y.; Cao, H. Dynamic response and relaxation oscillations in random lasers. Phys. Rev. B 2002, 65, 041103R. [Google Scholar] [CrossRef]
- Türeci, H.E.; Stone, A.D.; Collier, B. Self-consistent multi-mode lasing theory for complex or random lasing media. Phys. Rev. A 2006, 74, 043822. [Google Scholar] [CrossRef]
- Türeci, H.E.; Ge, L.; Rotter, S.; Stone, A.D. Strong Interactions in Multimode Random Lasers. Science 2008, 320, 643–646. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Conti, C.; Fratalocchi, A. Dynamic light diffusion, Anderson localization and lasing in disordered inverted opals: 3D ab-initio Maxwell-Bloch computation. Nat. Phys. 2008, 4, 794–798. [Google Scholar] [CrossRef]
- Versteegh, M.A.M.; Vanmaekelbergh, D.; Dijkhuis, J.I. Room-Temperature Laser Emission of ZnO Nanowires Explained by Many-Body Theory. Phys. Rev. Lett. 2012, 108, 157402. [Google Scholar] [CrossRef]
- Versteegh, M.A.M.; van Capel, P.J.S.; Dijkhuis, J.I. Ultrafast all-optical gated amplifier based on ZnO nanowire lasing. Appl. Phys. Lett. 2012, 101, 021101. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Garcia, P.D.; Gregersen, S.; Ek, N.; Suhr, T.; Schubert, M.; Mork, J.; Stobbe, S.; Lodahl, P. Random nanolasing in the Anderson localized regime. Nat. Nanotechnol. 2014, 9, 285–289. [Google Scholar] [CrossRef] [Green Version]
- Frank, R.; Lubatsch, A.; Kroha, J. Theory of strong localization effects in disordered loss or gain media. Phys. Rev. B 2006, 73, 245107. [Google Scholar] [CrossRef]
- Frank, R.; Lubatsch, A.; Kroha, J. Light transport and localization in diffusive random lasers. J. Opt. A Pure Appl. Opt. 2011, 11, 114012. [Google Scholar] [CrossRef]
- Frank, R.; Lubatsch, A.; Kroha, J. Light transport and localization in diffusive random lasers. Ann. Der Phys. 2009, 18, 882–886. [Google Scholar] [CrossRef]
- Frank, R.; Lubatsch, A. Scalar wave propagation in random amplifying media: Influence of localization effects on length and time scales and threshold behavior. Phys. Rev. A 2011, 84, 013814. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Coherent transport and symmetry breaking—Laser dynamics of constrained granular matter. New J. Phys. 2014, 16, 083043. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Tuning the Quantum Efficiency of Random Lasers—Intrinsic Stokes-Shift and Gain. Sci. Rep. 2015, 5, 17000. [Google Scholar] [CrossRef]
- Gottardo, S.; Spienza, R.; Garcia, P.D.; Blanco, A; Wiersma, D.S.; Lopez, C. Resonance-driven random lasing. Nat. Photonics 2008, 2, 429–432. [Google Scholar] [CrossRef]
- Consoli, A.; Lopez, C. Decoupling gain and feedback in coherent random lasers: Experiments and simulations. Sci. Rep. 2015, 5, 16848. [Google Scholar] [CrossRef]
- Vollhardt, D.; Wölfle, P. Diagrammatic, self-consistent treatment of the Anderson localization problem in d <= 2 dimensions. Phys. Rev. B 1980, 22, 4666. [Google Scholar]
- Lubatsch, A.; Kroha, J.; Busch, K. Theory of light diffusion in disordered media with linear absorption or gain. Phys. Rev. B 2005, 71, 184201. [Google Scholar] [CrossRef] [Green Version]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Der Phys. 1908, 25, 377–445. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal Relations in Irreversible Processes. I + II. Phys. Rev. 1931, 37–28, 405–426, 2265. [Google Scholar] [CrossRef]
- Ward, J.C. An Identity in Quantum Electrodynamics. Phys. Rev. 1950, 78, 182. [Google Scholar] [CrossRef]
- Takahashi, Y. On the Generalized Ward Identity. Il Nuovo Cimento 1957, VI, 2231–2235. [Google Scholar] [CrossRef]
- Faist, J.; Capasso, F.; Sivco, D.L.; Sirtori, C.; Hutchinson, A.L.; Cho, A.Y. Quantum Cascade Laser. Science 1994, 264, 553–556. [Google Scholar] [CrossRef] [PubMed]
- Maret, G.; Sperling, T.; Buehrer, W.; Lubatsch, A.; Frank, R.; Aegerter, C.M. Reply to comment by F. Scheffold and D. Wiersma: Inelastic scattering puts in question recent claims of Anderson localization of light. Nat. Photonics 2013, 7, 934–935. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lubatsch, A.; Frank, R. A Self-Consistent Quantum Field Theory for Random Lasing. Appl. Sci. 2019, 9, 2477. https://doi.org/10.3390/app9122477
Lubatsch A, Frank R. A Self-Consistent Quantum Field Theory for Random Lasing. Applied Sciences. 2019; 9(12):2477. https://doi.org/10.3390/app9122477
Chicago/Turabian StyleLubatsch, Andreas, and Regine Frank. 2019. "A Self-Consistent Quantum Field Theory for Random Lasing" Applied Sciences 9, no. 12: 2477. https://doi.org/10.3390/app9122477
APA StyleLubatsch, A., & Frank, R. (2019). A Self-Consistent Quantum Field Theory for Random Lasing. Applied Sciences, 9(12), 2477. https://doi.org/10.3390/app9122477