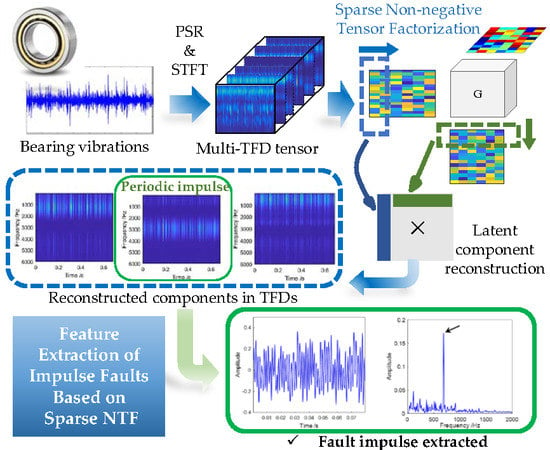
Feature Extraction of Impulse Faults for Vibration Signals Based on Sparse Non-Negative Tensor Factorization
Abstract
:Featured Application
Abstract
1. Introduction
2. Basic Theory of Non-Negative Tensor Factorization
2.1. Alternating Least Squares Algorithm for NTF
2.2. Hierarchical Alternating Least Squares Algorithm for NTF
2.3. HALS Algorithms for Sparse Non-Negative Tensor Factorization
3. Feature Extraction Method of an Impulse Fault
3.1. Principle of Phase Space Reconstruction
3.2. Time-Frequency Distribution Construction
3.3. Non-Negative Time-Frequency Tensor Analysis
3.4. Feature Extraction Method for Vibration Signals Based on Sparse Non-Negative Tensor Factorization
| Algorithm 1: Feature Extraction Method for Vibration Signals Based on SNTF |
| Step 1. The original one-dimensional signal is converted into a two-dimensional phase space by the PSR technique. |
| Step 2. Perform STFT on the phase point vectors to acquire multiple time-frequency distributions. |
| Step 3. Permutate the multiple TFDs to generate a third-order tensor . |
| Step 4. Select a reduced-dimensionality index , and employ the SNTF-HALS algorithm to decompose the above tensor . This step returns the frequency matrix , the time matrix , and the phase matrix . |
| Step 5. The reconstructed TFDs are obtained by , and the principal components (waveforms) are restored by ISTFT. |
| Step 6. Feature extraction. For a selected waveform, envelope demodulation is used to capture the characteristic frequency of certain damages. |
4. Experiments on Feature Extraction of Machinery Faults
4.1. Feature Extraction of Impulse Fault on Bearing Dataset—Case 1
4.1.1. Experimental Settings
4.1.2. Feature Extraction Based on SNTF
4.1.3. Comparisons with Other Methods
4.2. Feature Extraction of Impulse Fault on Bearing Dataset—Case 2
4.2.1. Experimental Settings
4.2.2. Feature Extraction Based on SNTF
4.2.3. Comparison and Analysis
4.3. Experiment on the Swashplate Axial Piston Pump
4.3.1. Experimental Settings
4.3.2. Feature Extraction Based on SNTF
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Randall, R.B.; Jérôme, A. Rolling Element Bearing Diagnostics—A Tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Chen, G.; Fenglin, L.; Wei, H. Sparse Discriminant Manifold Projections for Bearing Fault Diagnosis. J. Sound Vib. 2017, 399, 330–344. [Google Scholar] [CrossRef]
- Adamczak, S.; Krzysztof, S.; Mateusz, W. Comparative Study of Measurement Systems Used to Evaluate Vibrations of Rolling Bearings. Procedia Eng. 2017, 192, 971–975. [Google Scholar] [CrossRef]
- Tian, J.; Carlos, M.; Michael, H.A.; Michael, P. Motor Bearing Fault Detection Using Spectral Kurtosis-Based Feature Extraction Coupled with K-Nearest Neighbor Distance Analysis. IEEE Trans. Ind. Electron. 2016, 63, 1793–1803. [Google Scholar] [CrossRef]
- Jia, F.; Yaguo, L.; Hongkai, S.; Jing, L. Early Fault Diagnosis of Bearings Using an Improved Spectral Kurtosis by Maximum Correlated Kurtosis Deconvolution. Sensors 2015, 15, 29363–29377. [Google Scholar] [CrossRef] [PubMed]
- Zhivomirov, H. On the Development of STFT-analysis and ISTFT-synthesis Routines and their Practical Implementation. TEM J. 2019, 8, 56–64. [Google Scholar] [CrossRef]
- Rubini, R.; Meneghetti, U. Application of the Envelope and Wavelet Transform Analyses for the Diagnosis of Incipient Faults in Ball Bearings. Mech. Syst. Signal Process. 2001, 15, 287–302. [Google Scholar] [CrossRef]
- Lin, L.; Lei, S.; Fei, L.; Ben, N.; Guanghua, X. Sparse Envelope Spectra for Feature Extraction of Bearing Faults Based on Nmf. Appl. Sci. 2019, 9, 755. [Google Scholar]
- Leng, Y.; Zheng, A.; Fan, S. SVD component-envelope detection method and its application in the incipient fault diagnosis of rolling bearing. J. Vib. Eng. 2014, 5, 794–800. [Google Scholar] [CrossRef]
- Jiang, H.; Jin, C.; Guangming, D.; Tao, L.; Gang, C. Study on Hankel Matrix-Based SVD and Its Application in Rolling Element Bearing Fault Diagnosis. Mech. Syst. Signal Process. 2015, 52–53, 338–359. [Google Scholar] [CrossRef]
- Qingbo, H.; Xiaoxi, D. Time-Frequency Manifold for Machinery Fault Diagnosis. In Structural Health Monitoring; Springer: Cham, Switzerland, 2017; pp. 131–154. [Google Scholar] [CrossRef]
- Chaofan, H.; Yanxue, W. Multidimensional Denoising of Rotating Machine Based on Tensor Factorization. Mech. Syst. Signal Process. 2019, 122, 273–289. [Google Scholar]
- Makkiabadi, B.; Saeid, S. Factorization Based Blind Identification and Separation of Nonstationary Seizure Signals. In Proceedings of the 16th CSI International Symposium on Artificial Intelligence and Signal Processing (AISP 2012), Fars, Iran, 2–3 May 2012; pp. 617–622. [Google Scholar]
- Nielsen, S.F.V.; Morten, M. Non-Negative Tensor Factorization with Missing Data for the Modeling of Gene Expressions in the Human Brain. In Proceedings of the 2014 IEEE International Workshop on Machine Learning for Signal Processing (MLSP), Reims, France, 21–24 September 2014; pp. 1–6. [Google Scholar]
- Batmanghelich, N.; Aoyan, D.; Ben, T.; Christos, D. Regularized Tensor Factorization for Multi-Modality Medical Image Classification. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Toronto, ON, Canada, 18–22 September 2011; pp. 17–24. [Google Scholar]
- Wu, Q.; Liqing, Z.; Guangchuan, S. Robust Feature Extraction for Speaker Recognition Based on Constrained Nonnegative Tensor Factorization. J. Comput. Sci. Technol. 2010, 25, 783–792. [Google Scholar] [CrossRef]
- Rafailidis, D.; Alexandros, N. Modeling the Dynamics of User Preferences in Coupled Tensor Factorization. In Proceedings of the 8th ACM Conference on Recommender Systems, Silicon Valley, CA, USA, 6–10 October 2014; pp. 321–324. [Google Scholar]
- Zdunek, R.; Krzysztof, F.; Andrzej, W. Linked Cp Tensor Decomposition Algorithms for Shared and Individual Feature Extraction. Signal Process. Image Commun. 2019, 73, 37–52. [Google Scholar] [CrossRef]
- Cichocki, A.; Rafal, Z.; Anh, H.P.; Shun-ichi, A. Nonnegative Matrix and Tensor Factorizations; John Wiley & Sons: West Sussex, UK, 2009; p. 338. [Google Scholar]
- Sidiropoulos, N.D.; Lieven, D.L.; Xiao, F.; Kejun, H.; Evangelos, E.P.; Christos, F. Tensor Decomposition for Signal Processing and Machine Learning. IEEE Trans. Signal Process. 2017, 65, 3551–3582. [Google Scholar] [CrossRef]
- Yang, D.; Cancan, Y.; Zengbin, X.; Yi, Z.; Mao, G.; Changming, L. Improved Tensor-Based Singular Spectrum Analysis Based on Single Channel Blind Source Separation Algorithm and Its Application to Fault Diagnosis. Appl. Sci. 2017, 7, 418. [Google Scholar] [CrossRef]
- Li, G.; Lin, L.; Dan, L.; Maolin, L.; Bao, W.; Guanghua, X. The Source Separation of Multi-Channel Vibration Signal Based on Nonnegative Tensor Factorization. In Proceedings of the 10th International Conference on Communications, Circuits and Systems (ICCCAS), Chengdu, China, 22–24 December 2018; pp. 359–363. [Google Scholar]
- Wang, F.; Shouhai, C.; Jian, S.; Dawen, Y.; Lei, W.; Lihua, Z. Time-Frequency Fault Feature Extraction for Rolling Bearing Based on the Tensor Manifold Method. Math. Probl. Eng. 2014, 2014, 2014. [Google Scholar] [CrossRef]
- Cichocki, A.; Rafal, Z.; Shun-ichi, A. Hierarchical ALS Algorithms for Nonnegative Matrix and 3d Tensor Factorization. In Proceedings of the International Conference on Latent Variable Analysis and Signal Separation, London, UK, 9–12 September 2007; pp. 169–176. [Google Scholar]
- Cichocki, A.; Phan, A.H.; Zdunek, R.; Zhang, L.Q. Flexible Component Analysis for Sparse, Smooth, Nonnegative Coding or Representation. In Proceedings of the International Conference on Neural Information Processing, Kitakyushu, Japan, 13–16 November 2008; pp. 811–820. [Google Scholar]
- Cichocki, A.; Anh, H.P.; Cesar, C. Flexible HALS Algorithms for Sparse Non-Negative Matrix/Tensor Factorization. In Proceedings of the 2008 IEEE Workshop on Machine Learning for Signal Processing, Cancun, Mexico, 16–19 Octorber 2008; pp. 73–78. [Google Scholar]
- Stanković, L. A Measure of Some Time–Frequency Distributions Concentration. Signal Process. 2001, 81, 621–631. [Google Scholar] [CrossRef]
- Qiu, H.; Jay, L.; Jing, L.; Gang, Y. Wavelet Filter-Based Weak Signature Detection Method and Its Application on Rolling Element Bearing Prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Smith, W.A.; Robert, B.R. Rolling Element Bearing Diagnostics Using the Case Western Reserve University Data: A Benchmark Study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]
- Cai, S.; Jianfeng, Q.; Zeping, W.; Chunyan, L. Feature Extraction of Rolling Bearing Incipient Fault Using an Improved SCA-Based UBSS Method. In Proceedings of the International Conference on Mechatronics and Intelligent Robotics, Kunming, China, 19–20 May 2019; pp. 994–1002. [Google Scholar]


























| Bearing Model | Running Speed | Sampling Rate | Fault Position | Characteristic Frequency |
|---|---|---|---|---|
| Rexnord ZA-2115 | 2000 RPM | 20,000 Hz | Outer Ring | 236.9 Hz |
| Bearing Model | Running Speed | Sampling Rate | Fault Position | Characteristic Frequency |
|---|---|---|---|---|
| SKF 6203-2RS | 1730 RPM | 12,000 Hz | Inner Ring | 143.2 Hz |
| Bearing Model | Running Speed | Sampling Rate | Fault Characteristic Frequency |
|---|---|---|---|
| D8111Q | 3415 RPM | 25,600 Hz | 689.9 Hz |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, L.; Wen, H.; Liu, F.; Li, G.; Li, M. Feature Extraction of Impulse Faults for Vibration Signals Based on Sparse Non-Negative Tensor Factorization. Appl. Sci. 2019, 9, 3642. https://doi.org/10.3390/app9183642
Liang L, Wen H, Liu F, Li G, Li M. Feature Extraction of Impulse Faults for Vibration Signals Based on Sparse Non-Negative Tensor Factorization. Applied Sciences. 2019; 9(18):3642. https://doi.org/10.3390/app9183642
Chicago/Turabian StyleLiang, Lin, Haobin Wen, Fei Liu, Guang Li, and Maolin Li. 2019. "Feature Extraction of Impulse Faults for Vibration Signals Based on Sparse Non-Negative Tensor Factorization" Applied Sciences 9, no. 18: 3642. https://doi.org/10.3390/app9183642
APA StyleLiang, L., Wen, H., Liu, F., Li, G., & Li, M. (2019). Feature Extraction of Impulse Faults for Vibration Signals Based on Sparse Non-Negative Tensor Factorization. Applied Sciences, 9(18), 3642. https://doi.org/10.3390/app9183642