Reversible Data Hiding in Encrypted Color Halftone Images with High Capacity

Abstract

In recent years, reversible data hiding (RDH) has become a research hotspot in the field of multimedia security that has aroused more and more researchers’ attention. Most of the existing RDH algorithms are aiming at continuous-tone images. For RDH in encrypted halftone images (RDH-EH), the original cover image cannot be recovered losslessly after the watermark is extracted. For some application scenarios such as medical or military images sharing, reversibility is critical. In this paper, a reversible data hiding scheme in encrypted color halftone images (RDH-ECH) is proposed. In the watermark embedding procedure, the cover image is copied into two identical images to increase redundancy. We use wet paper code to embed the watermark into the image blocks. Thus, the receiver only needs to process the image blocks by the check matrices in order to extract the watermarks. To increase embedding capacity, we embed three layers in the embedding procedure and combine the resulting images into one image for convenience of transmission. From the experimental results, it can be concluded that the original image can be restored entirely after the watermarks are extracted. Besides, for marked color halftone images, our algorithm can implement high embedding capacity and moderate visual quality.

1. Introduction

Data hiding refers to making the cover image imperceptibly and keeping the existence of the hidden data confidential. We call the hidden data a watermark. Reversible data hiding (RDH) is a technique that the cover image can be restored losslessly after the watermark is extracted [1]. This characteristic makes RDH suitable for high authentication scenarios, such as medical image processing or military communication. It is widely used in applications such as law forensics [2,3,4], military imagery, medical imagery [5], cloud storage [6,7], copyright protection [8,9,10,11], etc. The traditional RDH schemes can be classified into several categories such as lossless compression [12], difference expansion (DE) [13,14], histogram shifting (HS) [15,16], and pixel prediction [17]. Combined with image encryption schemes, many algorithms of RDH in encrypted domain (RDH-ED) have been proposed. According to whether the image decryption and data extraction procedures are separated, the RDH-ED algorithms can be categorized into two types: (1) inseparable algorithms; and (2) separable algorithms.

For inseparable algorithms, Puech et al. [18] applied RDH algorithms to encrypted images by embedding additional bits into pixels blocks encrypted by AES (Advanced Encryption Standard). In 2011, Zhang proposed an algorithm that flips the three least significant bits (LSBs) of half of the pixels in each block [19]. The embedded additional data can be extracted after the encrypted image with additional data being decrypted. Hong et al. [20] improved Zhang’s algorithm [19] by adopting a better measurement method for the smoothness of blocks and using the side-match scheme to decrease the error rate of extraction.

For separable algorithms, Zhang proposed a separable RDH-ED, in which image decryption and data extraction procedures are independent operations [21]. Qian et al. introduced an algorithm that solved a problem of Zhang’s scheme [22], which cannot recover the original image completely. In [23], Ma et al. proposed an improved embedding capacity algorithm that needed to reserve room before encryption. Besides, the embedding capacity of the encrypted image is improved. Fu et al. [24] proposed an effective algorithm with adaptive encoding strategy. MSB (most significant bit) layers of embeddable blocks are adaptively compressed according to occurrence frequency of MSB in order to vacate room for data accommodation.

As for halftone images, there are few RDH algorithms available in the literature. Since the redundancy left in halftone image is low, most RDH algorithms for continuous-tone images cannot be directly used in halftone images. Depending on whether the continuous-tone image is available to the embedding process, the RDH algorithms for halftone images can be classified into two categories:

(1)

Only the halftone image joins the embedding process. Fu and Oscar proposed RDH-EH algorithm by forced complementary toggling at pseudo-random locations if only the halftone image is available [25]. Lien et al. introduced a high-capacity RDH method for ordered dithered halftone images, which applied dither matrix to pixel pairs so that abundant data can be hidden into these pixel pairs [26]. Kim et al. proposed a separable RDH algorithm, which used Hamming codes to embed watermark [27].

(2)

The continuous-tone image joins the embedding process. For the situation in which the original continuous-tone image is available, Fu and Oscar proposed an algorithm that integrates the data hiding operation into the error diffusion process [25]. Lo et al.’s algorithm embedded the binary data into the halftone images with reference to the original continuous-tone image by evaluating the absolute difference between the neighboring gray-level pixels [28]. This method is extended from that of Fu and Au [25].

For the problem of RDH in encrypted halftone image, the remaining redundancy is very difficult to utilize. Designing RDH algorithm for encrypted halftone image is a challenging problem. In this paper, we focus on the topic of RDH in encrypted color halftone images (RDH-ECH), where the original cover image can be restored from the stego image after extracting the watermark. To overcome the problem that in the encrypted halftone images little redundancy exists, we adopt dual cover images in the embedding process. The role of dual images are different from the two shares in visual cryptography [29,30]. Dual images are used to create redundancy for data hiding. We also combine the resulting stego images for facilitating transmission. Because of the reversibility, the proposed method can be applied to data hiding applications such as the healthcare industry and online distribution systems. Unless owning the secret keys, attackers cannot restore the original halftone image and watermark losslessly.

The remaining part of this paper is organized as follows. Section 2 introduces the necessary background of the proposed algorithm which is wet paper code scheme. The proposed scheme is elaborated in Section 3. The experimental results are presented in Section 4, which includes test of lossless recovery, security, visual quality, embedding capacity, and computational complexity. Finally, Section 5 concludes this paper.

Unless otherwise stated, all vectors are column vectors by default.

2. Related Works

In this section, we briefly describe wet paper code (WPC) for RDH. WPC is similar to matrix embedding as both are based on syndrome codes. Let us assume that the sender has a cover binary vector $\mathit{x}={\left\{x_i\right\}}_{i=1}^n$ and a set of indices $Q\subset \{1,\cdots ,n\}$ ($\left|Q\right|=k$). The k bits are called dry elements that can be modified to embed watermark, and the remaining $(n-k)$ bits are called wet elements, which remain the same during embedding procedure.

To embed m bits $\mathit{m}\in {\left\{0,1\right\}}^m$, the sender modifies the changeable bits so that the stego binary vector $\mathit{y}$ satisfies

$$\mathit{D}\times \mathit{y}=\mathit{m}$$

(1)

where $\mathit{D}$ is an $m\times n$ parity check matrix produced by the pseudo-random number generator. The receiver can extracts the watermark from $\mathit{y}$ by calculating the syndrome $\mathit{Dy}$.

To solve the system of linear equations of Equation (1), we rewrite it as

$$\mathit{D}\times \mathit{v}=\mathit{m}-\mathit{D}\times \mathit{x}$$

(2)

where $\mathit{v}=\mathit{y}-\mathit{x}$. There are k unknowns ${\mathit{v}}_j$ which are nonzeros, whereas the remaining $(n-k)$ values ${\mathit{v}}_i$ are zeros. Thus, on the left-hand side, we remove from $\mathit{D}$ all $(n-k)$ columns i and also remove from $\mathit{v}$ all $(n-k)$ elements ${\mathit{v}}_i$. Keeping the same symbol for $\mathit{v}$, Equation (2) now becomes

$$\mathit{H}\times \mathit{v}=\mathit{m}-\mathit{D}\times \mathit{x}$$

(3)

where $\mathit{H}$ is a binary $m\times k$ matrix consisting of those columns of $\mathit{D}$, and $\mathit{v}$ is an unknown binary $k\times 1$ vector holding the embedding changes. According to the solvability of linear equations, the value of $\mathit{v}$ is solved. Thus, we get the modified binary column vector $\mathit{y}$ based on $\mathit{y}=\mathit{v}+\mathit{x}$.

3. Proposed Scheme

In this section, we elaborate on our RDH scheme for encrypted color halftone image. The block diagram of our method is illustrated in Figure 1.

The overall procedure of proposed RDH-EH algorithm can be briefly described as follows. First, the image owner encrypts the original halftone image $\mathit{O}$ using encryption key $K_e$ and then sends the produced cover image $\mathit{I}$ to the service provider. The provider first converts $\mathit{I}$ into channel images $\mathit{R}$, $\mathit{G}$, and $\mathit{B}$. For cover image $\mathit{R}$, he copies it into two identical cover image ${\mathit{R}}^{\prime }$ and ${\mathit{R}}^{″}$. After the first WPC embedding procedure is complete, two stego image ${\mathit{F}}_{R^{\prime }}$ and ${\mathit{F}}_{R^{″}}$ are generated. The stego image ${\mathit{F}}_{R^{\prime }}$ is the cover image of the second WPC embedding process and is copied into two identical images ${\mathit{F}}_{R^{\prime }}^{\prime }$ and ${\mathit{F}}_{R^{\prime }}^{″}$. There will be stego images ${\mathit{S}}_{R^{\prime }}$ and ${\mathit{S}}_{R^{″}}$ after the second WPC. Next, the service provider uses ${\mathit{S}}_{R^{\prime }}$ in the third embedding procedure and also copies it into two images ${\mathit{S}}_{R^{\prime }}^{\prime }$ and ${\mathit{S}}_{R^{\prime }}^{″}$. After that, two stego images ${\mathit{T}}_{R^{\prime }}$ and ${\mathit{T}}_{R^{″}}$ are produced. Then, the provider combines ${\mathit{T}}_{R^{\prime }}$, ${\mathit{F}}_{R^{″}}$, ${\mathit{S}}_{R^{″}}$, and ${\mathit{T}}_{R^{″}}$ into one image ${\mathit{C}}_R$; the specific way of combining them is elaborated in Section 3.2. For cover images $\mathit{G}$ and $\mathit{B}$, be executing the same embedding process as described above, the stego images ${\mathit{C}}_G$ and ${\mathit{C}}_B$ are generated. Finally, the service provider merges stego images ${\mathit{C}}_R$, ${\mathit{C}}_G$, and ${\mathit{C}}_B$ into one stego image $\mathit{C}$.

On the receiver’s side, depending on the limits of authority, he can do different operations to the image. If the receiver has only the data-hiding key $K_d$, he can extract the watermark $\mathit{b}$. If he has both $K_e$ and $K_d$, the receiver can extract the watermark $\mathit{b}$ and recover the original image $\mathit{O}$. Because we combine four images into one stego image during the embedding procedure, if the receiver has only the $K_e$, he does not have access to the content of the original image after decryption.

3.1. Image Encryption

Suppose that the size of the original color halftone image $\mathit{O}$ is $N_1\times N_2\times 3$. As each pixel in a halftone image is represented by one bit, the total number of bits N is $N_1\times N_2\times 3$. Let the pixel value at position $(u,v,t)$ be $a_{u,v,t}$, where $\{1\le$ u $\le N_1\}$, $\{1\le$ v $\le N_2\}$, and $\{1\le$ t $\le 3\}$. To encrypt $\mathit{O}$, we calculate exclusive-or operations between $a_{u,v,t}$ and the pseudo-random bits $k_{u,v,t}$ as

$$e_{u,v,t}=a_{u,v,t}\oplus k_{u,v,t}$$

(4)

where $e_{u,v,t}$ is the pixel value of cover image $\mathit{I}$, $k_{u,v,t}$ is generated by a stream cipher scheme with encryption key $K_e$. For example, one may use any secure stream ciphers such as RC4 [31].

3.2. Data Embedding

In this subsection, we describe the watermark embedding procedure which adopts dual images. The diagram of data embedding procedure is illustrated in Figure 2. Given the cover image $\mathit{I}$, the service provider first splits the cover image into $\mathit{R}$, $\mathit{G}$, and $\mathit{B}$ channels and does the same operation to each channel as follows.

(1)

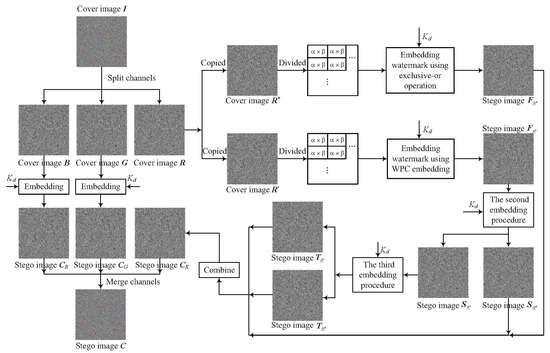
Taking cover image $\mathit{R}$ as an example, for the first WPC embedding, the service provider first copies it into two identical cover images ${\mathit{R}}^{\prime }$ and ${\mathit{R}}^{″}$. We partition each of them into non-overlapping blocks of size $\alpha \times \beta$; each block is denoted as ${\mathit{L}}_{\ell j},j=1,\cdots ,w$ and $\ell =1,2$, where w is the total number of blocks for each channel image:

$$w=⌊\frac{N_1}{\alpha }⌋\times ⌊\frac{N_2}{\beta }⌋$$

(5)

where $\lfloor x\rfloor$ rounds x to the nearest integer towards $-\infty$.

The service provider first encrypts the watermark $b_{\gamma i}$ by

$${\theta }_{\gamma i}=b_{\gamma i}\oplus p_{\gamma i}$$

(6)

where $\gamma$$=1,\cdots ,9$, because we perform the embedding process three times on one channel image and there are three channels, ${\theta }_{\gamma i}$ is the encrypted watermark, and $p_{\ell i}$ is determined via standard stream cipher using data-hiding key $K_d$. Then, for every four bits of each ${\theta }_{\gamma i}$, we group them to a block. Thus, the jth watermark block ${\mathit{\theta }}_{\gamma i}$ is obtained as

$${\mathit{\theta }}_{\gamma j}={\left[{\theta }_{\gamma (4j-3)}{\theta }_{\gamma (4j-2)}{\theta }_{\gamma (4j-1)}{\theta }_{\gamma \left(4j\right)}\right]}^T,1\le j\le w$$

(7)

For cover image ${\mathit{R}}^{\prime }$, we read one block ${\mathit{L}}_{1j}$, and convert it into a column vector ${\mathit{x}}_{1j}$. Let the first four elements of ${\mathit{x}}_{1j}$ be the dry elements of WPC. Generate the pseudo-random binary matrix ${\mathit{D}}_{1j}$ of dimensions $q\times n$ by using $K_d$. Then, to generate the column vector ${\mathit{y}}_{1j}$, which satisfies

$${\mathit{D}}_{1j}\times {\mathit{y}}_{1j}={\mathit{\theta }}_{1j}$$

(8)

we need first calculate ${\mathit{s}}_{1j}={\mathit{D}}_{1j}\times {\mathit{x}}_{1j}$ according to Equation (3). Next, the exclusive-or operations between ${\mathit{s}}_{1j}$ and ${\mathit{\theta }}_{1j}$ are implemented. After that, the last four columns of each ${\mathit{D}}_{1j}$ are removed to form ${\mathit{H}}_{1j}$. Finally, ${\mathit{v}}_{1j}$ is solved based on the solvability of the linear equations and then

$${\mathit{y}}_{1j}={\mathit{v}}_{1j}+{\mathit{x}}_{1j}$$

(9)

Having ${\mathit{y}}_{1j}$, new blocks ${\mathit{L}}_{1j}^{\prime }$ are formed and, then, these blocks are combined to produce stego image ${\mathit{F}}_{R^{\prime }}$ by following raster scanning order.

As for cover image ${\mathit{R}}^{″}$, we embed each watermark vector ${\mathit{\theta }}_{1j}$ into ${\mathit{L}}_{2j}$. First, the first four bits of each block ${\mathit{L}}_{2j}$ are converted to a vector ${\mathit{z}}_{1j}$. Then, embed watermark vector into ${\mathit{z}}_{1j}$ by

$${\overline{\mathit{z}}}_{1j}={\mathit{z}}_{1j}\oplus {\mathit{\theta }}_{1j}$$

(10)

After all blocks of ${\mathit{R}}^{″}$ are modified, we obtain new blocks ${\mathit{L}}_{2j}^{\prime }$ and also stego image ${\mathit{F}}_{R^{″}}$.

(2)

For the second WPC embedding, we take image ${\mathit{F}}_{R^{\prime }}$ as the cover image. The same as the above procedure, the service provider first copies ${\mathit{F}}_{R^{\prime }}$ into two identical images ${\mathit{F}}_{R^{\prime }}^{\prime }$ and ${\mathit{F}}_{R^{\prime }}^{″}$. For cover image ${\mathit{F}}_{R^{\prime }}^{\prime }$, we take the same WPC embedding operation as in Step (1) and then generate stego image ${\mathit{S}}_{R^{\prime }}$. For cover image ${\mathit{F}}_{R^{\prime }}^{″}$, we embed watermark vector in it and then we get stego image ${\mathit{S}}_{R^{″}}$.

(3)

As for the third WPC embedding, we take image ${\mathit{S}}_{R^{\prime }}$ as the cover image and copy it into two same images ${\mathit{S}}_{R^{\prime }}^{\prime }$ and ${\mathit{S}}_{R^{\prime }}^{″}$. After the third embedding procedure, stego images ${\mathit{T}}_{R^{\prime }}$ and ${\mathit{T}}_{R^{″}}$ are produced.

(4)

Finally, we combine four images ${\mathit{T}}_{R^{\prime }}$, ${\mathit{F}}_{R^{″}}$, ${\mathit{S}}_{R^{″}}$, and ${\mathit{T}}_{R^{″}}$ into one image ${\mathit{C}}_R$ using $K_d$. As demonstrated in Figure 3, supposing that each image is $2\times 2$ sized and the pixels are represented by different color, we stagger-stitch these pixels up–down and left–right.

The reason why we adopt triple embedding is that it produces four stego images after embedding. Thus, the aspect ratio of the combined image is the same as the original image $\mathit{O}$. The different aspect ratio of the combined image for different levels of embedding is listed in

Table 1. Aspect ratios resulting from different embedding levels.

Embedding Levels	Number of Result Images	Aspect Ratio
Zero	1	$N_1$:$N_2$
Once	2	$2N_1$:$N_2$
Twice	3	$3N_1$:$N_2$
Triple	4	$N_1$:$N_2$

. The comparison result shows that triple embedding is suitable for image combination as it keeps the aspect ratio of the original image.

For cover image $\mathit{G}$ and $\mathit{B}$, we perform the same embedding procedure to them, and then we have combined stego images ${\mathit{C}}_G$ and ${\mathit{C}}_B$. Finally, we merge the three channel images ${\mathit{C}}_R$, ${\mathit{C}}_G$, and ${\mathit{C}}_B$ and then the stego image $\mathit{C}$ is generated. The proposed data embedding procedure is summarized in Algorithm 1.

Algorithm 1 Data embedding.

Input: Cover image $\mathit{I}$, watermark $\mathit{b}$, and data-hiding key $K_d$ Output: Stego image $\mathit{C}$ 1: Split cover image $\mathit{I}$ into channel images $\mathit{R}$, $\mathit{G}$, and $\mathit{B}$ 2: functionTripleEmbedding($\mathit{I},\mathit{b},K_d$) 3:   Encrypt watermark ${\mathit{b}}_i$ to ${\theta }_i$ using Equation (6) 4:   Group ${\theta }_i$ to block ${\mathit{\theta }}_j$ 5:   Copy $\mathit{I}$ into ${\mathit{I}}^{\prime }$ and ${\mathit{I}}^{″}$ 6:   For ${\mathit{I}}^{\prime }$ do: 7:   Divide ${\mathit{I}}^{\prime }$ into blocks ${\mathit{L}}_{1j}$ 8:    9:   for $j=1$ to w do 10:     ${\mathit{x}}_j\leftarrow {\mathit{L}}_{1j}$ 11:     Generate ${\mathit{D}}_j$ using $K_d$ 12:     ${\mathit{s}}_j={\mathit{D}}_j\times {\mathit{x}}_j$ 13:     ${\overline{\mathit{s}}}_j={\mathit{s}}_j\oplus {\mathit{\theta }}_j$ 14:     ${\mathit{H}}_j\leftarrow {\mathit{D}}_j$ 15:     ${\mathit{v}}_j\leftarrow ({\mathit{H}}_j{\mathit{v}}_j={\overline{\mathit{s}}}_j$) 16:     ${\mathit{y}}_j={\mathit{v}}_j+{\mathit{x}}_j$ 17:     Blocks ${\mathit{L}}_{1j}^{\prime }$←${\mathit{y}}_j$ 18:   end for 19:   Stego image ${\mathit{F}}_{I^{\prime }}$←${\mathit{L}}_{1j}^{\prime }$ 20:   For ${\mathit{I}}^{″}$ do: 21:   Divided ${\mathit{I}}^{″}$ into blocks ${\mathit{L}}_{2j}$ 22:    23:   for $j=1$ to w do 24:     Assign ${\mathit{z}}_j$ with the first four bits of ${\mathit{L}}_{2j}$ 25:     ${\overline{\mathit{z}}}_j={\mathit{z}}_j\oplus {\mathit{\theta }}_j$ 26:     Assign ${\overline{\mathit{z}}}_j$ to the first four bits of ${\mathit{L}}_{2j}^{\prime }$ 27:   end for 28:   Stego image ${\mathit{F}}_{I^{″}}$←${\mathit{L}}_{2j}^{\prime }$     //The first embedding process ends 29:   For ${\mathit{F}}_{I^{\prime }}$ do: 30:   Repeat Steps 5–19, generate stego image ${\mathit{S}}_{I^{\prime }}$ 31:   Repeat Steps 20–28, generate stego image ${\mathit{S}}_{I^{″}}$ 32:   //The second embedding process ends 33:   For ${\mathit{S}}_{I^{\prime }}$ do: 34:   Repeat Steps 5–19, generate stego image ${\mathit{T}}_{I^{\prime }}$ 35:   Repeat Steps 20–28, generate stego image ${\mathit{T}}_{I^{″}}$ 36:   //The third embedding process ends 37:   ${\mathit{C}}_I$ combined from ${\mathit{T}}_{I^{\prime }}$, ${\mathit{F}}_{I^{″}}$, ${\mathit{S}}_{I^{″}}$, and ${\mathit{T}}_{I^{″}}$ 38: end function 39: ${\mathit{C}}_R=\mathrm{T}\mathrm{R}\mathrm{I}\mathrm{P}\mathrm{L}\mathrm{E}\mathrm{E}\mathrm{M}\mathrm{B}\mathrm{E}\mathrm{D}\mathrm{D}\mathrm{I}\mathrm{N}\mathrm{G}(\mathit{R},\mathit{b},K_d)$ 40: ${\mathit{C}}_G=\mathrm{T}\mathrm{R}\mathrm{I}\mathrm{P}\mathrm{L}\mathrm{E}\mathrm{E}\mathrm{M}\mathrm{B}\mathrm{E}\mathrm{D}\mathrm{D}\mathrm{I}\mathrm{N}\mathrm{G}(\mathit{G},\mathit{b},K_d)$ 41: ${\mathit{C}}_B=\mathrm{T}\mathrm{R}\mathrm{I}\mathrm{P}\mathrm{L}\mathrm{E}\mathrm{E}\mathrm{M}\mathrm{B}\mathrm{E}\mathrm{D}\mathrm{D}\mathrm{I}\mathrm{N}\mathrm{G}(\mathit{B},\mathit{b},K_d)$ 42: Merge channel images ${\mathit{C}}_R$, ${\mathit{C}}_G$ and ${\mathit{C}}_B$ to color image $\mathit{C}$ 43: return Stego image $\mathit{C}$

3.3. Extraction and Recovery

In this section, we discuss the two situations on the receiver’s side. Depending on the different types of key, the receiver can extract the watermark (having $K_d$) or recover the image after extraction (having both $K_e$ and $K_d$). Because we combine the images into one stego image, if we only decrypt stego image $\mathit{C}$, the content of the original image cannot be directly presented. The proposed procedure of extraction and recovery is summarized in Algorithm 2.

Algorithm 2 Extraction and recovery.

Input: Stego image $\mathit{C}$, secret key $K_e$ and $K_d$ Output: Original halftone image $\mathit{O}$ and watermark $b_{\ell i}$ 1: Split stego image $\mathit{O}$ into channel images ${\mathit{C}}_R$, ${\mathit{C}}_G$, and ${\mathit{C}}_B$ 2: functionDataExtraction($\mathit{C},K_d$) 3:   Separate $\mathit{C}$ to four images ${\mathit{T}}_{C^{\prime }}$, ${\mathit{F}}_{C^{″}}$, ${\mathit{S}}_{C^{″}}$, and ${\mathit{T}}_{C^{″}}$ 4:   Divide ${\mathit{T}}_{C^{\prime }}$ into blocks ${\mathit{W}}_{1j}$ 5:   Divide ${\mathit{T}}_{C^{″}}$ into blocks ${\mathit{W}}_{2j}$ 6:    7:   for $j=1$ to w do 8:     ${\mathit{y}}_{3j}^{\prime }\leftarrow {\mathit{W}}_{1j}$ 9:     Generated ${\mathit{D}}_{3j}$ using $K_d$ 10:     ${\mathit{\theta }}_{3j}={\mathit{D}}_{3j}\times {\mathit{y}}_{3j}^{\prime }$ 11:     Assign ${\overline{\mathit{z}}}_{3j}$ to the first four bits of ${\mathit{W}}_{2j}$ 12:     ${\mathit{z}}_{3j}^{\prime }={\overline{\mathit{z}}}_{3j}\oplus {\mathit{\theta }}_{3j}$ 13:   end for 14:   Stego image ${\mathit{S}}_{C^{\prime }}$←${\mathit{z}}_{3j}^{\prime }$ 15:   Divide ${\mathit{S}}_{C^{\prime }}$ into blocks ${\mathit{E}}_{1j}$ 16:   Divide ${\mathit{S}}_{C^{″}}$ into blocks ${\mathit{E}}_{2j}$ 17:    18:   for $j=1$ to w do 19:     ${\mathit{y}}_{2j}^{\prime }\leftarrow {\mathit{E}}_{1j}$ 20:     Generated ${\mathit{D}}_{2j}$ using $K_d$ 21:     ${\mathit{\theta }}_{2j}={\mathit{D}}_{2j}\times {\mathit{y}}_{2j}^{\prime }$ 22:     Assign ${\overline{\mathit{z}}}_{2j}$ to the first four bits of ${\mathit{E}}_{2j}$ 23:     ${\mathit{z}}_{2j}^{\prime }={\overline{\mathit{z}}}_{2j}\oplus {\mathit{\theta }}_{2j}$ 24:   end for 25:   Stego image ${\mathit{F}}_{C^{\prime }}$←${\mathit{z}}_{2j}^{\prime }$ 26:   Divide ${\mathit{F}}_{C^{\prime }}$ into blocks ${\mathit{P}}_{1j}$ 27:   Divide ${\mathit{F}}_{C^{″}}$ into blocks ${\mathit{P}}_{2j}$ 28:    29:   for $j=1$ to w do 30:     ${\mathit{y}}_{1j}^{\prime }\leftarrow {\mathit{P}}_{1j}$ 31:     Generated ${\mathit{D}}_{1j}$ using $K_d$ 32:     ${\mathit{\theta }}_{1j}={\mathit{D}}_{1j}\times {\mathit{y}}_{1j}^{\prime }$ 33:     Assign ${\overline{\mathit{z}}}_{1j}$ to the first four bits of ${\mathit{P}}_{2j}$ 34:     ${\mathit{z}}_{1j}^{\prime }={\overline{\mathit{z}}}_{1j}\oplus {\mathit{\theta }}_{1j}$ 35:   end for 36:   Cover image ←${\mathit{z}}_{1j}^{\prime }$ 37: end function 38: $(\mathit{R},{\mathit{\theta }}_{1j},{\mathit{\theta }}_{2j}{\mathit{\theta }}_{3j})=\mathrm{D}\mathrm{A}\mathrm{T}\mathrm{A}\mathrm{E}\mathrm{x}\mathrm{T}\mathrm{R}\mathrm{A}\mathrm{C}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}({\mathit{C}}_R,K_d)$ 39: $(\mathit{G},{\mathit{\theta }}_{4j},{\mathit{\theta }}_{5j},{\mathit{\theta }}_{6j})=\mathrm{D}\mathrm{A}\mathrm{T}\mathrm{A}\mathrm{E}\mathrm{x}\mathrm{T}\mathrm{R}\mathrm{A}\mathrm{C}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}({\mathit{C}}_G,K_d)$ 40: $(\mathit{B},{\mathit{\theta }}_{7j},{\mathit{\theta }}_{8j},{\mathit{\theta }}_{9j})=\mathrm{D}\mathrm{A}\mathrm{T}\mathrm{A}\mathrm{E}\mathrm{x}\mathrm{T}\mathrm{R}\mathrm{A}\mathrm{C}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}({\mathit{C}}_B,K_d)$ 41: $b_{\ell i}={\theta }_{\ell i}\oplus p_{\ell i}^{\prime }$ 42: Merge images $\mathit{R}$, $\mathit{G}$ and $\mathit{B}$ to cover image $\mathit{I}$ 43: Decrypt $\mathit{I}$ using Equation(16) 44: return Watermark $b_{\ell i}$ and original image $\mathit{O}$

3.3.1. Watermark Extraction

When the receiver has only the data-hiding key $K_d$, he can extract the watermark from stego image $\mathit{C}$. The receiver first divides the image into channel images ${\mathit{C}}_R$, ${\mathit{C}}_G$, and ${\mathit{C}}_B$. For stego image ${\mathit{C}}_R$, he separates it into four images ${\mathit{T}}_{R^{\prime }}$, ${\mathit{F}}_{R^{″}}$, ${\mathit{S}}_{R^{″}}$, and ${\mathit{T}}_{R^{″}}$. Stego images ${\mathit{T}}_{R^{\prime }}$ and ${\mathit{T}}_{R^{″}}$ are divided into $\alpha \times \beta$ non-overlapping blocks, each of which is denoted as ${\mathit{W}}_{\ell j},j=1,\cdots ,w$ and $\ell =1,2$. Convert each of ${\mathit{W}}_{1j}$ to a column vector ${\mathit{y}}_{3j}^{\prime }$, and, the following equation is calculated to obtain the encrypted watermark blocks ${\mathit{\theta }}_{3j}$ according to Equation (8)

$${\mathit{\theta }}_{3j}={\mathit{D}}_{3j}\times {\mathit{y}}_{3j}^{\prime }$$

(11)

where ${\mathit{D}}_{3j}$ is pseudo-random binary matrix generated by $K_d$. Then, read the first four bits of ${\mathit{W}}_{2j}$ and convert them to a column vector ${\overline{\mathit{z}}}_{3j}$. Next, replace the first four bits of every block by

$$\begin{array}{cc}\hfill {\mathit{z}}_{3j}^{\prime }& ={\overline{\mathit{z}}}_{3j}\oplus {\mathit{\theta }}_{3j}\hfill \\ \hfill & ={\mathit{z}}_{3j}\oplus {\mathit{\theta }}_{3j}\oplus {\mathit{\theta }}_{3j}\hfill \\ \hfill & ={\mathit{z}}_{3j}\hfill \end{array}$$

(12)

After that, stego image ${\mathit{S}}_{R^{\prime }}$ is acquired. We divide ${\mathit{S}}_{R^{\prime }}$ and ${\mathit{S}}_{R^{″}}$ into $1\times 8$ non-overlapping blocks, each of which is denoted as ${\mathit{E}}_{\ell j},j=1,\cdots ,w$ and $\ell =1,2$. Convert each of ${\mathit{E}}_{1j}$ into vectors ${\mathit{y}}_{2j}^{\prime }$, and then into the encrypted watermark blocks ${\mathit{\theta }}_{2j}$ by calculating

$${\mathit{\theta }}_{2j}={\mathit{D}}_{2j}\times {\mathit{y}}_{2j}^{\prime }$$

(13)

Next, the first four bits of each block of ${\mathit{E}}_{1j}$ are converted to column vectors ${\overline{\mathit{z}}}_{2j}$. Then, replace them by

$${\mathit{z}}_{2j}^{\prime }={\overline{\mathit{z}}}_{2j}\oplus {\mathit{\theta }}_{2j}$$

(14)

Thus, stego image ${\mathit{F}}_{R^{\prime }}$ is achieved, and we also get cover image $\mathit{R}$ and encrypted watermark blocks ${\mathit{\theta }}_{1j}$ by performing the same process using ${\mathit{F}}_{R^{\prime }}$ and ${\mathit{F}}_{R^{″}}$. In addition, cover images $\mathit{G}$ and $\mathit{B}$ as well as watermark blocks ${\mathit{\theta }}_{{\gamma }^{\prime }j}$ (${\gamma }^{\prime }$$=4,\cdots ,9$) are also generated from stego images ${\mathit{C}}_G$ and ${\mathit{C}}_B$. We concatenate ${\mathit{\theta }}_{\gamma j}$ to column vectors ${\mathit{\theta }}_{\gamma i}$ and get watermark $b_{\gamma i}$ by calculating

$$b_{\gamma i}={\theta }_{\gamma i}\oplus p_{\gamma i}^{\prime }$$

(15)

where $\gamma$$=1,\cdots ,9$, $p_{\gamma i}^{\prime }$ is determined via standard stream cipher using data-hiding key $K_d$. Finally, images $\mathit{R}$, $\mathit{G}$ and $\mathit{B}$ are merged to compose cover image $\mathit{I}$.

3.3.2. Image Recovery

If the receiver has both $K_e$ and $K_d$, he can recover the original halftone image after watermark extraction. By decrypting the cover image $\mathit{I}$ we get in Section 3.3.1, the original image $\mathit{O}$ is generated. Let the pixel value at position $(u,v,t)$ be $a_{u,v,t}^{\prime }$, where $\{1\le$ u $\le N_1\}$, $\{1\le$ v $\le N_2\}$, and $\{1\le$ t $\le 3\}$. To decrypt $\mathit{I}$, we calculate exclusive-or operations between $a_{u,v,t}^{\prime }$ and the pseudo-random bits $k_{u,v,t}^{\prime }$ as

$$e_{u,v,t}^{\prime }=a_{u,v,t}^{\prime }\oplus k_{u,v,t}^{\prime }$$

(16)

where $e_{u,v,t}^{\prime }$ is the pixel value of original image $\mathit{O}$, $k_{u,v,t}^{\prime }$ is generated by the same stream cipher scheme as in the image encryption phase using $K_e$. The diagram of watermark extraction and image recovery is demonstrated in Figure 4.

4. Experimental Results and Discussions

To demonstrate the effectiveness and superiority of our scheme, experiments were conducted on six test images sized $512\times 512$: Baboon, Beeflower, Goldgate, Lena, London, and Peppers (see Figure 5). The choice of free parameters is tabulated in

Table 2. Selection of free parameters.

Parameter	$\mathit{\alpha }$	$\mathit{\beta }$	q	n
Value	1	8	4	8

. For simplicity of calculation, $\alpha$ was set to 1 and $\beta$ was set to 8. Thus, $n=\alpha \times \beta =8$. q was 4 because we embedded four bits to each block. The environment of our experiments was based on a personal computer with a 3.2 GHz Intel i5 processor, 4 GB memory, Windows 10 operating system, and Matlab R2016a. In the following subsections, five aspects of experimental results are presented: (1) reversibility; (2) security; (3) embedding capacity; (4) visual quality; and (5) computational complexity. Finally, we give the feature comparisons with related schemes.

To view the result image of each procedure intuitively, we take Figure 5b as an example. Figure 6a shows the original halftone image, and Figure 6b is the corresponding encrypted result $\mathit{I}$. We can observe that principal contents of original image $\mathit{O}$ were effectively masked after encryption. Figure 6c shows the stego image $\mathit{C}$, which is embedded with watermark and displays at 50%. Figure 6d is the recovered image ${\mathit{O}}^{\prime }$, which is exactly the same as the original image $\mathit{O}$.

4.1. Reversibility

The reversibility of an RDH scheme is that the original image can be recovered losslessly from the stego image. In such case, the scheme is reversible. As shown in Section 3.3, our method is a reversible one. To verify whether the recovered image ${\mathit{O}}^{\prime }$ is identical to the original image $\mathit{O}$, we adopted the correlation coefficient r and MSE (mean squared error). The correlation coefficient is widely used in statistical analysis of the correlation between two variables:

$$r({\mathit{O}}^{\prime },\mathit{O})={\displaystyle \frac{{\displaystyle \sum _m}{\displaystyle \sum _n}(O_{m,n}^{\prime }-\overline{O^{\prime }})(O_{m,n}-\overline{O})}{\sqrt{\left({\displaystyle \sum _m}{\displaystyle \sum _n}{(O_{m,n}^{\prime }-\overline{O^{\prime }})}^2\right)\left({\displaystyle \sum _m}{\displaystyle \sum _n}{(O_{m,n}-\overline{O})}^2\right)}}}$$

(17)

where $O_{m,n}^{\prime }$ and $O_{m,n}$ are pixel values at the $(m,n)$ position of recovered image ${\mathit{O}}^{\prime }$ and original image $\mathit{O}$, respectively. $\overline{O^{\prime }}$ and $\overline{O}$ are the mean values of ${\mathit{O}}^{\prime }$ and $\mathit{O}$, respectively. The value of r is limited in the range $[-1,1]$. The closer the value is to 1, the more similar the two images are to each other. Therefore, the value of r is supposed to be 1 if the two images are identical. The MSE between two images ${\mathit{O}}^{\prime }$ and $\mathit{O}$ is defined as

$$MSE({\mathit{O}}^{\prime },\mathit{O})={\displaystyle \frac{1}{N_1{N}_2}}\sum _{m=1}^{N_1}\sum _{n=1}^{N_2}{(O_{m,n}^{\prime }-O_{m,n})}^2$$

(18)

which is zero if ${\mathit{O}}^{\prime }$ and $\mathit{O}$ are identical. The correlation coefficients of original images and recovered images are all 1 s and all the MSE values are 0 s. That is to say, our scheme is reversible.

4.2. Security

The original images and the watermark are encrypted by the stream cipher scheme. As shown in Figure 7, the encrypted images are completely meaningless and it is difficult to infer their original images from them. To assess the security quantitatively, we used correlation coefficient r (Equation (17)) and peak signal-to-noise ratio (PSNR), which is widely used in evaluating the quality of digital images. The PSNR between cover image $\mathit{I}$ and original halftone image $\mathit{O}$ is defined via the mean square error (MSE) by

$$PSNR(\mathit{O},\mathit{I})=10·{log}_{10}{\displaystyle \frac{M_O^2}{MSE(\mathit{O},\mathit{I})}}\left(\mathrm{dB}\right)$$

(19)

where $M_O$ is the maximum possible pixel value of $\mathit{O}$. It is 1 since the pixels of halftone images are represented using 1 bit per sample. The calculation results are consistent with the presentation of Figure 7.

4.3. Embedding Capacity

To evaluate the embedding capacity, the embedding rate $E_r$ was adopted:

$$E_r=\frac{N_e}{N_t}$$

(20)

where $N_e$ and $N_t$ are the number of embedded bits and the total bits of the original halftone image, respectively. We divided the six test images into blocks of the same size of $1\times 8$, and we embedded 4 bits into each block. The embedding capacity $E_c$ of these images was the same:

$$E_c=w\times 4\times 3\times 3=\lfloor \frac{512}{1}\rfloor \times \lfloor \frac{512}{8}\rfloor \times 4\times 3\times 3=1,179,648\left(\mathrm{bits}\right)$$

(21)

where w is the total amount of blocks for each channel image, we embedded three times on each channel image and there were three channel images.

Table 3. Embedding capacity of different sizes of blocks.

Block Size	Block Amount	Size of m	${\mathit{E}}_{\mathit{c}}$	${\mathit{E}}_{\mathit{r}}$
$1\times 8$	98,304	4	1,179,648	1.5
$1\times 8$	98,304	2	589,824	0.75
$4\times 4$	49,152	3	442,368	0.5625
$8\times 8$	12,288	20	737,280	0.9375
$16\times 16$	3072	32	294,912	0.375
$16\times 16$	3072	16	147,456	0.1875
$16\times 16$	3072	8	73,728	0.0938

shows various embedding capacity when several different sizes of blocks were employed. Lower embedding capacity may lead to a higher visual quality of the marked image. If we want to know the content of the image and we directly decrypt the image, the higher is the image quality, the clearer is the image content.

4.4. Quality of the Marked Image

We decrypted the stego image directly and then obtained marked image $\mathit{M}$ (see examples in Figure 8). The different PSNR values of marked images are shown in Figure 9a for the six test images under different embedding capacity. Besides, the structural similarity index (SSIM) was also utilized to evaluate the quality in Figure 9b

$$SSIM(\mathit{M},\mathit{O})={\displaystyle \frac{(2{\mu }_M{\mu }_O+C_1)(2{\sigma }_{MO}+C_2)}{({\mu }_M^2+{\mu }_O^2+C_1)({\sigma }_M^2+{\sigma }_O^2+C2)}}$$

(22)

where ${\mu }_M$, ${\mu }_O$, ${\sigma }_M$, ${\sigma }_O$, and ${\sigma }_{MO}$ are the local means, standard deviations, and cross-covariance for images $\mathit{M}$ and $\mathit{O}$, respectively.

It can be found in the comparison results that, when we adopt a lower capacity such as 73728 bits, the quality of the marked image $\mathit{M}$ will be better.

4.5. Computational Complexity

For the proposed scheme, the computational complexity of encrypting and decrypting pixels is $\mathcal{O}\left(N\right)$ ($\mathcal{O}$ notation is used to classify algorithms according to how their running time or space requirements grow as the input size grows [32].) because they are linear-time algorithms and the running time increases at most linearly with the size N of the image. The computational complexity of embedding and extraction procedure is $\mathcal{O}\left(m{n}^2\right)$ according to Equation (1), where m and n are the length of the embedded bits of each block and the length of each block, respectively.

4.6. Feature Comparisons

In

Table 4. Feature comparisons among the proposed method and related methods

Method	Real Reversible	Embedding Capacity (bits)	Image Type	Application Domain
Zhang [19]	No	Below 4400 [23]	Grayscale continuous-tone	Encrypt
Zhang [21]	Yes	4400	Grayscale continuous-tone	Encrypt
Ma et al. [23]	Yes	131,072	Grayscale continuous-tone	Encrypt
Fu et al. [24]	Yes	416,809	Grayscale continuous-tone	Encrypt
Lien et al. [33]	Yes	79,438	Grayscale halftone	Plaintext
Chen et al. [34]	No	23,814	Grayscale halftone	Plaintext
Jia  et al. [35]	Yes	56,617	Grayscale continuous-tone	Plaintext
Kim et al. [27]	No	4096	Grayscale halftone	Encrypt
Li et al. [36]	Yes	725,000	Color continuous-tone	Plaintext
Ours	Yes	1,179,648	Color halftone	Encrypt

, feature comparisons among the proposed method and other related methods are given. Different from other methods, the carrier images of our method are color halftone images. In addition, our method has real reversibility and provides a high embedding capacity for halftone images, although less redundancy exists in encrypted color halftone images.

5. Conclusions

In this paper, a reversible data hiding scheme for encrypted color halftone images is proposed. As less information redundancy is available for halftone images, we adopted two stego images to add redundancy artificially. This can increase the embedding capacity of the scheme, and, more importantly, the original image can be restored. Moreover, we combine the four stego images generated in embedding procedure into one image for easy transmission. By using two secret keys, the cover image can be recovered losslessly after the watermarks are extracted. Experimental results demonstrate the advantages of our methods. The proposed scheme can realize real reversibility with high embedding capacity for encrypted color halftone images.