Computational Screening of New Perovskite Materials Using Transfer Learning and Deep Learning
Abstract
:1. Introduction
- (1)
- We proposed a transfer learning strategy to convert formation energy related structural features/insights into training data for a perovskite screening model using only elemental Magpie features. This enables us to address the small dataset issue in typical ML based materials discovery.
- (2)
- We developed a gradient boosting regressor (GBR) ML model trained with structural and elemental features for perovskite formation energy prediction, which outperforms the state-of-the-art artificial neural network (ANN) based model trained with two elemental descriptors. This highly accurate model allows us to annotate the large number of material samples with structural information but no formation energy.
- (3)
- We built a convolutional neural network model trained with the enlarged large dataset together with generic Magpie elemental descriptors for large-scale screening of hypothetical perovskites.
- (4)
- Application of our model to a large dataset with 21,316 possible candidates has allowed us to identify interesting stable perovskites available for further experimental or computational density functional theory (DFT) verification.
2. Materials and Methods
2.1. Materials Dataset Preparation and Features
2.1.1. Structural and Elemental Features
2.1.2. Magpie Features
2.2. Overview of Our Data-Driven Framework for Computational Screening
2.3. GBR Machine Learning Model for Formation Energy Prediction
Gradient Boosting Regressor
- max_depth = 6; n_estimators = 500; min_samles_split = 0.5;
- subsample = 0.7; alpha = 0.1; learning_rate = 0.01; loss = ls
2.4. Structure Information Enabled Transfer Learning and CNN Based Screening ML Model
2.4.1. Transfer Learning
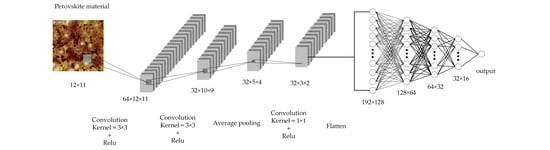
2.4.2. Convolutional Neural Network Model
2.4.3. The Convolutional Neural Network Training Process
2.5. Verification Whether a Screened ABX3 Material is Perovskite or Non-Perovskite
3. Results and Discussions
3.1. Selection of the Best Material Features and Analysis of Feature Importance
3.2. Performance of the M1 Model with Hybrid Structural and Elemental Features
3.3. Performance of M2 Perovskite Screening Model
3.4. Screening Results Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aksel, E.; Jones, J.L. Advances in lead-free piezoelectric materials for sensors and actuators. Sensors 2010, 10, 1935–1954. [Google Scholar] [CrossRef] [PubMed]
- Vinila, V.; Jacob, R.; Mony, A.; Nair, H.G.; Issac, S.; Rajan, S.; Nair, A.S.; Satheesh, D.; Isac, J. Ceramic Nanocrystalline Superconductor Gadolinium Barium Copper Oxide (GdBaCuO) at Different Treating Temperatures. J. Cryst. Process Technol. 2014, 4, 168–176. [Google Scholar] [CrossRef] [Green Version]
- Beno, M.; Soderholm, L.; Capone, D.; Hinks, D.; Jorgensen, J.; Grace, J.; Schuller, I.K.; Segre, C.; Zhang, K. Structure of the single-phase high-temperature superconductor YBa2Cu3O7—δ. Appl. Phys. Lett. 1987, 51, 57–59. [Google Scholar] [CrossRef] [Green Version]
- Laffez, P.; Tendeloo, G.V.; Seshadri, R.; Hervieu, M.; Martin, C.; Maignan, A.; Raveau, B. Microstructural and physical properties of layered manganites oxides related to the magnetoresistive perovskites. J. Appl. Phys. 1996, 80, 5850–5856. [Google Scholar] [CrossRef]
- Maignan, A.; Hébert, S.; Pi, L.; Pelloquin, D.; Martin, C.; Michel, C.; Hervieu, M.; Raveau, B. Perovskite manganites and layered cobaltites: Potential materials for thermoelectric applications. Cryst. Eng. 2002, 5, 365–382. [Google Scholar] [CrossRef]
- Song, K.-S.; Kang, S.-K.; Kim, S.D. Preparation and characterization of Ag/MnO x/perovskite catalysts for CO oxidation. Catal. Lett. 1997, 49, 65–68. [Google Scholar] [CrossRef]
- Suntivich, J.; May, K.J.; Gasteiger, H.A.; Goodenough, J.B.; Shao-Horn, Y. A perovskite oxide optimized for oxygen evolution catalysis from molecular orbital principles. Science 2011, 334, 1383–1385. [Google Scholar] [CrossRef]
- Yuan, M.; Quan, L.N.; Comin, R.; Walters, G.; Sabatini, R.; Voznyy, O.; Hoogland, S.; Zhao, Y.; Beauregard, E.M.; Kanjanaboos, P. Perovskite energy funnels for efficient light-emitting diodes. Nat. Nanotechnol. 2016, 11, 872–877. [Google Scholar] [CrossRef]
- Cho, H.; Jeong, S.-H.; Park, M.-H.; Kim, Y.-H.; Wolf, C.; Lee, C.-L.; Heo, J.H.; Sadhanala, A.; Myoung, N.; Yoo, S. Overcoming the electroluminescence efficiency limitations of perovskite light-emitting diodes. Science 2015, 350, 1222–1225. [Google Scholar] [CrossRef]
- Veldhuis, S.A.; Boix, P.P.; Yantara, N.; Li, M.; Sum, T.C.; Mathews, N.; Mhaisalkar, S.G. Perovskite materials for light-emitting diodes and lasers. Adv. Mater. 2016, 28, 6804–6834. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-S.; Lee, C.-R.; Im, J.-H.; Lee, K.-B.; Moehl, T.; Marchioro, A.; Moon, S.-J.; Humphry-Baker, R.; Yum, J.-H.; Moser, J.E. Lead iodide perovskite sensitized all-solid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%. Sci. Rep. 2012, 2, 6022–6025. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Ri, K.; Mei, A.; Liu, L.; Hu, M.; Liu, T.; Li, X.; Han, H. The size effect of TiO2 nanoparticles on a printable mesoscopic perovskite solar cell. J. Mater. Chem. A 2015, 3, 9103–9107. [Google Scholar] [CrossRef]
- Yang, W.S.; Park, B.-W.; Jung, E.H.; Jeon, N.J.; Kim, Y.C.; Lee, D.U.; Shin, S.S.; Seo, J.; Kim, E.K.; Noh, J.H. Iodide management in formamidinium-lead-halide—Based perovskite layers for efficient solar cells. Science 2017, 356, 1376–1379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, R.; Xiao, K.; Qin, Z.; Han, Q.; Zhang, C.; Wei, M.; Saidaminov, M.I.; Gao, Y.; Xu, J.; Xiao, M. Monolithic all-perovskite tandem solar cells with 24.8% efficiency exploiting comproportionation to suppress Sn (ii) oxidation in precursor ink. Nat. Energy 2019, 4, 864–873. [Google Scholar] [CrossRef]
- Shi, Z.; Jayatissa, A.H. Perovskites-based solar cells: A review of recent progress, materials and processing methods. Materials 2018, 11, 729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ceder, G.; Morgan, D.; Fischer, C.; Tibbetts, K.; Curtarolo, S. Data-mining-driven quantum mechanics for the prediction of structure. MRS Bull. 2006, 31, 981–985. [Google Scholar] [CrossRef] [Green Version]
- Michie, D.; Spiegelhalter, D.J.; Taylor, C. Machine learning. Neural Stat. Classif. 1994, 13, 19–22. [Google Scholar]
- Rajan, K. Materials informatics: The materials “gene” and big data. Annu. Rev. Mater. Res. 2015, 45, 153–169. [Google Scholar] [CrossRef] [Green Version]
- De Luna, P.; Wei, J.; Bengio, Y.; Aspuru-Guzik, A.; Sargent, E. Use machine learning to find energy materials. Nature 2017, 552, 23–27. [Google Scholar] [CrossRef]
- Ferguson, A.L. Machine learning and data science in soft materials engineering. J. Phys. Condens. Matter 2017, 30, 043002. [Google Scholar] [CrossRef] [PubMed]
- Mannodi-Kanakkithodi, A.; Huan, T.D.; Ramprasad, R. Mining materials design rules from data: The example of polymer dielectrics. Chem. Mater. 2017, 29, 9001–9010. [Google Scholar] [CrossRef]
- Saad, Y.; Gao, D.; Ngo, T.; Bobbitt, S.; Chelikowsky, J.R.; Andreoni, W. Data mining for materials: Computational experiments with A B compounds. Phys. Rev. B 2012, 85. [Google Scholar] [CrossRef] [Green Version]
- Seko, A.; Togo, A.; Hayashi, H.; Tsuda, K.; Chaput, L.; Tanaka, I. Prediction of low-thermal-conductivity compounds with first-principles anharmonic lattice-dynamics calculations and Bayesian optimization. Phys. Rev. Lett. 2015, 115. [Google Scholar] [CrossRef]
- Ghiringhelli, L.M.; Vybiral, J.; Levchenko, S.V.; Draxl, C.; Scheffler, M. Big data of materials science: Critical role of the descriptor. Phys. Rev. Lett. 2015, 114. [Google Scholar] [CrossRef] [Green Version]
- Cubuk, E.D.; Sendek, A.D.; Reed, E.J. Screening billions of candidates for solid lithium-ion conductors: A transfer learning approach for small data. J. Chem. Phys. 2019, 150, 214701. [Google Scholar] [CrossRef] [Green Version]
- Emery, A.A.; Wolverton, C. High-throughput dft calculations of formation energy, stability and oxygen vacancy formation energy of abo 3 perovskites. Sci. Data 2017, 4. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, J.; Shi, J.; Borlido, P.; Chen, L.; Botti, S.; Marques, M.A. Predicting the thermodynamic stability of solids combining density functional theory and machine learning. Chem. Mater. 2017, 29, 5090–5103. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Ong, S.P.; Richards, W.D.; Jain, A.; Hautier, G.; Kocher, M.; Cholia, S.; Gunter, D.; Chevrier, V.L.; Persson, K.A.; Ceder, G. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci. 2013, 68, 314–319. [Google Scholar] [CrossRef] [Green Version]
- Ward, L.; Dunn, A.; Faghaninia, A.; Zimmermann, N.E.; Bajaj, S.; Wang, Q.; Montoya, J.; Chen, J.; Bystrom, K.; Dylla, M. Matminer: An open source toolkit for materials data mining. Comput. Mater. Sci. 2018, 152, 60–69. [Google Scholar] [CrossRef] [Green Version]
- Ward, L.; Agrawal, A.; Choudhary, A.; Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater. 2016, 2. [Google Scholar] [CrossRef] [Green Version]
- Ye, W.; Chen, C.; Wang, Z.; Chu, I.-H.; Ong, S.P. Deep neural networks for accurate predictions of crystal stability. Nat. Commun. 2018, 9, 3800. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Stochastic pooling for regularization of deep convolutional neural networks. arXiv 2013, arXiv:1301.3557. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
- Bartel, C.J.; Sutton, C.; Goldsmith, B.R.; Ouyang, R.; Musgrave, C.B.; Ghiringhelli, L.M.; Scheffler, M. New tolerance factor to predict the stability of perovskite oxides and halides. Sci. Adv. 2019, 5. [Google Scholar] [CrossRef] [Green Version]
- Im, J.; Lee, S.; Ko, T.-W.; Kim, H.W.; Hyon, Y.; Chang, H. Identifying Pb-free perovskites for solar cells by machine learning. npj Comput. Mater. 2019, 5. [Google Scholar] [CrossRef] [Green Version]
- Jha, D.; Ward, L.; Paul, A.; Liao, W.-K.; Choudhary, A.; Wolverton, C.; Agrawal, A. Elemnet: Deep learning the chemistry of materials from only elemental composition. Sci. Rep. 2018, 8, 1–13. [Google Scholar] [CrossRef]
- Shin, S.S.; Yeom, E.J.; Yang, W.S.; Hur, S.; Kim, M.G.; Im, J.; Seo, J.; Noh, J.H.; Seok, S.I. Colloidally prepared La-doped BaSnO3 electrodes for efficient, photostable perovskite solar cells. Science 2017, 356, 167–171. [Google Scholar] [CrossRef]
- Mehmood, S.; Ali, Z.; Khan, I.; Khan, F.; Ahmad, I. First-Principles Study of Perovskite Molybdates AMoO 3 (A= Ca, Sr, Ba). J. Electron. Mater. 2019, 48, 1730–1739. [Google Scholar]
- Swarnkar, A.; Marshall, A.R.; Sanehira, E.M.; Chernomordik, B.D.; Moore, D.T.; Christians, J.A.; Chakrabarti, T.; Luther, J.M. Quantum dot–induced phase stabilization of α-CsPbI3 perovskite for high-efficiency photovoltaics. Science 2016, 354, 92–95. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, Y.; Park, C.H.; Matsuishi, K. First-principles study of the Structural and the electronic properties of the lead-Halide-based inorganic-organic perovskites (CH~ 3NH~ 3) PbX~ 3 and CsPbX~ 3 (X= Cl, Br, I). J.-Korean Phys. Soc. 2004, 44, 889–893. [Google Scholar]
- Balena, A.; Perulli, A.; Fernandez, M.; De Giorgi, M.L.; Nedelcu, G.; Kovalenko, M.V.; Anni, M. Temperature Dependence of the Amplified Spontaneous Emission from CsPbBr3 Nanocrystal Thin Films. J. Phys. Chem. C 2018, 122, 5813–5819. [Google Scholar] [CrossRef]
- Swarnkar, A.; Chulliyil, R.; Ravi, V.K.; Irfanullah, M.; Chowdhury, A.; Nag, A. Colloidal CsPbBr3 perovskite nanocrystals: Luminescence beyond traditional quantum dots. Angew. Chem. Int. Ed. 2015, 54, 15424–15428. [Google Scholar] [CrossRef]









| Name | Type | Unit | Description |
|---|---|---|---|
| Chemical formula | string | None | Chemical composition of the compound. The first and second elements correspond to the A- and B-site, respectively. The third element is oxygen |
| Hull distance | number | eV/atom | Hull distance as calculated by the equation of the distortion with the lowest energy. A compound is considered stable if it is within 0.025 eV per atom of the convex hull |
| Bandgap | number | eV | PBE band gap obtained from the relaxed structure |
| X_A | number | eV | The electronegativity of the A atom in the compound |
| X_B | number | eV | The electronegativity of the B atom in the compound |
| X_O | number | eV | The electronegativity of the O atom in the compound |
| A_atomic_mass | number | amu | Atomic mass of atom A |
| B_atomic_mass | number | amu | Atomic mass of atom B |
| O_atomic_mass | number | amu | Atomic mass of atom O |
| A_average_ionic_radius | number | ang | The average is taken over all oxidation states of the A element for which data is present |
| B_average_ionic_radius | number | ang | The average is taken over all oxidation states of the B element for which data is present |
| O_average_ionic_radius | number | ang | The average is taken over all oxidation states of the O element for which data is present |
| minDistA | number | None | Atomic distance between the A cation and the nearest oxygen atom |
| minDistB | number | None | Atomic distance between the B cation and the nearest oxygen atom |
| A_molar_volume | number | mol | molar volume of A element |
| B_molar_volume | number | mol | molar volume of B element |
| O_molar_volume | number | mol | molar volume of O element |
| A_electrical_resistivity | number | ohmm | electrical resistivity of A element |
| B_electrical_resistivity | number | ohmm | electrical resistivity of B element |
| O_electrical_resistivity | number | ohmm | electrical resistivity of O element |
| A_atomic_radius | number | ang | Atomic radius of element A |
| B_atomic_radius | number | ang | Atomic radius of element B |
| O_atomic_radius | number | ang | Atomic radius of element O |
| LUMO | number | eV | The lowest unoccupied molecular orbital |
| HOMO | number | eV | The highest occupied molecular orbital |
| volume | number | Å3 | Volumes of crystal structures. |
| a | number | Å | Lattice parameter a of the relaxed structure |
| b | number | Å | Lattice parameter b of the relaxed structure |
| c | number | Å | Lattice parameter c of the relaxed structure |
| alpha | number | ° | α angle of the relaxed structure. α = 90 for the cubic, tetragonal, and orthorhombic distortion |
| beta | number | ° | β angle of the relaxed structure. β = 90 for the cubic, tetragonal, and orthorhombic distortion |
| gamma | number | ° | γ angle of the relaxed structure. γ = 90 for the cubic, tetragonal, and orthorhombic distortion |
| Descriptors | RMSE | MAE | R2 |
|---|---|---|---|
| Ong_Descriptors | 0.15 | 0.29 | 0.78 |
| Magpie | 0.11 | 0.25 | 0.83 |
| Hybrid_descriptors | 0.08 | 0.20 | 0.88 |
| Regression Model | RMSE | MAE | R2 |
|---|---|---|---|
| SVR | 0.83 | 0.67 | 0.20 |
| RFR | 0.40 | 0.29 | 0.80 |
| Lasso | 0.43 | 0.33 | 0.75 |
| GBR | 0.28 | 0.20 | 0.91 |
| Model | RMSE | MAE | R2 |
|---|---|---|---|
| ElemNet | 0.49 | 0.64 | 0.52 |
| RF | 0.36 | 0.27 | 0.83 |
| GBR | 0.35 | 0.25 | 0.84 |
| CNN | 0.34 | 0.24 | 0.85 |
| Formula | τ | Stability | Formula | τ | Stability | Formula | τ | Stability |
|---|---|---|---|---|---|---|---|---|
| NiPtO3 | −58.1089 | −0.729 | RbPuO3 | 3.4805 | −0.103 | CeRhO3 | 1.3071 | −0.061 |
| KPaO3 | 4.0629 | −0.567 | EuMoO3 | 3.2674 | −0.101 | SmVO3 | 2.9774 | −0.057 |
| RbPaO3 | 3.6251 | −0.543 | KPuO3 | 3.78 | −0.1 | CsNpO3 | 3.3106 | −0.056 |
| LiPaO3 | −5.7739 | −0.311 | SrTcO3 | 3.8734 | −0.097 | SmAlO3 | 1.9819 | −0.054 |
| CsPaO3 | 3.3524 | −0.298 | BaZrO3 | 3.7699 | −0.096 | EuNbO3 | 4.09 | −0.053 |
| BaHfO3 | 3.7284 | −0.247 | EuVO3 | 3.3069 | −0.093 | BaSnO3 | 3.6543 | −0.052 |
| KNbO3 | 3.5401 | −0.221 | AcTiO3 | 3.8113 | −0.092 | NpTiO3 | 3.6701 | −0.051 |
| EuGeO3 | 3.1904 | −0.212 | CeAlO3 | −0.5164 | −0.086 | KTcO3 | 3.555 | −0.048 |
| EuTcO3 | 2.8001 | −0.15 | EuAsO3 | 2.0406 | −0.081 | LiOsO3 | −2.1229 | −0.044 |
| RbNpO3 | 3.5353 | −0.15 | CeMnO3 | −0.9994 | −0.079 | CeGaO3 | 1.8339 | −0.043 |
| EuOsO3 | −65.0247 | −0.143 | AcCuO3 | 3.2679 | −0.077 | EuIrO3 | 3.1159 | −0.043 |
| KNpO3 | 3.8902 | −0.142 | AcNiO3 | 2.3005 | −0.077 | GdAlO3 | 3.1334 | −0.041 |
| NpAlO3 | −20.7485 | −0.129 | LaVO3 | 3.64 | −0.077 | EuCoO3 | 3.1653 | −0.038 |
| EuRhO3 | 2.8422 | −0.128 | PrVO3 | 3.2155 | −0.077 | CeNiO3 | 1.144 | −0.037 |
| AcPdO3 | 3.7105 | −0.122 | EuAlO3 | 2.1447 | −0.075 | YbSiO3 | 1.9755 | −0.032 |
| AcMnO3 | 1.718 | −0.12 | AcGaO3 | 2.4961 | −0.073 | BaTiO3 | 3.7351 | −0.03 |
| AcFeO3 | 3.8271 | −0.116 | LaAlO3 | 2.3073 | −0.072 | DyAlO3 | 2.6055 | −0.03 |
| AcVO3 | 2.6908 | −0.116 | EuPtO3 | 3.7879 | −0.071 | LaGaO3 | 3.3386 | −0.028 |
| EuRuO3 | 2.0471 | −0.112 | NdVO3 | 2.555 | −0.071 | PuGaO3 | −10.427 | −0.028 |
| AcAlO3 | 1.8388 | −0.11 | EuReO3 | 2.472 | −0.067 | YAlO3 | 3.5597 | −0.023 |
| ErAlO3 | 3.699 | −0.022 | SrRhO3 | 3.8864 | −0.006 | KReO3 | 3.584 | 0.008 |
| LaCoO3 | 3.4776 | −0.022 | BaPdO3 | 3.7136 | −0.005 | YbReO3 | 3.6451 | 0.009 |
| NaOsO3 | −11.1333 | −0.021 | KWO3 | 3.5403 | −0.004 | CsUO3 | 3.3037 | 0.01 |
| PuNiO3 | −13.1563 | −0.02 | BaFeO3 | 3.7385 | 0 | EuGaO3 | 3.0439 | 0.013 |
| LaNiO3 | 3.0358 | −0.019 | EuNiO3 | 2.7795 | 0 | SrCoO3 | 3.9892 | 0.014 |
| TmAlO3 | 2.926 | −0.017 | LaMnO3 | 2.1032 | 0 | CeTmO3 | −300.872 | 0.015 |
| SrRuO3 | 3.6809 | −0.013 | EuSiO3 | 1.6849 | 0.001 | DyGaO3 | 3.8882 | 0.017 |
| UAlO3 | −11.2029 | −0.011 | NdMnO3 | 1.6622 | 0.001 | BaPtO3 | 3.5778 | 0.019 |
| YbAlO3 | 3.0372 | −0.011 | SmMnO3 | 1.8354 | 0.001 | DyCoO3 | 4.0617 | 0.02 |
| SmCoO3 | 2.8557 | −0.009 | TbMnO3 | 0.5464 | 0.002 | YMnO3 | 3.1268 | 0.023 |
| SmNiO3 | 2.5241 | −0.009 | EuMnO3 | 1.9694 | 0.003 | DyMnO3 | 2.3484 | 0.024 |
| LuAlO3 | 4.1571 | −0.008 | SmGaO3 | 2.7514 | 0.006 | SrIrO3 | 3.9732 | 0.025 |
| PuVO3 | −7.538 | −0.008 | NaReO3 | 4.1088 | 0.007 |
| Formula | τ | Formula | τ | Formula | τ | Formula | τ |
|---|---|---|---|---|---|---|---|
| YbTlBr3 | −20.162 | CaTlCl3 | −14.381 | CaTlI3 | −14.0108 | PrBO3 | −2.0396 |
| CaTlBr3 | −14.3041 | NaHgCl3 | −13.5492 | TlSnI3 | 2.7082 | LiNdO3 | −2.0303 |
| CrCoBr3 | 1.55 | MgTlCl3 | −6.3625 | TlFeI3 | 2.9924 | LiTeO3 | −1.945 |
| TlGeBr3 | 1.6125 | TlNiCl3 | 1.2386 | CsCrI3 | 3.2934 | TaBeO3 | −1.754 |
| TlFeBr3 | 2.5339 | TlCoCl3 | 1.4647 | CsInI3 | 3.2934 | ThBeO3 | −1.7537 |
| CsFeBr3 | 2.8551 | TlGeCl3 | 1.4794 | CsMgI3 | 3.3089 | CeBeO3 | −1.7537 |
| CsScBr3 | 2.8556 | TlVCl3 | 1.5469 | CsTiI3 | 3.3142 | CrRhO3 | −1.747 |
| CsPdBr3 | 2.8561 | TlCuCl3 | 1.9923 | CsSnI3 | 3.3312 | PuPtO3 | −1.6802 |
| CsPtBr3 | 2.8713 | CsPdCl3 | 2.735 | CsGeI3 | 3.404 | ZrBO3 | −1.6005 |
| CsInBr3 | 2.8777 | CsSnCl3 | 2.7368 | RbTiI3 | 3.4157 | PrBeO3 | −1.5988 |
| CsGeBr3 | 2.8964 | CsCuCl3 | 2.739 | RbSnI3 | 3.4195 | HfBO3 | −1.5526 |
| CsNiBr3 | 2.9272 | CsCoCl3 | 2.7645 | CsYbI3 | 3.4316 | TbSiO3 | −1.4989 |
| RbCuBr3 | 2.9466 | CsCrCl3 | 2.7686 | CsTmI3 | 3.4519 | SnBO3 | −1.4453 |
| RbSnBr3 | 2.9486 | CsInCl3 | 2.7686 | RbVI3 | 3.4526 | CuBO3 | −1.3853 |
| RbVBr3 | 2.9499 | BaNiCl3 | 2.8079 | RbCrI3 | 3.4599 | HgRhO3 | −1.2912 |
| RbGeBr3 | 2.9525 | RbGeCl3 | 2.8194 | RbInI3 | 3.4599 | GeBO3 | −1.0071 |
| RbCoBr3 | 2.9532 | RbCuCl3 | 2.8216 | RbCrI3 | 3.4599 | PaCoO3 | −1.0055 |
| RbPdBr3 | 2.9543 | RbSnCl3 | 2.8251 | RbGeI3 | 3.4601 | LiLaO3 | −2.8329 |
| RbTiBr3 | 2.9568 | RbPdCl3 | 2.8331 | CsPbI3 | 3.5094 | HgIrO3 | −0.9862 |
| CsAuBr3 | 3.0427 | RbFeCl3 | 2.8369 | CsDyI3 | 3.5292 | HgGeO3 | −0.9036 |
| RbInBr3 | 3.0441 | RbMgCl3 | 2.8421 | CsCaI3 | 3.5514 | CeAsO3 | −0.8 |
| KGeBr3 | 3.0488 | RbScCl3 | 2.8635 | KSnI3 | 3.5609 | TbBeO3 | −0.7902 |
| CsYbBr3 | 3.0711 | KCoCl3 | 2.9149 | KTiI3 | 3.5761 | MnSiO3 | −0.7002 |
| CsAgBr3 | 3.0767 | KGeCl3 | 2.9156 | CsMnI3 | 3.6832 | CoSiO3 | −2.4934 |
| CsCdBr3 | 3.0839 | KVCl3 | 2.9194 | KInI3 | 3.7193 | BiMoO3 | −0.2924 |
| ZrSiO3 | 0.0224 | EuMnO3 | 1.9694 | GdBO3 | 2.2335 | TmMnO3 | 2.6111 |
| ThReO3 | 0.3455 | ThSiO3 | −2.1251 | GdBeO3 | 2.2465 | PmRuO3 | 2.6249 |
| NpTaO3 | −4.4473 | NpSnO3 | −2.2195 | HoBO3 | 2.2479 | BeAgO3 | −4.6185 |
| CuSiO3 | 0.8738 | NdReO3 | 1.986 | YBO3 | 2.2485 | TlSbO3 | 2.6921 |
| BiRhO3 | −2.1807 | GdSiO3 | 2.0075 | EuBO3 | 2.2486 | SmGaO3 | 2.7514 |
| LiSmO3 | −2.3252 | TlGaO3 | 2.0255 | ErBO3 | 2.2548 | InSiO3 | 2.7544 |
| TlSiO3 | 1.5291 | LiEuO3 | −2.5704 | SmBO3 | 2.2647 | LiCdO3 | −4.1549 |
| NdBeO3 | 1.5459 | BeAuO3 | −4.675 | LuBO3 | 2.2789 | BePbO3 | −4.5119 |
| AcSiO3 | 1.5949 | PmBeO3 | 2.0662 | AcBO3 | 2.285 | AgAsO3 | 2.815 |
| ZrBeO3 | 1.6089 | TlWO3 | 2.0764 | VSiO3 | -2.9169 | AgRuO3 | 2.8273 |
| SmSiO3 | 1.6357 | ThWO3 | 2.0875 | LiPmO3 | -3.731 | LiGdO3 | −4.5398 |
| SmBeO3 | 1.6514 | TlCoO3 | 2.0895 | LuSiO3 | 2.3438 | SmCoO3 | 2.8557 |
| LiYbO3 | −4.301 | TlGeO3 | 2.1027 | TlBO3 | 2.3453 | SmGeO3 | 2.8773 |
| BeHgO3 | −4.2571 | BeOsO3 | −4.2343 | DyMnO3 | 2.3484 | GdAsO3 | 2.9255 |
| BeCdO3 | −4.6077 | TmBeO3 | 2.1393 | CrGeO3 | 2.3535 | BeInO3 | −5.3548 |
| EuBeO3 | 1.7345 | HoSiO3 | 2.1444 | ThMoO3 | 2.423 | TlFeO3 | 2.9768 |
| CrWO3 | 1.7353 | LiCaO3 | −3.2345 | HoBeO3 | 2.4577 | SmVO3 | 2.9774 |
| LaBeO3 | 1.8183 | BiPtO3 | 2.145 | LiTmO3 | −4.0403 | LiPrO3 | −5.0002 |
| CrTcO3 | −2.2119 | YSiO3 | 2.1489 | NdGeO3 | 2.4752 | YbAlO3 | 3.0372 |
| LiCeO3 | −4.404 | LaAsO3 | 2.1864 | LiDyO3 | −3.369 | EuGaO3 | 3.0439 |
| BeBiO3 | −4.8111 | YbBeO3 | 2.1968 | SmNiO3 | 2.5241 | GaBO3 | 3.0837 |
| TiBeO3 | 1.8655 | DyBO3 | 2.2289 | ErBeO3 | 2.535 | NdTaO3 | 3.0888 |
| TlNiO3 | 1.8873 | TmBO3 | 2.2293 | FeAsO3 | −3.8096 | HgRuO3 | −2.1943 |
| TlTcO3 | 1.898 | AgBO3 | 2.2307 | TlCuO3 | 2.5776 | HoMnO3 | 3.1159 |
| HfBeO3 | 1.9189 | YbBO3 | 2.2312 | LiAcO3 | −2.1229 | ThBO3 | −2.0482 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Dan, Y.; Dong, R.; Cao, Z.; Niu, C.; Song, Y.; Li, S.; Hu, J. Computational Screening of New Perovskite Materials Using Transfer Learning and Deep Learning. Appl. Sci. 2019, 9, 5510. https://doi.org/10.3390/app9245510
Li X, Dan Y, Dong R, Cao Z, Niu C, Song Y, Li S, Hu J. Computational Screening of New Perovskite Materials Using Transfer Learning and Deep Learning. Applied Sciences. 2019; 9(24):5510. https://doi.org/10.3390/app9245510
Chicago/Turabian StyleLi, Xiang, Yabo Dan, Rongzhi Dong, Zhuo Cao, Chengcheng Niu, Yuqi Song, Shaobo Li, and Jianjun Hu. 2019. "Computational Screening of New Perovskite Materials Using Transfer Learning and Deep Learning" Applied Sciences 9, no. 24: 5510. https://doi.org/10.3390/app9245510
APA StyleLi, X., Dan, Y., Dong, R., Cao, Z., Niu, C., Song, Y., Li, S., & Hu, J. (2019). Computational Screening of New Perovskite Materials Using Transfer Learning and Deep Learning. Applied Sciences, 9(24), 5510. https://doi.org/10.3390/app9245510