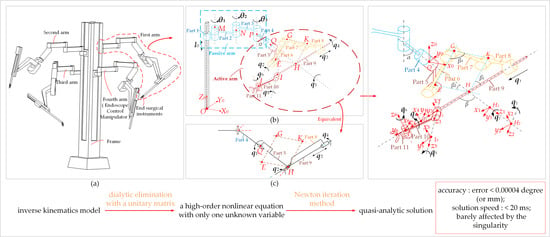
Solving the Time-Varying Inverse Kinematics Problem for the Da Vinci Surgical Robot

Featured Application

The work of this paper is mainly applied for the inverse kinematics solving of Da Vinci surgical robot and its similar robotic systems that do not satisfy the Pieper principle.

Abstract

A dialytic-elimination and Newton-iteration based quasi-analytic inverse kinematics approach is proposed for the 6 degree of freedom (DOF) active slave manipulator in the Da Vinci surgical robot and other similar systems. First, the transformation matrix-based inverse kinematics model is derived; then, its high-dimensional nonlinear equations are transformed to a high-order nonlinear equation with only one unknown variable by using the dialytic elimination with a unitary matrix. Finally, the quasi-analytic solution is eventually obtained by the Newton iteration method. Simulations are conducted, and the result show that the proposed quasi-analytic approach has advantages in terms of accuracy (error < 0.00004 degree (or mm)), solution speed (<20 ms) and is barely affected by the singularity during intermediate calculations, which proves that the approach meets the real-time and high-accuracy requirements of master–slave mapping control for the Da Vinci surgical robots and other similar systems. In addition, the proposed approach can also serve as a design reference for other types of robotic arms that do not satisfy the Pieper principle.

1. Introduction

In recent years, medical robots have increasingly been used as fundamental surgical instrument/equipment [1], among which the Da Vinci system developed by Intuitive Surgical Company is the most successful [2]. The Da Vinci robotic system consists of three components: the surgeon console (master manipulators), the patient trolley (slave manipulators), and the imaging system [3]. The surgeon manipulates two master handles at the master remote console, which can acquire high-resolution, binocular, three-dimensional, magnified views of the operative field as compared with open surgery [4]. However, this kind of master–slave operation mode poses a great challenge to the real-time and accurate performance of the master–slave mapping control, among which the inverse kinematics problem is the first obstacle. The Da Vinci system and similar surgical robot systems satisfy the following two features:

(1)

contain mechanical structures to generate Remote Center of Motion [5] (RCM, a fixed point on the active arm, there are two methods to generate RCM based motion: (a) virtual RCM, (b) physically constrained RCM [6]), and the structure can be simplified;

(2)

do not satisfy the Pieper principle.

At present, the main methods of robotic inverse kinematics include the analytic method and the numerical method. The analytic approach uses vector, spinor or Lie algebra to obtain results [7,8,9], which can only obtain satisfied solutions in limited robotic configurations that should satisfy the Pieper principle [10,11], etc. However, to imitate the surgeon operation, the manipulators of most thoracic and abdominal surgery robots, including the Da Vinci system, contain rotational/translational kinematic pairs, tilt angle joints, and offset joints at the tip (artificial wrist part) that are designed for additional flexibility, which is beyond the solution capability of the analytic approach.

One feasible strategy is to simplify the kinematic model to acquire analytical results. For example, Ai et al. and Podsedkowski et al. [12,13] obtained an approximate solution by separating the position and orientation of the slave manipulators, the solution deviation of which needs to be manually eliminated by experienced surgeons via visual inspection. Zhang et al. [14] solved the inverse kinematics of a 4-DOF surgical robot using the elimination method, and Mezouar et al. [15] used unit dual quaternions to model the kinematics, however, outcomes of their studies benefited strongly from the simplicity of the arm configuration. In addition, Fu et al. [16,17] obtained an approximate solution based on the differential transformation that increases error feedbacks to compensate the cumulative error, the final precision of which can reach 0.18 mm.

Another way to solve the inverse kinematics problem of the surgical robot that does not satisfy the Pieper principle is the Jacobian matrix-based numerical method [18]. However, this method involves a Jacobian matrix, which may lose versatility due to its singularity problem as well as the low convergence speed of the iterative solutions. To improve the numerical solution performance, a numerical method based on the position increment of robotic joints was proposed [18]. Specifically, to make this method suitable for the inverse kinematics analysis of a robotic manipulator with an offset wrist, Bu et al. [19] used the method of decoupling DOFs based on a cut-off point that is limited by the manipulator configuration. In addition, modern methods such as the neural network method [20], the genetic algorithm [21], the electromagnetism-like mechanism [22,23], the hybrid electromagnetism-like mechanism [24], etc., have been gradually explored for possible solutions of the inverse kinematics of surgical robots. However, these methods either require a large amount of sample data or suffer from poor convergence speed; therefore, these methods are not suitable for the rapid development of a master–slave manipulator in surgical robots.

To address the lack of efficient and accurate inverse kinematics solutions for the Da Vinci system, we propose a quasi-analytic solution method that involves dialytic elimination and the Newton iteration method. The dialytic elimination method [25] is used to transform the high-dimensional equations into a nonlinear equation containing only one unknown variable, which is then solved by the Newton iteration method. In applying this method to the inverse kinematics solution of slave manipulator, we show dual superiorities: (a) barely affected by the singularity problem and (b) maintain rapidity.

The steps of our proposed method as follows:

(1)

simplify the structure of RCM, using an equivalent mechanism to take the place of the RCM mechanism.

(2)

establish the coordinate system, this step can be realized by the D–H (Denavit–Hartenberg) method or combine the characteristics of the structure to make sure there are more origins of the coordinate system can be set up at the same point.

(3)

obtain the mathematical model of forward and inverse kinematics via the matrix transformation method. Then, transform the high-dimensional equations into a nonlinear equation containing only one unknown parameter using the dialytic elimination method, and solve it by the Newton iteration method.

The rest of this paper is organized as follows: Section 2 presented the kinematics analysis of the Da Vinci system; Section 3 solves the inverse kinematics by the Newton iteration method; Section 4 analyzes our solution and compared it with other methods via a simulation; Section 5 concludes the paper.

2. Kinematics Analysis

2.1. Forward Kinematics Analysis

During surgery using the Da Vinci medical robot, dual articulated arms (slave manipulators) work as the right and left hand of the surgeon, respectively. The coordinate frame of the master/slave manipulator is set the same as the coordinate frame of human sight, i.e., the world coordinate frame. Therefore, in Figure 1, the origin of the base coordinate frame of the slave manipulator is located at the bottom of the robot frame. The Z₀-axis is upward, along the robot frame.

Before surgery, the angles of passive joints M, N, and P and the position of the M joint on the frame are adjusted manually and then remain fixed during surgery. The joints that mainly assist the surgeon are the active joints of the slave manipulator: Q, E, G, K, H, I, and J in Figure 1b.

The DOFs of the slave manipulator includes four DOFs: l₀, θ₁, θ₂ and θ₃. The parts 6, 7, and 8 in the active arm belong to the parallelogram mechanism (i.e., these three parts cannot move freely but under the motion constraint of the parallelogram mechanism in Figure 1c. Then only parts 4, 5, 8 and 9 can move freely in the slave manipulator, i.e., part 5 rotates around part 4, there is rotation between part 6 and part 5, and there is rotation between part 9 and part 8. Therefore, the entire slave manipulator will have 6 DOFs when the additional 3 DOFs of the H joint are considered.

2.2. Mathematical Model of Forward Kinematics

According to the previous analysis, an active arm coordinate system is established in Figure 2. The origin of the base coordinate x₀y₀z₀ (0-coordinate frame) of the active arm is established at the joint Q between the passive and active arms, the direction of which is the same as that of the frame coordinate X₀Y₀Z₀.

Figure 2 shows the six DOFs of the active arm in the slave manipulator, namely five rotating joints: q₁, q₂, q₄, q₅, q₆, and a translational joint: q₃.

Six transform matrixes frame from x₁y₁z₁ (1-coordinate frame) to x₆y₆z₆ (6-coordinate frame) can be obtained as follows:

$$\{\begin{array}{c}\mathit{T}={\left\{-\left(\pi -\alpha \right)\right\}}_x{\left\{{\mathit{q}}_1\right\}}_z{\left\{l_{QH}\right\}}^z\\ {}_2^1\mathit{T}={\left\{-\left(\beta -\frac{\pi }{2}\right)\right\}}_x{\left\{\frac{\pi }{2}\right\}}_y{\left\{{\mathit{q}}_2\right\}}_z\\ {}_3^2\mathit{T}={\left\{{\mathit{q}}_3\right\}}^y\\ {}_4^3\mathit{T}={\left\{-\frac{\pi }{2}\right\}}_x{\left\{{\mathit{q}}_4\right\}}_z\\ {}_5^4\mathit{T}={\left\{\frac{\pi }{2}\right\}}_x{\left\{{\mathit{q}}_5\right\}}_z\\ {}_6^5\mathit{T}={\left\{l_{IJ}\right\}}^y{\left\{\frac{\pi }{2}\right\}}_y{\left\{{\mathit{q}}_6\right\}}_z\end{array},$$

(1)

where ⁱ_jT means transform matrix from the i-coordinate frame to the j-coordinate frame; { }_x, { }_y and { }_z represent the rotation angle around the x-axis, y-axis and z-axis, respectively; { }^x, { }^y and { }^z denotes the translational movement along the x-axis, y-axis and z-axis, respectively.

Then, the pose matrix of the active arm at the endpoint of the slave manipulator can be obtained as follows:

$${}_6{}^0\mathit{T}={}_1{}^0\mathit{T}{}_2{}^1\mathit{T}{}_3{}^2\mathit{T}{}_4{}^3\mathit{T}{}_5{}^4\mathit{T}{}_6{}^5\mathit{T}=\left[\begin{array}{cccc}{n}_x& o_x& a_x& p_x\\ n_y& o_y& a_y& p_y\\ n_z& o_z& a_z& p_z\\ 0& 0& 0& 1\end{array}\right]=\left[\begin{array}{cc}\mathit{R}& \mathit{P}\\ \mathbf{0}& 1\end{array}\right],$$

(2)

where R and P are the orientation and position of the slave manipulator endpoint, respectively. Substituting Equation (1) into Equation (2) yields Equation (3):

$${}_6{}^0\mathit{T}={\left\{-\left(\pi -\alpha \right)\right\}}_x{\left\{{\mathit{q}}_1\right\}}_z{\left\{l_{QH}\right\}}^z{\left\{-\left(\beta -\frac{\pi }{2}\right)\right\}}_x{\left\{\frac{\pi }{2}\right\}}_y{\left\{{\mathit{q}}_2\right\}}_z{\left\{{\mathit{q}}_3\right\}}^y{\left\{-\frac{\pi }{2}\right\}}_x{\left\{{\mathit{q}}_4\right\}}_z{\left\{\frac{\pi }{2}\right\}}_x{\left\{{\mathit{q}}_5\right\}}_z{\left\{l_{IJ}\right\}}^y{\left\{\frac{\pi }{2}\right\}}_y{\left\{{\mathit{q}}_6\right\}}_z.$$

(3)

2.3. Mathematical Model of Inverse Kinematics

In the case of inverse kinematics, the known pose matrix is ⁰₆T in Equation (3), and the unknowns are q₁, q₂, q₃, q₄, q₅ and q₆.

Left-multiplying the matrices $\mathit{T}={\left\{{\mathit{q}}_3\right\}}^{y^{-1}}{\left\{{\mathit{q}}_2\right\}}_z^{-1}{\left\{\frac{\pi }{2}\right\}}_y^{-1}{\left\{-\left(\beta -\frac{\pi }{2}\right)\right\}}_x^{-1}{\left\{l_{QH}\right\}}^{z^{-1}}{\left\{{\mathit{q}}_1\right\}}_z^{-1}{\left\{-\left(\pi -\alpha \right)\right\}}_x^{-1}$ on both sides of Equation (3) yields Equation (4):

$$\mathit{T}{}_6{}^0\mathit{T}={\left\{-\frac{\pi }{2}\right\}}_x{\left\{{\mathit{q}}_4\right\}}_z{\left\{\frac{\pi }{2}\right\}}_x{\left\{{\mathit{q}}_5\right\}}_z{\left\{l_{IJ}\right\}}^y{\left\{\frac{\pi }{2}\right\}}_y{\left\{{\mathit{q}}_6\right\}}_z.$$

(4)

To simplify the complexity of the formula, we construct a unitary matrix [26] U as follows. After introducing the matrix U, the variables in the ⁰₆T can be replaced by the Euler formula.

$$\mathit{U}=\left[\begin{array}{cccc}\frac{1}{\sqrt{2}}i& -\frac{1}{\sqrt{2}}i& 0& 0\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

(5)

In addition, we know that E = U⁻¹U. Left-multiply the inverse of unitary matrix U⁻¹ and right-multiply the matrix U on both sides of Equation (4). Then, multiply the E matrix between these two matrices to transform Equation (4) into the following:

$${\mathit{Y}}_{\mathbf{3}}{\mathit{X}}_{\mathbf{2}}{\mathit{C}}_{\mathbf{1}}{\mathit{X}}_{\mathbf{1}}{\mathit{C}}_{\mathbf{2}}{\mathit{C}}_{\mathbf{3}}={\mathit{C}}_{\mathbf{4}}{\mathit{X}}_{\mathbf{4}}{\mathit{C}}_{\mathbf{5}}{\mathit{X}}_{\mathbf{5}}{\mathit{C}}_{\mathbf{6}}{\mathit{X}}_{\mathbf{6}}.$$

(6)

Here, C₁ = U⁻¹[{l_QH}^z{π/2 − β}_z]⁻¹U, C₂ = U⁻¹[{α − π}_x]⁻¹U, C₃ = U⁻¹⁰₆TU, C₄ = U⁻¹{−π/2}_zU, C₅ = U⁻¹{π/2}_zU, and C₆ = U⁻¹{l_IJ}^y{π/2}_yU. Clearly, C₁, C₂, C₃, C₄, C₅ and C₆ are constant matrices or parameter matrices related to the structure of the robot. In addition, X_j (j = 1, 2, 4, 5, 6) is as follows:

$${\mathit{X}}_j=\{\begin{array}{ll}{\mathit{T}}_{Xj}^{-1}& j=1,2\\ {\mathit{T}}_{Xj}& j=4,5,6\end{array},$$

(7)

where T_Xj (j = 1, 2, 4, 5, 6) represents the results of the transform matrix of q_j rotating around the z-axis, which undergoes the left-multiplication of U⁻¹ and right-multiplication of U. Let x_j = cos(q_j) + isin(q_j), x_j⁻¹ = cos(q_j) − isin(q_j); thus, T_Xj can be expressed as follows:

$${\mathit{T}}_{Xj}={\mathit{U}}^{-1}{\left\{{\mathit{q}}_i\right\}}_z\mathit{U}=\left[\begin{array}{cccc}{\mathit{x}}_j& 0& 0& 0\\ 0& {\mathit{x}}_j^{-1}& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right].$$

(8)

Let Y_j represents the result of the transform matrix q_j along the y-axis, which undergoes the left-multiplication of U⁻¹ and right-multiplication of U, and x_j = q_j; then, Y_j can be expressed as follows:

$$Y_j={\mathit{U}}^{-1}{\left\{{\mathit{q}}_i\right\}}^{\mathrm{y}}\mathit{U}=\left[\begin{array}{cccc}1& 0& 0& -\frac{\sqrt{2}}{2}{\mathit{x}}_j\\ 0& 1& 0& -\frac{\sqrt{2}}{2}{\mathit{x}}_j\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right].$$

(9)

Take $\mathit{A}={\mathit{Y}}_{\mathbf{3}}{\mathit{X}}_{\mathbf{2}}{\mathit{C}}_{\mathbf{1}}{\mathit{X}}_{\mathbf{1}}{\mathit{C}}_{\mathbf{2}}{\mathit{C}}_{\mathbf{3}}$, $\mathit{B}={\mathit{C}}_{\mathbf{4}}{\mathit{X}}_{\mathbf{4}}{\mathit{C}}_{\mathbf{5}}{\mathit{X}}_{\mathbf{5}}{\mathit{C}}_{\mathbf{6}}{\mathit{X}}_{\mathbf{6}}$. Then the dimensions of matrix A and matrix B are both 4 × 4. Each element in matrix A is a function containing x₁, x₂, and x₃, while the elements in matrix B are functions containing x₄, x₅, and x₆. In addition, corresponding elements in matrix A and matrix B are equal, i.e., Aij = Bij. The specific contents of the elements are detailed in Appendix A.

To realize element elimination, we evaluated elements in matrix A and B that do not contain x₆ and x₆⁻¹: B₁₃, B₁₄, B₂₃, B₂₄, B₃₃ and B₃₄ to establish Equation (10):

$$\begin{array}{l}{\mathit{A}}_{13}={\mathit{B}}_{13}\\ {\mathit{A}}_{14}={\mathit{B}}_{14}\\ {\mathit{A}}_{23}={\mathit{B}}_{23}\\ {\mathit{A}}_{24}={\mathit{B}}_{24}\\ {\mathit{A}}_{33}={\mathit{B}}_{33}\\ {\mathit{A}}_{34}={\mathit{B}}_{34}\end{array}\}.$$

(10)

To further eliminate x₄ and x₅, the linear combination of x₄ and x₅, and their reciprocals are treated as new variables, i.e., X = [x₄x₅, x₄x₅⁻¹, x₄⁻¹x₅, x₄⁻¹x₅⁻¹, x₄⁻¹, x₅⁻¹, x₄, x₅, x₄⁰x₅⁰]^T, which contains nine variables. Because there are only six equations in Equation (10), three more equations are required, which are attainable by conducting nonlinear computations on the elements in Equation (10), as shown in Equation (11).

$$\begin{array}{l}{\mathit{A}}^{L1}=-{\mathit{A}}_{34}{\mathit{A}}_{23}+{\mathit{A}}_{24}{\mathit{A}}_{33}=-{\mathit{B}}_{34}{\mathit{B}}_{23}+{\mathit{B}}_{24}{\mathit{B}}_{33}={\mathit{B}}^{L1}\\ {\mathit{A}}^{L2}=-{\mathit{A}}_{24}{\mathit{A}}_{13}+{\mathit{A}}_{14}{\mathit{A}}_{23}=-{\mathit{B}}_{24}{\mathit{B}}_{13}+{\mathit{B}}_{14}{\mathit{B}}_{23}={\mathit{B}}^{L2}\\ {\mathit{A}}^{L3}=-{\mathit{A}}_{13}{\mathit{A}}_{34}+{\mathit{A}}_{14}{\mathit{A}}_{33}=-{\mathit{B}}_{13}{\mathit{B}}_{34}+{\mathit{B}}_{14}{\mathit{B}}_{33}={\mathit{B}}^{L3}\end{array}\}$$

(11)

Then, by combining Equations (10) and (11):

$${\left[\mathit{D}\left({\mathit{x}}_1,{\mathit{x}}_2,{\mathit{x}}_3\right)\right]}_{9\times 9}\mathit{X}=0.$$

(12)

The matrix [D(x₁, x₂, x₃)]_9×9 contains only the variables x₁, x₂, and x₃ since X is nonzero. The condition that Equation (12) has a solution is that the determinant of [D(x₁, x₂, x₃)]_9×9 equals zero. The following equation, which contains x₁, x₂, and x₃, can be obtained provided that |D(x₁, x₂, x₃)| = 0:

$$\left({\mathit{C}}_1^{\prime }{\mathit{x}}_1+{\mathit{C}}_2^{\prime }+{\mathit{C}}_3^{\prime }{\mathit{x}}_1^{-1}\right)x_2=-\left({\mathit{C}}_4^{\prime }{\mathit{x}}_1+{\mathit{C}}_5^{\prime }+{\mathit{C}}_6^{\prime }{\mathit{x}}_1^{-1}\right){\mathit{x}}_2^{-1},$$

(13)

where C’_j is a constant related to the robot’s parameters. Considering that x₁, x₂, x₄, x₅, and x₆ can be defined as x_j = cos(q_j) + isin(q_j) and x_j⁻¹ = cos(q_j) − isin(q_j), then x₁, x₂, x₄, x₅, and x₆ are all non-zero. Therefore, x₂ can be expressed by x₁ according to Equation (13):

$${\mathit{x}}_2^2=\frac{-\left({\mathit{X}}_{\mathbf{1}}^{\prime }{\mathit{x}}_1+{\mathit{C}}_{\mathbf{2}}^{\prime }+{\mathit{C}}_3^{\prime }{\mathit{x}}_1^{-1}\right)}{\left[\left({\mathit{C}}_{\mathbf{4}}^{\prime }{\mathit{x}}_1+{\mathit{C}}_{\mathbf{5}}^{\prime }+{\mathit{C}}_{\mathbf{6}}^{\prime }{\mathit{x}}_1^{-1}\right)\right]}=f_1\left({\mathit{x}}_1\right).$$

(14)

To represent x₃ by x₁ and x₂, we construct the equations A^L4 = A₂₃A₁₄ + A₁₃A₂₄ + A₃₃A₃₄ and B^L4 = B₂₃B₁₄ + B₁₃B₂₄ + B₃₃B₃₄. Let A^L4 = B^L4, then

$$\left({\mathit{C}}_{\mathbf{7}}^{\prime }{\mathit{x}}_1+{\mathit{C}}_{\mathbf{9}}^{\prime }+{\mathit{C}}_{\mathbf{12}}^{\prime }{\mathit{x}}_1^{-1}\right)x_3{x}_2+\left({\mathit{C}}_{\mathbf{8}}^{\prime }{\mathit{x}}_1+{\mathit{C}}_{\mathbf{11}}^{\prime }+{\mathit{C}}_{\mathbf{13}}^{\prime }{\mathit{x}}_1^{-1}\right){\mathit{x}}_3{\mathit{x}}_2^{-1}+{\mathit{C}}_{\mathbf{10}}^{\prime }=0.$$

(15)

Equation (15) contains only three variables, x₁, x₂, and x₃, therefore, x₃ can be expressed by x₁ and x₂ as:

$${\mathit{x}}_3=f_2\left({\mathit{x}}_1,{\mathit{x}}_2\right).$$

(16)

Because both A^L2 and A^L3 are functions of x₁, x₂ and x₃, by combining A^L2 = B^L2 with A^L3 = B^L3, the following can be obtained:

$$\left[\begin{array}{c}{\mathit{x}}_4\\ {\mathit{x}}_4^{-1}\end{array}\right]=\left[\begin{array}{cc}-\frac{i}{l_{IJ}}& -\frac{\sqrt{2}i}{l_{IJ}}\\ -\frac{i}{l_{IJ}}& \frac{\sqrt{2}i}{l_{IJ}}\end{array}\right]\left[\begin{array}{c}{\mathit{A}}^{L2}\\ {\mathit{A}}^{L3}\end{array}\right].$$

(17)

Therefore,

$${\mathit{x}}_4=-\frac{i}{l_{IJ}}{\mathit{A}}^{L2}-\frac{\sqrt{2}i}{l_{IJ}}{\mathit{A}}^{L3}=f_3\left({\mathit{x}}_1,{\mathit{x}}_2,{\mathit{x}}_3\right).$$

(18)

Similarly, by combining A₁₃ = B₁₃ and A₁₄ = B₁₄ with Equation (16), the following can be obtained:

$$\left[\begin{array}{c}{\mathit{x}}_5\\ {\mathit{x}}_5^{-1}\end{array}\right]=\left[\begin{array}{cc}-\frac{\sqrt{2}}{\left({\mathit{A}}^{L2}i-l_{IJ}\right)}& -\frac{\sqrt{2}i{l}_{IJ}}{\left({\mathit{A}}^{L2}i-l_{IJ}\right)}\\ -\frac{\sqrt{2}i}{\left({\mathit{A}}^{L2}-l_{IJ}i\right)}& -\frac{\sqrt{2}{l}_{IJ}}{\left({\mathit{A}}^{L2}-l_{IJ}i\right)}\end{array}\right]\left[\begin{array}{c}{\mathit{A}}_{14}\\ {\mathit{A}}_{13}\end{array}\right].$$

(19)

Therefore, x₅ can be represented by x₁, x₂, and x₃:

$${\mathit{x}}_5=-\frac{\sqrt{2}{\mathit{A}}_{14}}{\left({\mathit{A}}^{L2}i-l_{IJ}\right)}-\frac{\sqrt{2}i{l}_{IJ}{\mathit{A}}_{13}}{\left({\mathit{A}}^{L2}i-l_{IJ}\right)}=f_4\left({\mathit{x}}_1,{\mathit{x}}_2,{\mathit{x}}_3\right).$$

(20)

Combined with Equations (16) to (20) and A₁₁ = B₁₁, x₆ can finally be represented by x₁:

$${\mathit{x}}_6=\frac{\left(b_{1}i+b_2\right){\mathit{x}}_1{\mathit{x}}_2^{-1}+\left(b_{3}i+b_4\right){\mathit{x}}_2^{-1}+\left(b_{5}i+b_6\right){\mathit{x}}_1^{-1}{\mathit{x}}_2^{-1}}{\frac{1}{8}{\mathit{x}}_5{\mathit{x}}_4+\frac{i}{4}{\mathit{x}}_4-\frac{1}{8}{\mathit{x}}_5^{-1}{\mathit{x}}_4+\frac{1}{4}{\mathit{x}}_5+\frac{1}{4}{\mathit{x}}_5^{-1}+\frac{1}{8}{\mathit{x}}_5{\mathit{x}}_4^{-1}-\frac{i}{4}{\mathit{x}}_4^{-1}-\frac{1}{8}{\mathit{x}}_5^{-1}{\mathit{x}}_4^{-1}}=f_5\left({\mathit{x}}_1\right),$$

(21)

where b_j is a constant related to the robot’s parameters.

From Equations (16) to (21), the variables x₂, x₃, x₄, x₅, and x₆ can be represented with the variable x₁. Let A₂₄ and B₂₄ be equal, then:

$$F\left({\mathit{x}}_1\right)={\mathit{A}}_{24}-{\mathit{B}}_{24}=0.$$

(22)

By solving Equation (22), x₁ can be solved, then x₂, x₃, x₄, x₅, and x₆ can be subsequently solved by Equation (16) to (21). Specifically, we know from Equation (14) that ${\mathit{x}}_2=\pm \sqrt{f_1\left({\mathit{x}}_1\right)}$, therefore, F(x₁) will have two expressions:

$$F\left({\xi }_1\right)=\{\begin{array}{l}{F}_1\left({\mathit{x}}_1\right){\mathit{x}}_2=\sqrt{f_1\left({\mathit{x}}_1\right)}\\ F_2\left({\mathit{x}}_1\right){\mathit{x}}_2=-\sqrt{f_1\left({\mathit{x}}_1\right)}\end{array}.$$

(23)

Equation (23) will be electively solved according to the minimum norm of the distance the joint moved.

3. Inverse Kinematics Solution

From the derivation of the forward and inverse kinematics of the Da Vinci slave manipulator, it is known that the key to solving inverse kinematics is to solve the nonlinear Equation (22).

3.1. Inverse Kinematics Solution Method

The Newton–Raphson method is an efficient numerical iterative approach to solve nonlinear equations in real and complex domains. In this paper, we construct the following iterative formula:

$${\mathit{x}}_{n+1}={\mathit{x}}_n-\frac{F\left({\mathit{x}}_n\right)}{F^{\prime }\left({\mathit{x}}_n\right)}.$$

(24)

3.2. Initial Value of the Inverse Kinematics Solution

The motion ranges of each joint in the Da Vinci slave manipulator are as follows: θ₁ from −90° to 90°, θ₂ from −135° to 0°, l_IH from 0 to 315 mm, θ₃ from −180° to 180°, θ₄ from −90° to 90°, and θ₅ from −90° to 90°. In the previously defined x₁ = cos(q₁) + isin(q₁), q₁ is the rotation angle of the first joint with a range of [−π/2, π/2]. A finite number of values are obtained by extracting values within these available ranges at a certain angle interval (our subsequent calculation results show that a less than $5^{°}$ angle interval is acceptable) to solve the forward kinematics, the results of which are stored as the initial value database for the inverse kinematics solution. By selecting the data from the initial value database that is the least squares approximate to the required inverse kinematics as the initial values, the Newton iteration method will successfully converge.

3.3. Inverse Kinematics Solution Process

According to the inverse kinematics of the Da Vinci slave manipulator and the derived solution process, a detailed solution flow chart is constructed in Figure 3.

In Figure 3, T_end is the pose matrix at the endpoint of the robot (i.e., ⁰₆T), ε is the precision of the solution, θ₀ is the initial value, h is the initial step value, and X_s represents the values of each joint at previous positions. The value k is used to determine whether both forms of F(x₁) have been solved.

4. Example Analysis and Discussion

4.1. Parameters of the Da Vinci Slave Manipulator

According to Figure 4, the size parameters of the Da Vinci slave manipulator are shown in

Table 1. Structure parameters of the Da Vinci slave manipulator.

β1 (°)	β2 (°)	lQH (mm)	β3 (°)	α (°)	lIJ (mm)
30.45	7	784.29	0	20	10

.

4.2. Solution of Proposed Method

As shown in

Table 2. Inverse kinematics solution of the Da Vinci slave manipulator.

	Step (°)	Output h = 20	Error	Input		Step (°)	Output h = 20	Error	Input
Joint					Joint
θ1 (°)		10.00000000000004	0.00000000000004	10	θ1 (°)		15.39999999999996	0.00000000000003	15.4
θ2 (°)		−124.999999995	0.000000005	−125	θ2 (°)		−116.499999995	0.000000005	−116.5
lIH (mm)		100.0000000000001	0.0000000000001	100	lIH (mm)		101.3000000000001	0.0000000000001	101.3
θ3 (°)		99.999999995	0.000000005	100	θ3 (°)		86.3999999999996	0.0000000000004	86.4
θ4 (°)		−14.0000000000008	0.0000000000008	−14	θ4 (°)		13.6999999999998	0.0000000000002	13.7
θ5 (°)		18.000000002	0.000000002	18	θ5 (°)		−15.899999996	0.000000004	−15.9
t (s)		0.421			t (s)		0.406
	Step (°)	Output h = 10	Error	Input		Step (°)	Output h = 20	Error	Input
Joint					Joint
θ1 (°)		−50.240000000000009	0.000000000000009	−50.24	θ1 (°)		48.3689999999998	0.0000000000002	48.369
θ2 (°)		−60.759999999999998	0.000000000000002	−60.76	θ2 (°)		−80.59700000000002	0.00000000000002	−80.597
lIH (mm)		126.94000000000001	0.00000000000001	126.94	lIH (mm)		125.4680000000002	0.0000000000002	125.468
θ3 (°)		101.379999995	0.000000005	101.38	θ3 (°)		−80.593999999998	0.000000000002	−80.594
θ4 (°)		−15.9400000000002	0.0000000000002	−15.94	θ4 (°)		−68.5920000000003	0.0000000000003	−68.592
θ5 (°)		24.78999999	0.00000001	24.79	θ5 (°)		15.237999998966513		15.238
t (s)		0.484			t (s)		0.390
	Step (°)	Output h = 20	Error	Input		Step (°)	Output h = 20	Error	Input
Joint					Joint
θ1 (°)		−56.54835000000004	0.00000000000004	−56.54835	θ1 (°)		43.36587495200008	0.00000000000008	43.365874952
θ2 (°)		−53.89575999999999	0.00000000000001	−53.89576	θ2 (°)		−125.687459795	0.000000005	−125.6874598
lIH (mm)		168.85324	0.00004	168.8532	lIH (mm)		136.8452159699998	0.0000000000002	136.84521597
θ3 (°)		−96.358469995	0.000000005	−96.35847	θ3 (°)		75.312548960004	0.000000000004	75.31254896
θ4 (°)		−50.268430000001	0.000000000001	−50.26843	θ4 (°)		25.984572680002	0.000000000002	25.98457268
θ5 (°)		50.468509999	0.000000001	50.46851	θ5 (°)		−42.58794151	0.00000001	−42.587941523
t (s)		0.437			t (s)		0.437

(the form is referenced by the book: An Introduction to Error Analysis [27]), the input values are a set of arbitrarily selected joint parameters within the effective range of joint space. The outputs in Table 2 are the calculated values by our proposed method. h represents the step size of the solution, and the error is calculated as follows:

$$\mathsf{\epsilon }=\left|\mathrm{Output}-\mathrm{Input}\right|.$$

(25)

In this paper, the solution precision of the Newton–Raphson method is 1E–10 ε = 1E-7 for T_end, θ₀ takes the minimum value of −90° within the feasible region, and the initial step size is h₀ = 20°. The test carried on CodeBlocks 16.01 based on the hardware that a PC platform running with an Intel (R) Core (TM) i5-4460 CPU, clocked at 3.2 GHz (memory: 4 GB).

We also use the same input to run the procedure on the “R12CCPU-V” MELSEC iQ-R series C language controller from Mitsubishi Electric and VxWorks 6.9 operating system, the results are list in

Table 3. Inverse kinematics solution of the Da Vinci slave manipulator (based on better hardware and software).

	Step (°)	Output h = 20	Error	Input		Step (°)	Output h = 20	Error	Input
Joint					Joint
θ1 (°)		9.999999999999998	0.000000000000002	10	θ1 (°)		15.39999999999995	0.00000000000005	15.4
θ2 (°)		−124.999999995	0.000000005	−125	θ2 (°)		−116.499999995	0.000000005	−116.5
lIH (mm)		99.9999999999999	0.0000000000001	100	lIH (mm)		101.3000000000002	0.0000000000002	101.3
θ3 (°)		99.999999995	0.000000005	100	θ3 (°)		86.3999999999998	0.0000000000002	86.4
θ4 (°)		−13.9999999999995	0.0000000000005	−14	θ4 (°)		13.69999999999991	0.00000000000009	13.7
θ5 (°)		18.000000002	0.000000002	18	θ5 (°)		−15.899999996	0.000000004	−15.9
t (s)		0.016			t (s)		0.016
	Step (°)	Output h = 10	Error	Input		Step (°)	Output h = 20	Error	Input
Joint					Joint
θ1 (°)		−50.240000000000002	0.000000000000002	−50.24	θ1 (°)		48.3689999999998	0.0000000000002	48.369
θ2 (°)		−60.759999999999998	0.000000000000002	−60.76	θ2 (°)		−80.59699999999998	0.00000000000002	−80.597
lIH (mm)		126.9400000000001	0.0000000000001	126.94	lIH (mm)		125.4680000000002	0.0000000000002	125.468
θ3 (°)		101.379999995	0.000000005	101.38	θ3 (°)		−80.593999999998	0.0000000000002	−80.594
θ4 (°)		−15.9400000000008	0.0000000000008	−15.94	θ4 (°)		−68.5920000000003	0.0000000000003	−68.592
θ5 (°)		24.78999999	0.00000001	24.79	θ5 (°)		15.237999999	0.000000001	15.238
t (s)		0.016			t (s)		0.016
	Step (°)	Output h = 20	Error	Input		Step (°)	Output h = 20	Error	Input
Joint					Joint
θ1 (°)		−56.54835000000004	0.00000000000004	−56.54835	θ1 (°)		43.36587495200008	0.00000000000008	43.365874952
θ2 (°)		−53.89575999999999	0.00000000000001	−53.89576	θ2 (°)		−125.687459795	0.000000005	−125.6874598
lIH (mm)		168.85320000000007	0.00000000000007	168.8532	lIH (mm)		136.8452159699999	0.0000000000001	136.84521597
θ3 (°)		−96.358469995	0.000000005	−96.35847	θ3 (°)		75.3125489599998	0.0000000000002	75.31254896
θ4 (°)		−50.268430000001	0.000000000001	−50.26843	θ4 (°)		25.9845726799996	0.0000000000004	25.98457268
θ5 (°)		50.468509999	0.000000001	50.46851	θ5 (°)		−42.58794151	0.00000001	−42.587941523
t (s)		0.016			t (s)		0.016

.

In order to verify the proposed method, we build a simulation model in Adams. Firstly, we gave a random movement for the simulation model, then we obtained the matrix of the end pose from the simulation result (Figure 5a), which included the position and the orientation. Secondly, the matrixes were imported to the algorithm we proposed as input. Thirdly, we used our solution to drive the robot model. In the final results, depicted in Figure 5b, we see that the curve obtained by our algorithm is very close to the target curve. This means the proposed method is of high accuracy.

4.3. Discussion of the Solution

As noted in the previous section, the main focus of the solution includes the solution accuracy, real-time performance (solution speed) and the singularity problem (based on the joint position solution or not).

(1) Solution accuracy

Table 2 shows that for any input joint parameter, whether an integer or a decimal value accurate to nine decimal places, the error between the calculated values (output) and the given values (input) of six joint parameters of the slave manipulator is within 0.00004 degree (or mm), which demonstrates that the proposed approach for the Da Vinci surgical robot inverse kinematics is capable of finding effective solutions with high accuracy.

(2) Solution speed

The number of calculation steps of the algorithm/program is one of the influential factors that affect the solution speed. As schematically shown in Figure 3, the number of steps of the inverse kinematics approach proposed in this paper depends mainly on two factors:

① The number of Newton iterations in the best-case scenario, the numerical solution can be obtained by one iteration when the initial value is perfectly selected. In general, if the given initial value ensures convergence, then the solution of F(x₁) = 0 is expected to take approximate 20 iterations; in cases where the convergence fails, the program is designed to iterate at most 50 times and then exit to avoid a dead loop.

② The step size. when the step size h is large, the iteration times are reduced, thereby shorten the calculation time. However, the selection of initial values will be relatively imprecise, resulting in higher possibility of solution failure due to unreasonable initial values. In cases where the step size is small, the initial values tend to be more precise, resulting in a greater possibility of obtaining a solution. However, the resulting shortcoming is the demand for more calculation steps and longer time.

An improved calculation process is proposed by taking both factors into account: first, start the procedure by following the flow chart shown in Figure 3 with a relatively large step size; second, reduce the step size gradually for more precise initial values if the equation has no solution. This approach boosts the speed of calculation but also reduces the possibility of solution failure.

(3) Singularity influences

Our method abandons the use of Jacobian matrix inversion. Therefore, there will be barely no singular solution in the condition of a good initial value from a mathematical perspective. On the other hand, because our algorithm is based on the position increment of the manipulator’s joints, Then, the motion joint position trajectory is generated by interpolation based on the initial joint position and the end joint position. The joint position interpolation is not affected by the singularity.

4.4. Comparison with Other Methods

Table 4. Comparison between the proposed method and others.

Method	Applicability	Complexity of Calculation	Solution Precision	Solution Speed	Singularity Influences
separates the position and orientation [10,11]	especially for the structure satisfied Pieper principle	low	high	quick	need to consider about
method based on the Jacobian matrix [16,28]	all	high	middle	not quick	need to consider about
The proposed method	especially for the structure not satisfied Pieper principle	middle	high	quick	barely considering about

compared our method with another two typical methods in applicability, complexity of calculation, solution precision, solution speed and singularity influences.

Particularly, we choose separates the position and orientation method (name as “separate P&R method” below) to applied on the Da Vinci slave manipulator, and the comparison with the proposed method within the same simulation model is shown in Figure 6. The position curve of “separate P&R method” is following the target with some fluctuation, while the orientation result is far away from the correct solution, which means that the Separate P&R method is not suitable for the slave manipulator that dissatisfied the Pieper principle. Even though increasing the error feedback to compensate for the results may increase the solution precision, the compensation operation will take a large amount of time, which proves the superiority of our proposed method in terms of solution precision and speed.

5. Conclusions

(1) In this paper, an inverse kinematics mathematical model of the 6-DOF active arm of the Da Vinci surgical robot established by using a coordinate transformation matrix method according to its mechanical motion diagram and working characteristics. By introducing a unitary matrix, the mathematical model on the real plane is transformed to a complex plane, consequently avoiding the relatively complex trigonometric calculations associated with the conventional solution procedure. Following the steps proposed, this approach can apply to other similar robot kinematic problems.

(2) The dialytic elimination method serves to individually eliminate the joint variables and ultimately obtains a high-order nonlinear equation with only one unknown variable of the first joint. Subsequently, the Newton iteration method is introduced to solve the nonlinear equation on the basis of selecting multiple initial values reasonably in the feasible region. The test shows that carefully changing the step size and selecting initial values in the feasible region for the iteration solution of the nonlinear equation will significantly reduce the possibility of solution failure.

(3) In theory, the accuracy of the approach can reach an error of < 0.00004 degree (or mm) and achieve a solution time of 0.5 s (Intel (R) Core i5-4460 CPU, clocked at 3.2 GHz (memory: 4 GB)). Running the procedure on better hardware and software (based on the “R12CCPU-V” MELSEC iQ-R series C language controller from Mitsubishi Electric and VxWorks 6.9 operating system) decreases the solution time to 20 ms, which fully satisfies the real-time performance requirement of surgical robots.

(4) A method that combines dialytic elimination and the Newton iteration method is applied to solve the inverse kinematics problem of the slave manipulators of the master–slave surgical robot. The proposed approach achieves higher accuracy than other solutions based on position and orientation separation while the real-time performance is satisfied. Moreover, in contrast to other numerical solutions, the solution method is based on the position of the joint and is therefore barely not affected by any singularity. Further, the application of our approach removes the restriction of the design of the master manipulator configuration.