Numerical Analysis of a Catenary Mooring System Attached by Clump Masses for Improving the Wave-Resistance Ability of a Spar Buoy-Type Floating Offshore Wind Turbine
Abstract
:1. Introduction
2. Numerical Theories
2.1. Blade Element Momentum Theory
2.2. Quasi-Static and Multi-Segment Theory
2.3. Potential Flow Theory
2.4. Equations of Motion
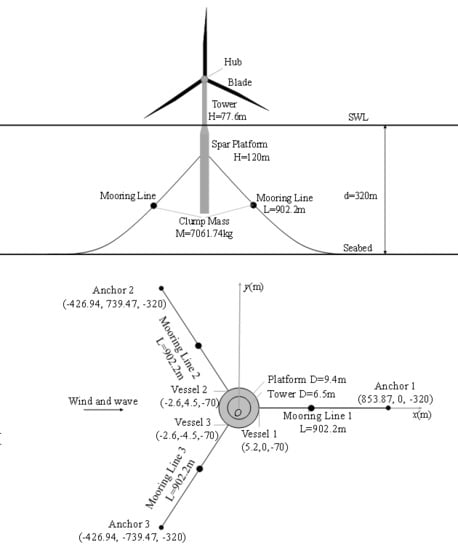
3. Configurations of OC3CM Model
3.1. OC3CM Models
3.2. Load Cases
4. Results and Discussions
4.1. Validation of the Code
4.2. Regular Waves
4.3. Irregular Waves
4.4. Fairlead Tension
5. Conclusions
- Through the comparison of the free decay test, it can be concluded that the code developed in-house is accurate, so it can be used for subsequent research on OC3 offshore wind turbines.
- The OC3CM model can significantly reduce the surge of the spar platform at wind and wave loads, and the clump masses are more effective when they are mounted closer to the sea bed. However, it must be pointed out that the clump masses cannot be located too close to the anchor point, otherwise they will make the connection node touch the seabed. The best model is the OC3CM model P5, which can reduce the value of the surge by about 30.89% under a regular wave and reduce the peak amplitude of surge by about 38.4% under an irregular wave.
- The OC3CM model has no significant effect on the heave of the spar platform under wind and regular wave loads; however, after adding the clump masses, the platform will settle about 1.3 m, but the impact is negligible compared to its draught depth of 120 m. In addition, the OC3CM model P5 induces a small change in the peak pitch amplitude, while the OC3CM model P5 can reduce the peak pitch amplitude and the peak heave amplitude by about 20% and 19%, respectively, in the wind and irregular wave load.
- The clump masses will increase the fairlead 1 tension by about 30% and increase the fairlead 2 and 3 tensions by about 24.5%. However, the position of the clump masses and the changes of wind and wave loads indicate no significant effect on the fairlead tension. The segment of the mooring line from the connection node to the vessel node is obviously straightened by the clump masses. This will increase the tension of the mooring line and should, therefore, limit the motion of the platform. The affected frequency range makes a difference to the fatigue loads on the moorings, but the regularity is not obvious. At the same time, the fatigue loads of the OC3CM model P5 and P2 are relatively small.
- This paper only intends to provide a way to reduce the response motions, regardless of its increased cost. In subsequent studies, the cost will be taken into consideration and the platform structure as well as the mooring system will be changed simultaneously. These changes are expected to make the OC3-Hywind have better performance under different environmental conditions and better economic benefits.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Axial induction factor |
| Tangential induction factor | |
| Linear acceleration of the structure () | |
| Added-mass due to radiation at the reference point | |
| B | Number of the blades |
| Leaf chord length (m) | |
| Hydrostatic-restoring matrix | |
| Coefficients for the normal force | |
| Coefficients for the thrust force | |
| EA | Cross section axial stiffness (kN) |
| Total added mass forces from all contributions (kN) | |
| Hydrostatic forces at the reference node (kN) | |
| Mooring tension (kN) | |
| Radiation memory-effect force at the reference point (kN) | |
| Incident-wave excitation force at reference point (kN) | |
| Total loads at the reference point (kN) | |
| Wind loads applied to the blades and tower (kN) | |
| Applied horizontal and vertical force at the fairlead, respectively (kN) | |
| g | Acceleration due to gravity () |
| K | Hydrostatic restoring force matrix |
| Radiation kernel from potential flow theory | |
| L | Upstretched line length (m) |
| Wave spectrum (P-M spectrum in this paper) | |
| t | Time (s) |
| Volume of the immersed part of the platform (m3) | |
| Wind speed () | |
| Fourier transform of a white noise time series with unit variance | |
| ω | Frequency (Hz) |
| x | Platform motions (m) |
| Platform velocity () | |
| , | Cable profile in the horizontal planes at distance s along the line (m) |
| Cable profile in the vertical planes at distance s along the line (m) | |
| Wave-induced force array normalized per unit wave amplitude () | |
| Component of the Kronecker‒Delta function | |
| β | Incident wave direction angle (degree) |
| AQWA | Integrated Module Under ANSYS |
| CAES | Compressed Air Energy Storage |
| DOF | Degree of Freedom |
| FAST | Fatigue, Aerodynamics, Structures, and Turbulence |
| FOWT | Floating Offshore Wind Turbine |
| IEA | The International Energy Agency |
| CM | Clump masses |
| MSQS | Multi-Segmented, Quasi-Static |
| NREL | National Renewable Energy Laboratory |
| OC3 | Offshore Code Comparison Collaboration |
| OC4 | Offshore Code Comparison Collaboration Continuation |
| P-M | Pierson and Moskowitz |
| RAO | Response Amplitude Operator |
| RNA | Rotor Nacelle Assembly |
| SFFC | Steel Fish-Farming Cage |
| SWL | Still Water Level |
| TLP | Tension Leg Platform |
References
- Madjid, K.; Torgeir, M. Feasibility of the Application of a Spar-type Wind Turbine at a Moderate Water Depth. Energy Procedia 2012, 24, 340–350. [Google Scholar] [Green Version]
- Hao, K.J.; Robertson, A.N.; Jonkman, J.; Driscoll, F.; Ng, E.Y.K. Building and Calibration of a Fast Model of the Sway Prototype Floating Wind Turbine. In Proceedings of the International Conference on Renewable Energy Research and Applications (ICRERA), Madrid, Spain, 20–23 October 2013. [Google Scholar]
- Sethuraman, L.; Venugopal, V. Hydrodynamic response of a stepped-spar floating wind turbine: Numerical modelling and tank testing. Renew. Energy 2013, 52, 160–174. [Google Scholar] [CrossRef]
- Utsunomiya, T.; Sato, T.; Matsukuma, H.; Yago, K. Experimental validation for motion of a spar-type floating offshore wind turbine using 1/22.5 scale model. In Proceedings of the ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, Osaka, Japan, 21–26 July 2009; pp. 951–959. [Google Scholar]
- Utsunomiya, T.; Nishida, E.; Sato, I. Wave response experiment on spar-type floating bodies for offshore wind turbine. In Proceedings of the 19th International Offshore and Polar Engineering Conference, Osaka, Japan, 21–26 July 2009. [Google Scholar]
- Roddier, D.C.; Cermelli, A.A.; Weinstein, A. WindFloat: A floating foundation for offshore wind turbines. J. Renew. Sustain. Energy 2010, 2. [Google Scholar] [CrossRef]
- Duan, F.; Hu, Z.Q.; Wang, J. Investigation of the VIMs of a spar-type FOWT using a model test method. J. Renew. Sustain. Energy 2016, 8. [Google Scholar] [CrossRef]
- Adam, F.; Myland, T.; Schuldt, B.; Großmann, J.; Dahlhaus, F. Evaluation of internal force superposition on a TLP for wind turbines. Renew. Energy 2014, 71, 271–275. [Google Scholar] [CrossRef]
- Vita, L.; Ramachandran, G.K.V.; Krieger, A.; Kvittem, M.I.; Merino, D.; Cross-Whiter, J.; Ackers, B.B. Comparison of Numerical Models and Verification Against Experimental Data, Using PelaStar TLP Concept. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar]
- Bulder, B.H.; Van, H.; Henderson, A.; Huijsmans, R.H.M.; Pierik, J.T.G.; Snijders, E.J.B.; Wijnants, G.H.; Wolf, M.J. Studie Naar Haalbaarheid van en Randvoorwaarden Voor Drijvende Offshore Windturbines; Drijfwind Project Report; TNO: Delft, The Netherlands, 2002. [Google Scholar]
- Karimirad, M.; Michailides, C. V-shaped semisubmersible offshore wind turbine: An alternative concept for offshore wind technology. Renew. Energy 2015, 83, 126–143. [Google Scholar]
- Paulsen, U.S.; Borg, M.; Madsen, H.A. Outcomes of the DeepWind conceptual design. Energy Procedia 2015, 80, 329–341. [Google Scholar]
- Bedon, G.; Paulsen, U.S.; Madsen, H.A.; Belloni, F.; Castelli, M.; Benini, E. Aerodynamic Benchmarking of the Deepwind Design. Energy Procedia 2015, 75, 677–682. [Google Scholar] [CrossRef] [Green Version]
- Beyer, F.; Choisnet, T.; Kretschmer, M.; Cheng, P.W. Coupled MBS-CFD Simulation of the Ideol Floating Offshore Wind Turbine Foundation Compared to Wave Tank Model Test Data. In Proceedings of the 25th (2015) International Ocean and Polar Engineering Conference, Kona (Big Island), HI, USA, 21–26 June 2015. [Google Scholar]
- Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semisubmersible Floating System for Phase II of OC4; NREL/TP-5000-60601; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2014. [Google Scholar]
- Ai, N.; David, J.O.; Gretar, T. Nonlinear simulation of a spar buoy floating wind turbine under extreme ocean conditions. J. Renew. Sustain. Energy 2014, 6. [Google Scholar] [CrossRef]
- Chen, J.H.; Hu, Z.Q.; Duan, F. Comparisons of dynamical characteristics of a 5 MW floating wind turbine supported by a spar-buoy and a semi-submersible using model testing methods. J. Renew. Sustain. Energy 2018, 10. [Google Scholar] [CrossRef]
- Karimirad, M.; Gao, Z.; Moan, T. Dynamic Motion Analysis of Catenary Moored Spar Wind Turbine in Extreme Environmental Condition. In Proceedings of the European Offshore Wind 2009 Conference, Stockholm, Sweden, 14–16 September 2009. [Google Scholar]
- Driscoll, F.; Jonkman, J.; Robertson, A.; Sirnivas, S.; Skaare, B.; Nielsen, F.G. Validation of a fast model of the statoil-hywind demo floating wind turbine. Energy Procedia 2016, 94, 3–19. [Google Scholar] [CrossRef]
- Mahmudur, R.S.; Saiful, I.; Mohd, Z.J.; Zainah, I.; Rafiqul, M.I.; Nazmul, H. Hydrodynamic response of floating coupled spar in deep sea. In Proceedings of the 10th International Conference on Marine Technology (MARTEC 2016), Dhaka, Bangladesh, 9–10 December 2016. [Google Scholar]
- Shen, W.J. Numerical wind-tunnel simulation for Spar platform. AIP Conf. Proc. 2017, 1839. [Google Scholar] [CrossRef]
- Myhr, A.; Maus, K.J.; Nygaard, T.A. Experimental and computational comparisons of the OC3-hywind and tension-leg-buoy (TLB) floating wind turbine conceptual designs. In Proceedings of the 21st International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Nielsen, F.G.; Hanson, T.D.; Skaare, B. Integrated dynamic analysis of floating offshore wind turbines. In Proceedings of the ASME 2006 25th International Conference on Ocean, Offshore and Arctic Engineering, Hamburg, Germany, 4–9 June 2006; pp. 671–679. [Google Scholar]
- Jonkman, J.; Musial, W. Offshore Code Comparison Collaboration (OC3) for IEA Wind Task 23 Offshore Wind Technology and Deployment; NREL/TP-5000-48191; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2010. [Google Scholar]
- Shin, H. Model Test of the OC3-Hywind Floating Offshore Wind Turbine. In Proceedings of the 21st International Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011. [Google Scholar]
- Ye, Z.; Zhou, W.; Zhang, P.; Li, C. Research on Structural Optimization Design of Spar Platform for Offshore Wind Turbine. J. Water Resour. Water Eng. 2018, 29, 156–162. [Google Scholar]
- Li, F.; You, Y.X.; Chen, K. Investigation on the Load Characteristics of Spar Platform with Spiral Strakes under Internal Solitary Waves. Chin. J. Hydrodyn. 2018, 33, 470–479. [Google Scholar]
- Zhang, H.H.; Zhang, H.X.; Yao, H.L. Numerical Simulation on the Hydrodynamics Forces of Spar Platform with Heave Plate. Chin. J. Hydrodyn. 2018, 33, 150–161. [Google Scholar]
- Wang, Y.Z.; Xu, X.P.; Liu, G.D. Analysis of Effect of Heave Plate on Vertical Motion Performance of Truss Spar Platform. China Pet. Mach. 2017, 45, 46–50. [Google Scholar]
- Chen, D.; Gao, P.; Huang, S.S.; Fan, K.; Zhuang, N.; Liao, Y.D. Dynamic response and mooring optimization of spar-type substructure under combined action of wind, wave, and current. J. Renew. Sustain. Energy 2017, 9. [Google Scholar] [CrossRef]
- Hyunkyoung, S.; Wooseob, L.; Kwangjin, J.; Jungtae, K. Model test and simulation of modified spar type floating offshore wind turbine with three catenary mooring lines. J. Renew. Sustain. Energy 2014, 6. [Google Scholar] [CrossRef]
- Zheng, X.Y.; Lei, Y. Stochastic Response Analysis for a Floating Offshore Wind Turbine Integrated with a Steel Fish Farming Cage. Appl. Sci. 2018, 8, 1229. [Google Scholar] [CrossRef]
- Yu, W.; Ding, Q.; Li, C.; Hao, W.X.; Zhou, H.J.; Zhang, K. Influence of Heave Plate on the Dynamic Response of a Floating Wind Turbine Platform. J. Chin. Soc. Power Eng. 2018, 38, 747–754. [Google Scholar]
- Li, A.J.; Tang, B.Y.; Yeung, C.R. Effects of second-order difference-frequency wave forces on a new floating platform for an offshore wind turbine. J. Renew. Sustain. Energy 2014, 6. [Google Scholar] [CrossRef]
- Yuan, Z.M.; Atilla, I.; Ji, C.Y. Numerical study on a hybrid mooring system with clump weights and buoys. Ocean. Eng. 2014, 88, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Tore, H. Design Analysis and Optimisation of Mooring System for Floating wind Turbines. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2014. [Google Scholar]
- Jonkman, J.M.; Hayman, G.J.; Jonlman, B.J.; Damiani, R.R.; Murray, R.E. AeroDyn v15 User’s Guide and Theory Manual; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2016. [Google Scholar]
- Jonkman, J.M.; Robertson, A.N.; Hayman, G.J. HydroDyn User’s Guide and Theory Manual; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2015. [Google Scholar]
- Jonkman, J. Definition of the Floating System for Phase IV of OC3; NREL/TP-500-47535; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2010. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; NREL/TP-500-38060; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Masciola, M.; Jonkman, J.; Robertson, A.N. Implementation of a Multisegmented, Quasi-Static Cable Model. In Proceedings of the 23th International Ocean (Offshore) and Polar Engineering Conference, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
- Jonkman, J. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine; NREL/TP-500-41958; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2007. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1973; ISBN 0-521-09817-3. [Google Scholar]
- Wang, H.; Hu, Z.Q.; Meng, X.Y. Dynamic Performance Investigation of A Spar-Type Floating Wind Turbine Under Different Sea Conditions. China Ocean. Eng. 2018, 32, 256–265. [Google Scholar] [CrossRef]
- Si, Y.L.; Karimi, H.R.; Gao, H.J. Modeling and Parameter Analysis of the OC3-Hywind Floating Wind Turbine with a Tuned Mass Damper in Nacelle. J. Appl. Math. 2013, 2013, 679071. [Google Scholar] [CrossRef]




















| Research | Hydrodynamic Theory | Platform | Design | Fatigue Load | Focus | Optimized Parameter |
|---|---|---|---|---|---|---|
| Present study | Potential flow theory | Spar |  | Yes | Optimized position of the clump masses | Motions of platform |
| Yuan’s study [30] | Morison’s Equation | Semi-submersible |  | No | Optimized position and volume of the buoys | Tension of mooring line |
| Tore’s study [31] | Generalized Morison’s Equation | Spar |  | No | Optimized size and position of the clump masses | Tension of mooring line |
| Item | Value |
|---|---|
| Rating | 5 MW |
| Rotor type | Upwind, 3 blades |
| Total draft below sea water level (SWL) | 120 m |
| Tower base above SWL | 10 m |
| Hub height above SWL | 90 m |
| Nacelle dimension (length, width, height) | 14.2 m, 2.3 m, 3.5 m |
| Platform diameter above taper | 6.5 m |
| Platform diameter below taper | 9.4 m |
| Rotor nacelle assembly (RNA) mass | 350,000 kg |
| Tower mass | 249,718 kg |
| Platform mass | 7,466,330 kg |
| Hub mass | 56,780 kg |
| Number of mooring lines | 3 |
| Depth to fairleads below SWL | 70 |
| Global coordinates of the anchor point 1 | (853.87 m, 0, −320 m) |
| Global coordinates of the fairlead point 1 | (5.2 m, 0, −70 m) |
| Mooring line diameter | 0.09 m |
| Mooring line mass density | 77.71 kg m−1 |
| Model | LM | mCM |
|---|---|---|
| P0 | 0 | 0 |
| P1 | 0.7L | 7061.74 kg |
| P2 | 0.6L | 7061.74 kg |
| P3 | 0.5L | 7061.74 kg |
| P4 | 0.4L | 7061.74 kg |
| P5 | 0.3L | 7061.74 kg |
| Load Cases | H or Hs (m) | T or Tp (s) | Wind Speed (m/s) | Wave |
|---|---|---|---|---|
| Case 1 | 6 | 10 | 8 | Regular wave (Airy) |
| Case 2 | 2.56 | 7 | 8 | Regular wave (Airy) |
| Case 3 | 4 | 8 | 8 | Regular wave (Airy) |
| Case 4 | 6.7 | 8.6 | 8 | Irregular wave (P‒M) |
| Case 5 | 3.66 | 9.7 | 8 | Irregular wave (P‒M) |
| Case 6 | 9.14 | 13.6 | 8 | Irregular wave (P‒M) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Tu, Y.; Wang, W.; Qian, G. Numerical Analysis of a Catenary Mooring System Attached by Clump Masses for Improving the Wave-Resistance Ability of a Spar Buoy-Type Floating Offshore Wind Turbine. Appl. Sci. 2019, 9, 1075. https://doi.org/10.3390/app9061075
Liu Z, Tu Y, Wang W, Qian G. Numerical Analysis of a Catenary Mooring System Attached by Clump Masses for Improving the Wave-Resistance Ability of a Spar Buoy-Type Floating Offshore Wind Turbine. Applied Sciences. 2019; 9(6):1075. https://doi.org/10.3390/app9061075
Chicago/Turabian StyleLiu, Zhenqing, Yuangang Tu, Wei Wang, and Guowei Qian. 2019. "Numerical Analysis of a Catenary Mooring System Attached by Clump Masses for Improving the Wave-Resistance Ability of a Spar Buoy-Type Floating Offshore Wind Turbine" Applied Sciences 9, no. 6: 1075. https://doi.org/10.3390/app9061075
APA StyleLiu, Z., Tu, Y., Wang, W., & Qian, G. (2019). Numerical Analysis of a Catenary Mooring System Attached by Clump Masses for Improving the Wave-Resistance Ability of a Spar Buoy-Type Floating Offshore Wind Turbine. Applied Sciences, 9(6), 1075. https://doi.org/10.3390/app9061075